Cash Flow Calculations

This chapter discusses cash flow calculation concepts and processes.

This chapter covers the following topics:

• Overview of Cash Flow Calculations
• Cash Flow Calculations Characteristics and Concepts
• The Cash Flow Calculation Process
• Detail Cash Flow Data
• Financial Element Calculations
• Example of the Rule of 78

Overview of Cash Flow Calculations

Oracle Transfer Pricing makes use of the OFS Cash Flow Engine to ensure modeling consistency across Oracle Financial Services (OFS) applications. An understanding of the Oracle Transfer Pricing cash flow calculations requires knowledge of cash flow calculation concepts and processes as well as that of the capabilities of the OFS Cash Flow Engine and the calculations that can be performed by it.

Note: As cash flows for an instrument are modeled through time, the data associated with the instrument changes due to payments, repricings, and other characteristics or events. These changes apply only in memory and do not affect the information stored in the Account Tables.

In this exposition, a subscript notation of m for memory and r for detail record helps differentiate between forecasted and actual data. For example, Current paymentr refers to the current payment stored in the Account Table. Current paymentm refers to the current payment in memory that is updated each time a payment recalculation occurs.

Cash Flow Calculations Characteristics and Concepts

A complete understanding of Oracle Transfer Pricing cash flow calculations requires familiarity with the following key concepts and characteristics:

• Instrument Level Modeling

• Modeling Flexibility

• Daily Cash Flows

• Event-Driven Logic

• Financial Elements

Related Topics

Overview of Cash Flow Calculations

Instrument Level Modeling

Several transfer pricing methods require cash flows to generate results. Oracle Transfer Pricing supports the following cash flow transfer pricing methods:

• Duration

• Weighted Average Cash Flow

• Zero Coupon Pricing

Oracle Transfer Pricing generates cash flows at the individual instrument level. Each individual instrument record processed generates a set of cash flows as defined by that instrument record's product characteristics. The cash flows produced are then processed further to generate the required results such as transfer rates or option costs.

The usage of cash flows generated from individual instruments for processing provides an optimum level of accuracy.

Related Topics

Cash Flow Calculations Characteristics and Concepts

Modeling Flexibility

Oracle Transfer Pricing instrument data provides for modeling flexibility. Each instrument record has the following data:

• Payment information (dates, frequencies, and amounts)

• Balance information (current and original balance)

• Rate information (gross, net, and transfer rate)

Specific cash flow characteristics defined in an instrument record determine the cash flows to be generated. There are more than 50 data columns that directly affect the cash flow results. Depending on the information in these columns, you can model an unlimited number of instruments.

Related Topics

Cash Flow Calculations Characteristics and Concepts

Daily Cash Flows

Oracle Transfer Pricing lets you set instrument records in such a manner that cash flows can occur on any date, and with any frequency thereafter. This functionality is essential for generating accurate results.

Related Topics

Cash Flow Calculations Characteristics and Concepts

Event-Driven Logic

Oracle Transfer Pricing generates cash flows as a series of events. On any day, and with any frequency, depending on the instrument characteristics, any of the following events can occur:

• Payment

• Repricing

• Payment recalculation

• Prepayment

Each of these events requires cash flow calculations.

Related Topics

Cash Flow Calculations Characteristics and Concepts

Financial Elements

On an event date, such as a payment or repricing event date, the OFS Cash Flow Engine computes the results of that event. The results of an event are represented in the form of financial elements. For example, on a payment event date, the Cash Flow Engine can compute the following:

• Interest

• Principal runoff

• Total cash flow

• Ending balance

The cash flow engine generates and outputs over 50 financial elements to the FTP_PROCESS_CASH_FLOWS table that can be used to validate results.

Related Topics

Cash Flow Calculations Characteristics and Concepts

The Cash Flow Calculation Process

The cash flow calculation process comprises the following broad stages:

1. Initialization of the modeling data and parameters for the instruments to be modeled. See: Initialization of Modeling Data and Parameters.

2. Processing of modeling events until current date equals the maturity date or the modeling end date, or the current balance equals zero. This stage involves the following steps:

   • Calculation of changes to the underlying instruments

   • Calculation of financial elements associated with an event

   • Computation of the next event date

See: Processing Modeling Events.

Related Topics

Overview of Cash Flow Calculations

Initialization of Modeling Data and Parameters

The first step in the cash flow calculation process is to gather the information necessary to model an instrument. This information is available from several sources, including:

• Account tables

• Payment Schedule table

• Payment Pattern interface

• Reprice Pattern interface

• The rules specified in the Process rule

Related Topics

The Cash Flow Calculation Process

Determination of Account Type

The Extended Account Type attribute of the Line Item Dimension Member determines the account type of an individual record. Account types:

• Classify instruments based on their use in financial statements.

• Determine the cash flow processing types of the instruments: detail cash flow, balance only, or interest only.

The following table illustrates the different cash flow processing types and associated account types.

Cash Flow Processing Types

Cash Flow Types	Process Description - Detail	Associated Account Type
Detail cash flow	Processes daily cash flow events and generates necessary financial elements.	Interest-Earning Asset Interest-bearing Liability Off Balance Sheet Receivable Off Balance Sheet Payable
Balance Only	Processes the record originating on the origination date and running off on the maturity date. No payments are processed.	Other Asset Other Liability
Interest Only	Processes the instrument as a single interest payment covering the time from the origination date to the maturity date. Recognizes the current balance as an interest cash flow on the maturity date, but accrues interest from the origination date to the maturity date.	Interest Income Interest Expense

Note: For information about financial elements output by account types, see the Financial Element Calculations table.

Related Topics

Initialization of Modeling Data and Parameters

Initialization of Interface Data

Data retrieved from the interface impacts how an instrument is processed. The interface data that affect processing are as follows:

• User Defined Payment Patterns

• User Defined Repricing Patterns

User Defined Payment Patterns

Payment pattern data is retrieved when the cash flow engine needs to process an instrument that has a payment pattern code ranging from 1000 to 29999 as its amortization type code.

The amortization type code from the detail instrument record is matched to the set of payment pattern data with the same code. If no match is found for the amortization code from the detail record, the instrument record is assumed to be of nonamortizing type.

User Defined Repricing Pattern

Repricing pattern data is retrieved when the cash flow engine needs to process an instrument that has a repricing pattern code ranging from 500 to 998 as its adjustable type code.

If no related repricing pattern data is found, the engine defaults to the record characteristics in the repricing frequency column and processes the instrument as a standard adjustable instrument.

When a match is made, the instrument is modeled based on the repricing pattern. The cash flow engine first evaluates the status of the instrument as of the starting date of the cash flow process. The current repricing date is determined by rolling forward from the origination date to the next repricing date that follows the process start date. If the process start date does not correspond to the next repricing date, the repricing date from the record is used.

A repricing event is triggered when the period between two repricing events has elapsed. When this occurs, the defined rates are assigned to the detail record of the instrument. If the repricing type is Flat Rate, the rate from the event detail of the repricing pattern is applied to the detail record of the instrument. If the repricing type is Indexed Rate, a rate lookup is triggered for the customer rate and the transfer pricing rate. If the interest rate code (IRC) is a yield curve, the point on the yield curve used is the repricing term associated with the current repricing information, unless the IRC term has been specified in the repricing pattern event. This rate, plus the specified margin, is the new fully indexed rate. Rate caps and floors are applied after this calculation occurs.

Related Topics

Initialization of Modeling Data and Parameters

Initialization of Cash Flow Data

The cash flow engine gathers the cash flow data for the instrument to be processed. The cash flow data for an instrument is a subset of the information stored in the Account Tables for that instrument record. For a complete list of columns referenced in the cash flow calculation process, see theFinancial Element Calculations table.

The cash flow data provides current information about the characteristics of a cash flow instrument. This information must be consistent to ensure accurate output. Before processing cash flows, the cash flow edits checks should be run to avoid producing unreasonable results. See:

• Cash Flow Edits, Oracle Transfer Pricing User Guide.

• Overview of Cash Flow Edit Logic.

Cash flow data can be classified into the following three categories defining its use during the processing of an event:

• Static Characteristics

• Dynamic Characteristics

• Triggers

Static Characteristics

Static characteristics provide information to the cash flow engine about how the instrument should be modeled. For non-pattern and non-schedule instruments, all of the following characteristics remain constant during the modeling process:

• Event Frequencies:

  • Repricing

  • Payment

  • Payment Change

• Financial Code Values:

  • Accrual Basis Code

  • Amortization Type Code

  • Rate Change Round Code

• Dimensions:

  • Line Item Dimensions Members

  • Line Item Hierarchy

  • Currency Codes

• Repricing Parameters:

  • Margin

  • Rate Caps

  • Rate Increase Period

  • Rate Change Minimum

For pattern and schedule instruments, the payment frequency can vary throughout the life of the instrument.

Dynamic Characteristics

Dynamic characteristics are updated each time an event occurs, as a result of what has occurred during the event. These include the following:

• Balances:

  • Current

  • Current Deferred

• Rates:

  • Current Net

  • Current Gross

  • Current Transfer

• Event Counters (remaining number of payments)

Triggers

Triggers signal the cash flow engine when it is time to model a particular event and can change their value during the modeling process. These include the following:

• Event Dates:

  • Next Payment

  • Next Reprice

  • Payment Change

• Negative Amortization (NGAM or neg-am) Balance (in conjunction with neg-am limit)

Related Topics

Initialization of Modeling Data and Parameters

Initialization of Schedule Records

Oracle Transfer Pricing provides a payment schedule table, FTP_PAYMENT_SCHEDULE, for loading cash flow details related to instruments that have unique, non-standard payment characteristics which cannot easily be captured using traditional amortization methods or into a payment pattern definition. To properly model scheduled-amortization instruments, the cash flow engine must retrieve payment dates and payment amounts from the payment schedule table.

The payment schedule table is referenced by the Cash Flow engine by lookup, based on a match of the Instrument type code (INSTRUMENT_TYPE_CODE) and Account number (ID_NUMBER) columns from the instrument record to the same data in the payment schedule table. The Cash Flow engine looks at this table when the AMRT_TYPE_CODE column on the instrument record is populated with a value of 800, 801, or 802. If no match is found, the instrument is processed as a non-amortizing record.

Amortization Code 800

An amortization code of 800 denotes conventional payment schedule and signifies that payment amounts are principal and interest amounts. On payment dates, these payments are processed as conventional amortization payments.

Amortization Code 801

An amortization code of 801 denotes level principal payment schedules. On the schedules for these instruments, the payment amount comprises the principal portion of the payment only. For both conventional (800) and level principal (801) payment schedules, the payment amounts should be expressed gross of any participations.

Amortization Code 802

An amortization code of 802 denotes simple interest payment schedule. Instruments with amortization codes of 802 do not reference the principal amount column in the schedule tables. These instruments are processed as interest only records, with all principal, with the exception of prepayments, running off on the maturity date.

The data in the maturity date, next payment date, last payment date, remaining number of payments, and current payment columns of the instrument record should coincide with the same information in the schedule table. When this information is inconsistent, the information in the detail record supersedes the data in the schedule table.

In this case, the payment on the next payment date occurs on the date defined in the next payment date column of the instrument record, for the amount defined in the current payment column of the instrument record.

All payments after this date and before the maturity date are made according to the payment date in the schedule table. On the maturity date, the date from the maturity date column of the instrument record is used to pay off the remaining balance of the instrument record. If payment dates exist in the schedule beyond this date, they are ignored.

Related Topics

Initialization of Modeling Data and Parameters

Initialization of Pattern Records

The following logic applies to both user defined payment and repricing patterns.

Single Timeline Patterns

To initialize an instrument record whose payment (or repricing) characteristics are defined by a single timeline pattern, the cash flow engine must synchronize the detail instrument record with the payment (or repricing) pattern. Synchronization determines the current payment of the instrument within the payment (or repricing) pattern.

The synchronization process depends on whether the pattern is relative or absolute.

To synchronize a relative pattern, the cash flow engine calculates the payment (or repricing) dates for the instrument record by rolling the origination date forward by the pattern frequencies. Once it calculates a payment (or repricing) date greater than the calendar period end date, it stops. The number of times it was necessary to roll the date forward determines the current payment (or repricing event) number for the record.

Example

An instrument record processed on an calendar period end date of 03/31/1996 with an origination date of 01/01/1996, and a next payment (or repricing) date of 05/15/1996 is matched to the pattern described in the following table:

Example of Single Timeline Pattern

Row #	Frequency	Repetitions
1	1 M	3
2	3 M	3

The origination date is rolled forward in the following manner from the Starting point - 01/01/1996:

• Add first monthly payment (or repricing) frequency - 02/01/1996

• Add second monthly payment (or repricing) frequency - 03/01/1996

• Add third monthly payment (or repricing) frequency - 04/01/1996

After the third roll forward, the payment (or repricing) date is greater than the calendar period end date. The cash flow engine interprets that the record is on its third payment (or repricing), which is the final monthly payment (or repricing). It models this payment (or repricing) on the next payment (or repricing) date from the detail record, in this case, 05/15/1996. The next payment (or repricing) is scheduled for 8/15/1996, using the three month frequency from the fourth payment (or repricing) in the schedule.

Absolute patterns do not require the same rolling mechanism for synchronization. The next payment (or repricing) date from an absolute pattern is determined by the first month and day after the calendar period end date. If this date does not correspond to the next payment (or repricing) date from the detail record, the next payment (or repricing) date of the detail record supersedes the date of the pattern. From that point on in the process, the payment (or repricing) dates from the pattern are used.

The cash flow engine has been designed in this manner to allow greater flexibility in modeling payment and repricing patterns. However, this flexibility increases the importance of detail data accuracy to ensure that when discrepancies exist between detail data and patterns, the differences are intended.

Multiple Timeline Patterns (Payment Patterns Only)

To initialize a detail instrument record tied to a split pattern, the cash flow engine generates a separate record for each split. The current balance for each split record is calculated using the percentage apportioned to that split, as defined through the payment pattern interface. The original balance, original payment, and current payment columns are also apportioned according to the percentage defined through the interface.

For each timeline resulting from the split of a detail instrument record, the current payment date must be determined. The method for determining the payment date is the same as described for single timeline patterns with one exception. For these instruments, the next payment date from the original instrument record does not override the calculated next payment date. The date derived from rolling the origination date forward for relative timelines or locating the next date for absolute timeliness is assumed to be the correct payment date.

Related Topics

Initialization of Modeling Data and Parameters

Determination of Modeling Start and End Dates

Modeling start and end dates are determined by the type of processing and the instrument being processed, as shown in the following table:

Modeling Start and End Dates

Processing and instrument type	Start Sate	End Date
OFS Transfer Pricing Standard Calculation Mode - Adjustable	last reprice date	next reprice date
OFS Transfer Pricing Standard Calculation Mode - Fixed	origination date	maturity date
OFS Transfer Pricing Remaining Term Calculation Mode - Adjustable	effective date + 1 day	next reprice date
OFS Transfer Pricing Remaining Term Calculation Mode - Fixed	effective date + 1 day	maturity date

Oracle Transfer includes records for processing after filtering them using the calendar period end date and dataset group parameters such as ledger and input datasets.

For example, only records that have a value in the Calendar Period column of the database equal to the Calendar Period input as a run parameter for the Transfer Pricing Process rule are included.

Related Topics

Initialization of Modeling Data and Parameters

Initialization of Additionally Derived Data

The transfer pricing of adjustable rate instruments involves the following additional steps:

• Data reset to values consistent with the last reprice date

• Percent sold adjustment

Data Reset to Values Consistent with the Last Reprice Date

Oracle Transfer Pricing resets data to values consistent with the last reprice date by rolling back the next payment date by the payment frequency to the first payment date after the last reprice date. The application increases the remaining number of payments by the number of payments added in the rollback process.

The Last Reprice Date Balance is used in place of the current balance in a transfer pricing process. If the balance as of the last reprice date is not available, the application updates this column with the current balance. Oracle Transfer Pricing program has a special feature that re-amortizes the current payment if the following conditions are met:

• The last reprice date balance equals the current balance

• Payments occur between the last reprice date and the Calendar Period End Date

• The instrument is not tied to an amortization pattern or an amortization schedule

These three conditions signal the cash flow engine that the balance as of the last reprice date is not available and that the current balance should be used as a proxy.

Percent Sold Adjustment

Balances must be adjusted for participations:

• Current net balance = current par balance * (100 - percent sold)/100

• Current payment net = current payment * (100 - percent sold)/100

• Original net balance = original par balance * (100 - percent sold)/100

• Last reprice balance net = last reprice balance * (100 - percent sold)/100

• Original payment net = original payment * (100- percent sold)/100

Related Topics

Initialization of Modeling Data and Parameters

Processing Modeling Events

The cash flow engine models the following four events:

• Payment

• Payment Change

• Reprice

• Prepayment

When multiple events occur on the same day the cash flow engine processes them in the following order:

• Interest in Arrears

  1. Payment Calculation

  2. Payment

  3. Prepayment

  4. Reprice

• Interest in Advance

  1. Reprice

  2. Payment

  3. Prepayment

Note: For interest in advance instruments, payment calculation is not applicable. Payment calculation occurs only on conventionally amortizing instruments.

The cash flow engine processes an event as follows:

• Updates the dynamic information.

• Generates financial elements summarizing the event.

• Increments event dates to the next event date.

Related Topics

The Cash Flow Calculation Process

Payment Calculation Event

The cash flow data for payment calculation has the following characteristics:

Static Information: Conventional Adjustable and Payment Patterns

• Current Gross Rate

• Current Par Balance

• Amortization Term And Multiplier

• Amortization Type

• Adjustable Type Code

• Compounding Basis Code

Additional Information: Adjustable Negative Amortization (NGAM):

• Payment Increase Cycle

• Payment Increase Life

• Payment Decrease Cycle

• Payment Decrease Life

• Payment Change Frequency And Multiplier

• NGAM Equalization Frequency And Multiplier

• Original Payment Amount

• Dynamic Information

• Current Payment

Event Trigger: Transfer Pricing

• Cash flow transfer pricing of an Adjustable instrument

Event Triggers: Conventional Adjustable and Conventional Payment Patterns

• Reprice Event

Event Triggers: Adjustable Negative Amortization (NGAM)

• Next Payment Change Date

• NGAM Balance > NGAM Limit

• NGAM Equalization Date

Related Topics

Processing Modeling Events

Payment Calculation Steps

Payment calculation comprises the following steps:

1. Calculation of New Current Payment

2. Application of Periodic Payment Change Limits

3. Application of Lifetime Payment Change Limits

4. Negative Amortization (NGAM) Equalization

5. Update of Current Payment Field

1. Calculation of New Current Payment

Conventionally Amortizing Payment = Current Par Balancem / (1 / Current Ratec) x (1 - (1 + Current Ratec) ^ rem pmtsa)

Here:

• Current RateC = current compounded customer rate per payment

• rem pmtsa = remaining number of payments based on amortization

• Current Par Balancem = current balance at time of payment recalculation

For conventional schedules that reprice, payment recalculation does not occur. For patterns which reprice, payment recalculation does not occur during the repricing event. For these instruments, the payment is calculated at the time of payment. See: Payment Event.

Current Compounded Customer Rate per Payment

The customer rate must be adjusted to a rate per payment. If no compounding occurs, the rate can be divided by the payments per year. The following table illustrates how a current customer rate of 7.5% is adjusted to a rate per payment.

Example of Current Customer Rate Adjusted to a Rate per Payment

Payment Frequency	Calculation	Rate per Payment
monthly	7.5 ÷12	0.625
quarterly	7.5 ÷ 4	1.875
yearly	7.5 ÷ 1	7.5

If the instrument compounds, the rate must be adjusted for compounding. For monthly rates that compound daily, an average number of days assumption of 30.412 is used.

Remaining Number of Payments Based on Amortization

If the amortization term is equal to the original term, the calculation of the remaining number of payments is simple.

However to calculate the remaining number of payments when the amortization term is lesser or greater than the original term, the cash flow engine adds the amortization term to the origination date to determine the amortization end date. The cash flow engine calculates the remaining number of payments by determining the number of payments that can be made between the next payment date and the amortization end date, and adding one additional payment for the payment on the next payment date.

The cash flow engine calculates the remaining number of payments for patterns based on the payment frequency at the time of repricing. As with conventional instruments, the amortization end date is used for payment recalculation. The remaining term is calculated using the difference between the next payment date and the amortization end date. This term is divided by the active payment frequency and one additional payment is added to it for the payment on the next payment date.

2. Application of Periodic Payment Change Limits

Periodic payment change limits restrict the amount by which a payment installment can increase over its previous value. These limits are applied only when the payment installment recalculation is triggered by a payment adjustment date or a negative amortization limit. Because of these limits, the principal may continue to negatively amortize when the negative amortization limit has been reached. The following table describes payment conditions and related adjustments.

Payment Conditions and Related Adjustments

Condition	Adjustment
Increasing Payment: Newly Calculated Payment > (1 + (Payment Increase Lifer/100)) * Original Paymentr	Current Paymentm = (1+ (Payment Increase Lifer/100)) * Original Paymentr
Decreasing Payment: Newly Calculated Payment < (1 + (Payment Decrease Lifer/100)) * Original Paymentr	Current Paymentm = (1 + (Payment Decrease Lifer/100)) * Original Paymentr

3. Application of Lifetime Payment Change Limits

Lifetime payment cap and floor set the maximum and minimum amount for a payment installment. These limits are applied only when a payment recalculation is triggered by a payment adjustment date or a negative amortization limit. Because of these limits, principal may continue to negatively amortize when the negative amortization limit has been reached.

Payment Conditions and Related Adjustments

Condition	Adjustment
Increasing Payment: Newly Calculated Payment > (1 + (Payment Increase Lifer/100)) * Original Paymentr	Current Paymentm = (1+ (Payment Increase Lifer/100)) * Original Paymentr
Decreasing Payment: Newly Calculated Payment < (1 + (Payment Decrease Lifer/100)) * Original Paymentr	Current Paymentm = (1 + (Payment Decrease Lifer/100)) * Original Paymentr

4. Negative Amortization (NGAM) Equalization

If a payment recalculation is triggered by a NGAM equalization date, payment change limits do not apply. If the newly calculated payment is greater than the lifetime payment cap or less than the lifetime payment floor, the appropriate lifetime payment limit (cap/floor) is set equal to the newly calculated payment.

5. Update of Current Payment Field

Once all the payment limits have been applied, the new current payment is updated in memory for the processing of future events.

Related Topics

Processing Modeling Events

Payment Event

The cash flow data for payment event has the following characteristics:

• Static Information

• Dynamic Information

• Event Triggers

Static Information

• Amortization Type

• Current Payment

• Accrual Basis Code

• Current Gross Rate

• Current Net Rate

• Origination Date

• Payment Frequency And Multiplier

• Interest Type

• Compounding Basis Code

• Last Payment Date

Dynamic Information

• Current Par Balance

• Remaining Number Of Payments

• Negative Amortization (NGAM) Balance

Event Triggers

• Next Payment Date

• Maturity Date

Related Topics

Processing Modeling Events

Payment Event Steps

The payment event comprises the following steps:

1. Calculation of Interest Cash Flows

2. Calculation of Current Payment for Patterns and Schedules

3. Calculation of Principal Runoff

4. Performing Special Negative Amortization Check

5. Identifying Maturity Date Case

6. Update of Current Balance

7. Update of Remaining Number of Payments

8. Update of Next Payment Date

1. Calculation of Interest Cash Flows

The cash flow engine calculates the amount of interest to be paid on a payment date as described in the following table:

Interest Rate Calculation Formulas

Interest Cash Flow	Calculation
Interest cash flow gross	Current net par balance * gross rate per payment
Interest cash flow net	Current net par balance * net rate per payment

Note: Loans with amortization schedules based on the Rule of 78 are exceptions. These loans have a precomputed interest schedule. See: Example of the Rule of 78.

Rate per Payment: Accrual Adjustment

The annual coupon rate must be adjusted to a rate per payment. The accrual basis codes define how this adjustment should be made.

Accrual Basis Codes Example

The following table shows how using different accrual basis codes an annual coupon rate of 6 percent is adjusted to a rate per payment for a June 30 payment for an instrument that has a payment frequency of three months.

Accrual Basis Codes and Rate per Payment Adjustments

Accrual Basis Code	Payment Adjustment	Rate per Payment
30/360	(3*30)/360 * 6.0	1.500%
30/365	(3*30)/365 * 6.0	1.4795%
30/Actual	90/365 * 6.0	1.4795%
Actual/Actual	(30+31+30)/365 * 6.0	1.4959%
Actual/365	(30+31+30)/365 * 6.0	1.4959%
Actual/360	(30+31+30)/360 * 6.0	1.5167%

This formula assumes a single rate per payment period. If an instrument reprices multiple times within a payment period, only the last repricing event affects the interest cash flow.

Rate per Payment: Compounding Adjustment

The cash flow engine compounds the rate used in interest calculation if the compounding frequency is less than the payment frequency. The following table describes the interest rate compounding codes and the associated compounding formula.

Compounding Codes and Formula

Compounding Code	Calculation
Simple	No compounding
At Maturity	No compounding
Continuous	e^(rate per payment) -1
Daily	(1 + rate/365 or 366) ^ (days in payment) -1
Monthly, Quarterly, Semi-Annually, Annually	(1 + rate per pmt/cmp pds per pmt) ^ (cmp pds per pmt)

Rate per Payment: Stub and Extended Payment Adjustment

An adjustment may be made if the expected payment frequency (in days) is different from the actual payment frequency (in days). The number of days between the next payment date and the last payment date is compared to the payment frequency specified in days. The payment frequency specified in days depends on the month the payment occurs. If these numbers are not equal, the interest cash flow is adjusted by the following ratio:

(next payment date - last payment date)/payment frequency in days

This adjustment holds true for all payments other than the final payment. For the final payment, the number of days between the maturity date and the last payment before the maturity date is compared to the payment frequency specified in days. The payment frequency specified in days depends on the month in which the maturity date occurs. If these numbers are not equal, the interest cash flow is adjusted by the following ratio:

(maturity date - last payment date)/payment frequency in days

2. Calculation of Current Payment for Patterns and Schedules

For amortization patterns, the payment amount can be defined independently for each payment date. Therefore, on each payment, the payment amount must be calculated according to the characteristics defined for that date. The payment amounts depends on the following factors:

• Percent of Original Payment

• Percent of Current Payment

• Percent of Current Balance

• Percent of Original Balance

• Absolute Value

• Interest Only

Percent of Original Payment

You can choose to transfer price your product portfolio either in the Standard or in Remaining Term calculation mode. See: Transfer Pricing Process Rule and Calculation Modes, Oracle Transfer Pricing User Guide.

In the Standard calculation mode, the cash flow engine calculates the payment amount for each payment that falls between the last reprice date and the next reprice date (adjustable rate instruments) or between the origination date and maturity date (fixed rate instruments) by using the original payment from the instrument record and applying the pattern percent from the interface. The pattern percent is the percent of original payment specified in the interface for that payment.

In the Remaining Term calculation mode, the cash flow engine calculates the payment amount as follows:

On the first modeled payment on a detail instrument record, the amount in the current payment column is assumed to accurately represent the payment amount as of the next payment date. If this instrument record is partially sold, the current payment is multiplied by (100 - percent sold)/100 to get the net payment amount.

If this is the first payment made by a new business record, the payment amount is calculated using the original balance, original rate, and original number of payments.

On subsequent payment dates, the cash flow engine calculates the amount paid by multiplying the pattern percent by the amount in the original payment amount column, adjusted for percent sold, if applicable.

Percent of Current Payment

On the payment date, the cash flow engine determines the amount to be paid by first calculating a new payment according to the “active” characteristics, including the current balance, current rate, current payment frequency, and calculated remaining number of payments. The remaining number of payments is calculated by determining the amount of time remaining in the amortization term and dividing this term by the current payment frequency.

After the payment has been calculated, the pattern percent is applied.

Percent of Current Balance

Percent of Current Balance is applicable only for Level Principal payment patterns. On the first modeled payment, the amount in the current payment column is assumed to accurately represent the payment amount as of the next payment date. If the instrument is partially sold, the amount should be multiplied by (100 - percent sold)/100 to get the net payment amount. For all subsequent payments, the payment amount should be calculated at the time of payment by multiplying the outstanding balance by the pattern percent. However, for fixed rate instruments, modeling begins at the origination date, using the original balance. For adjustable rate instruments, modeling begins at the last reprice date, using the last reprice date balance.

Percent of Original Balance

Percent of Original Balance is applicable only for Level Principal payment patterns. On the first modeled payment, the amount in the current payment column is assumed to accurately represent the payment amount as of the next payment date. If the instrument is partially sold, the amount should be multiplied by (100 - percent sold)/100 to get the net payment amount.

For all subsequent payments, the payment amount should be calculated at the time of payment by multiplying the original balance, net of participations, by the pattern percent.

Absolute Value

On the first modeled payment, the amount in the current payment column is assumed to accurately represent the payment amount as of the next payment date. If the instrument is partially sold, the amount should be multiplied by (100 - percent sold)/100 to get the net payment amount.

For all subsequent payments, the absolute value amount from the pattern is used. If the instrument has a percent sold, the percent sold is applied to the absolute payment amount.

For standard transfer pricing, the absolute payment amount is used, adjusted for the participation percent.

Interest Only

On all interest only payments, the payment amount is calculated as the interest due on that date. No reference is made to the current payment column from the detail instrument record. Any payments in the current payment column are ignored.

3. Calculation of Principal Runoff

Principal runoff is a function of the amortization type of the instrument and the current payment. The current payment on a conventionally amortizing record represents the total principal and interest payment, while the current payment on a level principal record represents the principal portion of the total payment.

Simple Amortization

(code = 700, 802, and any Non-Amortizing Pattern Codes)

General case: Principal Runoff = 0

Interest Credited: -1 * interest cash flow gross

Conventional Amortization

(code = 100, 500, 600, 800, and any conventionally amortizing pattern codes)

Principal Runoff = current paymentm - interest cash flow gross

Level Principal Amortization

(code = 820, 801, and any level principal amortizing pattern codes)

Principal Runoff = current paymentm

Rule of 78 (code = 710)

Principal Runoff = current paymentm - interest cash flow gross

4. Performing Special Negative Amortization Check

If principal runoff is negative and the instrument record is adjustable negative amortization, then it must be ensured that the record is not exceeding negative amortization limits. As part of special negative amortization check, the cash flow engine verifies if the following condition holds true.

-1 * principal runoff + neg am balancem > neg am limitt /100 * original balancer

If this condition is true, the payment is not made. The payment is recalculated. See: Payment Event.

After the new payment has been calculated, the scheduled principal runoff is recalculated, based on the new payment information.

5. Identifying Maturity Date Case

If the payment date is also the maturity date, then the remaining balance must be paid off.

Principal At Maturity = Current Balancem - Scheduled Principal Runoff

6. Update of Current Balance

The current balance must be updated to reflect the principal portion of the payments and any interest credited.

Current Balancem = Current Balancem - Principal Runoff - Principal At Maturity + Interest Credited

7. Update of Remaining Number of Payments

After a payment has been made, the underlying information must be updated in preparation for the next event.

The remaining number of payments is reduced by 1. If remaining number of payments is zero, the modeling for this instrument is complete.

Remaining Paymentsm = Remaining Paymentsm - 1

8. Update of Next Payment Date

For standard amortization instruments, the next payment date is set equal to the current payment date plus the payment frequency.

Next payment datem = Current payment date + payment frequency

If an instrument has an amortization schedule, the next payment date is determined from the dates in the schedule table.

If an instrument has an amortization pattern, the next payment date is determined by incrementing the current payment date by the current payment frequency for relative patterns. For absolute patterns, the next payment date is determined by the next consecutive date in the pattern.

If the remaining number of payments is equal to 1, or the next payment date is greater than the maturity date, the next payment date is set equal to the maturity date.

Related Topics

Processing Modeling Events

Payment Event Steps for Interest-in-Advance Instruments

The following steps are applicable only to payment calculation for interest-in-advance records. Interest-in-advance instruments require their first payment to be made on the origination date. The last payment, made on the maturity date, is a principal only payment.

1. Determination of New Current Payment on Schedules and Patterns

   See: Calculation of Current Payment for Patterns and Schedules.

2. Calculation of Principal Runoff

   For interest-in-advance records, the principal runoff occurs before the interest cash flow is calculated. Because conventionally amortizing instruments cannot have interest-in-advance characteristics, amortizing interest-in-advance instruments are always level principal. Therefore, the principal runoff equals the current payment amount.

   For the payment on the maturity date, all remaining principal is also paid off.

3. Update Of Current Balance

   Before calculating the interest cash flow, the current balance must be updated for the amount of principal runoff. If the payment is the maturity date, the balance is set to zero, and no further calculations are necessary.

4. Calculation of Interest Cash Flow

   If the payment date is not the maturity date, an interest cash flow is made. The interest cash flow calculation for interest-in-advance instruments is similar to the interest in arrears calculation. The calculation differs in the count for number of days. Rather than counting from the last payment date to the current payment date, the number of days is counted from the current payment date to the next payment date.

5. Update of Remaining Number of Payments

   After a payment has been made, the underlying data must be updated in preparation for the next event. The remaining number of payments is reduced by 1.

6. Update Next Payment Date

   For standard amortization instruments, the next payment date is set equal to the current payment date plus the payment frequency.

   Next payment datem = Current payment date + payment frequency

   If the instrument has an amortization schedule, the next payment date is determined from the dates in the schedule table.

   If the instrument has an amortization pattern, the next payment date is determined by incrementing the current payment date by the current payment frequency for relative patterns. For absolute patterns, the next payment date is determined by the next consecutive date in the pattern.

   If the remaining number of payments is equal to 1, or the next payment date is greater than the maturity date, the next payment date is set equal to the maturity date.

Related Topics

Processing Modeling Events

Prepayment Event

The cash flow data for prepayment event has the following characteristics:

• Static Information

• Dynamic Information

• Additional Assumption Information

• Event Triggers

Static Information

• Current Gross Rate

• Current Net Rate

• Payment Frequency and Multiplier

• Origination Date

• Original Term

• Next Reprice Date

• Reprice Frequency

• Maturity Date

Dynamic Information

• Current Par Balance

• Current Payment

Additional Assumption Information

• Prepayment Assumption Rule

• Prepayment Table Rule

Event Triggers

• Next Payment Date

Related Topics

Processing Modeling Events

Prepayment Event Steps

The prepayment event comprises the following steps:

1. Update of the Value of the Prepayment Dimensions

2. Determination of the Base Annual Prepayment Rate

3. Adjustment for Seasonality

4. Selection of the Prepay in Full Option

5. De-annualization of the Prepayment Option

6. Adjustment of the Prepayment Rate for Stub or Extended Payments

7. Determination of the Prepayment Amount

8. Update of the Current Balance

9. Application of the Prepayment Factor to Current Payment

1. Update of the Value of the Prepayment Dimensions

Depending on the prepayment assumptions for a product, values for the prepayment dimensions may need to be updated. The prepayment assumptions for the product are defined in a Prepayment rule, which is then selected for the current processing run.

If the prepayment method is Constant Rate, these updates are not necessary. If the prepayment method is Arctangent, only the rate ratio need be calculated. For Prepayment Table method, the required updates depend on the dimension within the table for the proper origination date range.

The possible prepayment dimensions are as follows:

• Market Rate

• Coupon Rate

• Rate Difference

• Rate Ratio

• Original Term

• Repricing Frequency

• Remaining Term

• Expired Term

• Term to Reprice

Market Rate

The market rate is selected per product within the Prepayment rule. You must choose an interest rate code (IRC) from the list of IRCs contained in the active Historical Rates database. The chosen IRC provides the base value for the market rate.

Additionally, you must specify the term point you want to use for IRCs which are yield curves. There are three possible methods for you to select:

• Original Term

  The cash flow engine retrieves the rate from the term point equaling the original term on the instrument.

• Reprice Frequency

  The cash flow engine retrieves the rate from the term point equaling the reprice frequency of the instrument. If the instrument is fixed rate and, therefore, does not have a reprice frequency, the calculation retrieves the rate associated with the term point equaling the original term on the instrument.

• Remaining Term

  The cash flow engine retrieves the rate from the term point equaling the remaining term of the instrument.

  The market rate is determined by retrieving the proper rate and adding the user-input spread.

  Market Rate = f(Current Date, IRC, yield curve term) + spread

Coupon Rate

The coupon rate is the current gross rate of the instrument record (as of the current date in the forecast).

Rate Difference

The rate difference is the spread between the coupon rate and the market rate. Before calculating this dimension, the market rate must be retrieved.

Rate Difference = Coupon Rate - Market Rate

Rate Ratio

The rate ratio is the proportional difference between the coupon rate and the market rate. Before calculating this dimension, the market rate must be retrieved.

Rate Ratio = Coupon Rate/Market Rate

Original Term

The original term is retrieved from the original term of the instrument. If the original term is expressed in months, no conversion is necessary. Otherwise, the following calculations are applied:

Original Termmonths = ROUND((Original Termdays)/30.412)

Original Termmonths = Original Termyears*12

Reprice Frequency

The value for reprice frequency depends on the adjustable type code and the tease characteristics of the instrument data.

• Fixed Rate

  If the instrument is fixed rate, as designated by an adjustable type code = fixed (code value = “0”), the original term, as defined above, is used as the reprice frequency.

  Reprice Frequency = Original Term (months)

• Non-Tease Floating

  If the adjustable type of the instrument is floating (code value of “30” or “50” and not in a tease period), the reprice frequency is assumed to be one day, which when rounded to a month value, becomes 0 months.

  Reprice Frequency = 0 months

• Non-Tease Adjustable

  If the adjustable type of the instrument is adjustable (code value of “250”) and not in a tease period, the reprice frequency columns is used. All cases where terms are not expressed in months should be translated into months, calculated as follows:

  Reprice Frequencymonths = Reprice Frequencyyears*12

  Reprice Frequencymonths = Round (Reprice Frequency days/30.412

• Teased Loans

  The tease period is identified by a tease end date > current date. The reprice frequency during the tease period is calculated as follows (rounded to the nearest whole number of months).

  Reprice Frequency = ROUND((Tease End Date - Origination Date) /30.412)

Remaining Term

The remaining term value represents the remaining number of months until maturity. The value is rounded to the nearest whole number of months.

Remaining Term = ROUND((Maturity Date - Current Date)/30.412)

Expired Term (Age)

The expired term represents the age of the instrument. It represents the time elapsed since the origination of the instrument. The value is rounded to the nearest whole number of months.

Expired Term = ROUND((Current Date - Origination Date)/30.412)

Term to Reprice

As with reprice frequency, the calculation of term to reprice depends on the adjustable type code and tease characteristics of the instrument characteristics.

• Fixed Rate

  If the instrument is fixed rate, as designated by an adjustable type code = fixed (code value = “0”), the term to reprice is calculated in the same manner as remaining term. The value is rounded to the nearest whole number of months.

  Term to Reprice = ROUND (Maturity Date - Current Date/30.412)

• Non-Tease Floating

  If the adjustable type of the instrument is floating (code value of “30” or “50”), and is not in its tease period, the reprice frequency is taken as 1 day. The term to reprice is assumed to be one day, which when rounded to a month value, becomes 0 months.

  Term to Reprice = 0 months

• Non-Tease Adjustable

  If the adjustable type of the instrument is adjustable (code value of “250”) and not in its tease period, the term to reprice is calculated as the difference between the current date and the next reprice date. The value is rounded to the nearest whole number of months.

  Term to Reprice = ROUND((Maturity Date - Current Date)/30.412)

• Teased Loans

  The tease period is identified by a tease end date > current date. The term to reprice, while in this period, is calculated as the difference between the current date and the tease end date. The value is rounded to the nearest whole number of months.

  Term to Reprice = ROUND((Tease End Date - Current Date)/30.412)

2. Determination of the Base Annual Prepayment Rate

The method for determining the annual prepayment rate depends on the prepayment method.

Constant Rate

Constant prepayment rates can vary for different origination date ranges. The rate is determined by finding the proper range of origination dates and using the constant rate from this range.

Base Annual Prepayment Rate = Constant Rate

Arctangent

The arctangent formula describes the relationship between prepayments and the ratio of coupon rate to market rate. Four coefficients, to which you enter coefficients, define the shape of the curve. These coefficients can vary by origination date range.

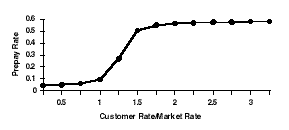
Base Annual Prepayment (PP) Rate = Coeff1 - Coeff2 * ARCTANGENT(Coeff3* (Coeff4 - Rate Ratio))

The following graphic illustrates the base annual prepayment rate based on the arctangent formula.

Prepayment Table

Under the Prepayment Table method, a Prepayment Table rule is referenced within the Prepayment rule for a particular product and origination date range. This prepayment table may be factored by a coefficient to scale the prepayment rates which reside in the table up or down. The prepayment table factor is also defined per product, currency, and origination date.

The Prepayment Table rule contains a table of prepayment rates dimensioned by other characteristics. The Prepayment Table rule can hold a maximum of three dimensions. For each dimension, you can define the lookup method along that dimension, either range or interpolate.

• Range Lookup

  Range Lookup treats the nodes within the dimension as a starting value for a range which extends to the next node dimension. For example, take an original term dimension with node values of 0, 12, and 24. The range lookup treats these values as three sets of ranges: 0 to 11, 12 to 23, and >= 24.

• Interpolation Lookup

  If the interpolation method is selected, the lookup applies straight line interpolation to determine the proper prepayment rate for values which fall between nodes.

• Lookups Outside the Given Range

  For both lookup methods, lookup for values less than the lowest node value receives the prepayment rate associated with the lowest node. Values greater than the highest node receive the prepayment rate associated with the highest node.

Along each dimension of the table, range lookup or interpolation is performed to pinpoint the proper prepayment rate from the table. Once the prepayment rate is retrieved from the prepayment table, the prepayment table factor is applied to this rate.

Base Annual Prepayment Rate = PPTableFactor * PPTableLOOKUP(dimensionx, dimensiony, dimensionz)

3. Adjustment for Seasonality

For each prepayment method, seasonality factors can be applied to adjust the prepayment rate. The seasonality factors are defined per month. The month of the current date is used to determine the proper seasonality factor to use.

Annual Prepayment (PP) Rate = Seasonality Factor (Current Month) * Base Annual PP Rate

4. Selection of the Prepay in Full Option

If the adjusted final prepayment rate is equal to 100%, the instrument is paid off in full.

5. De-annualization of the Prepayment Option

The annual prepayment rate is adjusted to a rate per payment. The formula is as follows:

Prepay Factor = (1-(1- Annual PPRate)^(1/Payments per Year))

6. Adjustment of the Prepayment Rate for Stub or Extended Payments

The prepayment rate per payment is adjusted if the payment is a stub or extended payment. This adjustment is made in the same manner that interest cash flows are adjusted, as follows:

Adjusted prepay factor = Prepay Factor * (next payment date - last payment date) / (pmt frequency in days)

7. Determination of the Prepayment Amount

The amount of runoff due to prepayments is calculated. The prepay factor is applied to the current balance.

Prepay Runoff = Current Balance * Prepay Factor

8. Update of the Current Balance

The current balance must be reduced by the amount of prepay runoff.

Current Balance = Current Balance - Prepay Runoff

9. Application of the Prepayment Factor to Current Payment

An option exists in the Prepayment rule to reduce the payment proportionally to reflect the amount of principal that has been prepaid. If the prepayment treatment is Refinance, the current payment is reduced as follows:

Current Payment = Current Payment * (1 - Prepay Factor)

If the payment treatment is Curtailment, the current payment will remain constant, effectively reducing the term of the instrument.

Related Topics

Processing Modeling Events

Reprice Event

The cash flow data for the repricing event has the following characteristics:

• Static Information

• Dynamic Information

• Event Triggers

Important: The modeling of an adjustable rate instrument begins at the last reprice date and ends at the next reprice date, with the next repricing date treated like a maturity date for the instrument. Therefore, no repricing events occur during a transfer pricing process.

Static Information:

• Adjustable Type Code

• Interest Rate Code

• Transfer Rate Interest Rate code

• Net Margin

• Net Margin Code

• Gross Margin

• Transfer Rate Margin

• Reprice Frequency and Multiplier

• Rate Cap Life

• Rate Floor Life

• Rate Increase Period

• Rate Decrease Period

• Rate Set Lag and Multiplier

• Rate Change Minimum

• Rate Change Rounding Code

• Rate Change Rounding Factor

Dynamic Information

• Current Gross Rate

• Current Net Rate

Event Triggers

• Bucket Start Date

• Tease End Date

• Next Reprice Date

Detail Cash Flow Data

The following table describes detail cash flow data.

Tip: The values of the Event Use codes used in the table are as follows:

• I: Initialization of record

• P: Payment

• PC: Payment recalculation

• PP: Prepayment

• R: Reprice

• D: Deferred amortization

Detail Cash Flow Data

Column Name	Column Description	Column Type	Event use
ID_NUMBER	Unique identifier	static	I
LINE_ITEM_ID	Dimension member value that determines the financial account type of detail instrument	static	I
ADJUSTABLE_TYPE_CODE	Determines whether repricing occurs, and, if it occurs, whether it occurs according to reprice dates or bucket dates	static	R
ACCRUAL_BASIS_CODE	Method of accrual used to determine the rate per payment	static	P
AMRT_TERM & AMRT_TERM_MULT	Determines the time over which principal is amortized. Used in payment recalculation.	static	P, PC
AMRT_TYPE_CODE	Determines the method for amortizing principal. Used to match to payment pattern data.	static	PC
CUR_PAYMENT	Amount of current payment. Meaning depends on amortization type code.	dynamic	P, PC
CUR_PAR_BAL	Balance on which principal runoff, interest cash flows, and deferred runoff are based	dynamic	P, PC, PP
CUR_NET_RATE	Interest rate that the financial institution pays/receives	dynamic	P, R, PC, PP
CUR_GROSS_RATE	Interest rate that the customer pays/receives. Used in determining payments and prepayments.	dynamic	P, R, PC, PP
DEFERRED_CUR_BAL	Holds current unamortized premium, discount, fees, and costs	dynamic	D
ISSUE_DATE	Date instrument is recognized as on-the-books		I
INT_TYPE_CODE	Determines how interest is calculated and accrued	static	P
INSTRUMENT_TYPE_CODE	Used to match a schedule instrument record to its scheduled payment dates and amounts	static	I
LAST_PAYMENT_DATE	Date of last payment before the calendar period end date. Used to calculate days in first payment for interest in arrears instruments and to calculate accruals before the first payment in interest in advance instruments.	static	P
LRD_BALANCE	Balance as of last reprice date	static	I
LAST_REPRICE_DATE	Date instrument rate repriced last	static	I
MATURITY_DATE	Date of final payment	static	P, PP
NEG_AMRT_AMT	Amount of current balance due to negative amortization of interest payments	dynamic	P
NEG_AMRT_EQ_DATE	Date an instrument fully re-amortizes, irrespective of payment caps	event trigger	PC
NEG_AMRT_EQ_FREQ &
NEG_AMRT_EQ_MULT	Frequency of negative amortization equalization events. 0 denotes negative amortization equalization never occurs.	static	PC
NEG_AMRT_LIMIT	Maximum possible amount by which an instrument can negatively amortize. Stored as a percent of original balance.	event trigger	PC
NEXT_PAYMENT_DATE	Date of next payment	event trigger	P, PC
NEXT_REPRICE_DATE	Date of next rate change	event trigger	R, PP
ORG_PAYMENT_AMT	Payment used for cash flow transfer pricing of fixed rate records. Used by pattern instruments to calculate payment amount.	static	PC,I
ORG_PAR_BAL	Used in conjunction with negative amortization limit to determine the maximum amount that instrument can negatively amortize. Used for Rule of 78 schedules. Used by pattern instruments to calculate payment amount.	static	PC,I
ORG_TERM & ORG_TERM_MULT	Time from origination date to maturity date. Used in determining whether an instrument balloons for payment recalculation purposes.	static	PC,PP
ORIGINATION_DATE	Determines age of instrument for prepayments. Used in calculating remaining amortization term. Used in determining payment number in pattern records.	static	PP,PC
PERCENT_SOLD	Determines net balance	static	I
PMT_ADJUST_DATE	Date of next scheduled payment recalculation for negative amortization instruments	event trigger	PC
PMT_CHG_FREQ & PMT_CHG_FREQ_MULT	Frequency of regular payment change calculation for negative amortization instruments only. 0 denotes that payment never changes.	static	PC
PMT_DECR_CYCLE	Maximum possible percent decrease in payment from its previous value	static	PC
PMT_DECR_LIFE	Minimum payment amount. Stored as a percent of original payment amount. Can be overwritten on negative amortization equalization dates.	static	PC
PMT_FREQ & PMT_FREQ_MULT	Frequency of payments. Should be set equal to original term if the instrument is bullet requiring principal and interest to be paid at maturity date, or has the other asset, other liability, interest income, interest expense, non-interest income, or non-interest expense account type.	static	P, PC, PP
PMT_INCR_CYCLE	Maximum possible percent increase in the value of a payment	static	PC
PMT_INCR_LIFE	Maximum payment amount. Stored as a percent of original payment amount. Can be overwritten on negative amortization equalization dates.	static	PC
RATE_CAP_LIFE	Maximum value to which current rate can reprice	static	R
RATE_CHG_MIN	Minimum amount by which current rate must change before a rate change occurs	static	R
RATE_CHG_RND_CODE	Type of rounding to be applied to current rate	static	R
RATE_CHG_RND_FAC	Precision of rounding. 0 denotes no rounding.	static	R
RATE_DECR_CYCLE	Maximum amount by which rate can decrease within a repricing period	static	R
RATE_FLOOR_LIFE	Minimum value to which current rate can fall upon repricing	static	R
RATE_INCR_CYCLE	Maximum amount by which rate can increase within a repricing period	static	R
RATE_SET_LAG & RATE_SET_LAG_MULT	Time lag used when repricing. Used to determine rate set date on reprice event.	static	R
REMAIN_NO_PMTS	Number of payments left to be made on an instrument from the calendar period end date to the maturity date	dynamic	P, PC
REPRICE_FREQ & REPRICE_FREQ_MULT	Frequency by which an instrument reprices. 0 denotes fixed rate.	static	R, PP
ORG_PAYMENT_AMT	Payment used for cash flow transfer pricing of fixed rate records	static	I
TEASER_END_DATE	Date that a teased instrument begins repricing	event trigger	R, PP
NET_MARGIN_CODE	Defines relationship between gross rate and net rate. 0 denotes floating net rate. 1 denotes constant net rate.	static	R

Related Topics

Overview of Cash Flow Calculations

Financial Element Calculations

The following table describes financial element calculations.

Tip: The Account Type Processing column of the table specifies for which account types financial elements are processed. The values of the codes used in the Account Type Processing column of the table are as follows:

• B: Balance only

• I: Interest only

• DCF: Detail Cash Flow

• N: Non Interest

Financial Element Calculations

Financial Element Description	Financial Element Number	Averaging Type	Weighting Factor	Account Type Processing
After Reprice Balance	255	At Last		DCF
After Reprice Gross Rate	290	At Last	After Reprice Balance	DCF
After Reprice Net Rate	300	At Last	After Reprice Balance	DCF
After Reprice Transfer Rate	310	At Last	After Reprice Balance	DCF
Average Balance	140	Daily Average		B, DCF
Average Gross Rate	150	Daily Average	Average Balance	DCF
Average Rem Term Transfer Rate	172
Average Net Rate	160	Daily Average	Average Balance	DCF
Average Transfer Rate	170	Daily Average	Average Balance	DCF
Before Reprice Balance	250	At First		DCF
Before Reprice Gross Rate	260	At First	Before Reprice Balance	DCF
Before Reprice Net Rate	270	At First	Before Reprice Balance	DCF
Before Reprice Transfer Rate	280	At First	Before Reprice Balance	DCF
Beginning Balance	60	At First		B, DCF
Beginning Gross Rate	70	At First	Beginning Balance	DCF
Beginning Net Rate	80	At First	Beginning Balance	DCF
Beginning Transfer Rate	90	At First	Beginning Balance	DCF
Charge/Credit Rem Term	452
Current Option Cost	173
Current Option Cost Charge/Credit	453
Deferred Average Balance	530	Daily Average		DCF
Deferred Ending Balance	520	At Last		DCF
Deferred Runoff	540	Accrual		DCF
Discount Rate	490	AVG_BY_DAYS_WTD		DCF
Ending Balance	100	At Last		B, DCF
Ending Gross Rate	110	At Last	Ending Balance	DCF
Ending Net Rate	120	At Last	Ending Balance	DCF
Ending Transfer Rate	130	At Last	Ending Balance	DCF
Fully Indexed Gross Rate	320	Sum		DCF
Fully Indexed Net Rate	330	Sum		DCF
Historic Option Cost	171
Current Option Cost Charge/Credit	453
Interest Accrual - Gross	445	Accrual		DCF, I
Interest Accrual - Net	440	Accrual		DCF, I
Interest Accrual - Transfer Rate	450	Accrual		DCF, I
Interest Cash Flow Gross	435	Sum		DCF, I
Interest Cash Flow Net	430	Sum		DCF, I
Interest Cash Flow Transfer Rate	437	Sum		DCF, I
Interest Credited	480	Sum		DCF
Lifetime Cap Balance	580	Daily Average		DCF
Lifetime Cap Effect	600	Accrual		DCF
Lifetime Cap Rate	590	Daily Average	Lifetime Cap Balance	DCF
New Add Balance	340	Sum		DCF
New Add Gross Rate	350	Sum	New Add Balance	DCF
New Add Net Rate	360	Sum	New Add Balance	DCF
New Add Transfer Rate	370	Sum	New Add Balance	DCF
NGAM Balance	640	Daily Average		DCF
NGAM Interest	650	Accrual		DCF
Non-Interest Income	455	Sum		N
Non-Interest Expense	457	Sum		N
Periodic Cap Balance	550	Daily Average		DCF
Periodic Cap Effect	570	Accrual		DCF
Periodic Cap Rate	560	Daily Average	Periodic Cap Balance	DCF
Prepay Balance	515	Sum		DCF
Prepay Rate (Annual)	510	Sum	Prepay Balance	DCF
Prepay Runoff	180	Sum		DCF
Prepay Runoff	182	Sum		DCF
Present Value of the Total Cash Flow	495	SUM		DCF
Present Value of the Transfer Rate Interest Cash Flow	497	SUM		DCF
Roll Add Balance	380	Sum		DCF
Roll Add Gross Rate	390	Sum		DCF
Roll Add Net Rate	400	Sum		DCF
Roll Add Transfer Rate	410	Sum		DCF
Scheduled Principal Runoff	190	Sum		DCF
Tease Balance	610	Daily Average		DCF
Tease Effect	630	Accrual		DCF
Tease Rate	620	Daily Average	Tease Balance	DCF
Timing of Prepay Runoff (positive)	181	Sum	Prepay Runoff (positive)	DCF
Prepay Runoff (negative)	182	Sum		DCF
Timing of Prepay Runoff (negative)	183	Sum	Prepay Runoff (negative)	DCF
Timing of Total Runoff (positive)	211	Sum	Total Runoff (positive)	DCF
Total Runoff (negative)	212	Sum		DCF
Timing of Total Runoff (negative	213	Sum	Total Runoff (negative)	DCF
Total Runoff	210	Sum		DCF
Total Runoff (negative)	212	Sum		DCF
Total Runoff Gross Rate	220	Sum	Total Runoff	DCF
Total Runoff Net Rate	230	Sum		DCF
Total Runoff Transfer Rate	240	Sum		DCF
Weighted Average Term	500	Sum	Ending Balance	DCF

Related Topics

Overview of Cash Flow Calculations

Example of the Rule of 78

The Rule of 78 denotes an approach used by banks to formulate a loan amortization schedule. Also known as The Rule of the Sum of the Digits, this method of computing unearned interest is used on installment loans with add-on interest. The number 78 is based on the sum of the digits from 1 to 12. This approach causes a borrower to pay more interest at the beginning of the loan when there is more money owed and less interest as the obligation is reduced.

This example of the Rule of 78 is based on a 12 month loan with current payment installment of $93.33 and original balance of $1,000.00.

1. Sum all principal and interest payments made over the life of the instrument:

   ∑ Cash Flow

   = current payment * total number of payments

   = $93.33 * 12

   = $1,120.00

2. Determine total amount of interest paid over the life of the instrument.

   ∑ Interest

   = ∑ cash flow - original par balance

   = $1,120.00 - $1,000.00

   = $120.00

3. Sum the payment numbers.

   ∑ Payments

   = total num of payments * (total num of payments + 1)/2

   = 12 * 13/2

   = 78

4. Calculate principal and interest amount at each payment.

   Interest = ∑ interest * (payments remaining/∑ payments)

   Principal = current payment - interest

   The following table describes the Rule of 78 calculations for this example.

   Rule of 78 Calculations

   Month	Interest Calculation	Interest	Principal Calculation	Principal	Remaining Balance
   1	120 * 12/78	$18.46	93.33-18.46	$74.87	$925.13
   2	120 * 11/78	$16.92	93.33-16.92	$76.41	$848.72
   3	120 * 10/78	$15.38	93.33-15.38	$77.95	$770.77
   4	120 * 9/78	$13.85	93.33-13.85	$79.48	$691.29
   5	120 * 8/78	$12.31	93.33-12.31	$81.02	$610.27
   6	120 * 7/78	$10.77	93.33-10.77	$82.56	$527.71
   7	120 * 6/78	$9.23	93.33-9.23	$84.10	$443.61
   8	120 * 5/78	$7.69	93.33-7.69	$85.64	$357.97
   9	120 * 4/78	$6.15	93.33-6.15	$87.18	$270.79
   10	120 * 3/78	$4.61	93.33-4.61	$88.72	$182.07
   11	120 * 2/78	$3.08	93.33-3.08	$90.25	$91.82
   12	120 * 1/78	$1.54	93.33-1.54	$91.79	$0.00

Related Topics

Overview of Cash Flow Calculations