Quadruple-Precision Floating Point

The standard defines the encoding for the quadruple-precision floating-point data type quadruple (128 bits or 16 bytes). The encoding used is the IEEE standard for normalized quadruple-precision floating-point numbers [1]. The standard encodes the following three fields, which describe the quadruple-precision floating-point number.

S: The sign of the number. Values 0 and 1 represent positive and negative respectively. One bit.

E: The exponent of the number, base 2. Fifteen bits are in this field. The exponent is biased by 16383.

F: The fractional part of the number's mantissa, base 2. One hundred eleven bits are in this field.

Therefore, the floating-point number is described by:

(-1)**S * 2**(E-Bias) * 1.F

Declaration

quadruple identifier; 

Quadruple-Precision Floating Point Encoding

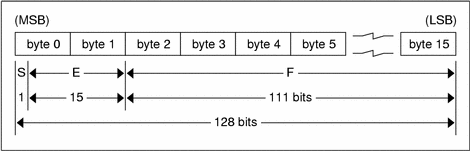
Just as the most-significant and least-significant bytes of an integer are 0 and 3, the most-significant and least-significant bits of a quadruple-precision floating- point number are 0 and 127. The beginning bit, and most-significant bit, offsets of S, E, and F are 0, 1, and 16 respectively. These offsets refer to the logical positions of the bits, not to their physical locations, which vary from medium to medium.

Consult the IEEE specifications about the encoding for signed zero, signed infinity (overflow), and de-normalized numbers (underflow) [1]. According to IEEE specifications, the NaN (not a number) is system dependent and should not be used externally.