Key Encryption

With most modern cryptography, the ability to keep encrypted information secret is based not on the cryptographic algorithm, which is widely known, but on a key. A key is a number that must be used with the algorithm to produce an encrypted result or to decrypt previously encrypted information. For information about encryption and decryption with keys, see the following sections:

• Symmetric-Key Encryption

• Public-Key Encryption

• Key Length and Encryption Strength

Symmetric-Key Encryption

With symmetric-key encryption, the encryption key can be calculated from the decryption key, and vice versa. With most symmetric algorithms, the same key is used for both encryption and decryption. The following figure shows a symmetric-key encryption.

Figure 5–12 Symmetric-Key Encryption

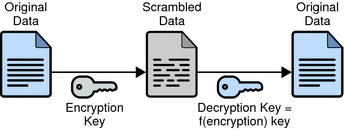
Implementations of symmetric-key encryption can be highly efficient, so that users do not experience any significant time delay as a result of the encryption and decryption. Symmetric-key encryption also provides a degree of authentication, since information encrypted with one symmetric key cannot be decrypted with any other symmetric key. Thus, as long as the symmetric key is kept secret by the two parties using it to encrypt communications, each party can be sure that it is communicating with the other as long as the decrypted messages continue to make sense.

Symmetric-key encryption is effective only if the symmetric key is kept secret by the two parties involved. If anyone else discovers the key, it affects both confidentiality and authentication. A person with an unauthorized symmetric key not only can decrypt messages sent with that key, but can encrypt new messages and send them as if they came from one of the two parties who were originally using the key.

Symmetric-key encryption plays an important role in the SSL protocol, which is widely used for authentication, tamper detection, and encryption over TCP/IP networks. SSL also uses techniques of public-key encryption, which is described in the next section.

Public-Key Encryption

The most commonly used implementations of public-key encryption are based on algorithms patented by RSA Data Security. Therefore, this section describes the RSA approach to public-key encryption.

Public-key encryption (also called asymmetric encryption) involves a pair of keys—a public key and a private key—associated with an entity that needs to authenticate its identity electronically or to sign or encrypt data. Each public key is published, and the corresponding private key is kept secret. The following figure shows a simplified view of the way public-key encryption works.

Figure 5–13 Public-Key Encryption

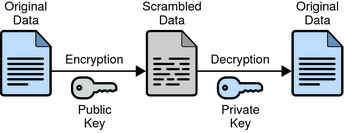
Public—key encryption lets you distribute a public key, and only you can read data encrypted by this key. In general, to send encrypted data to someone, you encrypt the data with that person’s public key, and the person receiving the encrypted data decrypts it with the corresponding private key.

Compared with symmetric-key encryption, public-key encryption requires more computation and is therefore not always appropriate for large amounts of data. However, it’s possible to use public-key encryption to send a symmetric key, which can then be used to encrypt additional data. This is the approach used by the SSL protocol.

As it happens, the reverse of the scheme shown in Figure 5–13 also works: data encrypted with your private key can be decrypted with your public key only. This would not be a desirable way to encrypt sensitive data, however, because it means that anyone with your public key, which is by definition published, could decrypt the data. Nevertheless, private-key encryption is useful, because it means you can use your private key to sign data with your digital signature—an important requirement for electronic commerce and other commercial applications of cryptography. Client software can then use your public key to confirm that the message was signed with your private key and that it hasn’t been tampered with since being signed. Digital Signatures and subsequent sections describe how this confirmation process works.

Key Length and Encryption Strength

The strength of encryption is related to the difficulty of discovering the key, which in turn depends on both the cipher used and the length of the key. For example, the difficulty of discovering the key for the RSA cipher most commonly used for public-key encryption depends on the difficulty of factoring large numbers, a well-known mathematical problem.

Encryption strength is often described in terms of the size of the keys used to perform the encryption: in general, longer keys provide stronger encryption. Key length is measured in bits. For example, 128-bit keys for use with the RC4 symmetric-key cipher supported by SSL provide significantly better cryptographic protection than 40-bit keys for use with the same cipher. Roughly speaking, 128-bit RC4 encryption is 3 x 10²⁶ times stronger than 40-bit RC4 encryption.

Different ciphers may require different key lengths to achieve the same level of encryption strength. The RSA cipher used for public-key encryption, for example, can use only a subset of all possible values for a key of a given length, due to the nature of the mathematical problem on which it is based. Other ciphers, such as those used for symmetric key encryption, can use all possible values for a key of a given length, rather than a subset of those values. Thus a 128-bit key for use with a symmetric-key encryption cipher would provide stronger encryption than a 128-bit key for use with the RSA public-key encryption cipher. This difference explains why the RSA public-key encryption cipher must use a 512-bit key (or longer) to be considered cryptographically strong, whereas symmetric key ciphers can achieve approximately the same level of strength with a 64-bit key. Even this level of strength may be vulnerable to attacks in the near future.