Forward and Inverse FFT Routines
The following tables list the names of the FFT routines and their calling sequence. Double precision routine names are in square brackets. See the individual man pages for detailed information on the data type and size of the arguments.
|
|
Oracle Developer Studio Performance Library FFT routines use the following arguments.
OPT: Flag indicating whether the routine is called to initialize or to compute the transform.
N1, N2, N3: Problem dimensions for one, two, and three dimensional transforms.
X: Input array where X is of type COMPLEX if the routine is a complex-to-complex transform or a complex-to-real transform. X is of type REAL for a real-to-complex transform.
Y: Output array where Y is of type COMPLEX if the routine is a complex-to-complex transform or a real-to-complex transform. Y is of type REAL for a complex-to-real transform.
LDX1, LDX2 and LDY1, LDY2: LDX1 and LDX2 are the leading dimensions of the input array, and LDY1 and LDY2 are the leading dimensions of the output array. The FFT routines allow the output to overwrite the input, which is an in-place transform, or to be stored in a separate array apart from the input array, which is an out‐of‐place transform. In complex-to-complex transforms, the input data is of the same size as the output data. However, real-to-complex and complex-to-real transforms have different memory requirements for input and output data. Care must be taken to ensure that the input array is large enough to accommodate the transform results when computing an in-place transform.
TRIGS: Array containing the trigonometric weights.
IFAC: Array containing factors of the problem dimensions. The problem sizes are as follows:
Linear FFT: Problem size of dimension N1
Two-dimensional FFT: Problem size of dimensions N1 and N2
Three-dimensional FFT: Problem size of dimensions N1, N2, and N3
While N1, N2, and N3 can be of any size, a real-to-complex or a complex-to-real transform can be computed most efficiently when
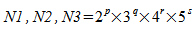 ,
,and a complex-to-complex transform can be computed most efficiently when
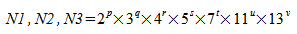 ,
,where p, q, r, s, t, u, and v are integers and p, q, r, s, t, u, v ≥ 0.
-
WORK: Workspace whose size depends on the routine and the number of threads that are being used to compute the transform if the routine is parallelized.
-
LWORK: Size of workspace. If LWORK is zero, the routine will allocate a workspace with the required size.
-
SCALE: A scalar with which the output is scaled. Occasionally in literature, the inverse transform is defined with a scaling factor of 1/N1 for one-dimensional transforms, 1/(N1 × N2) for two-dimensional transforms, and 1/(N1 × N2 × N3) for three-dimensional transforms. In such case, the inverse transform is said to be normalized. If a normalized FFT is followed by its inverse FFT, the result is the original input data. The Oracle Developer Studio Performance Library FFT routines are not normalized. However, normalization can be done easily by calling the inverse FFT routine with the appropriate scaling factor stored in SCALE.
-
ERR: A flag returning a nonzero value if an error is encountered in the routine and zero otherwise.
Linear FFT Routines
Linear FFT routines compute the FFT of real or complex data in one dimension only.
The data can be one or more complex or real sequences. For a single sequence, the
data is stored in a vector. If more than one sequence is being transformed, the
sequences are stored column-wise in a two-dimensional array and a one-dimensional
FFT is computed for each sequence along the column direction. The
linear forward FFT routines compute:
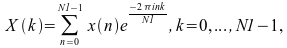 where
where
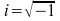 .
.
The inverse FFT routines compute
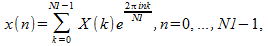
With the forward transform, if the input is one or more complex sequences of size N1, the result will be one or more complex sequences, each consisting of N1 unrelated data points. However, if the input is one or more real sequences, each containing N1 real data points, the result will be one or more complex sequences that are conjugate symmetric. That is:
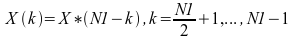
The imaginary part of X(0) is always zero. If
N1 is even, the imaginary part of
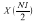 is also zero. Both zeros are stored explicitly. Because the second
half of each sequence can be derived from the first half, only
is also zero. Both zeros are stored explicitly. Because the second
half of each sequence can be derived from the first half, only
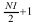 complex data points are computed and stored in the output array.
Here and elsewhere in this chapter, integer division is rounded down.
complex data points are computed and stored in the output array.
Here and elsewhere in this chapter, integer division is rounded down.
With the inverse transform, if an N1-point
complex-to-complex transform is being computed, then N1
unrelated data points are expected in each input sequence and
N1 data points will be returned in the output array.
However, if an N1-point complex-to-real transform is
being computed, only the first 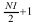 complex data points of each conjugate symmetric input sequence
are expected in the input, and the routine will return N1
real data points in each output sequence.
complex data points of each conjugate symmetric input sequence
are expected in the input, and the routine will return N1
real data points in each output sequence.
For each value of N1, either the forward or the inverse routine must be called to compute the factors of N1 and the trigonometric weights associated with those factors before computing the actual FFT. The factors and trigonometric weights can be reused in subsequent transforms as long as N1 remains unchanged.
The following table Table 12 lists the single precision linear FFT routines and their purposes. For routines that have two-dimensional arrays as input and output, Table 12 also lists the leading dimension requirements. The same information applies to the corresponding double precision routines except that their data types are double precision and double complex. See Table 12 for the mapping. See the individual man pages for a complete description of the routines and their arguments.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Note - Note the following about the table Table 12:
-
LDX1 is the leading dimension of the input array.
-
LDY1 is the leading dimension of the output array.
-
N1 is the first dimension of the FFT problem.
-
N2 is the second dimension of the FFT problem.
-
When calling routines with OPT = 0 to initialize the routine, the only error checking that is done is to determine if N1 < 0
The following example shows how to compute the linear real-to-complex and complex-to-real FFT of a set of sequences.
Example 10 Linear Real-to-Complex FFT and Complex-to-Real FFTmy_system% cat testscm.f
PROGRAM TESTSCM
IMPLICIT NONE
INTEGER :: LW, IERR, I, J, K, LDX, LDC
INTEGER,PARAMETER :: N1 = 3, N2 = 2, LDZ = N1,
$ LDC = N1, LDX = 2*LDC
INTEGER, DIMENSION(:) :: IFAC(128)
REAL :: SCALE
REAL, PARAMETER :: ONE = 1.0
REAL, DIMENSION(:) :: SW(N1), TRIGS(2*N1)
REAL, DIMENSION(0:LDX-1,0:N2-1) :: X, V, Y
COMPLEX, DIMENSION(0:LDZ-1, 0:N2-1) :: Z
* workspace size
LW = N1
SCALE = ONE/N1
WRITE(*,*)
$ 'Linear complex-to-real and real-to-complex FFT of a sequence'
WRITE(*,*)
X = RESHAPE(SOURCE = (/.1, .2, .3,0.0,0.0,0.0,7.,8.,9.,
$ 0.0, 0.0, 0.0/), SHAPE=(/6,2/))
V = X
WRITE(*,*) 'X = '
DO I = 0,N1-1
WRITE(*,'(2(F4.1,2x))') (X(I,J), J = 0, N2-1)
END DO
WRITE(*,*)
* intialize trig table and compute factors of N1
CALL SFFTCM(0, N1, N2, ONE, X, LDX, Z, LDZ, TRIGS, IFAC,
$ SW, LW, IERR)
IF (IERR .NE. 0) THEN
PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
STOP
END IF
* Compute out-of-place forward linear FFT.
* Let FFT routine allocate memory.
CALL SFFTCM(-1, N1, N2, ONE, X, LDX, Z, LDZ, TRIGS, IFAC,
$ SW, 0, IERR)
IF (IERR .NE. 0) THEN
PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
STOP
END IF
WRITE(*,*) 'out-of-place forward FFT of X:'
WRITE(*,*)'Z ='
DO I = 0, N1/2
WRITE(*,'(2(A1, F4.1,A1,F4.1,A1,2x))') ('(',REAL(Z(I,J)),
$ ',',AIMAG(Z(I,J)),')', J = 0, N2-1)
END DO
WRITE(*,*)
* Compute in-place forward linear FFT.
* X must be large enough to store N1/2+1 complex values
CALL SFFTCM(-1, N1, N2, ONE, X, LDX, X, LDC, TRIGS, IFAC,
$ SW, LW, IERR)
IF (IERR .NE. 0) THEN
PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
STOP
END IF
WRITE(*,*) 'in-place forward FFT of X:'
CALL PRINT_REAL_AS_COMPLEX(N1/2+1, N2, 1, X, LDC, N2)
WRITE(*,*)
* Compute out-of-place inverse linear FFT.
CALL CFFTSM(1, N1, N2, SCALE, Z, LDZ, X, LDX, TRIGS, IFAC,
$ SW, LW, IERR)
IF (IERR .NE. 0) THEN
PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
STOP
END IF
WRITE(*,*) 'out-of-place inverse FFT of Z:'
DO I = 0, N1-1
WRITE(*,'(2(F4.1,2X))') (X(I,J), J = 0, N2-1)
END DO
WRITE(*,*)
* Compute in-place inverse linear FFT.
CALL CFFTSM(1, N1, N2, SCALE, Z, LDZ, Z, LDZ*2, TRIGS,
$ IFAC, SW, 0, IERR)
IF (IERR .NE. 0) THEN
PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
STOP
END IF
WRITE(*,*) 'in-place inverse FFT of Z:'
CALL PRINT_COMPLEX_AS_REAL(N1, N2, 1, Z, LDZ*2, N2)
WRITE(*,*)
END PROGRAM TESTSCM
SUBROUTINE PRINT_COMPLEX_AS_REAL(N1, N2, N3, A, LD1, LD2)
INTEGER N1, N2, N3, I, J, K
REAL A(LD1, LD2, *)
DO K = 1, N3
DO I = 1, N1
WRITE(*,'(5(F4.1,2X))') (A(I,J,K), J = 1, N2)
END DO
WRITE(*,*)
END DO
END
SUBROUTINE PRINT_REAL_AS_COMPLEX(N1, N2, N3, A, LD1, LD2)
INTEGER N1, N2, N3, I, J, K
COMPLEX A(LD1, LD2, *)
DO K = 1, N3
DO I = 1, N1
WRITE(*,'(5(A1, F4.1,A1,F4.1,A1,2X))') ('(',REAL(A(I,J,K)),
$ ',',AIMAG(A(I,J,K)),')', J = 1, N2)
END DO
WRITE(*,*)
END DO
END
my_system% f95 -dalign testscm.f -xlibrary=sunperf
my_system% a.out
Linear complex-to-real and real-to-complex FFT of a sequence
X =
0.1 7.0
0.2 8.0
0.3 9.0
out-of-place forward FFT of X:
Z =
( 0.6, 0.0) (24.0, 0.0)
(-0.2, 0.1) (-1.5, 0.9)
in-place forward FFT of X:
( 0.6, 0.0) (24.0, 0.0)
(-0.2, 0.1) (-1.5, 0.9)
out-of-place inverse FFT of Z:
0.1 7.0
0.2 8.0
0.3 9.0
in-place inverse FFT of Z:
0.1 7.0
0.2 8.0
0.3 9.0
Example 7-1 Notes:
The forward FFT of X is actually:
Because of symmetry, Z(2) is the complex conjugate of Z(1), and therefore only the
first two
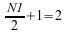 complex values are stored. For the in-place forward transform,
SFFTCM is called with real array X as the input and output.
Because SFFTCM expects the output array to be of type
COMPLEX, the leading dimension of X as an output array must
be as if X were complex. Since the leading dimension of real array X is
LDX = 2 ×
LDC, the leading dimension of X as a complex output array must be
LDC. Similarly, in the in-place inverse transform,
CFFTSM is called with complex array Z as the input and
output. Because CFFTSM expects the output array to be of type
REAL, the leading dimension of Z as an output array must be
as if Z were real. Since the leading dimension of complex array Z is
LDZ, the leading dimension of Z as a real output array must
be LDZ
× 2.
complex values are stored. For the in-place forward transform,
SFFTCM is called with real array X as the input and output.
Because SFFTCM expects the output array to be of type
COMPLEX, the leading dimension of X as an output array must
be as if X were complex. Since the leading dimension of real array X is
LDX = 2 ×
LDC, the leading dimension of X as a complex output array must be
LDC. Similarly, in the in-place inverse transform,
CFFTSM is called with complex array Z as the input and
output. Because CFFTSM expects the output array to be of type
REAL, the leading dimension of Z as an output array must be
as if Z were real. Since the leading dimension of complex array Z is
LDZ, the leading dimension of Z as a real output array must
be LDZ
× 2.
The following example Example 11 shows how to compute the linear complex-to-complex FFT of a set of sequences.
Example 11 Linear Complex-to-Complex FFTmy_system% cat testccm.f
PROGRAM TESTCCM
IMPLICIT NONE
INTEGER :: LDX1, LDY1, LW, IERR, I, J, K, LDZ1, NCPUS,
$ USING_THREADS, IFAC(128)
INTEGER, PARAMETER :: N1 = 3, N2 = 4, LDX1 = N1, LDZ1 = N1,
$ LDY1 = N1+2
REAL, PARAMETER :: ONE = 1.0, SCALE = ONE/N1
COMPLEX :: Z(0:LDZ1-1,0:N2-1), X(0:LDX1-1,0:N2-1),
$ Y(0:LDY1-1,0:N2-1)
REAL :: TRIGS(2*N1)
REAL, DIMENSION(:), ALLOCATABLE :: SW
* get number of threads
NCPUS = USING_THREADS()
* workspace size
LW = 2 * N1 * NCPUS
WRITE(*,*)'Linear complex-to-complex FFT of one or more sequences'
WRITE(*,*)
ALLOCATE(SW(LW))
X = RESHAPE(SOURCE =(/(.1,.2),(.3,.4),(.5,.6),(.7,.8),(.9,1.0),
$ (1.1,1.2),(1.3,1.4),(1.5,1.6),(1.7,1.8),(1.9,2.0),(2.1,2.2),
$ (1.2,2.0)/), SHAPE=(/LDX1,N2/))
Z = X
WRITE(*,*) 'X = '
DO I = 0, N1-1
WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))') ('(',REAL(X(I,J)),
$ ',',AIMAG(X(I,J)),')', J = 0, N2-1)
END DO
WRITE(*,*)* intialize trig table and compute factors of N1
CALL CFFTCM(0, N1, N2, SCALE, X, LDX1, Y, LDY1, TRIGS, IFAC,
$ SW, LW, IERR)
IF (IERR .NE. 0) THEN
PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
STOP
END IF
* Compute out-of-place forward linear FFT.
* Let FFT routine allocate memory.
CALL CFFTCM(-1, N1, N2, ONE, X, LDX1, Y, LDY1, TRIGS, IFAC,
$ SW, 0, IERR)
IF (IERR .NE. 0) THEN
PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
STOP
END IF
* Compute in-place forward linear FFT. LDZ1 must equal LDX1
CALL CFFTCM(-1, N1, N2, ONE, Z, LDX1, Z, LDZ1, TRIGS,
$ IFAC, SW, 0, IERR)
WRITE(*,*) 'in-place forward FFT of X:'
DO I = 0, N1-1
WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))') ('(',REAL(Z(I,J)),
$ ',',AIMAG(Z(I,J)),')', J = 0, N2-1)
END DO
WRITE(*,*)
WRITE(*,*) 'out-of-place forward FFT of X:'
WRITE(*,*) 'Y ='
DO I = 0, N1-1
WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))') ('(',REAL(Y(I,J)),
$ ',',AIMAG(Y(I,J)),')', J = 0, N2-1)
END DO
WRITE(*,*)
* Compute in-place inverse linear FFT.
CALL CFFTCM(1, N1, N2, SCALE, Y, LDY1, Y, LDY1, TRIGS, IFAC,
$ SW, LW, IERR)
IF (IERR .NE. 0) THEN
PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
STOP
END IF
WRITE(*,*) 'in-place inverse FFT of Y:'
WRITE(*,*) 'Y ='
DO I = 0, N1-1
WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))') ('(',REAL(Y(I,J)),
$ ',',AIMAG(Y(I,J)),')', J = 0, N2-1)
END DO
DEALLOCATE(SW)
END PROGRAM TESTCCM
my_system% f95 -dalign testccm.f -library=sunperf
my_system% a.out
Linear complex-to-complex FFT of one or more sequences
X =
( 0.1, 0.2) ( 0.7, 0.8) ( 1.3, 1.4) ( 1.9, 2.0)
( 0.3, 0.4) ( 0.9, 1.0) ( 1.5, 1.6) ( 2.1, 2.2)
( 0.5, 0.6) ( 1.1, 1.2) ( 1.7, 1.8) ( 1.2, 2.0)
in-place forward FFT of X:
( 0.9, 1.2) ( 2.7, 3.0) ( 4.5, 4.8) ( 5.2, 6.2)
( -0.5, -0.1) ( -0.5, -0.1) ( -0.5, -0.1) ( 0.4, -0.9)
( -0.1, -0.5) ( -0.1, -0.5) ( -0.1, -0.5) ( 0.1, 0.7)
out-of-place forward FFT of X:
Y =
( 0.9, 1.2) ( 2.7, 3.0) ( 4.5, 4.8) ( 5.2, 6.2)
( -0.5, -0.1) ( -0.5, -0.1) ( -0.5, -0.1) ( 0.4, -0.9)
( -0.1, -0.5) ( -0.1, -0.5) ( -0.1, -0.5) ( 0.1, 0.7)
in-place inverse FFT of Y:
Y =
( 0.1, 0.2) ( 0.7, 0.8) ( 1.3, 1.4) ( 1.9, 2.0)
( 0.3, 0.4) ( 0.9, 1.0) ( 1.5, 1.6) ( 2.1, 2.2)
( 0.5, 0.6) ( 1.1, 1.2) ( 1.7, 1.8) ( 1.2, 2.0)
Two-Dimensional FFT Routines
For the linear FFT routines, when the input is a two-dimensional array, the FFT is computed along one dimension only, namely, along the columns of the array. The two-dimensional FFT routines take a two-dimensional array as input and compute the FFT along both the column and row dimensions. Specifically, the forward two-dimensional FFT routines compute the following:
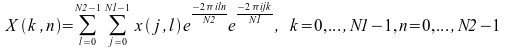
The inverse two-dimensional FFT routines compute the following:
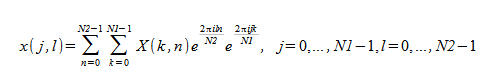
For both the forward and inverse two-dimensional transforms, a complex-to-complex transform where the input problem is N1 × N2 will yield a complex array that is also N1 × N2.
When computing a
real-to-complex two-dimensional transform (forward FFT), if the real
input array is of dimensions N1 ×
N2, the result will be a complex array of dimensions
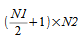 .
.
Conversely, when computing a complex-to-real transform (inverse FFT) of dimensions
N1 × N2, an
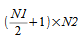 complex array is required as input. As with the real-to-complex
and complex-to-real linear FFT, because of
conjugate symmetry, only the first
complex array is required as input. As with the real-to-complex
and complex-to-real linear FFT, because of
conjugate symmetry, only the first
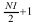 complex data points need to be stored in the input or output array
along the first dimension. The complex subarray
complex data points need to be stored in the input or output array
along the first dimension. The complex subarray
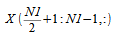 can be obtained from
can be obtained from
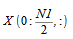 as follows:
as follows:
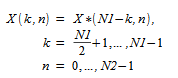
To compute a two-dimensional transform, an FFT routine must be called twice. One call initializes the routine and the second call actually computes the transform. The initialization includes computing the factors of N1 and N2 and the trigonometric weights associated with those factors. In subsequent forward or inverse transforms, initialization is not necessary as long as N1 and N2 remain unchanged.
IMPORTANT: Upon returning from a
two-dimensional FFT routine, Y(0 :
N - 1, :) contains the transform results and the original
contents of Y(N :
LDY-1, :) is overwritten. Here, N =
N1 in the complex-to-complex and complex-to-real
transforms and N =
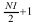 in the real-to-complex transform.
in the real-to-complex transform.
The following table Table 13 lists the single precision two-dimensional FFT routines and their purposes. The same information applies to the corresponding double precision routines except that their data types are double precision and double complex. See Table 13 for the mapping. Refer to the individual man pages for a complete description of the routines and their arguments.
| ||||||||||||||||||||||||||||||||||||||||||||||||
Note - Note the following about the table Table 13
-
LDX1 is leading dimension of input array.
-
LDY1 is leading dimension of output array.
-
N1 is first dimension of the FFT problem.
-
N2 is second dimension of the FFT problem.
-
When calling routines with OPT = 0 to initialize the routine, the only error checking that is done is to determine if N1, N2 < 0.
The following example shows how to compute a two-dimensional real-to-complex FFT and complex-to-real FFT of a two-dimensional array.
my_system% cat testsc2.f
PROGRAM TESTSC2
IMPLICIT NONE
INTEGER, PARAMETER :: N1 = 3, N2 = 4, LDX1 = N1,
$ LDY1 = N1/2+1, LDR1 = 2*(N1/2+1)
INTEGER LW, IERR, I, J, K, IFAC(128*2)
REAL, PARAMETER :: ONE = 1.0, SCALE = ONE/(N1*N2)
REAL :: V(LDR1,N2), X(LDX1, N2), Z(LDR1,N2),
$ SW(2*N2), TRIGS(2*(N1+N2))
COMPLEX :: Y(LDY1,N2)
WRITE(*,*) $'Two-dimensional complex-to-real and real-to-complex FFT'
WRITE(*,*)
X = RESHAPE(SOURCE = (/.1, .2, .3, .4, .5, .6, .7, .8,
$ 2.0,1.0, 1.1, 1.2/), SHAPE=(/LDX1,N2/))
DO I = 1, N2
V(1:N1,I) = X(1:N1,I)
END DO
WRITE(*,*) 'X ='
DO I = 1, N1
WRITE(*,'(5(F5.1,2X))') (X(I,J), J = 1, N2)
END DO
WRITE(*,*)
* Initialize trig table and get factors of N1, N2
CALL SFFTC2(0,N1,N2,ONE,X,LDX1,Y,LDY1,TRIGS,
$ IFAC,SW,0,IERR)
* Compute 2-dimensional out-of-place forward FFT.
* Let FFT routine allocate memory.
* cannot do an in-place transform in X because LDX1 < 2*(N1/2+1)
CALL SFFTC2(-1,N1,N2,ONE,X,LDX1,Y,LDY1,TRIGS,
$ IFAC,SW,0,IERR)
WRITE(*,*) 'out-of-place forward FFT of X:'
WRITE(*,*)'Y ='
DO I = 1, N1/2+1
WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))')('(',REAL(Y(I,J)),
$ ',',AIMAG(Y(I,J)),')', J = 1, N2)
END DO
WRITE(*,*)
* Compute 2-dimensional in-place forward FFT.
* Use workspace already allocated.
* V which is real array containing input data is also
* used to store complex results; as a complex array, its first
* leading dimension is LDR1/2.
CALL SFFTC2(-1,N1,N2,ONE,V,LDR1,V,LDR1/2,TRIGS,
$ IFAC,SW,LW,IERR)
WRITE(*,*) 'in-place forward FFT of X:'
CALL PRINT_REAL_AS_COMPLEX(N1/2+1, N2, 1, V, LDR1/2, N2)
* Compute 2-dimensional out-of-place inverse FFT.
* Leading dimension of Z must be even
CALL CFFTS2(1,N1,N2,SCALE,Y,LDY1,Z,LDR1,TRIGS,
$ IFAC,SW,0,IERR)
WRITE(*,*) 'out-of-place inverse FFT of Y:'
DO I = 1, N1
WRITE(*,'(5(F5.1,2X))') (Z(I,J), J = 1, N2)
END DO
WRITE(*,*)
* Compute 2-dimensional in-place inverse FFT.
* Y which is complex array containing input data is also
* used to store real results; as a real array, its first
* leading dimension is 2*LDY1.
CALL CFFTS2(1,N1,N2,SCALE,Y,LDY1,Y,2*LDY1,
$ TRIGS,IFAC,SW,0,IERR)
WRITE(*,*) 'in-place inverse FFT of Y:'
CALL PRINT_COMPLEX_AS_REAL(N1, N2, 1, Y, 2*LDY1, N2)
END PROGRAM TESTSC2
SUBROUTINE PRINT_COMPLEX_AS_REAL(N1, N2, N3, A, LD1, LD2)
INTEGER N1, N2, N3, I, J, K
REAL A(LD1, LD2, *)
DO K = 1, N3
DO I = 1, N1
WRITE(*,'(5(F5.1,2X))') (A(I,J,K), J = 1, N2)
END DO
WRITE(*,*)
END DO
END
SUBROUTINE PRINT_REAL_AS_COMPLEX(N1, N2, N3, A, LD1, LD2)
INTEGER N1, N2, N3, I, J, K
COMPLEX A(LD1, LD2, *)
DO K = 1, N3
DO I = 1, N1
WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))') ('(',REAL(A(I,J,K)),
$ ',',AIMAG(A(I,J,K)),')', J = 1, N2)
END DO
WRITE(*,*)
END DO
END
my_system% f95 -dalign testsc2.f -library=sunperf
my_system% a.out
Two-dimensional complex-to-real and real-to-complex FFT
x =
0.1 0.4 0.7 1.0
0.2 0.5 0.8 1.1
0.3 0.6 2.0 1.2
out-of-place forward FFT of X:
Y =
( 8.9, 0.0) ( -2.9, 1.8) ( -0.7, 0.0) ( -2.9, -1.8)
( -1.2, 1.3) ( 0.5, -1.0) ( -0.5, 1.0) ( 0.5, -1.0)
in-place forward FFT of X:
( 8.9, 0.0) ( -2.9, 1.8) ( -0.7, 0.0) ( -2.9, -1.8)
( -1.2, 1.3) ( 0.5, -1.0) ( -0.5, 1.0) ( 0.5, -1.0)
out-of-place inverse FFT of Y:
0.1 0.4 0.7 1.0
0.2 0.5 0.8 1.1
0.3 0.6 2.0 1.2
in-place inverse FFT of Y:
0.1 0.4 0.7 1.0
0.2 0.5 0.8 1.1
0.3 0.6 2.0 1.2
Three-Dimensional FFT Routines
Oracle Developer Studio Performance Library includes routines that compute three-dimensional FFT. In this case, the FFT is computed along all three dimensions of a three-dimensional array. The forward FFT computes
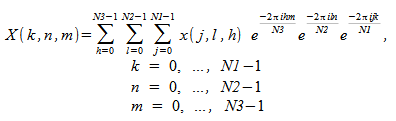 ,
,
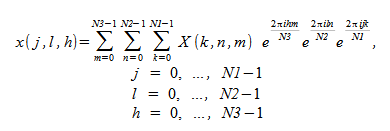
In the
complex-to-complex transform, if the input problem is
N1 ×
N2 ×
N3, a three-dimensional transform will yield a complex
array that is also N1 ×
N2 ×
N3. When computing a
real-to-complex three-dimensional transform, if the real input array is
of dimensions N1 ×
N2 ×
N3, the result will be a complex array of dimensions
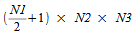 . Conversely, when computing a complex-to-real FFT of dimensions
N1 ×
N2 ×
N3, an
. Conversely, when computing a complex-to-real FFT of dimensions
N1 ×
N2 ×
N3, an
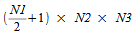 complex array is required as input. As with the real-to-complex
and complex-to-real linear FFT, because of
conjugate symmetry, only the first
complex array is required as input. As with the real-to-complex
and complex-to-real linear FFT, because of
conjugate symmetry, only the first
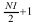 complex data points need to be stored along the first dimension.
The complex subarray
complex data points need to be stored along the first dimension.
The complex subarray
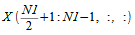 can be obtained from
can be obtained from
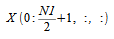 as follows:
as follows:
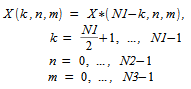
To compute a three-dimensional transform, an FFT routine must be called twice: Once to initialize and once more to actually compute the transform. The initialization includes computing the factors of N1, N2, and N3 and the trigonometric weights associated with those factors. In subsequent forward or inverse transforms, initialization is not necessary as long as N1, N2, and N3 remain unchanged.
IMPORTANT: Upon returning from a
three-dimensional FFT routine, Y(0 :
N - 1, :, :) contains the transform results and the
original contents of
Y(N:LDY1-1,
:, :) is overwritten. Here,
N=N1 in the complex-to-complex
and complex-to-real transforms and N=
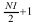 in the real-to-complex transform.
in the real-to-complex transform.
Table 14 lists the single precision three-dimensional FFT routines and their purposes. The same information applies to the corresponding double precision routines except that their data types are double precision and double complex. See Table 14 for the mapping. See the individual man pages for a complete description of the routines and their arguments.
| ||||||||||||||||||||||||||||||||||||||||||||||||
Note - Note the following about the table Table 14:
-
LDX1 is first leading dimension of input array.
-
LDX2 is the second leading dimension of the input array.
-
LDY1 is the first leading dimension of the output array.
-
LDY2 is the second leading dimension of the output array.
-
N1 is the first dimension of the FFT problem.
-
N2 is the second dimension of the FFT problem.
-
N3 is the third dimension of the FFT problem.
-
When calling routines with OPT = 0 to initialize the routine, the only error checking that is done is to determine if N1, N2, N3 < 0.
Example 7-4 shows how to compute the three-dimensional real-to-complex FFT and complex-to-real FFT of a three-dimensional array.
Example 13 Three-Dimensional Real-to-Complex FFT and Complex-to-Real FFT of a Three-Dimensional Arraymy_system% cat testsc3.f
PROGRAM TESTSC3
IMPLICIT NONE
INTEGER LW, NCPUS, IERR, I, J, K, USING_THREADS, IFAC(128*3)
INTEGER, PARAMETER :: N1 = 3, N2 = 4, N3 = 2, LDX1 = N1,
$ LDX2 = N2, LDY1 = N1/2+1, LDY2 = N2,
$ LDR1 = 2*(N1/2+1), LDR2 = N2
REAL, PARAMETER :: ONE = 1.0, SCALE = ONE/(N1*N2*N3)
REAL :: V(LDR1,LDR2,N3), X(LDX1,LDX2,N3), Z(LDR1,LDR2,N3),
$ TRIGS(2*(N1+N2+N3))
REAL, DIMENSION(:), ALLOCATABLE :: SW
COMPLEX :: Y(LDY1,LDY2,N3)
WRITE(*,*)
$'Three-dimensional complex-to-real and real-to-complex FFT'
WRITE(*,*)
* get number of threads
NCPUS = USING_THREADS()
* compute workspace size required
LW = (MAX(MAX(N1,2*N2),2*N3) + 16*N3) * NCPUS
ALLOCATE(SW(LW))
X = RESHAPE(SOURCE =
$ (/ .1, .2, .3, .4, .5, .6, .7, .8, .9,1.0,1.1,1.2,
$ 4.1,1.2,2.3,3.4,6.5,1.6,2.7,4.8,7.9,1.0,3.1,2.2/),
$ SHAPE=(/LDX1,LDX2,N3/))
V = RESHAPE(SOURCE =
$ (/.1,.2,.3,0.,.4,.5,.6,0.,.7,.8,.9,0.,1.0,1.1,1.2,0.,
$ 4.1,1.2,2.3,0.,3.4,6.5,1.6,0.,2.7,4.8,7.9,0.,
$ 1.0,3.1,2.2,0./), SHAPE=(/LDR1,LDR2,N3/))
WRITE(*,*) 'X ='
DO K = 1, N3
DO I = 1, N1
WRITE(*,'(5(F5.1,2X))') (X(I,J,K), J = 1, N2)
END DO
WRITE(*,*)
END DO
* Initialize trig table and get factors of N1, N2 and N3
CALL SFFTC3(0,N1,N2,N3,ONE,X,LDX1,LDX2,Y,LDY1,LDY2,TRIGS,
$ IFAC,SW,0,IERR)
* Compute 3-dimensional out-of-place forward FFT.
* Let FFT routine allocate memory.
* cannot do an in-place transform because LDX1 < 2*(N1/2+1)
CALL SFFTC3(-1,N1,N2,N3,ONE,X,LDX1,LDX2,Y,LDY1,LDY2,TRIGS,
$ IFAC,SW,0,IERR)
WRITE(*,*) 'out-of-place forward FFT of X:'
WRITE(*,*)'Y ='
DO K = 1, N3
DO I = 1, N1/2+1
WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))')('(',REAL(Y(I,J,K)),
$ ',',AIMAG(Y(I,J,K)),')', J = 1, N2)
END DO
WRITE(*,*)
END DO
* Compute 3-dimensional in-place forward FFT.
* Use workspace already allocated.
* V which is real array containing input data is also
* used to store complex results; as a complex array, its first
* leading dimension is LDR1/2.
CALL SFFTC3(-1,N1,N2,N3,ONE,V,LDR1,LDR2,V,LDR1/2,LDR2,TRIGS,
$ IFAC,SW,LW,IERR)
WRITE(*,*) 'in-place forward FFT of X:'
CALL PRINT_REAL_AS_COMPLEX(N1/2+1, N2, N3, V, LDR1/2, LDR2)
* Compute 3-dimensional out-of-place inverse FFT.
* First leading dimension of Z (LDR1) must be even
CALL CFFTS3(1,N1,N2,N3,SCALE,Y,LDY1,LDY2,Z,LDR1,LDR2,TRIGS,
$ IFAC,SW,0,IERR)
WRITE(*,*) 'out-of-place inverse FFT of Y:'
DO K = 1, N3
DO I = 1, N1
WRITE(*,'(5(F5.1,2X))') (Z(I,J,K), J = 1, N2)
END DO
WRITE(*,*)
END DO
* Compute 3-dimensional in-place inverse FFT.
* Y which is complex array containing input data is also
* used to store real results; as a real array, its first
* leading dimension is 2*LDY1.
CALL CFFTS3(1,N1,N2,N3,SCALE,Y,LDY1,LDY2,Y,2*LDY1,LDY2,
$ TRIGS,IFAC,SW,LW,IERR)
WRITE(*,*) 'in-place inverse FFT of Y:'
CALL PRINT_COMPLEX_AS_REAL(N1, N2, N3, Y, 2*LDY1, LDY2)
DEALLOCATE(SW)
END PROGRAM TESTSC3
SUBROUTINE PRINT_COMPLEX_AS_REAL(N1, N2, N3, A, LD1, LD2)
INTEGER N1, N2, N3, I, J, K
REAL A(LD1, LD2, *)
DO K = 1, N3
DO I = 1, N1
WRITE(*,'(5(F5.1,2X))') (A(I,J,K), J = 1, N2)
END DO
WRITE(*,*)
END DO
END
SUBROUTINE PRINT_REAL_AS_COMPLEX(N1, N2, N3, A, LD1, LD2)
INTEGER N1, N2, N3, I, J, K
COMPLEX A(LD1, LD2), *)
DO K = 1, N3
DO I = 1, N1
WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))') ('(',REAL(A(I,J,K)),
$ ',',AIMAG(A(I,J,K)),')', J = 1, N2)
END DO
WRITE(*,*)
END DO
END
my_system% f95 -dalign testsc3.f -xlibrary=sunperf
my_system% a.out
Three-dimensional complex-to-real and real-to-complex FFT
X =
0.1 0.4 0.7 1.0
0.2 0.5 0.8 1.1
0.3 0.6 0.9 1.2
4.1 3.4 2.7 1.0
1.2 6.5 4.8 3.1
2.3 1.6 7.9 2.2
out-of-place forward FFT of X:
Y =
( 48.6, 0.0) ( -9.6, -3.4) ( 3.4, 0.0) ( -9.6, 3.4)
( -4.2, -1.0) ( 2.5, -2.7) ( 1.0, 8.7) ( 9.5, -0.7)
(-33.0, 0.0) ( 6.0, 7.0) ( -7.0, 0.0) ( 6.0, -7.0)
( 3.0, 1.7) ( -2.5, 2.7) ( -1.0, -8.7) ( -9.5, 0.7)
in-place forward FFT of X:
( 48.6, 0.0) ( -9.6, -3.4) ( 3.4, 0.0) ( -9.6, 3.4)
( -4.2, -1.0) ( 2.5, -2.7) ( 1.0, 8.7) ( 9.5, -0.7)
(-33.0, 0.0) ( 6.0, 7.0) ( -7.0, 0.0) ( 6.0, -7.0)
( 3.0, 1.7) ( -2.5, 2.7) ( -1.0, -8.7) ( -9.5, 0.7)
out-of-place inverse FFT of Y:
0.1 0.4 0.7 1.0
0.2 0.5 0.8 1.1
0.3 0.6 0.9 1.2
4.1 3.4 2.7 1.0
1.2 6.5 4.8 3.1
2.3 1.6 7.9 2.2
in-place inverse FFT of Y:
0.1 0.4 0.7 1.0
0.2 0.5 0.8 1.1
0.3 0.6 0.9 1.2
4.1 3.4 2.7 1.0
1.2 6.5 4.8 3.1
2.3 1.6 7.9 2.2
Comments
When doing an in-place real-to-complex or complex-to-real transform, care must be taken to ensure the size of the input array is large enough to hold the results. For example, if the input is of type complex stored in a complex array with first leading dimension N, then to use the same array to store the real results, its first leading dimension as a real output array would be 2 × N. Conversely, if the input is of type real stored in a real array with first leading dimension 2 × N, then to use the same array to store the complex results, its first leading dimension as a complex output array would be N. Leading dimension requirements for in-place and out-of-place transforms can be found in Table 12, Table 13, and Table 14.
In the linear and multi-dimensional FFT, the transform between real and complex data through a
real-to-complex or complex-to-real transform can be confusing because
N1 real data points correspond to
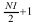 complex data points. N1 real data
points do map to N1 complex data points, but because
there is conjugate symmetry in the complex data, only
complex data points. N1 real data
points do map to N1 complex data points, but because
there is conjugate symmetry in the complex data, only
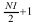 data points need to be stored as input in the complex-to-real
transform and as output in the real-to-complex transform. In the multi-dimensional
FFT, symmetry exists along all the dimensions, not just in the first. However, the
two-dimensional and three-dimensional FFT routines store the complex data of the
second and third dimensions in their entirety.
data points need to be stored as input in the complex-to-real
transform and as output in the real-to-complex transform. In the multi-dimensional
FFT, symmetry exists along all the dimensions, not just in the first. However, the
two-dimensional and three-dimensional FFT routines store the complex data of the
second and third dimensions in their entirety.
While the FFT routines accept any size of N1, N2 and N3, FFTs can be computed most efficiently when values of N1, N2 and N3 can be decomposed into relatively small primes. A real-to-complex or a complex-to-real transform can be computed most efficiently when
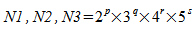 ,
,
and a complex-to-complex transform can be computed most efficiently when
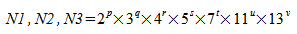 ,
,
where p, q, r, s, t, u, and v are integers and p, q, r, s, t, u, v ≥ 0.
The function xFFTOPT can be used to determine the optimal sequence length, as shown in Example 14. Given an input sequence length, the function returns an optimal length that is closest in size to the original length.
Example 14 RFFTOPT Examplemy_system% cat fft_ex01.f
PROGRAM TEST
INTEGER N, N1, N2, N3, RFFTOPT
C
N = 1024
N1 = 1019
N2 = 71
N3 = 49
C
PRINT *, 'N Original N Suggested'
PRINT '(I5, I12)', (N, RFFTOPT(N))
PRINT '(I5, I12', (N1, RFFTOPT(N1))
PRINT '(I5, I12)', (N2, RFFTOPT(N2))
PRINT '(I5, I12)', (N3, RFFTOPT(N3))
END
my_system% f95 -dalign fft_ex01.f -library=sunperf
my_system% a.out
N Original N Suggested
1024 1024
1019 1024
71 72
49 49
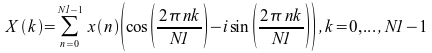 .
.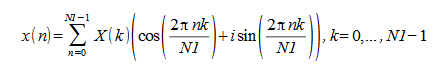
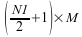 ,
,