Convolution and Correlation

Two applications of the FFT that are frequently encountered especially in the signal processing area are the discrete convolution and discrete correlation operations.

Convolution Operation

Given two functions x(t) and y(t), the Fourier transform of the convolution of x(t) and y(t), denoted as x * y, is the product of their individual Fourier transforms: DFT (x * y)=X (•) Y where * denotes the convolution operation and (•) denotes pointwise multiplication.

Typically, x(t) is a continuous and periodic signal that is represented discretely by a set of N data points x_j, j = 0, …, N -1, sampled over a finite duration, usually for one period of x(t) at equal intervals. y(t) is usually a response that starts out as zero, peaks to a maximum value, and then returns to zero. Discretizing y(t) at equal intervals produces a set of N data points, y_k, k = 0, …, N -1. If the actual number of samplings in y_k is less than N, the data can be padded with zeros. The discrete convolution can then be defined as

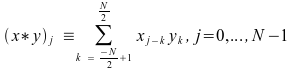
The values of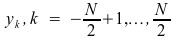

are the same as those of k = 0, …, N -1 but in the wrap-around order.

The Oracle Developer Studio Performance Library routines enable you to compute the convolution by using the definition above with k = 0, …, N -1, or by using the FFT. If the FFT is used to compute the convolution of two sequences, the following steps are performed:

• Compute X = forward FFT of x

• Compute Y = forward FFT of y

• Compute Z = X (•) Y <=> DFT (x * y)

• Compute z = inverse FFT of Z; z = (x * y)

One interesting characteristic of convolution is that the product of two polynomials is actually a convolution. A product of an m-term polynomial

and an n-term polynomial

has m+n-1 coefficients that can be obtained by:

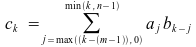
where k = 0, …, m + n - 2.

Correlation Operation

Closely related to convolution is the correlation operation. It computes the correlation of two sequences directly superposed or when one is shifted relative to the other. As with convolution, we can compute the correlation of two sequences efficiently as follows using the FFT:

• Compute the FFT of the two input sequences.

• Compute the pointwise product of the resulting transform of one sequence and the complex conjugate of the transform of the other sequence.

• Compute the inverse FFT of the product.

The routines in the Performance Library also allow correlation to be computed by the following definition:

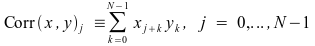
There are various ways to interpret the sampled input data of the convolution and correlation operations. The argument list of the convolution and correlation routines contain parameters to handle the following cases:

• The signal and/or response function can start at different sampling times.

• You might want only part of the signal to contribute to the output.

• The signal and/or response function can begin with one or more zeros that are not explicitly stored.

Oracle Developer Studio Performance Library Convolution and Correlation Routines

Oracle Developer Studio Performance Library contains the convolution routines shown in Table 19.

Table 19  Convolution and Correlation Routines

Routine Arguments Function SCNVCOR, DCNVCOR, CCNVCOR, ZCNVCOR CNVCOR,FOUR,NX,X,IFX, INCX,NY,NPRE,M,Y,IFY, INC1Y,INC2Y,NZ,K,Z, IFZ,INC1Z,INC2Z,WORK, LWORK Convolution or correlation of a filter with one or more vectors SCNVCOR2, DCNVCOR2, CCNVCOR2, ZCNVCOR2 CNVCOR,METHOD,TRANSX, SCRATCHX,TRANSY, SCRATCHY,MX,NX,X,LDX, MY,NY,MPRE,NPRE,Y,LDY, MZ,NZ,Z,LDZ,WORKIN, LWORK Two-dimensional convolution or correlation of two matrices SWIENER, DWIENER N_POINTS,ACOR,XCOR, FLTR,EROP,ISW,IERR Wiener deconvolution of two signals

The [S,D,C,Z]CNVCOR routines are used to compute the convolution or correlation of a filter with one or more input vectors. The [S,D,C,Z]CNVCOR2 routines are used to compute the two-dimensional convolution or correlation of two matrices.

Arguments for Convolution and Correlation Routines

The one-dimensional convolution and correlation routines use the arguments shown in Table 20.

Table 20  Arguments for One-Dimensional Convolution and Correlation Routines SCNVCOR, DCNVCOR, CCNVCOR, and ZCNVCOR

Argument Definition CNVCOR 'V' or 'v' specifies that convolution is computed. 'R' or 'r' specifies that correlation is computed. FOUR 'T' or 't' specifies that the Fourier transform method is used. 'D' or 'd' specifies that the direct method is used, where the convolution or correlation is computed from the definition of convolution and correlation. When the lengths of the two sequences to be convolved are similar, the FFT method is faster than the direct method. However, when one sequence is much larger than the other, such as when convolving a large time-series signal with a small filter, the direct method performs faster than the FFT-based method. NX Length of filter vector, where NX≥ 0. X Filter vector IFX Index of first element of X, where NX ≥ IFX ≥ 1 INCX Stride between elements of the vector in X, where INCX > 0. NY Length of input vectors, where NY ≥ 0. NPRE Number of implicit zeros prefixed to the Y vectors, where NPRE ≥ 0. M Number of input vectors, where M ≥ 0. Y Input vectors. IFY Index of the first element of Y, where NY ≥ IFY ≥ 1 INC1Y Stride between elements of the input vectors in Y, where INC1Y > 0. INC2Y Stride between input vectors in Y, where INC2Y > 0. NZ Length of the output vectors, where NZ ≥ 0. K Number of Z vectors, where K ≥ 0. If K < M, only the first K vectors will be processed. If K > M, all input vectors will be processed and the last M-K output vectors will be set to zero on exit. Z Result vectors IFZ Index of the first element of Z, where NZ ≥ IFZ ≥ 1 INC1Z Stride between elements of the output vectors in Z, where INCYZ > 0. INC2Z Stride between output vectors in Z, where INC2Z > 0. WORK Work array LWORK Length of work array

The two-dimensional convolution and correlation routines use the arguments shown in Table 21.

Table 21  Arguments for Two-Dimensional Convolution and Correlation Routines SCNVCOR2, DCNVCOR2, CCNVCOR2, and ZCNVCOR2

Argument Definition CNVCOR 'V' or 'v' specifies that convolution is computed. 'R' or 'r' specifies that correlation is computed. METHOD 'T' or 't' specifies that the Fourier transform method is used. 'D' or 'd' specifies that the direct method is used, where the convolution or correlation is computed from the definition of convolution and correlation. When the sizes of the two matrices to be convolved are similar, the FFT method is faster than the direct method. However, when one sequence is much larger than the other, such as when convolving a large data set with a small filter, the direct method performs faster than the FFT-based method. TRANSX 'N' or 'n' specifies that X is the filter matrix 'T' or 't' specifies that the transpose of X is the filter matrix SCRATCHX 'N' or 'n' specifies that X must be preserved 'S' or 's' specifies that X can be used for scratch space. The contents of X are undefined after returning from a call where X is used for scratch space. TRANSY 'N' or 'n' specifies that Y is the input matrix 'T' or 't' specifies that the transpose of Y is the input matrix SCRATCHY 'N' or 'n' specifies that Y must be preserved 'S' or 's' specifies that Y can be used for scratch space. The contents of X are undefined after returning from a call where Y is used for scratch space. MX Number of rows in the filter matrix X, where MX ≥ 0 NX Number of columns in the filter matrix X, where NX ≥ 0 X Filter matrix. X is unchanged on exit when SCRATCHX is 'N' or 'n' and undefined on exit when SCRATCHX is 'S' or 's'. LDX Leading dimension of array containing the filter matrix X. MY Number of rows in the input matrix Y, where MY ≥ 0. NY Number of columns in the input matrix Y, where NY ≥ 0 MPRE Number of implicit zeros prefixed to each row of the input matrix Y vectors, where MPRE ≥ 0. NPRE Number of implicit zeros prefixed to each column of the input matrix Y, where NPRE ≥ 0. Y Input matrix. Y is unchanged on exit when SCRATCHY is 'N' or 'n' and undefined on exit when SCRATCHY is 'S' or 's'. LDY Leading dimension of array containing the input matrix Y. MZ Number of output vectors, where MZ ≥ 0. NZ Length of output vectors, where NZ ≥ 0. Z Result vectors LDZ Leading dimension of the array containing the result matrix Z, where LDZ ≥ MAX(1,MZ). WORKIN Work array LWORK Length of work array

Work Array WORK for Convolution and Correlation Routines

The minimum dimensions for the WORK work arrays used with the one-dimensional and two-dimensional convolution and correlation routines are shown in Table 24. The minimum dimensions for one-dimensional convolution and correlation routines depend upon the values of the arguments NPRE, NX, NY, and NZ.

The minimum dimensions for two-dimensional convolution and correlation routines depend upon the values of the arguments shown in the table Table 22.

Table 22  Arguments Affecting Minimum Work Array Size for Two-Dimensional Routines: SCNVCOR2, DCNVCOR2, CCNVCOR2, and ZCNVCOR2

Argument Definition MX Number of rows in the filter matrix MY Number of rows in the input matrix MZ Number of output vectors NX Number of columns in the filter matrix NY Number of columns in the input matrix NZ Length of output vectors MPRE Number of implicit zeros prefixed to each row of the input matrix NPRE Number of implicit zeros prefixed to each column of the input matrix MPOST MAX(0,MZ-MYC) NPOST MAX(0,NZ-NYC) MYC MPRE + MPOST + MYC_INIT, where MYC_INIT depends upon filter and input matrices, as shown in Table 23 NYC NPRE + NPOST + NYC_INIT, where NYC_INIT depends upon filter and input matrices, as shown in Table 23

MYC_INIT and NYC_INIT depend upon the following, where X is the filter matrix and Y is the input matrix.

Table 23  MYC_INIT and NYC_INIT Dependencies

Routine Y Transpose(Y) X Transpose(X) X Transpose(X) MYC_INIT MAX(MX,MY) MAX(NX,MY) MAX(MX,NY) MAX(NX,NY) NYC_INIT MAX(NX,NY) MAX(MX,NY) MAX(NX,MY) MAX(MX,MY)

The values assigned to the minimum work array size is shown in Table 24.

Table 24  Minimum Dimensions and Data Types for WORK Work Array Used With Convolution and Correlation Routines

Routine Minimum Work Array Size (WORK) Type SCNVCOR, DCNVCOR 4*(MAX(NX,NPRE+NY) + MAX(0,NZ-NY)) REAL, REAL*8 CCNVCOR, ZCNVCOR 2*(MAX(NX,NPRE+NY) + MAX(0,NZ‐NY))) COMPLEX, COMPLEX*16 SCNVCOR2†, DCNVCOR2† MY + NY + 30 COMPLEX, COMPLEX*16 CCNVCOR2†, ZCNVCOR2† If MY = NY: MYC + 8 If MY ≥ NY: MYC + NYC + 16 COMPLEX, COMPLEX*16

Memory will be allocated within the routine if the workspace size, indicated by LWORK, is not large enough.

Sample Program: Convolution

The following example uses CCNVCOR to perform FFT convolution of two complex vectors.

Example 19  One-Dimensional Convolution Using Fourier Transform Method and COMPLEX Data

my_system% cat con_ex20.f
      PROGRAM TEST
C
      INTEGER           LWORK
      INTEGER           N
      PARAMETER        (N = 3)
      PARAMETER        (LWORK = 4 * N + 15)
      COMPLEX           P1(N), P2(N), P3(2*N-1), WORK(LWORK)
      DATA P1 / 1, 2, 3 /,  P2 / 4, 5, 6 /
C
      EXTERNAL          CCNVCOR
C
      PRINT *, 'P1:'
      PRINT 1000, P1
      PRINT *, 'P2:'
      PRINT 1000, P2
 
      CALL CCNVCOR ('V', 'T', N, P1, 1, 1, N, 0, 1, P2, 1, 1, 1,
     $              2 * N - 1, 1, P3, 1, 1, 1, WORK, LWORK)
C
      PRINT *, 'P3:'
      PRINT 1000, P3
C
 1000 FORMAT (1X, 100(F4.1,' +',F4.1,'i  '))
C
      END
my_system% f95 -dalign con_ex20.f -xlibrary=sunperf
my_system% a.out
 P1:
  1.0 + 0.0i   2.0 + 0.0i   3.0 + 0.0i  
 P2:
  4.0 + 0.0i   5.0 + 0.0i   6.0 + 0.0i  
 P3:
  4.0 + 0.0i  13.0 + 0.0i  28.0 + 0.0i  27.0 + 0.0i  18.0 + 0.0i 

If any vector overlaps a writable vector, either because of argument aliasing or ill-chosen values of the various INC arguments, the results are undefined and can vary from one run to the next.

The most common form of the computation, and the case that executes fastest, is applying a filter vector X to a series of vectors stored in the columns of Y with the result placed into the columns of Z. In that case, INCX = 1, INC1Y = 1, INC2Y ≥ NY, INC1Z = 1, INC2Z ≥ NZ. Another common form is applying a filter vector X to a series of vectors stored in the rows of Y and store the result in the row of Z, in which case INCX = 1, INC1Y ≥ NY, INC2Y = 1, INC1Z ≥ NZ, and INC2Z = 1.

Convolution can be used to compute the products of polynomials. The following example Example 20 uses SCNVCOR to compute the product of 1 + 2x + 3x² and 4 + 5x + 6x².

Example 20  One-Dimensional Convolution Using Fourier Transform Method and REAL Data

my_system% cat con_ex21.f
      PROGRAM TEST
      INTEGER     LWORK, NX, NY, NZ
      PARAMETER  (NX = 3)
      PARAMETER  (NY = NX)
      PARAMETER  (NZ = 2*NY-1)
      PARAMETER  (LWORK = 4*NZ+32)
      REAL        X(NX), Y(NY), Z(NZ), WORK(LWORK)
C
      DATA X / 1, 2, 3 /,  Y / 4, 5, 6 /, WORK / LWORK*0 /
C
      PRINT 1000, 'X'
      PRINT 1010, X
      PRINT 1000, 'Y'
      PRINT 1010, Y
      CALL SCNVCOR ('V', 'T', NX, X, 1, 1,   
     $NY, 0, 1, Y, 1, 1, 1,   NZ, 1, Z, 1, 1, 1, WORK, LWORK)
      PRINT 1020, 'Z'
      PRINT 1010, Z
 1000 FORMAT (1X, 'Input vector ', A1)
 1010 FORMAT (1X, 300F5.0)
 1020 FORMAT (1X, 'Output vector ', A1)
      END
my_system% f95 -dalign con_ex21.f -library=sunperf
my_system% a.out
 Input vector X
    1.   2.   3.
 Input vector Y
    4.   5.   6.
 Output vector Z
    4.  13.  28.  27.  18.

Making the output vector longer than the input vectors, as in the example above, implicitly adds zeros to the end of the input. No zeros are actually required in any of the vectors, and none are used in the example, but the padding provided by the implied zeros has the effect of an end-off shift rather than an end-around shift of the input vectors.

The following example Example 21 computes the product between the vector [ 1, 2, 3 ] and the circulant matrix defined by the initial column vector [ 4, 5, 6 ].

Example 21  Convolution Used to Compute the Product of a Vector and Circulant Matrix

my_system% cat con_ex22.f 
      PROGRAM TEST
C
      INTEGER     LWORK, NX, NY, NZ
      PARAMETER  (NX = 3)
      PARAMETER  (NY = NX)
      PARAMETER  (NZ = NY)
      PARAMETER  (LWORK = 4*NZ+32)
      REAL        X(NX), Y(NY), Z(NZ), WORK(LWORK)
C
      DATA X / 1, 2, 3 /,  Y / 4, 5, 6 /, WORK / LWORK*0 /
C
      PRINT 1000, 'X'
      PRINT 1010, X
      PRINT 1000, 'Y'
      PRINT 1010, Y
      CALL SCNVCOR ('V', 'T', NX, X, 1, 1,   
     $NY, 0, 1, Y, 1, 1, 1,   NZ, 1, Z, 1, 1, 1, 
     $WORK, LWORK)
      PRINT 1020, 'Z'
      PRINT 1010, Z
C
 1000 FORMAT (1X, 'Input vector ', A1)
 1010 FORMAT (1X, 300F5.0)
 1020 FORMAT (1X, 'Output vector ', A1)
      END
my_system% f95 -dalign con_ex22.f -library=sunperf
my_system% a.out
 Input vector X
    1.   2.   3.
 Input vector Y
    4.   5.   6.
 Output vector Z
   31.  31.  28.

The difference between the following example and the previous example is that the length of the output vector is the same as the length of the input vectors, so there are no implied zeros on the end of the input vectors. With no implied zeros to shift into, the effect of an end-off shift from the previous example does not occur and the end-around shift results in a circulant matrix product.

Example 22  Two-Dimensional Convolution Using Direct Method

my_system% cat con_ex23.f
      PROGRAM TEST
C
      INTEGER           M, N
      PARAMETER        (M = 2)
      PARAMETER        (N = 3)
C
      INTEGER           I, J
      COMPLEX           P1(M,N), P2(M,N), P3(M,N)
      DATA P1 / 1, -2, 3, -4, 5, -6 /,  P2 / -1, 2, -3, 4, -5, 6 /
      EXTERNAL          CCNVCOR2
C
      PRINT *, 'P1:'
      PRINT 1000, ((P1(I,J), J = 1, N), I = 1, M)
      PRINT *, 'P2:'
      PRINT 1000, ((P2(I,J), J = 1, N), I = 1, M)
C
      CALL CCNVCOR2 ('V', 'Direct', 'No Transpose X', 'No Overwrite X',
     $   'No Transpose Y', 'No Overwrite Y', M, N, P1, M,
     $   M, N, 0, 0, P2, M, M, N, P3, M, 0, 0)
C
      PRINT *, 'P3:'
      PRINT 1000, ((P3(I,J), J = 1, N), I = 1, M)
C
 1000 FORMAT (3(F5.1,' +',F5.1,'i  '))
C
      END
my_system% f95 -dalign con_ex23.f -library=sunperf
my_system% a.out
 P1:
  1.0 +  0.0i    3.0 +  0.0i    5.0 +  0.0i  
 -2.0 +  0.0i   -4.0 +  0.0i   -6.0 +  0.0i  
 P2:
 -1.0 +  0.0i   -3.0 +  0.0i   -5.0 +  0.0i  
  2.0 +  0.0i    4.0 +  0.0i    6.0 +  0.0i  
 P3:
-83.0 +  0.0i  -83.0 +  0.0i  -59.0 +  0.0i  
 80.0 +  0.0i   80.0 +  0.0i   56.0 +  0.0i