23 Creating ADF Databound Tables
This chapter describes how to use the Data Controls panel to create data bound tables using ADF Faces components.
This chapter includes the following sections:
23.1 Introduction to Adding Tables
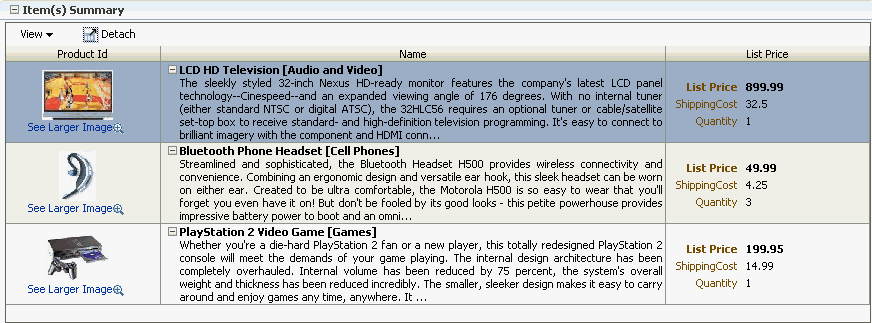
Unlike forms, tables allow you to display more than one data object from a collection at a time. Figure 23-1 shows the Items Ordered tab of the My Orders page in the StoreFront module application, which uses a browse table to display the items for a given order.
You can create tables that simply display data, or you can create tables that allow you to edit or create data. Once you drop a collection as a table, you can add command buttons bound to actions that execute some logic on a selected row. You can also modify the default components to suit your needs.
23.2 Creating a Basic Table
Unlike with forms where you bind the individual UI components that make up a form to the individual attributes on the collection, with a table you bind the ADF Faces table component to the complete collection or to a range of n data objects at a time from the collection. The individual components used to display the data in the columns are then bound to the attributes. The iterator binding handles displaying the correct data for each object, while the table component handles displaying each object in a row. JDeveloper allows you to do this declaratively, so that you don't need to write any code.
23.2.1 How to Create a Basic Table
To create a table using a data control, you bind the table component to a collection. JDeveloper allows you to do this declaratively by dragging and dropping a collection from the Data Controls panel.
Tip:
You can also create a table by dragging a table component from the Component Palette and completing the Create ADF Faces Table wizard.-
From the Data Controls panel, select a collection.
For example, to create a simple table in the StoreFront module that displays products in the system, you would select the
Productscollection. -
Drag the collection onto a JSF page, and from the context menu, choose the appropriate table.
When you drag the collection, you can choose from the following types of tables:
-
ADF Table: Allows you to select the specific attributes you wish your editable table columns to display, and what UI components to use to display the data. By default, ADF
inputTextcomponents are used for most attributes, thus enabling the table to be editable. Attributes that are dates use theinputDatecomponent. Additionally, if a control type control hint has been created for an attribute, or if the attribute has been configured to be a list, then the component set by the hint is used instead. -
ADF Read-Only Table: Same as the ADF Table; however, each attribute is displayed in an
outputTextcomponent. -
ADF Read-Only Dynamic Table: Allows you to create a table when the attributes returned and displayed are determined dynamically at runtime. This component is helpful when the attributes for the corresponding object are not known until runtime, or you do not wish to hardcode the column names in the JSF page.
-
-
The ensuing Edit Table Columns dialog shows each attribute in the collection, and allows you to determine how these attributes will behave and appear as columns in your table.
Note:
If the collection contains a structured attribute (an attribute that is neither a Java primitive type nor a collection), the attributes of the structured attributes will also appear in the dialog.Using this dialog, you can do the following:
-
Allow the ADF Model layer to handle selection by selecting the Row Selection checkbox. Selecting this option means that the iterator binding will access the iterator to determine the selected row. Select this option unless you do not want the table to allow selection.
-
Allow the ADF Model layer to handle column sorting by selecting the Sorting checkbox. Selecting this option means that the iterator binding will access the iterator, which will perform an order-by query to determine the order. Select this option unless you do not want to allow column sorting.
-
Allow the columns in the table to be filtered using entered criteria by selecting the Filtering checkbox. Selecting this option allows the user to enter criteria in text fields above each column. That criteria is then used to build a Query-by-Example (QBE) search on the collection, so that the table will display only the results returned by the query. For more information, see Section 27.5, "Creating Standalone Filtered Search Tables from Named View Criteria."
-
Group columns for selected attributes together under a parent column, by selecting the desired attributes (shown as rows in the dialog), and clicking the Group button. Figure 23-2 shows how three grouped columns appear in the visual editor after the table is created.
-
Change the display label for a column. By default, the label is bound to the
labelsproperty for any control hint defined for the attribute on the table binding. This binding allows you to change the value of a label text once on the view object, and have the change appear the same on all pages that display the label.Instead of using this default, you can enter text or an EL expression to bind the label value to something else, for example, a key in a resource file.
-
Change the value binding for a column. You can change the column to be bound to a different attribute. If you simply want to rearrange the columns, you should use the order buttons. If you do change the attribute binding for a column, the label for the column also changes.
-
Change the UI component used to display an attribute. The UI components are set based on the table you selected when you dropped the collection onto the page, on the type of the corresponding attribute (for example,
inputDatecomponents are used for attributes that are dates), and on whether or not default components were set as control hints on the corresponding view object. You can change to another component using the dropdown menu.Tip:
If one of the attributes for your table is also a primary key, you may want to choose a UI component that will not allow a user to change the value.Tip:
If you want to use a component that is not listed in the dropdown menu, use this dialog to select theoutputTextcomponent, and then manually add the other tag to the page. -
Change the order of the columns using the order buttons.
-
Add a column using the Add icon. There's no limit to the number of columns you can add. When you first click the icon, JDeveloper adds a new column line at the bottom of the dialog and populates it with the values from the first attribute in the bound collection; subsequent new columns are populated with values from the next attribute in the sequence, and so on.
-
Delete a column using the Delete icon.
-
-
Once the table is dropped on the page, you can use the Property Inspector to set other display properties of the table. For example, you may want to set the width of the table to a certain percentage or size.For more information about display properties, see the "Using Tables and Trees" chapter of the Oracle Fusion Middleware Web User Interface Developer's Guide for Oracle Application Development Framework.
Tip:
When you set the table width to 100%, the table will not include borders, so the actual width of the table will be larger. To have the table set to 100% of the container width, expand the Style section of the Property Inspector, select the Box tab, and set theBorder Widthattribute to 0 pixels. -
If you want the user to be able to edit information in the table and save any changes, you need to provide a way to submit and persist those changes. For more information, see Section 23.3, "Creating an Editable Table." For procedures on creating tables that allow users to input data, see Section 23.4, "Creating an Input Table."
23.2.2 What Happens When You Create a Table
Dropping a table from the Data Controls panel has the same effect as dropping a text field or form. Briefly, JDeveloper does the following:
-
Creates the bindings for the table and adds the bindings to the page definition file
-
Adds the necessary code for the UI components to the JSF page
For more information, see Section 22.2.2, "What Happens When You Create a Text Field."
23.2.2.1 Iterator and Value Bindings for Tables
When you drop a table from the Data Controls panel, a tree value binding is created. A tree consists of a hierarchy of nodes, where each subnode is a branch off a higher level node. In the case of a table, it is a flattened hierarchy, where each attribute (column) is a subnode off the table. Like an attribute binding used in forms, the tree value binding references the iterator binding, while the iterator binding references an iterator for the data collection, which facilitates iterating over the data objects in the collection. Instead of creating a separate binding for each attribute, only the tree binding to the table node is created. In the tree binding, the AttrNames element within the nodeDefinition element contains a child element for each attribute that you want to be available for display or reference in each row of the table.
The tree value binding is an instance of the FacesCtrlHierBinding class that extends the core JUCtrlHierBinding class to add two JSF specific properties: collectionModel.
-
collectionModel: Returns the data wrapped by an object that extends thejavax.faces.model.DataModelobject that JSF and ADF Faces use for collection-valued components like tables. -
treeModel: ExtendscollectionModelto return data that is hierarchical in nature. For more information, see Chapter 24, "Displaying Master-Detail Data."
Example 23-1 shows the value binding for the table created when you drop the Products collection.
Example 23-1 Value Binding Entries for a Table in the Page Definition File
<bindings>
<tree IterBinding="ProductsIterator" id="Products">
<nodeDefinition DefName="oracle.fodemo.storefront.store.queries.ProductsVO">
<AttrNames>
<Item Value="ProductId"/>
<Item Value="SupplierId"/>
<Item Value="CategoryId"/>
<Item Value="ProductName"/>
<Item Value="CostPrice"/>
<Item Value="ListPrice"/>
.
.
.
</AttrNames>
</nodeDefinition>
</tree>
</bindings>
Only the table component needs to be bound to the model (as opposed to the columns or the text components within the individual cells), because only the table needs access to the data. The tree binding for the table drills down to the individual structure attributes in the table, and the table columns can then derive their information from the table component.
23.2.2.2 Code on the JSF Page for an ADF Faces Table
When you use the Data Controls panel to drop a table onto a JSF page, JDeveloper inserts an ADF Faces table component, which contains an ADF Faces column component for each attribute named in the table binding. Each column then contains another component (such as an inputText or outputText component) bound to the attribute's value. Each column's heading is bound to the labels property for the control hint of the attribute.
Tip:
If an attribute is marked as hidden on the associated view or entity object, no corresponding UI is created for it.Example 23-2 shows a simplified code excerpt from a table created by dropping the Products collection as a read only table.
Example 23-2 Simplified JSF Code for an ADF Faces Table
<af:table value="#{bindings.Products.collectionModel}" var="row"
rows="#{bindings.Products.rangeSize}"
emptyText="#{bindings.Products.viewable ? 'No data to display.':
'Access Denied.'}"
fetchSize="#{bindings.Products.rangeSize}"
selectedRowKeys="#{bindings.Products.collectionModel.selectedRow}"
selectionListener="#{bindings.Products.collectionModel.makeCurrent}"
rowSelection="single" id="t1">
<af:column sortProperty="ProductId" sortable="true"
headerText="#{bindings.Products.hints.ProductId.label}" id="c1">
<af:outputText value="#{row.ProductId}" id="ot1"/>
</af:column>
<af:column sortProperty="SupplierId" sortable="true"
headerText="#{bindings.Products.hints.SupplierId.label}" id="c2">
<af:outputText value="#{row.SupplierId}" id="ot2">
<af:convertNumber groupingUsed="false"
pattern="#{bindings.Products.hints.SupplierId.format}"/>
</af:outputText>
</af:column>
<af:column sortProperty="CostPrice" sortable="true"
headerText="#{bindings.Products.hints.CostPrice.label}" id="c3">
<af:outputText value="#{row.CostPrice}" id="ot3">
<af:convertNumber groupingUsed="false"
pattern="#{bindings.Products.hints.CostPrice.format}"/>
</af:outputText>
</af:column>
.
.
.
</af:table>
The tree binding iterates over the data exposed by the iterator binding. Note that the table's value is bound to the collectionModel property, which accesses the collectionModel object. The table wraps the result set from the iterator binding in a collectionModel object. The collectionModel allows each item in the collection to be available within the table component using the var attribute.
In the example, the table iterates over the rows in the current range of the Products iterator binding. The iterator binding binds to a row set iterator that keeps track of the current row. When you set the var attribute on the table to row, each column then accesses the current data object for the current row presented to the table tag using the row variable, as shown for the value of the af:outputText tag:
<af:outputText value="#{row.ProductId}"/>
When you drop an ADF Table (as opposed to an ADF Read Only Table), instead of being bound to the row variable, the value of the input component is implicitly bound to a specific row in the binding container through the bindings property, as shown in Example 23-3. Additionally, JDeveloper adds validator and converter components for each input component. By using the bindings property, any raised exception can be linked to the corresponding binding object or objects. The controller iterates through all exceptions in the binding container and retrieves the binding object to get the client ID when creating FacesMessage objects. This retrieval allows the table to display errors for specific cells. This strategy is used for all input components, including selection components such as lists.
Example 23-3 Using Input Components Adds Validators and Converters
<af:table value="#{bindings.Products.collectionModel}" var="row"
rows="#{bindings.Products.rangeSize}"
first="#{bindings.Products.rangeStart}"
emptyText="#{bindings.Products.viewable ? 'No data to display.':
'Access Denied.'}"
fetchSize="#{bindings.Products.rangeSize}"
selectedRowKeys="#{bindings.Products.collectionModel.selectedRow}"
selectionListener="#{bindings.Products.collectionModel.makeCurrent}"
rowSelection="single" id="t1">
<af:column sortProperty="ProductId" sortable="true"
headerText="#{bindings.Products.hints.ProductId.label}" id="c1">
<af:inputText value="#{row.bindings.ProductId.inputValue}" id="it1"
<f:validator binding="#{row.bindings.ProductId.validator}"/>
<af:convertNumber groupingUsed="false"
pattern="#{bindings.Products.hints.ProductId.format}"/>
</af:inputText>
</af:column>
For more information about using ADF Faces validators and converters, see the "Validating and Converting Input" chapter of the Oracle Fusion Middleware Web User Interface Developer's Guide for Oracle Application Development Framework.
Table 23-1 shows the other attributes defined by default for ADF Faces tables created using the Data Controls panel.
Table 23-1 ADF Faces Table Attributes and Populated Values
| Attribute | Description | Default Value |
|---|---|---|
|
|
Determines how many rows to display at one time. |
An EL expression that, by default, evaluates to the |
|
|
Index of the first row in a range (based on 0). |
An EL expression that evaluates to the |
|
|
Text to display when there are no rows to return. |
An EL expression that evaluates to the viewable property on the iterator. If the table is viewable, the attribute displays No data to display when no objects are returned. If the table is not viewable (for example, if there are authorization restrictions set against the table), it displays Access Denied. |
|
|
Number of rows of data fetched from the data source. |
An EL expression that, by default, evaluates to the Note that to improve scrolling behavior in a table, when the table's iterator binding is expected to manage a data set consisting of over 200 items, and the view object is configured to use range paging, the iterator actually returns a set of ranges instead of just one range. For more information about using range paging, see Section 39.1.5, "Efficiently Scrolling Through Large Result Sets Using Range Paging." |
|
|
The selection state for the table. |
An EL expression that by default, evaluates to the selected row on the collection model. |
|
Reference to a method that listens for a selection event. |
An EL expression that by default, evaluates to the |
|
|
|
Determines whether rows are selectable. |
Set to |
|
Column Attributes |
||
|
|
Determines the property on which to sort the column. |
Set to the columns corresponding attribute binding value. |
|
|
Determines whether a column can be sorted. |
Set to |
|
|
Determines the text displayed at the top of the column. |
An EL expression that, by default, evaluates to the label control hint set on the corresponding attribute. |
23.2.3 What You May Need to Know About Setting the Current Row in a Table
When you use tables in an application and you allow the ADF Model layer to manage row selection, the current row is determined by the iterator. When a user selects a row in an ADF Faces table, the row in the table is shaded, and the component notifies the iterator of the selected row. To do this, the selectedRowKeys attribute of the table is bound to the collection model's selected row, as shown in Example 23-4.
Example 23-4 Selection Attributes on a Table
<af:table value="#{bindings.Products1.collectionModel}" var="row"
.
.
.
selectedRowKeys="#{bindings.Products.collectionModel.selectedRow}"
selectionListener="#{bindings.Products.collectionModel.
makeCurrent}"
rowSelection="single">
This binding binds the selected keys in the table to the selected row of the collection model. The selectionListener attribute is then bound to the collection model's makeCurrent property. This binding makes the selected row of the collection the current row of the iterator.
Note:
If you create a custom selection listener, you must create a method binding to themakeCurrent property on the collection model (for example #{binding.Products.collectionModel.makeCurrent}) and invoke this method binding in the custom selection listener before any custom logic.Although a table can handle selection automatically, there may be cases where you need to programmatically set the current row for an object on an iterator.
You can call the getKey() method on any view row to get a Key object that encapsulates the one or more key attributes that identify the row. You can also use a Key object to find a view row in a row set using the findByKey(). At runtime, when either the setCurrentRowWithKey or the setCurrentRowWithKeyValue built-in operation is invoked by name by the data binding layer, the findByKey() method is used to find the row based on the value passed in as a parameter before the found row is set as the current row.
The setCurrentRowWithKey and setCurrentRowWithKeyValue operations both expect a parameter named rowKey, but they differ precisely by what each expects that rowKey parameter value to be at runtime:
- setCurrentRowWithKey
-
setCurrentRowWithKeyexpects therowKeyparameter value to be the serialized string representation of a view row key. This is a hexadecimal-encoded string that looks like this:000200000002C20200000002C102000000010000010A5AB7DAD9
The serialized string representation of a key encodes all of the key attributes that might comprise a view row's key in a way that can be conveniently passed as a single value in a browser URL string or form parameter. At runtime, if you inadvertently pass a parameter value that is not a legal serialized string key, you may receive exceptions like
oracle.jbo.InvalidParamExceptionorjava.io.EOFExceptionas a result. In your web page, you can access the value of the serialized string key of a row by referencing therowKeyStrproperty of an ADF control binding (for example.#{bindings.SomeAttrName.rowKeyStr}) or the row variable of an ADF Faces table (e.g.#{row.rowKeyStr}). - setCurrentRowWithKeyValue
-
The
setCurrentRowWithKeyValueoperation expects therowKeyparameter value to be the literal value representing the key of the view row. For example, its value would be simply "201" to find product number201.
Note:
If you write custom code in an application module class and need to find a row based on a serialized string key passed from the client, you can use thegetRowFromKey() method in the JboUtil class in the oracle.jbo.client package:
static public Row getRowFromKey(RowSetIterator rsi, String sKey)
The first parameter is the view object instance in which you'd like to find the row. The second parameter is the serialized string format of the key.
23.3 Creating an Editable Table
You can create a table that allows the user to edit information within the table, and then commit those changes to the data source. To do this, you use operations that can modify data records associated with the collection (or the data control itself) to create command buttons, and place those buttons in a toolbar in the table. For example, you might use the Delete operation to create a button that allows a user to delete a record from the current range. Or you can use the built-in Submit button to submit changes.
Tip:
To create a table that allows you to insert a new record into the data store, see Section 23.4, "Creating an Input Table."It is important to note that these operations are executed only against objects in the ADF cache. You need to use the Commit operation on the root data control to actually commit any changes to the data source. You use the data control's Rollback operation to roll back any changes made to the cached object. If the page is part of a transaction within a bounded task flow, you would most likely use these operations to resolve the transaction in a task flow return activity. For more information, see Section 18.3, "Managing Transactions."
When you decide to use editable components to display your data, you have the option of the table displaying all rows as editable at once, or displaying all rows as read-only until the user double-clicks within the row. Figure 23-3 shows a table whose rows all have editable fields. The page renders using the components that were added to the page (for example, inputText, inputDate, and inputNumberSpinbox components).
Figure 23-4 shows the same table, but configured so that the user must double-click (or single-click if the row is already selected) a row in order to edit or enter data. Note that outputText components are used to display the data in the non-selected rows, even though the same input components as in Figure 23-3 were used to build the page. The only row that actually renders those components is the row selected for editing.
For more information about how ADF Faces table components handle editing, see the "Editing Data in Tables, Trees, and Tree Tables" section of the Oracle Fusion Middleware Web User Interface Developer's Guide for Oracle Application Development Framework.
23.3.1 How to Create an Editable Table
To create an editable table, you follow similar procedures to creating a basic table, then you add command buttons bound to operations. However, in order for the table to contain a toolbar, you need to add an ADF Faces component that associates the toolbar with the items in the collection used to build the table.
-
From the Data Controls panel, select a collection.
For example, to create a simple table in the StoreFront module that will allow you to edit products in the system, you would select the
Productscollection. -
Drag the collection onto a JSF page, and from the context menu, choose ADF Table.
This creates an editable table using input components.
-
Use the ensuing Edit Table Columns dialog to determine how the attributes should behave and appear as columns in your table. Be sure to select the Row Selection checkbox, which will allow the user to select the row to edit.
For more information about using this dialog to configure the table, see Section 23.2.1, "How to Create a Basic Table."
-
With the table selected in the Structure window, expand the Behavior section of the Property Inspector and set the EditingMode attribute. If you want all the rows to be editable select editAll. If you want the user to click into a row to make it editable, select clickToEdit.
-
From the Structure window, right-click the table component and select Surround With from the context menu.
-
In the Surround With dialog, ensure that ADF Faces is selected in the dropdown list, select the Panel Collection component, and click OK.
The
panelCollectioncomponent's toolbar facet will hold the toolbar which, in turn, will hold the command components used to update the data. -
In the Structure window, right-click the
panelCollection's toolbar facet folder and from the context menu, choose Insert inside toolbar > Toolbar.This creates a toolbar that already contains a default menu that allows users to change how the table is displayed and a Detach link that detaches the entire table and displays it such that it occupies the majority of the space in the browser window. For more information about the
panelCollectioncomponent, see the "Displaying Table Menus, Toolbars, and Status Bars" section of the Oracle Fusion Middleware Web User Interface Developer's Guide for Oracle Application Development Framework. -
From the Data Controls panel, select the operation associated with the collection of objects on which you wish the operation to execute, and drag it onto the
toolbarcomponent in the Structure window. This will place the databound command component inside the toolbar.For example, if you want to be able to delete a product record, you would drag the
Deleteoperation associated with theProductscollection. Figure 23-5 shows the operations associated with a collection. -
Choose Operations > ADF Toolbar Button from the context menu.
-
To create a Submit button that submits changes to the cache, right-click the toolbar component in the Structure window and choose Insert inside af:toolbar > Toolbar Button.
-
If the page is not part of a transaction within a bounded task flow, then you need to create buttons that allow the user to either commit or rollback the changes. From the Data Controls panel, drag the
CommitandRollbackoperations associated with the root-level data control, and drop them as either a command button or command link into the toolbar.Figure 23-6 shows the commit and roll back operations for the
StoreServiceAMDataControldata control.If the page is part of a transaction within a bounded task flow, then you can simply enter
CommitandRollbackas the values for the transaction resolution when creating the task flow return activity. For more information, see Section 18.3, "Managing Transactions."
23.3.2 What Happens When You Create an Editable Table
Creating an editable table is similar to creating a form used to edit records. Action bindings are created for the operations dropped from the Data Controls panel. For details on what happens when you create an editable table, see Section 22.4.2, "What Happens When You Create Command Buttons."
23.4 Creating an Input Table
You can create a table that allows users to insert a new blank row into a table and then add values for each column (any default values set on the corresponding entity or view object will be automatically populated).
23.4.1 How to Create an Input Table
When you create an input table, you want the user to see the new blank row in the context of the other rows within the current row set. To allow this insertion, you need to use the CreateInsert operation instead of the Create operation (as you would use with forms). The CreateInsert operation actually creates the new row within the row set instead of only in the cache.
ADF Faces components can be set so that one component refreshes based on an interaction with another component, without the whole page needing to be refreshed. This is known as partial page rendering. When the user clicks a button to create the new row, you want the table to refresh to display that new row. To have that happen, you need to configure the table to respond to that user action.
-
Create an editable table, as described in Section 23.3, "Creating an Editable Table."
-
If your table is not part of a bounded task flow, be sure to include buttons bound to the
CommitandRollbackoperations.
-
From the Data Controls panel, drag the CreateInsert operation associated with the dropped collection and drop it as a toolbar button into the toolbar. You may want to change the ID to something more recognizable, such as CreateInsert. This will make it easier to identify when you need to select it as the partial trigger.
-
In the Structure window, select the table component. In the Property Inspector, expand the Behavior section.
-
In the Property Inspector, click the dropdown menu for the PartialTriggers attribute, and select Edit.
-
In the Edit Property dialog, expand the toolbar facet for the
panelCollectioncomponent and then expand the toolbar that contains the CreateInsert command component. Select that component and shuttle it to the Selected panel. Click OK. This sets that component to be the trigger that will cause the table to refresh.
23.4.2 What Happens When You Create an Input Table
When you use the CreateInsert operation to create an input table, JDeveloper:
-
Creates an iterator binding for the collection, an action binding for the
CreateInsertoperation, and attribute bindings for the table. TheCreateInsertoperation is responsible for creating the new row in the row set. If you created command buttons or links using theCommitandRollbackoperations, JDeveloper also creates an action bindings for those operations. -
Inserts code in the JSF page for the table using ADF Faces
table,column, andinputTextcomponents, and in the case of the operations,commandButtoncomponents.
Example 23-5 shows the page definition file for an input table created from the Products collection (some attributes were deleted in the Edit Columns dialog when the collection was dropped).
Example 23-5 Page Definition Code for an Input Table
<executables>
<iterator Binds="Products" RangeSize="25"
DataControl="StoreServiceAMDataControl" id="ProductsIterator"/>
</executables>
<bindings>
<tree IterBinding="ProductsIterator" id="Products">
<nodeDefinition DefName="oracle.fodemo.storefront.store.queries.ProductsVO">
<AttrNames>
<Item Value="ProductId"/>
<Item Value="ProductName"/>
<Item Value="CostPrice"/>
<Item Value="ListPrice"/>
<Item Value="Description"/>
<Item Value="CategoryName"/>
<Item Value="CategoryDescription"/>
<Item Value="ProductImageId"/>
</AttrNames>
</nodeDefinition>
</tree>
<action IterBinding="ProductsIterator" id="CreateInsert"
RequiresUpdateModel="true" Action="createInsertRow"/>
<action id="Commit" RequiresUpdateModel="true" Action="commitTransaction"
DataControl="StoreServiceAMDataControl"/>
<action id="Rollback" RequiresUpdateModel="false"
Action="rollbackTransaction"
DataControl="StoreServiceAMDataControl"/>
</bindings>
Example 23-6 shows the code added to the JSF page that provides partial page rendering, using the CreateInsert command toolbar button as the trigger to refresh the table.
Example 23-6 Partial Page Trigger Set on a Command Button for a Table
<af:form>
<af:panelCollection id="pc1">
<f:facet name="menus"/>
<f:facet name="toolbar">
<af:toolbar id="tb1">
<af:commandToolbarButton actionListener="#{bindings.CreateInsert.execute}"
text="CreateInsert"
disabled="#{!bindings.CreateInsert.enabled}"
id="CreateInsert"/>
<af:commandToolbarButton actionListener="#{bindings.Commit.execute}"
text="Commit"
disabled="false" id="ctb2"/>
<af:commandToolbarButton actionListener="#{bindings.Rollback.execute}"
text="Rollback"
disabled="#{!bindings.Rollback.enabled}"
immediate="true" id="ctb3">
<af:resetActionListener/>
</af:commandToolbarButton>
</af:toolbar>
</f:facet>
<f:facet name="statusbar"/>
<af:table value="#{bindings.Products.collectionModel}" var="row"
rows="#{bindings.Products.rangeSize}"
emptyText="#{bindings.Products.viewable ? \'No data to display.\' :
\'Access Denied.\'}"
fetchSize="#{bindings.Products.rangeSize}"
rowSelection="single" partialTriggers="CreateInsert" id="t1">
<af:column sortProperty="ProductId" sortable="false"
headerText="#{bindings.Products.hints.ProductId.label}" id="c1">
<af:inputText value="#{row.ProductId}" simple="true"
required="#{bindings.Products.hints.ProductId.mandatory}"
columns="#{bindings.Products.hints.ProductId.displayWidth}"
maximumLength="#{bindings.Products.hints.
productId.precision}" id="it1"/>
</af:column>
.
.
.
</af:table>
</af:panelCollection>
</af:form>
23.4.3 What Happens at Runtime: How CreateInsert and Partial Page Refresh Work
When the button bound to the CreateInsert operation is invoked, the action executes, and a new instance for the collection is created and inserted as the page is rerendered. Because the button was configured to be a trigger that causes the table to refresh, the table redraws with the new empty row shown at the top. When the user clicks the button bound to the Commit action, the newly created rows in the row set are inserted into the database. For more information about partial page refresh, see the "Rendering Partial Page Content" chapter in the Oracle Fusion Middleware Web User Interface Developer's Guide for Oracle Application Development Framework.
23.4.4 What You May Need to Know About Creating a Row and Sorting Columns
If your table columns allow sorting, and the user has sorted on a column before inserting a new row, then that new row will not be sorted. To have the column sort with the new row, the user must first sort the column opposite to the desired sort, and then resort. This is because the table assumes the column is already sorted, so clicking on the desired sort order first will have no effect on the column.
For example, say a user had sorted a column in ascending order, and then added a new row. Initially, that row appears at the top. If the user first clicks to sort the column again in ascending order, the table will not resort, as it assumes the column is already in ascending order. The user must first sort on descending order and then ascending order.
If you want the data to automatically sort on a specific column in a specific order after inserting a row, then programmatically queue a SortEvent after the commit, and implement a handler to execute the sort. For more information about adding functionality to a declarative operation (such as the Commit operation), see Section 28.4, "Overriding Declarative Methods."
23.4.5 What You May Need to Know About Create and CreateInsert
When you use the Create or CreateInsert operation to declaratively create a new row, it performs the following lines of code:
// create a new row for the view object Row newRow = yourViewObject.createRow(); // mark the row as being "initialized", but not yet new newRow.setNewRowState(Row.STATUS_INITIALIZED);
However, if you are using the CreateInsert operation, it performs the additional line of code to insert the row into the row set:
// insert the new row into the view object's default rowset yourViewObject.insertRow(newRow);
When you create a row in an entity-based view object, the Transaction object associated with the current application module immediately takes note of the fact. The new entity row that gets created behind the view row is already part of the Transaction's list of pending changes. When a newly created row is marked as having the initialized state, it is removed from the Transaction's pending changes list and is considered a blank row in which the end user has not yet entered any data values. The term initialized is appropriate since the end user will see the new row initialized with any default values that the underlying entity object has defined. If the user never enters any data into any attribute of that initialized row, then it is as if the row never existed. At transaction commit time, since that row is not part of the Transaction's pending changes list, no INSERT statement will be attempted for it.
As soon as at least one attribute in an initialized row is set, it automatically transitions from the initialized status to the new status (Row.STATUS_NEW). At that time, the underlying entity row is enrolled in the Transaction's list of pending changes, and the new row will be permanently saved the next time you commit the transaction.
Note:
If the end user performs steps that result in creating many initialized rows but never populating them, it might seem like a recipe for a slow memory leak. However, the memory used by an initialized row that never transitions to the new state will eventually be reclaimed by the Java virtual machine's garbage collector.23.5 Providing Multiselect Capabilities
By default, when you drop a table component and set it to use row selection, it is set to allow a user to select a single row. You can change the table so that using the CTRL key or the SHIFT key, the user can select multiple rows, allowing the application to work on multiple rows at the same time.
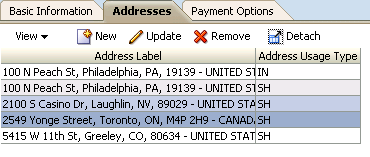
For example, Figure 23-7 shows the Addresses tab of the UpdateUserInfo page, which shows the current addresses for the logged-in user in a table. The user can select multiple addresses and then click the Remove toolbar button. This action removes the addresses from the data store.test
In order to allow the user to select and operate on more than one row, among other things, you need to change the rowSelection attribute to multiple. In Fusion web applications, operations (such as methods) work on the current data object, which the iterator keeps track of. When the rowSelection attribute is set to single (as it is by default when you select the Row Selection checkbox in the Edit Table Columns dialog when creating the table), the table is able to show the current data object as being selected, and it is also able to set any newly selected row to the current object on the iterator. If the same iterator is used on a subsequent page (for example, if the user selects a row and then clicks the command button to navigate to a page where the object can be edited), the selected object will be displayed. This selection and navigation works because the iterator and the component are working with a single object: the notion of the current row is the same because the different iterator bindings in different binding containers are bound to the same row set iterator.
However, when you set the rowSelection attribute to multiple, there potentially could be multiple selected objects. The ADF Model layer has no notion of "selected" as opposed to "current." You must add logic to the model layer that takes the component instance, reads the selected rows, and translates the selection state to the binding. The method can then perform some action on the selected rows.
23.5.1 How to Add Multiselect Capabilities
To add multiselect capabilities, you first modify certain table component attributes. Then you use a managed bean to handle setting the selected rows as the current rows.
Tip:
You can follow the same procedures for adding multiselect capabilities to a tree or tree table.Create a table as described in Section 23.2, "Creating a Basic Table," being sure to not select the Row Selection checkbox.
Note:
You should not select the Row Selection checkbox, because when you do, JDeveloper automatically binds theselectionListener attribute to the makeCurrent method on the CollectionModel class and the selectedRowKeys attribute to the selectedRow property on that class. Both are designed to work only for single selection tables. Make sure that for any table for which you need multiple selection, that neither of these attributes are populated.To add multiselect capabilities:
-
In the Structure window, select the table component and set the following attributes in the Property Inspector:
-
Row Selection:
multiple -
ID: an ID of your choice for the table
-
-
Create and register a managed bean for the page, if one does not already exist. You'll use the managed bean to handle the row selection and execute logic against the selection (for example, deleting the selected rows), so that it executes against all selected rows. For procedures for creating a managed bean, see Section 20.4, "Using a Managed Bean in a Fusion Web Application."
-
Add a property to the managed bean that represents the table component. Set the value of the property to the table ID value as set in Step 1, and the property class to be the ADF Faces table component class, as shown in Example 23-7.
-
Add getter and setter methods for the table to the managed bean, as shown in Example 23-8.
Example 23-8 Getter and Setter Methods for the Table Component
private RichTable _table1; public void setTable1(RichTable table1) { this.table1 = table1; } public RichTable getTable1() { return table1; }Tip:
You'll need to import the ADF Faces table class into the managed bean. JDeveloper can do this for you declaratively when you pressCTRL+ENTERafter adding the code in Example 23-8. -
Back in the JSP page, in the Structure window select the table component and set the binding attribute to be bound to the managed property you created in Step 3. For example:
binding="#{myBean.table1}"
This binding is what allows the application to work with the entire table component. For more information about the
bindingattribute and how it allows you access objects programmatically, refer to the Java EE 5 tutorial on Sun's web site (http://www.oracle.com/technetwork/java/index.html).Tip:
If you elected to use automatic component binding when creating the JSF page, then most of Steps 2 through 5 will have been done for you. You need only create the set method on the managed bean, as shown in Step 6. It is important, however, to understand the behavior of the page when using automatic component binding. For more information, see the "What You May Need to Know About Automatic Component Binding" section of the Oracle Fusion Middleware Web User Interface Developer's Guide for Oracle Application Development Framework. -
Add logic to allow the declarative operation or method to operate against the set of selected rows.
Example 23-9 shows the method named
deleteOnTable()that removes the selected rows from the address table on theupdateUserInfopage.Example 23-9 Deleting Multiple Rows on an Iterator
public void deleteOnTable(RichTable myTable) { RowKeySet rowKeySet = (RowKeySet) myTable.getSelectedRowKeys(); CollectionModel cm = (CollectionModel) myTable.getValue(); for (Object facesTreeRowKey : rowKeySet) { cm.setRowKey(facesTreeRowKey); JUCtrlHierNodeBinding rowData = (JUCtrlHierNodeBinding) cm.getRowData(); rowData.getRow().remove(); } }
23.5.2 What Happens at Runtime: How an Operation Executes Against Multiple Rows
When the user selects multiple rows and then clicks the command button, the application uses different contexts to access the expression factory to build an expression that resolves to the binding container. It then retrieves the iterator and the selected row keys on the component, and sets the selected rows on the binding. Next, it uses the collection model of the binding to remove the row and then reaccesses the component to display the collection with the now removed rows.
23.6 Modifying the Attributes Displayed in the Table
Once you use the Data Controls panel to create a table, you can then delete attributes, change the order in which they are displayed, change the component used to display them, and change the attribute binding for the component. You can also add new attributes, or rebind the table to a new data control.
23.6.1 How to Modify the Displayed Attributes
You can modify the following aspects of a table that was created using the Data Controls panel:
-
Change the binding for the label of a column
-
Change the attribute to which a UI component is bound
-
Change the UI component bound to an attribute
-
Reorder the columns in the table
-
Delete a column in the table
-
Add a column to the table
-
Enable selection and sorting
To change the attributes for a table:
-
In the Structure window, select the table component.
-
In the Property Inspector, expand the different sections to change the attributes for the table.
23.6.2 How to Change the Binding for a Table
Instead of modifying a binding, you can completely change the object to which the table is bound.
-
Right-click the table in the Structure window and choose Rebind to Another ADF Control.
-
In the Bind to ADF Control dialog, select the new collection to which you want to bind the table. Note that changing the binding for the table will also change the binding for all the columns. You can then use the procedures in Section 23.6.1, "How to Modify the Displayed Attributes" to modify those bindings.
Tip:
You can also rebind a table by dragging a different view object on top of the existing table.23.6.3 What Happens When You Modify Bindings or Displayed Attributes
When you simply modify how an attribute is displayed by moving the UI component or changing the UI component, JDeveloper changes the corresponding code on the JSF page. When you use the binding editors to add or change a binding, JDeveloper adds the code to the JSF page, and also adds the appropriate elements to the page definition file.