Chapter 3 Sun S3L Performance Guidelines

Introduction

This chapter provides a few guidelines for making best use of the performance benefits offered by Sun S3L. The range of topics covered include

• Sun S3L functions that benefit from cyclic distribution

• Sun S3L functions that benefit from distributing only the last axis

• Using shared memory

• Performance guidelines specific to FFT routines

• Performance guidelines specific to dense SVD routines

• Performance guidelines specific to dense linear system solvers

• Performance guidelines specific to banded solvers

• Performance guidelines specific to sparse linear systems solvers

• Performance guidelines specific to dense matrix operations

• Support for convolution, deconvolution, correlation, and autocorrelation

S3L Array Layout and Performance

Most Sun S3L functions perform best when their operand arrays are block-distributed along all axes. But there are exceptions to this generalization. This section discusses those exceptions.

Functions That Benefit From Cyclic Distributions

Functions that focus their operations on discrete subparts of an S3L array rather across the full array are likely to provide better load balancing and performance when their array operands are distributed cyclically rather than in simple block fashion. This is particularly true for the LU decomposition (S3L_lu_factor and S3L_lu_solve) and Singular Value Decomposition (S3L_gen_svd) functions.

This is illustrated by the examples shown in Figure 3-1 and Figure 3-2, which show a 16x16 array being distributed across a 1x4 process grid, first in simple block fashion and next in block cyclic fashion.

In Figure 3-1, a block size of 4 is used for the second axis. This means that the second array axis will be distributed in one pass across the process grid's second axis--in other words, it will be block-distributed.

Figure 3-1 Block Distribution of a 16x16 S3L Array on a 1x4 Process Grid

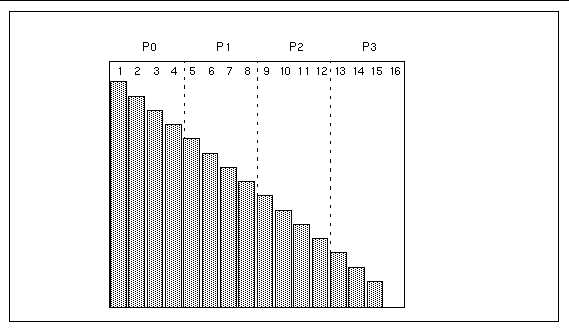
If the nature of the operation is such that every process will compute the sum of elements in the lower triangular part of the array (shaded portion) and send the results to the next processor, this distribution pattern will result in serious load imbalance among the processes. Since process 0 must perform many more iterations than the other processes, especially than process 3, overall computational time will be greater than it would be if better load balancing could be achieved.

In Figure 3-2, a block size of 2 is chosen for second axis. Although process 0 still has a larger section of the array operand than the other processes, cyclic distribution reduces the load differences significantly.

Figure 3-2 Block-Cyclic Distribution of a 16x16 S3L Array on a 1x4 Process Grid

Note that there is usually a limit to the load balancing gains that block-cyclic distribution can provide. In other words, setting block size to 1 is not likely to maximize performance, even for operations like the one just described. This limit results from a trade-off between the gains in load balancing that are provided by small block sizes and the gains in cache blocking efficiency that are achieved by loading array elements with consecutive indices into cache.

In addition to this trade-off, most of the nodal codes that underlay Sun S3L implement simple block distribution. Their optimal block size has to be matched to the optimal partitioning of the Sun S3L array.

In algorithms that are naturally load balanced--that is, where the amount of data each process has to process is approximately equal-- block-cyclic distribution has little effect on execution efficiency.

Distributing Only the Last Axis

The performance of some S3L functions can be enhanced by block-distributing only the last axis of the S3L array and making all other axes local. This rule applies to the FFT, sorting, and banded solver functions.

These functions are all optimized for operating on S3L arrays that are distributed in this manner. If an array that has a different type of distribution is being passed in as an argument, these functions automatically redistribute the array, perform the parallel computation and then restore it to its original form. Since this data redistribution introduces extra overhead, it is a good practice to ensure that S3L arrays passed to these functions follow this distribution plan.

Allocating Arrays in Shared Memory

Sun S3L supports the allocation of S3L arrays in shared memory. When an MPI program runs on a cluster of nodes, processes collocated on the same node can allocate their local array parts in that node's shared memory. Storing array sections in shared memory allows collocated processes to access each others array elements without going through MPI. This can yield significant performance improvements.

A special case of this would be an MPI application running on a single node. In this case, the entire S3L array could be allocated in shared memory.

Several Sun S3L functions are optimized for shared-memory accesses. That is, they employ different, more efficient algorithms when S3L arrays have been allocated in shared memory. These functions include the single and multidimensional parallel FFTs, as well as array transpose and sparse solver routines.

Use the S3L_declare or S3L_declare_detailed functions to allocate a parallel array in shared memory. For the type of allocation, specify either:

• S3L_USE_MMAP, which uses mmap() to allocate the S3L array

• S3L_USE_SHMGET, which uses shmget() (System V shared memory) to obtain Intimate Shared Memory. This is a form of shared memory in which data is always kept resident in physical memory and is never paged out.

  ---

  Note -

  Since physical memory is locked up by an application using Intimate Shared Memory, S3L_USE_SHMGET should only be used when the S3L array is small and the system is not being shared with other users.

  ---

Numbers of Processes

Many Sun S3L routines employ a serial algorithm when called from an application running on a single process and a different, parallel algorithm when called from a multiprocess application. When those Sun S3L routines are executed on a small number of processes--two or three--they are likely to be slower than the serial version running on a single process. This is because the higher overhead involved in the parallel process can overshadow any gains resulting from parallelization of the operation.

This means that, in general, MPI applications that call Sun S3L routines should be executing on at least four processes.

Function-Specific Guidelines

This section discusses performance-tuning for specific S3L functions. It does not cover all Sun S3L functions.

S3L FFT (Fast Fourier Transform)

Complex to Complex FFTs

Sun S3L provides two functions for computing the forward and backward Fourier transforms of one-, two-, and three-dimensional complex arrays: S3L_fft and S3L_ifft.

In Sun S3L, the term forward FFT is used for operations with a negative sign in the exponential factors.

Before calling either of these functions, however, an FFT setup must be computed, using S3L_fft_setup. This setup will contain the FFT twiddle factors and other internal data specific to the algorithm that will be used in the FFT computation.

The setup data depend only on the size, type and layout of the S3L array. Consequently, once they are computed they can be applied in the FFT computation of any other S3L arrays that have the same size, type and layout.

The S3L array must already have been allocated before calling S3L_fft_setup. The setup routine specifies the S3L array of interest by using its array handle, which was returned by a previous call to S3L_declare or S3L_declare_detailed.

The following code example shows S3L_fft_setup being used to create a setup for the S3L array a.

Example 3-1

c
    integer*4 setup_id, ier
    integer*8
c
c compute an FFT setup for a parallel
c S3L array identified by a.
c
c Note that a must have been properly allocated via
c a call to S3L_declare or 3L_declare_detailed.
c
    cakk s3l_fft_setup(a,setup_id,ier)

S3L_fft_setup returns a value of type integer*4 (F77/F90) or int (C/C++) in setup_id. Subsequent calls to S3L_fft and S3L_ifft use the setup_id value to reference the FFT setup of interest.

Use S3L_fft to compute a forward FFT.

call s3l_fft(a,setup_id,ier)

Use S3L_ifft to compute the inverse FFT.

call s3l_ifft(a,setup_id,ier)

Note that the same setup can be used for both the forward and the inverse FFT. S3L_fft does not scale the results, so a forward FFT followed by an inverse FFT results in the original data being scaled by the product of the array extents.

Note also that, for one-dimensional FFTs, there are certain requirements regarding the size of the FFT and the number of processes used to compute it. For details, see "S3L_fft " and "S3L_ifft " or the S3L_fft and S3L_ifft man pages.

S3L_fft and S3L_ifft can be used to compute the Discrete Fourier Transform of arrays of up to three dimensions.

When arrays with more than three dimensions are to be transformed or, when more control over how the FFTs are applied to the array dimensions is desired, use S3L_fft_detailed. This function uses the same setup_id as S3L_fft and S3L_ifft, but accepts additional parameters. S3L_fft_detailed allows the programmer to specify

• the axis along which the transform is to be applied

• the direction of the FFT (1 for forward, -1 for inverse)

Once the FFT computations have completed, the resources associated with that FFT setup should be freed by calling S3L_fft_free_setup, as in the following F77 example.

call s3l_fft_free_setup(setup_id,ier)

Sun S3L FFT Optimizations

The Sun S3L FFT is optimized for use by message-passing applications. It works for S3L arrays with arbitrary distributions a multiprocess process grid. For certain data distributions, maximum efficiency can be obtained.

For example, the algorithm used for a two-dimensional complex-to-complex parallel FFT is optimized for arrays distributed along their second dimension, where the number of processes is a power of two. For maximum efficiency, both axes of the array must be divisible by the number of processes.

When the array distribution allows fast algorithms to be used, the two-dimensional FFT consists essentially of multiple one-dimensional FFTs performed along the array columns local to the process. It then transposes the array in such a way that each process has a number of local rows. This is followed by a second set of local one-dimensional FFTs. Finally, the data are transposed back to the original distribution.

This sequence is illustrated by the diagrams in Figure 3-3 through Figure 3-5.

Figure 3-3 Phase 1 of Two-Dimensional FFT Performing Independent One-Dimensional FFT

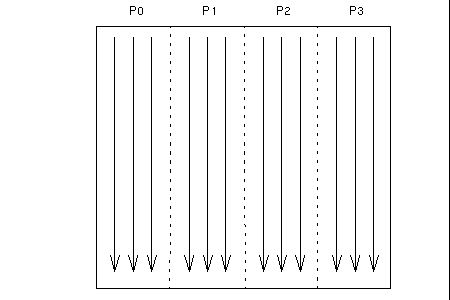
Figure 3-4 Phase 2 of Two-Dimensional FFT Performing Local Transpositions

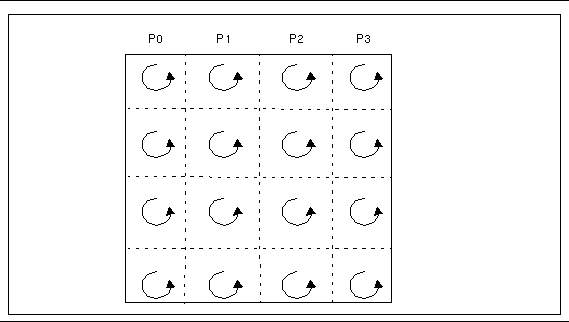
Figure 3-5 Phase 3 of Two-Dimensional FFT Performing Global Transpositions

When the data are distributed in suboptimal ways-- for example, along both dimensions on a rectangular process-grid--a global communication step is usually performed first to redistribute the data to its optimal distribution and then the optimized FFT is performed. This redistribution step increases execution overhead.

Dense Singular Value Decomposition (SVD)

Sun S3L includes routines for performing the singular value decomposition of real single- or double-precision arrays. These routines include options for computing only the singular values or the right and/or left singular eigenvectors.

For the S3L_gen_svd function, optimal performance is achieved when block-cyclic distribution is used on the S3L array operand. S3L_gen_svd works best on large arrays. Performance is also better when S3L_gen_svd executes on a small number of processes.

Sorting and Ranking S3L Arrays

Sun S3L includes sorting routines for parallel sorting of one-dimensional arrays or multidimensional arrays along a user-specified axis. It also includes routines for computing the grade (rank) of the elements of an array.

The sorting and grading routines are most efficient when the arrays are block distributed. For multidimensional sorts and grades, performance is best when the axis to be sorted or graded is local to a process.

The sort routines use a variation of the sample sort algorithm. In a coordinated operation, all processors extract a random sample of the data. The distribution of this sample should match as closely as possible the distribution of the data to be sorted. Based on this sample, all processes split their data into np packets, each destined for a particular process. A global interprocess communication stage then collects the packets into the appropriate processes. Each process then independently sorts its own data using a quicksort algorithm. Finally, all the processes coordinate to restore the data to its original distribution.

The first communication stage, where packets of data are sent to the appropriate processes, is more intensive than the operation that restores the original distribution. This is because the second communication stage only involves exchanges between processes with neighboring ranks.

In general, the parallel S3L sort routines exhibit good scaling characteristics. While some data distribution patterns can affect the quality of load balancing and the performance of local sorts, the internal parameters of the parallel algorithm have been chosen to achieve good performance for most cases of data distribution.

Sorting single-precision floating-point numbers is faster than sorting double-precision floating-point numbers. Also, sorting 64-byte integers can be slower than sorting 64-byte floating-point numbers.

Dense Linear Systems Solvers

Sun S3L includes dense linear systems solvers that provide solutions to linear systems of equations for real and complex general matrices.

LU operations are carried out in two stages. First, one or more matrices A are decomposed into their LU factors using Gaussian elimination with partial pivoting. This is done using S3L_lu_factor. Then, the generated LU factors are used by S3L_lu_solve to solve the linear system AX=B or by S3L_lu_invert to compute the inverse of A.

The LU decomposition routine, which is derived from the ScaLAPACK implementation, uses a parallel block-partitioned algorithm. The Sun S3L routine exploits the optimized nodal libraries, consisting primarily of a specialized matrix-matrix multiply routine, to speed up the computation. In addition, an optimized communication scheme is used to reduce the total number of interprocess communication steps.

The LU decomposition algorithm used in Sun S3L is aware of the size of the external cache memory and other CPU parameters and selects the most efficient methods based on that information.

The S3L LU decomposition routine is particularly efficient when factoring 64-bit (double-precision) floating-point matrices that have been allocated using the S3L_USE_MEMALIGN64 option so that their local subgrids are in 64-byte aligned memory addresses. Performance is best in such cases when a block size of 24 or 48 is used.

As mentioned in Chapter 2, Sun S3L Arrays, block-cyclic distribution should be used for LU factorization and solution routines.

Also, process grids having the form 1 x np, where np is the total number of processes, provide best performance when the number of processes and the size of the arrays is relatively small. However, when the size of the array to be factored is very large, it is better to specify rectangular process grids of the form nq x np, rather than square process grids.

Banded Solvers

S3L includes both a tridiagonal and a general banded linear solver.

The tridiagonal solver does not perform pivoting, so it should be used only for systems that are known to be stable, such as diagonally dominant tridiagonal systems.

The banded solver performs partial pivoting, so it exhibits better stability than the tridiagonal solvers.

Both solvers will perform optimally when the LHS arrays are block-distributed along their last axis, the RHS arrays are block-distributed along their first axis, and the same block size is used for both distributions.

The S3L_gen_trid_factor function is used to factor a tridiagonal system of equations, where the main diagonal, upper subdiagonal and lower subdiagonal are given in three S3L arrays, D, U, and L.

S3L_gen_trid_solve, is used to solve a tridiagonal system of equations whose RHS matrix is given in an S3L array B, using the factorization results from a previous call to S3L_gen_trid_factor.

The banded solvers have linear complexity and their interprocess communication requirements are not great. Consequently, these banded solvers can deliver performance on clusters of small nodes that is similar to what would be achieved on a single node with many CPUs.

Sparse Linear Systems Solvers

Given a general square sparse matrix A and an RHS vector b, S3L_gen_iter_solve solves the linear system of equations Ax = b using an iterative algorithm, with or without preconditioning.

S3L_gen_iter_solve implements several different algorithms, which the programmer can select. These include

• BiConjugate Gradient Stabilized (BiCGSTAB)

• Conjugate Gradient (CG)

• Conjugate Gradient Squared (CGS)

• Conjugate Residuals (CR)

• Restarted Generalized Minimum Residual (GMRES)

• Quasi-Minimal Residual (QMR)

• Richardson method

If preconditioning is used, the programmer can choose point Jacobi or incomplete LU as the method. S3L_gen_iter_solve also allows the programmer to specify a number of other algorithm-specific parameters, including

• the convergence/divergence criteria

• the initial guess

• the maximum number of iterations

Sparse matrix utilities

Sun S3L includes a set of utilities for declaring and initializing sparse matrices. Other utilities for operating on sparse matrices are provided as well.

S3L_declare_sparse declares an S3L sparse array and allocates all required memory to store its elements and sparsity pattern representation.

S3L_rand_sparse creates a random sparse matrix with a random sparsity pattern in either the Coordinate (COO) format or the Compressed Sparse Row (CSR) format. Upon successful completion, it returns an S3L array handle representing this random sparse matrix.

S3L_read_sparse reads a sparse array from a data file. Similarly, S3L_write_sparse writes a sparse S3L array to a file. S3L_print_sparse prints a sparse array to standard output.

S3L_matvec_sparse multiplies a sparse array with a dense vector.

Dense Matrix Operations

Sun S3L includes optimized parallel functions for performing the following dense matrix operations:

• matrix-matrix and matrix-vector multiplication

• inner product computation

• outer product computation

• 2-norm computation

These functions have been optimized for various multiprocess configurations and array sizes.They implement different algorithms according to the particular configuration. Among the algorithms that these functions may employ are the Broadcast-Multiply-Roll, Cannon, and Broadcast-Broadcast Multiply.

The source data to be used by the dense matrix operations should be aligned so that no extra redistribution costs are imposed. For example, if rectangular matrix A, which is distributed along the last axis of a 1 x np process grid, will be multiplied with an n x 1 vector x, the vector multiplier should be distributed onto np processes with the same block size as is used for the distribution of A along the second axis.

In general the performance of dense matrix operations is similar for both pure block and block-cyclic distributions.

If both operand arrays in a dense matrix function do not have the same type of distribution--that is, one is pure block-distributed and the other block-cyclic--the dense matrix multiplication routine will automatically redistribute as necessary to properly align the arrays. However, this redistribution can add considerable overhead to the operation, so it is best if the application ensures that they have like distributions beforehand.

In general, the dense matrix parallel algorithm is more efficient when the matrices being multiplied are large. This is because the large matrices take advantage of the dominance of the O(N3) computational complexity over the O(N2) communication requirements.

The benefit of larger matrices can be offset, however, when the matrices are so large that they occupy nearly all of total system memory. Because additional internal data structures are allocated for the parallel algorithm, swapping out of memory may be required, which can degrade performance.

When the multiple instance capability of the dense matrix functions is used, performance can be significantly aided by making the instances local.

Convolution, Deconvolution, Correlation, Autocorrelation

Sun S3L includes functions for performing various signal processing computations, such as convolving or deconvolving two one- or two-dimensional arrays and for computing the correlation or autocorrelation of a signal. These functions are based on the Sun S3L FFT functions. These functions have been optimized to eliminate unnecessary computations.

For example, the convolution of the two-dimensional arrays (images) A and B can be achieved by

• Computing the two-dimensional FFT of A

• Computing the two-dimensional FFT of B

• Finding the pointwise product of the result

• Computing the inverse two-dimensional FFT of the previous result