ONC+ Developer's Guide

XDR Data Type Declarations

Each of the sections that follow:

Describes a data type defined in the XDR standard
Shows how that data type is declared in the language
Includes a graphic illustration of the encoding

For each data type in the language a general paradigm declaration is shown. Note that angle brackets (< and >) denote variable-length sequences of data and square brackets ([and]) denote fixed-length sequences of data. n, m, and r denote integers. For the full language specification, refer to XDR Language Specification.

Some data types include specific examples. A more extensive example is given in the section XDR Data Description.

Signed Integer

An XDR signed integer is a 32-bit datum that encodes an integer in the range [-2147483648,2147483647]. The integer is represented in two's complement notation; the most and least significant bytes are 0 and 3, respectively.

Declaration

Integers are declared:

int identifier;

Signed Integer Encoding

Unsigned Integer

An XDR unsigned integer is a 32-bit datum that encodes a nonnegative integer in the range [0, 4294967295]. The integer is represented by an unsigned binary number that has most- and least-significant bytes of 0 and 3 respectively.

Declaration

An unsigned integer is declared as follows.

unsigned int identifier;

Unsigned Integer Encoding

Enumerations

Enumerations have the same representation as signed integers and are handy for describing subsets of the integers. The encoding for enumerations is the same as shown in Signed Integer Encoding.

Enumerated data is declared as follows.

enum {name-identifier = constant, ... } identifier;

For example, an enumerated type could represent the three colors red, yellow, and blue as follows.

enum {RED = 2, YELLOW = 3, BLUE = 5} colors;

Do not assign to an enum an integer that has not been assigned in the enum declaration.

Booleans

Booleans are important enough and occur frequently enough to warrant their own explicit type in the standard. Booleans are integers of value 0 or 1. The encoding for Booleans is the same as show in Signed Integer Encoding.

Booleans are declared as follows.

bool identifier;

This is equivalent to:

enum {FALSE = 0, TRUE = 1} identifier;

Hyper Integer and Unsigned Hyper Integer

The standard defines 64–bit (8-byte) numbers called hyper int and unsigned hyper int with representations that are the obvious extensions of integer and unsigned integer, defined previously. They are represented in two's complement notation; the most-significant and least-significant bytes are 0 and 7, respectively.

Declaration

Hyper integers are declared as follows.

hyper int  identifier;
unsigned hyper int identifier;

Hyper Integer Encoding

Floating Point

The standard defines the floating-point data type float (32 bits or 4 bytes). The encoding used is the IEEE standard for normalized single-precision floating-point numbers [1]. The following three fields describe the single-precision floating-point number:

S: The sign of the number. Values 0 and 1 represent positive and negative respectively. One bit.

E: The exponent of the number, base 2. Eight bits are in this field. The exponent is biased by 127.

F: The fractional part of the number's mantissa, base 2. Twenty-three bits are in this field.

Therefore, the floating-point number is described by.

(-1)**S * 2**(E-Bias) * 1.F

Declaration

Single-precision floating-point data is declared as follows.

float identifier;

Double-precision floating-point data is declared as follows.

double identifier;

Double-Precision Floating Point Encoding

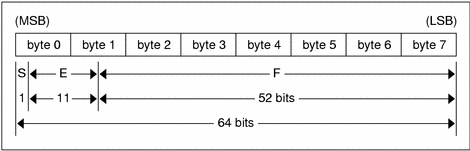
Just as the most and least significant bytes of an integer are 0 and 3, the most-significant and least-significant bits of a double-precision floating-point number are 0 and 63. The beginning bit, and most significant bit, offsets of S, E, and F are 0, 1, and 12 respectively.

These offsets refer to the logical positions of the bits, not to their physical locations, which vary from medium to medium.

Consult the IEEE specifications about the encoding for signed zero, signed infinity (overflow), and de-normalized numbers (underflow) [1]. According to IEEE specifications, the NaN (not a number) is system dependent and should not be used externally.

Quadruple-Precision Floating Point

The standard defines the encoding for the quadruple-precision floating-point data type quadruple (128 bits or 16 bytes). The encoding used is the IEEE standard for normalized quadruple-precision floating-point numbers [1]. The standard encodes the following three fields, which describe the quadruple-precision floating-point number.

S: The sign of the number. Values 0 and 1 represent positive and negative respectively. One bit.

E: The exponent of the number, base 2. Fifteen bits are in this field. The exponent is biased by 16383.

F: The fractional part of the number's mantissa, base 2. One hundred eleven bits are in this field.

Therefore, the floating-point number is described by:

(-1)**S * 2**(E-Bias) * 1.F

Declaration

quadruple identifier;

Quadruple-Precision Floating Point Encoding

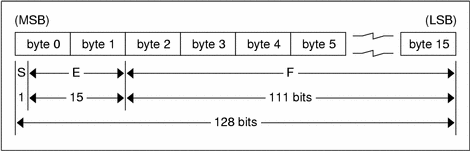
Just as the most-significant and least-significant bytes of an integer are 0 and 3, the most-significant and least-significant bits of a quadruple-precision floating- point number are 0 and 127. The beginning bit, and most-significant bit, offsets of S, E, and F are 0, 1, and 16 respectively. These offsets refer to the logical positions of the bits, not to their physical locations, which vary from medium to medium.

Fixed-Length Opaque Data

At times, fixed-length uninterpreted data needs to be passed among machines. This data is called opaque.

Declaration

Opaque data is declared as follows.

opaque identifier[n];

In this declaration, the constant n is the static number of bytes necessary to contain the opaque data. The n bytes are followed by enough (0 to 3) residual zero bytes r to make the total byte count of the opaque object a multiple of four.

Fixed-Length Opaque Encoding

The n bytes are followed by enough (0 to 3) residual zero bytes r to make the total byte count of the opaque object a multiple of four.

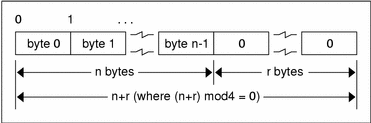
Variable-Length Opaque Data

The standard also provides for variable-length counted opaque data. Such data is defined as a sequence of n (numbered 0 through n-1) arbitrary bytes to be the number n encoded as an unsigned integer, as described subsequently, and followed by the n bytes of the sequence.

Byte b of the sequence always precedes byte b+1 of the sequence, and byte 0 of the sequence always follows the sequence's length. The n bytes are followed by enough (0 to 3) residual zero bytes, r, to make the total byte count a multiple of four.

Declaration

Variable-length opaque data is declared in the following way.

opaque identifier<m>;

opaque identifier<>;;

The constant m denotes an upper bound of the number of bytes that the sequence can contain. If m is not specified, as in the second declaration, it is assumed to be (2**32) - 1, the maximum length. For example, a filing protocol might state that the maximum data transfer size is 8192 bytes, as follows.

opaque filedata<8192>;

Variable-Length Opaque Encoding

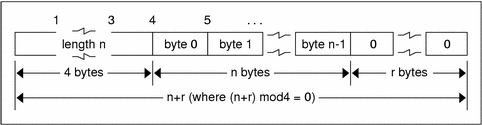
Do not encode a length greater than the maximum described in the specification.

Counted Byte Strings

The standard defines a string of n (numbered 0 through n-1) ASCII bytes to be the number n encoded as an unsigned integer, as described previously, and followed by the n bytes of the string. Byte b of the string always precedes byte b+1 of the string, and byte 0 of the string always follows the string's length. The n bytes are followed by enough (0 to 3) residual zero bytes r to make the total byte count a multiple of four.

Declaration

Counted byte strings are declared as follows.

string object<m>;

string object<>;

The constant m denotes an upper bound of the number of bytes that a string can contain. If m is not specified, as in the second declaration, it is assumed to be (2**32) - 1, the maximum length. The constant m would normally be found in a protocol specification. For example, a filing protocol might state that a file name can be no longer than 255 bytes, as follows.

string filename<255>;

String Encoding

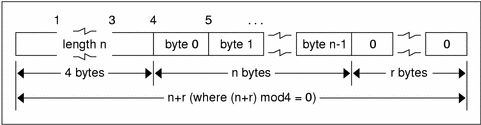
Do not encode a length greater than the maximum described in the specification.

Fixed-Length Array

Fixed-length arrays of elements numbered 0 through n-1 are encoded by individually encoding the elements of the array in their natural order, 0 through n-1. Each element's size is a multiple of 4 bytes. Though all elements are of the same type, the elements might have different sizes. For example, in a fixed-length array of strings, all elements are of type string, yet each element varies in its length.

Declaration

Declarations for fixed-length arrays of homogenous elements are in the following form.

type-name identifier[n];

Fixed-Length Array Encoding

Variable-Length Array

Counted arrays enable variable-length arrays to be encoded as homogeneous elements. The element count n, an unsigned integer, is followed by each array element, starting with element 0 and progressing through element n-1.

Declaration

The declaration for variable-length arrays follows this form.

type-name identifier<m>;

type-name identifier<>;

The constant m specifies the maximum acceptable element count of an array. If m is not specified, it is assumed to be (2**32) - 1.

Counted Array Encoding

Do not encode a length greater than the maximum described in the specification.

Structure

The components of the structure are encoded in the order of their declaration in the structure. Each component's size is a multiple of 4 bytes, though the components might be different sizes.

Declaration

Structures are declared as follows.

struct {
  	component-declaration-A;
  	component-declaration-B;
  	...
 } identifier;

Structure Encoding

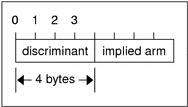
Discriminated Union

A discriminated union is a type composed of a discriminant followed by a type selected from a set of prearranged types according to the value of the discriminant. The type of discriminant is either int, unsigned int, or an enumerated type, such as bool. The component types are called “arms” of the union, and are preceded by the value of the discriminant that implies their encoding.

Declaration

Discriminated unions are declared as follows.

union switch (discriminant-declaration) {
  	case discriminant-value-A:
  		arm-declaration-A;
  	case discriminant-value-B:
  		arm-declaration-B;
  	...
  	default:
  		default-declaration;
 } identifier;

Each case keyword is followed by a legal value of the discriminant. The default arm is optional. If the arm is not specified, then a valid encoding of the union cannot take on unspecified discriminant values. The size of the implied arm is always a multiple of 4 bytes.

The discriminated union is encoded as its discriminant followed by the encoding of the implied arm.

Discriminated Union Encoding

Void

An XDR void is a 0-byte quantity. Voids are useful for describing operations that take no data as input or no data as output. They are also useful in unions, in which some arms might contain data and others do not.

Declaration

The declaration is simply as follows.

void;

Constant

const is used to define a symbolic name for a constant. It does not declare any data. The symbolic constant can be used anywhere a regular constant can be used.

The following example defines a symbolic constant DOZEN, equal to 12.

const DOZEN = 12;

Declaration

The declaration of a constant follows this form.

const name-identifier = n;

Typedef

Typedef does not declare any data either, but serves to define new identifiers for declaring data. The syntax is:

typedef declaration;

The new type name is actually the variable name in the declaration part of the typedef. The following example defines a new type called eggbox using an existing type called egg and the symbolic constant DOZEN.

typedef egg eggbox[DOZEN];

Variables declared using the new type name have the same type as the new type name would have in the typedef, if it were considered a variable. For example, the following two declarations are equivalent in declaring the variable fresheggs:

eggbox fresheggs;
 egg fresheggs[DOZEN];

When a typedef involves a struct, enum, or union definition, you can use another (preferred) syntax to define the same type. In general, a typedef of the following form:

typedef <<struct, union, or enum definition>> identifier;

can be converted to the alternative form by removing the typedef part and placing the identifier after the struct, enum, or union keyword instead of at the end. For example, here are the two ways to define the type bool.

typedef enum {/* using typedef */
   FALSE = 0,
   TRUE = 1
} bool;
enum bool {/* preferred alternative */
   FALSE = 0,
   TRUE = 1
};

This syntax is preferred because you do not have to go to the end of a declaration to learn the name of the new type.

Optional-Data

The optional-data union occurs so frequently that it is given a special syntax of its own for declaring it. It is declared as follows.

type-name *identifier;

This syntax is equivalent to the following union:

union switch (bool opted) {
 	case TRUE:
 	type-name element;
 	case FALSE:
 	void;
} identifier;

The optional-data syntax is also equivalent to the following variable-length array declaration, because the Boolean opted can be interpreted as the length of the array.

type-name identifier<1>;

Optional data is useful for describing recursive data-structures, such as linked lists and trees.