Developing Applications That Use GSS-API
This section shows how to implement secure data exchange using GSS-API. The section focuses on those functions that are most central to using GSS-API. For more information, see Appendix B, GSS-API Reference, which contains a list of all GSS-API functions, status codes, and data types. To find out more about any GSS-API function, check the individual man page.
The examples in this manual follow a simple model. A client application sends data directly to a remote server. No mediation by transport protocol layers such as RPC occurs.
Generalized GSS-API Usage
-
Each application, both sender and recipient, acquires credentials explicitly, unless credentials have been acquired automatically.
-
The sender initiates a security context. The recipient accepts the context.
-
The sender applies security protection to the data to be transmitted. The sender either encrypts the message or stamps the data with an identification tag. The sender then transmits the protected message.
Note –The sender can choose not to apply either security protection, in which case the message has only the default GSS-API security service, that is, authentication.
-
The recipient decrypts the message if needed and verifies the message if appropriate.
-
(Optional) The recipient returns an identification tag to the sender for confirmation.
-
Both applications destroy the shared security context. If necessary, the allocations can also deallocate any remaining GSS-API data.
The general steps for using GSS-API are as follows:
The calling application is responsible for freeing all data space that has been allocated.
Applications that use GSS-API need to include the file gssapi.h.
Working With Credentials in GSS-API
A credential is a data structure that provides proof of an application's claim to a principal name. An application uses a credential to establish that application's global identity. Additionally, a credential may be used to confirm an entity's privileges.
GSS-API does not provide credentials. Credentials are created by the security mechanisms that underly GSS-API, before GSS-API functions are called. In many cases, a user receives credentials at login.
A given GSS-API credential is valid for a single principal. A single credential can contain multiple elements for that principal, each created by a different mechanism. A credential that is acquired on a machine with multiple security mechanisms is valid if that credential is transferred to a machine with a subset of those mechanisms. GSS-API accesses credentials through the gss_cred_id_t structure. This structure is called a credential handle. Credentials are opaque to applications. Thus, the application does not need to know the specifics of a given credential.
Credentials come in three forms:
-
GSS_C_INITIATE– Identifies applications that only initiate security contexts -
GSS_C_ACCEPT– Identifies applications that only accept security contexts -
GSS_C_BOTH– Identifies applications that can initiate or accept security contexts
Acquiring Credentials in GSS-API
Before a security context can be established, both the server and the client must acquire their respective credentials. A credential can be reused until that credential expires, after which the application must reacquire the credential. Credentials that are used by the client and credentials that are used by the server can have different lifetimes.
GSS-API-based applications can acquire credentials in two ways:
-
By specifying the value
GSS_C_NO_CREDENTIAL, which indicates a default credential, when the context is established
In most cases, gss_acquire_cred() is called only by a context acceptor, that is, a server. A context initiator, that is, a client, typically receives credentials at login. A client, therefore, can usually specify the default credential. The server can also bypass gss_acquire_cred() and use that server's default credential instead.
A client's credential proves that client's identity to other processes. A server acquires a credential to enable that server to accept a security context. So when a client makes an ftp request to a server, that client might already have a credential from login. GSS-API automatically retrieves the credential when the client attempts to initiate a context. The server program, however, explicitly acquires credentials for the requested service (ftp).
If gss_acquire_cred() completes successfully, then GSS_S_COMPLETE is returned. If a valid credential cannot be returned, then GSS_S_NO_CRED is returned. See the gss_acquire_cred(3GSS) man page for other error codes. For an example, see “Acquiring Credentials” in Chapter 8.
gss_add_cred() is similar to gss_acquire_cred(). However, gss_add_cred() enables an application
to use an existing credential to create a new handle or to add a new credential
element. If GSS_C_NO_CREDENTIAL is specified as the existing
credential, then gss_add_cred() creates a new credential
according to the default behavior. See the gss_add_cred(3GSS) man
page for more information.
Working With Contexts in GSS-API
The two most significant tasks for GSS-API in providing security are to create security contexts and to protect data. After an application acquires the necessary credentials, a security context must be established. To establish a context, one application, typically a client, initiates the context, and another application, usually a server, accepts the context. Multiple contexts between peers are allowed.
The communicating applications establish a joint security context by exchanging authentication tokens. The security context is a pair of GSS-API data structures that contain information to be shared between the two applications. This information describes the state of each application in terms of security. A security context is required for protection of data.
Initiating a Context in GSS-API
The gss_init_sec_context() function is used to start a security context between an application and a remote peer. If successful, this function returns a context handle for the context to be established and a context-level token to send to the acceptor.
-
Acquire credentials, if necessary, with gss_acquire_cred(). Typically, the client receives credentials at login. gss_acquire_cred() can only retrieve initial credentials from the running operating system.
-
Import the name of the server into GSS-API internal format with gss_import_name(). See Names in GSS-API for more information about names and gss_import_name().
Before calling gss_init_sec_context(), the client should perform the following tasks:
When calling gss_init_sec_context(), a client typically passes the following argument values:
-
GSS_C_NO_CREDENTIALfor the cred_handle argument, to indicate the default credential. -
GSS_C_NULL_OIDfor the mech_type argument, to indicate the default mechanism. -
GSS_C_NO_CONTEXTfor the context_handle argument, to indicate an initial null context. Because gss_init_sec_context() is usually called in a loop, subsequent calls should pass the context handle that was returned by previous calls. -
GSS_C_NO_BUFFERfor the input_token argument, to indicate an initially empty token. Alternatively, the application can pass a pointer to a gss_buffer_desc object whose length field has been set to zero. -
The name of the server, imported into internal GSS-API format with gss_import_name().
Applications are not bound to use these default values. Additionally, a client can specify requirements for other security parameters with the req_flags argument. The full set of gss_init_sec_context() arguments is described below.
The context acceptor might require several handshakes to establish a context. That is, an acceptor can require the initiator to send more than one piece of context information before the context is fully established. Therefore, for portability, context initiation should always be done as part of a loop that checks whether the context has been fully established.
If the context is not complete, gss_init_sec_context() returns a major status code of GSS_C_CONTINUE_NEEDED. Therefore, a loop should use the return value from gss_init_sec_context() to test whether to continue the initiation loop.
The client passes context information to the server in the form of the output token, which is returned by gss_init_sec_context(). The client receives information back from the server as an input token. The input token can then be passed as an argument in subsequent calls of gss_init_sec_context(). If the received input token has a length of zero, however, then no more output tokens are required by the server.
Therefore, besides checking for the return status of gss_init_sec_context(), the loop should check the input token's length. If the length
has a nonzero value, another token needs to be sent to the server. Before
the loop begins, the input token's length should be initialized to zero. Either
set the input token to GSS_C_NO_BUFFER or set the structure's
length field to a value of zero.
The following pseudocode demonstrates an example of context establishment from the client side.
context = GSS_C_NO_CONTEXT
input token = GSS_C_NO_BUFFER
do
call gss_init_sec_context(credential, context, name, input token,
output token, other args...)
if (there's an output token to send to the acceptor)
send the output token to the acceptor
release the output token
if (the context is not complete)
receive an input token from the acceptor
if (there's a GSS-API error)
delete the context
until the context is completeA real loop would be more complete with more extensive error-checking. See Establishing a Security Context With the Server for a real example of such a context-initiation loop. Additionally, the gss_init_sec_context(3GSS) man page provides a less generic example.
In general, the parameter values returned when a context is not fully established are those values that would be returned when the context is complete. See the gss_init_sec_context() man page for more information.
If gss_init_sec_context() completes successfully, GSS_S_COMPLETE is returned. If a context-establishment token is required from the peer application, GSS_S_CONTINUE_NEEDED is returned. If errors occur, error codes are returned as shown in the gss_init_sec_context(3GSS) man page.
If context initiation fails, the client should disconnect from the server.
Accepting a Context in GSS-API
The other half of context establishment is context acceptance, which is done through the gss_accept_sec_context() function. In a typical scenario, a server accepts a context that has been initiated by a client with gss_init_sec_context().
The main input to gss_accept_sec_context() is an input token from the initiator. The initiator returns a context handle as well as an output token to be returned to the initiator. Before gss_accept_sec_context() can be called, however, the server should acquire credentials for the service that was requested by the client. The server acquires these credentials with the gss_acquire_cred() function. Alternatively, the server can bypass explicit acquisition of credentials by specifying the default credential, that is, GSS_C_NO_CREDENTIAL, when the server calls gss_accept_sec_context().
When calling gss_accept_sec_context(), the server can set the following arguments as shown:
-
cred_handle – The credential handle returned by gss_acquire_cred(). Alternatively,
GSS_C_NO_CREDENTIALcan be used to indicate the default credential. -
context_handle –
GSS_C_NO_CONTEXTindicates an initial null context. Because gss_init_sec_context() is usually called in a loop, subsequent calls should pass the context handle that was returned by previous calls. -
input_token – The context token received from the client.
The full set of gss_accept_sec_context() arguments is described in the following paragraphs.
Security context establishment might require several handshakes. The initiator and acceptor often need to send more than one piece of context information before the context is fully established. Therefore, for portability, context acceptance should always be done as part of a loop that checks whether the context has been fully established. If the context is not yet established, gss_accept_sec_context() returns a major status code of GSS_C_CONTINUE_NEEDED. Therefore, a loop should use the value that was returned by gss_accept_sec_context() to test whether to continue the acceptance loop.
The context acceptor returns context information to the initiator in
the form of the output token that was returned by gss_accept_sec_context(). Subsequently, the acceptor can receive additional information
from the initiator as an input token. The input token is then passed as an
argument to subsequent gss_accept_sec_context() calls.
When gss_accept_sec_context() has no more tokens to send
to the initiator, an output token with a length of zero is returned. Besides
checking for the return status gss_accept_sec_context(),
the loop should check the output token's length to see whether another token
must be sent. Before the loop begins, the output token's length should be
initialized to zero. Either set the output token to GSS_C_NO_BUFFER,
or set the structure's length field to a value of zero.
The following pseudocode demonstrates an example of context establishment from the server side.
context = GSS_C_NO_CONTEXT
output token = GSS_C_NO_BUFFER
do
receive an input token from the initiator
call gss_accept_sec_context(context, cred handle, input token,
output token, other args...)
if (there's an output token to send to the initiator)
send the output token to the initiator
release the output token
if (there's a GSS-API error)
delete the context
until the context is completeA real loop would be more complete with more extensive error-checking. See Establishing a Security Context With the Server for a real example of such a context-acceptance loop. Additionally, the gss_accept_sec_context() man page provides an example.
Again, GSS-API does not send or receive tokens. Tokens must be handled by the application. Examples of token-transferring functions are found in Miscellaneous GSS-API Sample Functions.
gss_accept_sec_context() returns GSS_S_COMPLETE if it completes successfully. If the context is not complete, the function returns GSS_S_CONTINUE_NEEDED. If errors occur, the function returns error codes. For more information, see the gss_accept_sec_context(3GSS) man page.
Using Other Context Services in GSS-API
The gss_init_sec_context() function enables an application to request additional data protection services beyond basic context establishment. These services are requested through the req_flags argument to gss_init_sec_context().
Not all mechanisms offer all these services. The ret_flags argument for gss_init_sec_context() indicates which services are available in a given context. Similarly, the context acceptor examines the ret_flags value that is returned by gss_accept_sec_context() to determine the available services. The additional services are explained in the following sections.
Delegating a Credential in GSS-API
If permitted, a context initiator can request that the context acceptor act as a proxy. In such a case, the acceptor can initiate further contexts on behalf of the initiator.
Suppose someone on Machine A wants to rlogin to Machine B, and then rlogin from Machine B to Machine C. Depending on the mechanism, the delegated credential identifies B either as A or B as proxy for A.
If delegation is permitted, ret_flags can be set to GSS_C_DELEG_FLAG. The acceptor receives a delegated credential as the delegated_cred_handle argument of gss_accept_sec_context(). Delegating a credential is not the same as exporting a context. See Exporting and Importing Contexts in GSS-API. One difference is that an application can delegate that application's credentials multiple times simultaneously, while a context can only be held by one process at a time.
Performing Mutual Authentication Between Peers in GSS-API
A user who transfers files to an ftp site typically does not need proof of the site's identity. On the other hand, a user who is required to provide a credit card number to an application would want definite proof of the receiver's identity. In such a case, mutual authentication is required. Both the context initiator and the acceptor must prove their identities.
A context initiator can request mutual authentication by setting the gss_init_sec_context() req_flags argument
to the value GSS_C_MUTUAL_FLAG. If mutual authentication has
been authorized, the function indicates authorization by setting the ret_flags argument to this value. If mutual authentication is
requested but not available, the initiating application is responsible for
responding accordingly. GSS-API does not automatically terminate a context
when mutual authentication is requested but unavailable. Also, some mechanisms
always perform mutual authentication even without a specific request.
Performing Anonymous Authentication in GSS-API
In normal use of GSS-API, the initiator's identity is made available to the acceptor as a part of context establishment. However, a context initiator can request that its identity not be revealed to the context acceptor.
For example, consider an application that provides unrestricted access to a medical database. A client of such a service might want to authenticate the service. This approach would establish trust in any information that is retrieved from the database. The client might not want to expose its identity due to privacy concerns, for example.
To request anonymity, set the req_flags argument of gss_init_sec_context() to GSS_C_ANON_FLAG. To verify whether anonymity is available, check the ret_flags argument to gss_init_sec_context() or gss_accept_sec_context() to see whether GSS_C_ANON_FLAG is returned.
When anonymity is in effect, calling gss_display_name() on a client name that was returned by gss_accept_sec_context() or gss_inquire_context() produces a generic anonymous name.
Note –
An application has the responsibility to take appropriate action if anonymity is requested but not permitted. GSS-API does not terminate a context in such a case.
Using Channel Bindings in GSS-API
For many applications, basic context establishment is sufficient to assure proper authentication of a context initiator. In cases where additional security is desired, GSS-API offers the use of channel bindings. Channel bindings are tags that identify the particular data channel that is used. Specifically, channel bindings identify the origin and endpoint, that is, the initiator and acceptor of the context. Because the tags are specific to the originator and recipient applications, such tags offer more proof of a valid identity.
Channel bindings are pointed to by the gss_channel_bindings_t data type, which is a pointer to a gss_channel_bindings_struct structure as shown below.
typedef struct gss_channel_bindings_struct {
OM_uint32 initiator_addrtype;
gss_buffer_desc initiator_address;
OM_uint32 acceptor_addrtype;
gss_buffer_desc acceptor_address;
gss_buffer_desc application_data;
} *gss_channel_bindings_t;
The first two fields are the address of the initiator and an address
type that identifies the format in which the initiator's address is being
sent. For example, initiator_addrtype might be
sent to GSS_C_AF_INET to indicate that initiator_address is in the form of an Internet address, that is, an IP address.
Similarly, the third and fourth fields indicate the address and address type
of the acceptor. The final field, application_data,
can be used by the application as needed. Set application_data to GSS_C_NO_BUFFER if application_data is not
going to be used. If an application does not specify an address, that application
should set the address type field to GSS_C_AF_NULLADDR. The Address Types for Channel Bindings section
has a list of valid address type values.
The address types indicate address families rather than specific addressing formats. For address families that contain several alternative address forms, the initiator_address and acceptor_address fields must contain sufficient information to determine which form is used. When not otherwise specified, addresses should be specified in network byte-order, that is, native byte-ordering for the address family.
To establish a context that uses channel bindings, the input_chan_bindings argument for gss_init_sec_context() should point to an allocated channel bindings structure. The structure's fields are concatenated into an octet string, and a MIC is derived. This MIC is then bound to the output token. The application then sends the token to the context acceptor. After receiving the token, the acceptor calls gss_accept_sec_context(). See Accepting a Context in GSS-API for more information. gss_accept_sec_context() calculates a MIC for the received channel bindings. gss_accept_sec_context() then returns GSS_C_BAD_BINDINGS if the MIC does not match.
Because gss_accept_sec_context() returns the transmitted channel bindings, an acceptor can use these values to perform security checking. For example, the acceptor could check the value of application_data against code words that are kept in a secure database.
Note –
An underlying mechanism might not provide confidentiality for channel binding information. Therefore, an application should not include sensitive information as part of channel bindings unless confidentiality is ensured. To test for confidentiality, an application can check the ret_flags argument of gss_init_sec_context() or gss_accept_sec_context(). The values GSS_C_CONF_FLAG and GSS_C_PROT_READY_FLAG indicate confidentiality. See Initiating a Context in GSS-API or Accepting a Context in GSS-API for information on ret_flags.
Individual mechanisms can impose additional constraints on the addresses
and address types that appear in channel bindings. For example, a mechanism
might verify that the initiator_address field of
the channel bindings to be returned to gss_init_sec_context().
Portable applications should therefore provide the correct information for
the address fields. If the correct information cannot be determined, then GSS_C_AF_NULLADDR should be specified as the address types.
Exporting and Importing Contexts in GSS-API
GSS-API provides the means for exporting and importing contexts. This ability enables a multiprocess application, usually the context acceptor, to transfer a context from one process to another. For example, an acceptor might have one process that listens for context initiators and another that uses the data that is sent in the context. The Using the test_import_export_context() Function section shows how a context can be saved and restored with these functions.
The function gss_export_sec_context() creates
an interprocess token that contains information about the exported context.
See Interprocess Tokens in GSS-API for
more information. The buffer to receive the token should be set to GSS_C_NO_BUFFER before gss_export_sec_context() is called.
The application then passes the token on to the other process. The new process accepts the token and passes that token to gss_import_sec_context(). The same functions that are used to pass tokens between applications can often be used to pass tokens between processes as well.
Only one instantiation of a security process can exist at a time. gss_export_sec_context() deactivates the exported context and sets
the context handle to GSS_C_NO_CONTEXT. gss_export_sec_context() also deallocates any process-wide resources that are associated
with that context. If the context exportation cannot be completed, gss_export_sec_context() leaves the existing security context unchanged and does not return
an interprocess token.
Not all mechanisms permit
contexts to be exported. An application can determine whether a context can
be exported by checking the ret_flags argument
to gss_accept_sec_context() or gss_init_sec_context().
If this flag is set to GSS_C_TRANS_FLAG, then the context can
be exported. (See Accepting a Context in GSS-API and Initiating a Context in GSS-API.)
Figure 4–6 shows how a multiprocess acceptor might use context exporting to multitask. In this case, Process 1 receives and processes tokens. This step separates the context-level tokens from the data tokens and passes the tokens on to Process 2. Process 2 deals with data in an application-specific way. In this illustration, the clients have already obtained export tokens from gss_init_sec_context(). The clients pass the tokens to a user-defined function, send_a_token(), which indicates whether the token to be transmitted is a context-level token or a message token. send_a_token() transmits the tokens to the server. Although not shown here, send_a_token() would presumably be used to pass tokens between threads as well.
Figure 4–6 Exporting Contexts: Multithreaded Acceptor Example
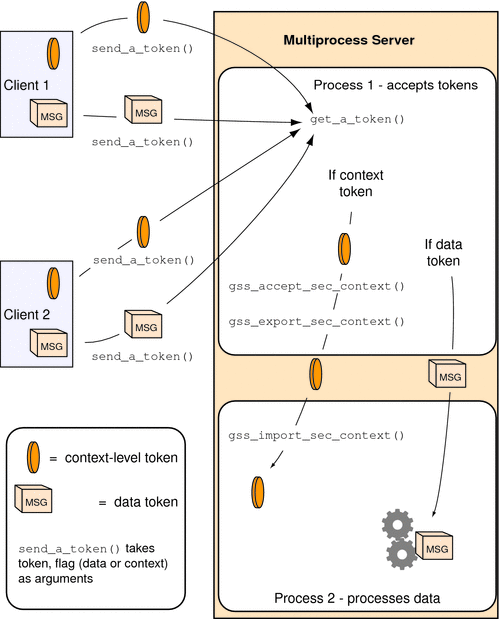
Obtaining Context Information in GSS-API
GSS-API provides a function, gss_inquire_context(3GSS), that obtains information about a given security context. Note that the context does not need to be complete.
Given a context handle, gss_inquire_context() provides the following information about context:
-
Name of the context initiator.
-
Name of the context acceptor.
-
Number of seconds for which the context is valid.
-
Security mechanism to be used with the context.
-
Several context-parameter flags. These flags are the same as the ret_flags argument of the gss_accept_sec_context(3GSS) function. The flags cover delegation, mutual authentication, and so on. See Accepting a Context in GSS-API.
-
A flag that indicates whether the inquiring application is the context initiator.
-
A flag that indicates whether the context is fully established.
Sending Protected Data in GSS-API
After a context has been established between two peers, a message can be protected before that message is sent.
Establishing a context only uses the most basic GSS-API protection: authentication. Depending on the underlying security mechanisms, GSS-API provides two other levels of protection:
-
Integrity – A message integrity code (MIC) for the message is generated by the gss_get_mic() function. The recipient checks the MIC to ensure that the received message is the same as the message that was sent.
-
Confidentiality – In addition to using a MIC, the message is encrypted. The GSS-API function gss_wrap() performs the encryption.
The difference between gss_get_mic() and gss_wrap() is illustrated in the following diagram. With gss_get_mic(), the receiver gets a tag that indicates the message is intact. With gss_wrap(), the receiver gets an encrypted message and a tag.
Figure 4–7 gss_get_mic() versus gss_wrap()
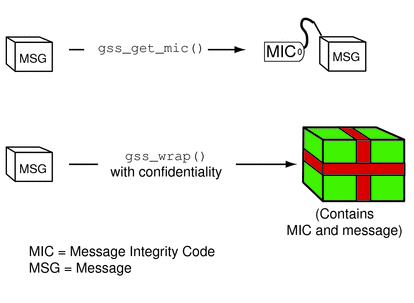
The function to be used depends on the situation. Because gss_wrap() includes the integrity service, many programs use gss_wrap(). A program can test for the availability of the confidentiality service. The program can then call gss_wrap() with or without confidentiality depending on the availability. An example is Wrapping and Sending a Message. However, because messages that use gss_get_mic() do not need to be unwrapped, fewer CPU cycles are used than withgss_wrap(). Thus a program that does not need confidentiality might protect messages with gss_get_mic().
Tagging Messages With gss_get_mic()
Programs can use gss_get_mic() to add a cryptographic MIC to a message. The recipient can check the MIC for a message by calling gss_verify_mic().
In contrast to gss_wrap(), gss_get_mic() produces separate output for the message and the MIC. This separation means that a sender application must arrange to send both the message and the accompanying MIC. More significantly, the recipient must be able to distinguish between the message and the MIC.
The following approaches ensure the proper processing of message and MIC:
-
Through program control, that is, state. A recipient application might know to call the receiving function twice, once to get a message and a second time to get the message's MIC.
-
Through flags. The sender and receiver can flag the kind of token that is included.
-
Through user-defined token structures that include both the message and the MIC.
GSS_S_COMPLETE is returned if gss_get_mic() completes successfully. If the specified QOP is not valid, GSS_S_BAD_QOP is returned. For more information, see gss_get_mic(3GSS).
Wrapping Messages With gss_wrap()
Messages can be wrapped by the gss_wrap() function. Like gss_get_mic(), gss_wrap() provides a MIC. gss_wrap() also encrypts a given message if confidentiality is requested and permitted by the underlying mechanism. The message receiver unwraps the message with gss_unwrap().
Unlike gss_get_mic(), gss_wrap() wraps the message and the MIC together in the outgoing message. The function that transmits the bundle need be called only once. On the other end, gss_unwrap() extracts the message. The MIC is not visible to the application.
gss_wrap() returns GSS_S_COMPLETE if the message was successfully wrapped. If the requested QOP is not valid, GSS_S_BAD_QOP is returned. For an example of gss_wrap(), see Wrapping and Sending a Message.
Handling Wrap Size Issues in GSS-API
Wrapping a message with gss_wrap() increases the amount of data to be sent. Because the protected message packet needs to fit through a given transportation protocol, GSS-API provides the function gss_wrap_size_limit(). gss_wrap_size_limit() calculates the maximum size of a message that can be wrapped without becoming too large for the protocol. The application can break up messages that exceed this size before calling gss_wrap(). Always check the wrap-size limit before actually wrapping the message.
The amount of the size increase depends on two factors:
-
Which QOP algorithm is used for making the transformation
-
Whether confidentiality is invoked
The default QOP can vary from one implementation of GSS-API to another. Thus, a wrapped message can vary in size even if the QOP default is specified. This possibility is illustrated in the following figure.
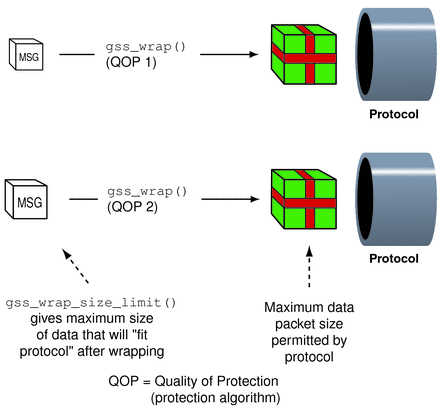
Regardless of whether confidentiality is applied, gss_wrap() still increases the size of a message. gss_wrap() embeds a MIC into the transmitted message. However, encrypting the message can further increase the size. The following figure shows this process.
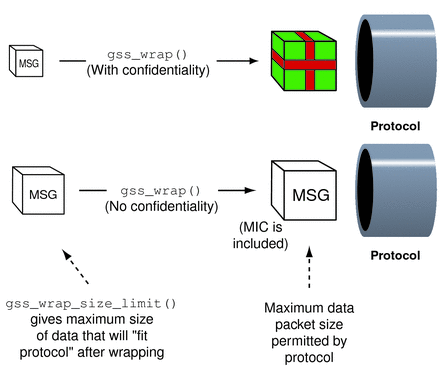
GSS_S_COMPLETE is returned if gss_wrap_size_limit() completes successfully. If the specified QOP is not valid, GSS_S_BAD_QOP is returned. Wrapping and Sending a Message includes an example of how gss_wrap_size_limit() can be used to return the maximum original message size.
Successful completion of this call does not necessarily guarantee that gss_wrap() can protect a message of length max-input-size bytes. This ability depends on the availability of system resources at the time that gss_wrap() is called. For more information, see the gss_wrap_size_limit(3GSS) man page.
Detecting Sequence Problems in GSS-API
As a context initiator transmits sequential data packets to the acceptor, some mechanisms allow the context acceptor to check for proper sequencing. These checks include whether the packets arrive in the right order, and with no unwanted duplication of packets. See following figure. An acceptor checks for these two conditions during the verification of a packet and the unwrapping of a packet. See Unwrapping the Message for more information.
Figure 4–8 Message Replay and Message Out-of-Sequence

With gss_init_sec_context(), an initiator can check
the sequence by applying logical OR to the req_flags argument with either GSS_C_REPLAY_FLAG or GSS_C_SEQUENCE_FLAG.
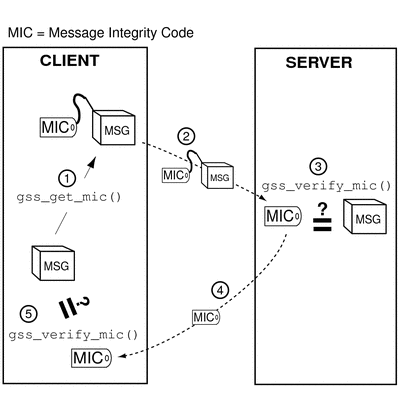
Confirming Message Transmission in GSS-API
After the recipient has unwrapped or verified the transmitted message, a confirmation can be returned to the sender. This means sending back a MIC for that message. Consider the case of a message that was not wrapped by the sender but only tagged with a MIC with gss_get_mic().
-
The initiator tags the message with gss_get_mic().
-
The initiator sends the message and MIC to the acceptor.
-
The acceptor verifies the message with gss_verify_mic().
-
The acceptor sends the MIC back to the initiator.
-
The initiator verifies the received MIC against the original message with gss_verify_mic().
The process, illustrated in Figure 4–9, is as follows:
Figure 4–9 Confirming MIC Data
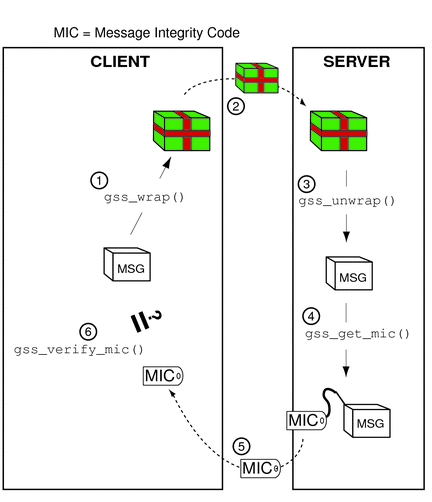
In the case of wrapped data, the gss_unwrap() function never produces a separate MIC, so the recipient must generate it from the received and unwrapped message.
-
The initiator wraps the message with gss_wrap().
-
The initiator sends the wrapped message.
-
The acceptor unwraps the message with gss_unwrap().
-
The acceptor calls gss_get_mic() to produce a MIC for the unwrapped message.
-
The acceptor sends the derived MIC to the initiator.
-
The initiator compares the received MIC against the original message with gss_verify_mic().
The process, illustrated in Figure 4–10, is as follows:
Applications should deallocate any data space that has been allocated for GSS-API data. The relevant functions are gss_release_buffer(3GSS), gss_release_cred(3GSS), gss_release_name(3GSS), and gss_release_oid_set(3GSS).
Figure 4–10 Confirming Wrapped Data
Cleaning Up a GSS-API Session
Finally, all messages have been sent and received, and the initiator and acceptor applications have finished. At this point, both applications should call gss_delete_sec_context() to destroy the shared context. gss_delete_sec_context() deletes local data structures that are associated with the context.
For good measure, applications should be sure to deallocate any data space that has been allocated for GSS-API data. The functions that do this are gss_release_buffer(), gss_release_cred(), gss_release_name(), and gss_release_oid_set().
- © 2010, Oracle Corporation and/or its affiliates
