3.5 加速

如果编译器不并行化所花时间量占主体的程序部分，则不会发生加速。这基本上是 Amdahl 定律的推论。例如，如果并行化一个占用程序执行时间的百分之五的循环，则总加速仅限于百分之五。然而，根据工作量和并行执行开销的大小，可能没有任何改善。

一般说来，并行化的程序执行所占的比例越大，加速的可能性就越大。

每个并行循环都会在启动和关闭期间发生少量开销。启动开销包括工作分配代价，关闭开销包括障碍同步代价。如果循环执行的工作总量不足够大，则不会发生加速。事实上，循环甚至可能减慢。因此，如果大量程序执行工作由许多短并行循环完成，则整个程序可能减慢而不是加速。

编译器执行几个试图增大循环粒度的循环变换。其中某些变换是循环交换和循环合并。因此，一般说来，如果程序中的并行量很小或者分散在小并行区域，则加速很少。

通常，按比例增大问题大小可提高程序中的并行程度。例如，考虑包含以下两部分的问题： 按顺序的二次部分，以及可并行化的三次部分。对于此问题，工作量的并行部分的增长速度比顺序部分的增长速度快。因此在某些点，除非达到资源限制，否则问题可以大大加速。

尝试进行某些调节，使用指令、问题大小进行试验，重新构造程序，以便从并行 C 中获益。

3.5.1 Amdahl 定律

固定问题大小加速通常遵守 Amdahl 定律。Amdahl 定律仅仅指出一个给定问题中的并行加速量受此问题的顺序部分限制。下面的公式介绍了某个问题的加速，其中 F 是花在顺序区域的时间部分，其余的时间部分则均匀地分布于 P 个处理器。如果方程式的第二项减小到零，则总加速受第一项约束，保持固定。

下图以图表方式说明此概念。深色阴影部分表示程序的顺序部分，并且对于 1、2、4、8 个处理器均保持不变。浅色阴影部分代表程序的并行部分，可均匀地分摊在任意多个处理器之间。

图 3-3 固定问题加速

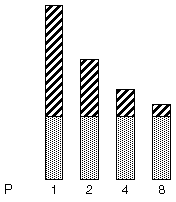
随着处理器数目的增加，每个程序并行部分所需的时间会减少，而每个程序串行部分所需的时间保持不变。

然而，实际上可能会发生由于通信以及向多个处理器分配工作而产生的开销。对于使用的任意多个处理器，这些开销可能固定，也可能不固定。

下图说明一个包含 0%、2%、5% 和 10% 顺序部分的程序的理想加速。此处假定无开销。

图 3-4 Amdahl 定律加速曲线

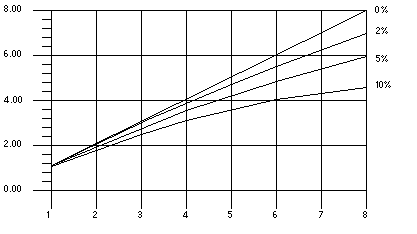
显示一个包含 0%、2%、5% 和 10% 顺序部分的程序的理想加速（假定无开销）的图。x 轴表示处理器的数目，y 轴表示加速。

3.5.1.1 开销

一旦将开销加入此模型中，加速曲线会发生很大的变化。为了方便说明，我们假定开销包括以下两部分： 独立于处理器数的固定部分，以及随使用的处理器数呈二次增长的非固定部分：

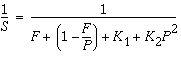
1 除以 S 等于 1 除以下列数值之和：F 加上左括号 1 减去 F 除以 P 右括号加上 K（下标 1）加上 K（下标 2）乘以 P 的平方。

在此方程式中，K₁ 和 K₂ 是固定因子。在这些假定下，加速曲线如下图所示。值得注意的是，在此情况下，加速达到峰值。在某个点之后，增加更多处理器会降低性能，如下图所示。

图 3-5 带开销的加速曲线

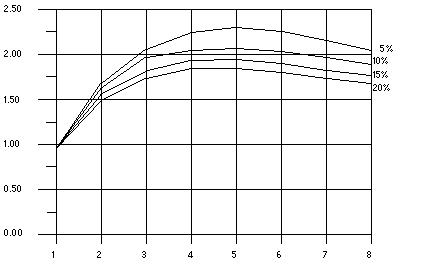
此图显示：使用 5 个处理器时所有程序到达最高加速，然后添加到多达 8 个处理器时即会失去此加速优势。x 轴表示处理器的数目，y 轴表示加速。

3.5.1.2 Gustafson 定律

Amdahl 定律可能会在预测真实问题的并行加速时造成误导。花费在程序的顺序部分的时间有时取决于问题大小。也就是说，通过按比例缩放问题大小，您可以获得更多加速机会。以下示例说明了这一点。

示例 3-12 按比例缩放问题大小可能会获得更多加速机会

/*
* initialize the arrays
*/
for (i=0; i < n; i++) {
    for (j=0; j < n; j++) {
            a[i][j] = 0.0;
            b[i][j] = ...
            c[i][j] = ...
    }
}
/*
* matrix multiply
*/
for (i=0; i < n; i++) {
    for(j=0; j < n; j++) {
            for (k=0; k < n; k++) {
                a[i][j] = b[i][k]*c[k][j];
            }
    }
}

假定理想的开销为零，并假定只有第二个循环嵌套并行执行。不难发现，对于较小的问题大小（即 n 的值较小），程序的顺序部分和并行部分所用的时间彼此相差并不大。然而，随着 n 值的增大，花费在程序并行部分的时间比花费在顺序部分的时间增长得更快。对于此问题，随问题大小的增大而增加处理器数很有益。