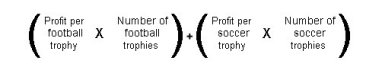Supply Chain Network Optimization Overview
This chapter covers the following topics:
- Introduction to Strategic Network Optimization
- Introduction to Models
- Optimal Model Solutions
- Solutions for Business Problems
Introduction to Strategic Network Optimization
To solve a business problem in Strategic Network Optimization, you use a model that represents your supply chain network through any planning horizon. In the model, you can enter data that represents costs and constraints in your supply chain network.
After entering data in a supply chain network model, you can solve the model. When you solve a model, the Strategic Network Optimization solver balances the conflicting objectives and limitations of supply, production, and distribution in the model and determines how to meet demand with the least cost or with the most profit.
After solving a model, you can extract data, produce reports, and analyze the results. With the report writing and geographical mapping capabilities of Strategic Network Optimization, you can create customized reports and graphically represent your plans and the supply chain network.
You can model and solve your supply chain network using the graphical user interface in Strategic Network Optimization, or automate these processes using Import and Batch commands.
Introduction to Models
Nodes
Nodes represent points in your supply chain network that store, process, or demand resources or materials. For example, nodes can represent suppliers that provide raw materials, production lines that process materials, or distributors that require finished goods. There are many types of nodes in Strategic Network Optimization. Each node type includes different data fields, enabling you to model diverse operations in your supply chain.
For example, Storage node data fields represent commodity storage levels, costs, and constraints. Machine node data fields describe the amount of time available on the machine and the amount of time required for setup.
You can use nodes to:
-
Model storage. For example, nodes can represent warehouses that supply materials or finished products.
-
Model processing. For example, nodes can represent production lines that blend commodities, separate commodities, or package finished goods.
-
Control commodity flows. Nodes can add time, cost, and other commodity flow constraints to a model.
-
Organize models. For example, nodes can group related nodes in a model.
Nodes appear as rectangles on a model. Each rectangle contains a symbol and a name. The symbol represents the node type, and the name identifies the node.
Commodities
Commodities represent materials and resources that are created or consumed in your supply chain network. Commodities can include raw materials, work in progress, finished products, or time. Typically, each model includes several commodities. For example, a model that represents a pancake production line could include the following commodities:
-
Flour (raw material)
-
Sugar (raw material)
-
Flavoring (raw material)
-
Pancake mix (work in progress)
-
Packaged pancake mix (finished good)
-
Time available on a blending or packaging machine
Commodities flow into and out of nodes through arcs and attach points. At each node something happens to the commodity, as specified by the kind of node and data in the node. To view the commodities in a model, you must open the Commodities window.
Three commodities exist in every Strategic Network Optimization model and cannot be edited or deleted: Promotions, Reserved Time, and Storage Level. Promotions are used with Promotion nodes. Reserved time is used with Batch, Machine, and MachineDelta nodes. Storage level is used with nodes that model storage. You must define any other commodities that are created or consumed in your supply chain model.
Arcs and Attach Points
Arcs represent the flow of commodities between operations in a supply chain network. Each arc carries one commodity between nodes. Arc colors indicate the direction of the commodity flow: commodities flow from the dark end of arcs to the lighter end.
Arc fields enable you to represent the amount of commodity flowing between two operations or facilities, the possible reduction to the overall cost that results from a unit increase in the minimum or maximum flow, cost of moving the commodity between the nodes, and the minimum and maximum amounts of commodity that should flow through the arc.
Arcs connect to nodes at attach points. Attach points represent the points where commodities flow into or out of a supply chain operation. An attach point on the left side of a node indicates that a commodity is entering the operation. An attach point on the right side indicates that a commodity is exiting the node. Some nodes have more than one input or output attach point.
One commodity is specified for each attach point. An arc can join attach points on two nodes if the same commodity is specified for both attach points.
Time Periods
Time periods define the planning horizon of your model. A model can have one or more time periods. Each time period can represent a different length of time. For example, one model can include both one-week and one-month periods.
Models have the same nodes, arcs, and structure in every time period. However, the data in nodes and arcs can change in each period to reflect changes in costs, constraints, and commodity flows. For example, an arc can carry 150 units of a commodity in one time period, 200 units of the commodity in another period, and 170 units in another.
Supply Chain Data
Nodes and arcs contain numerical data that represents capacities, costs, and constraints in a supply chain network. For example, arcs include data that describes the amount of a commodity flowing through the arc and the minimum and maximum amounts of a commodity that can flow through the arc. A node or arc can have different data values in each time period.
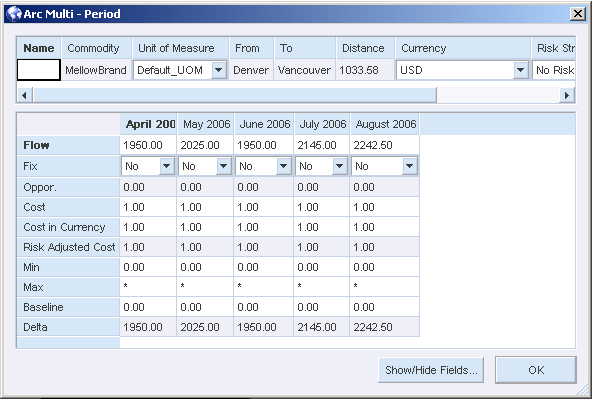
You cannot see supply chain data in the main Strategic Network Optimization window. You must browse, query, or extract the numerical data to view it. The example below shows data for an Arc in a multi-period properties window:
Each node type includes different data that models costs and constraints for different operations. For example, a Storage node can model a warehouse or facility that stores a commodity and include data describing the amount of commodity stored at the facility.
You can view or change supply chain data in the properties window. You can change data in multiple nodes and arcs using change windows or you can import supply chain data in batch mode.
Optimal Model Solutions
After you use Strategic Network Optimization to create your supply chain network model, you can optimize the model. By optimizing your model, you can determine the following:
-
The least expensive way to meet the demand in your supply chain network model
-
The best way to meet customer demand in your supply chain network
-
The optimal quantities of inventory to keep costs at a minimum while maximizing customer service levels
-
The best procurement, manufacturing, and distribution plans for new product lines
-
Where to locate plants, warehouses, and other critical resources
You can also use the Strategic Network Optimization solver to solve other business problems. For example, you can decide what facilities or other assets to open or close and when to do so. You can also determine the best way to meet demand in your supply chain network under various constraints, such as the following:
-
Restricting supply to a single source
-
Limiting the number of commodities that can flow through a particular facility
-
Respecting batch sizes or minimum run lengths
-
Limiting change in the amount of a supplied commodity
You can solve the model to determine least-cost method for meeting product demand in your supply chain network based on the costs and constraints in the supply chain network data in your model.
The software balances the conflicting objectives and limitations of supply, production, and distribution. The Strategic Network Optimization solver uses advanced linear programming techniques to find the optimal solution with the lowest cost. To find the optimal solution for a model, the system converts the constraints, variables and costs from Min fields, Max fields, Cost fields, and Over Cost fields in a model into a linear programming matrix (.mps file), solves the matrix, and fills in values in all of the calculated fields in the nodes and arcs of the model.
The following example shows how linear programming can solve a business problem. After the case is solved graphically, a sample model is provided to show how the problem can be modeled and solved using the Strategic Network Optimization system. Models that represent real world business processes are more complex and have many more variables. However, using the conceptual approach shown in this example, the system can model and optimize the processes used in many industries.
Optimal Model Solution Example
A company that makes championship trophies for youth athletic leagues is planning trophy production for two sports: football and soccer. Each football trophy has a wood base, an engraved plaque, and a large brass football on top. Each soccer trophy is the same, except that it has a brass football on top instead of a soccer ball. Each soccer trophy requires 2 board feet of wood for the base. Since the football is asymmetrical, each football trophy requires 4 board feet of wood. Each football trophy returns 12 USD profit, and each soccer trophy returns 9 USD profit.
The planner has checked the company's inventory and found the following materials in stock:
-
1000 brass footballs
-
1500 brass soccer balls
-
1750 plaques
-
4800 board feet of wood
What trophies should be produced from the available supplies to maximize total profit? The two values we need to find a solution for are:
x = the number of football trophies to produce
y = the number of soccer trophies to produce
The objective function is to maximize profit. Profit can be defined as:
Expressed in variable terms, this problem is 12x + 9y. The constraints in the problem are as follows:
-
Only 1000 brass footballs are in stock, so no more than 1000 football trophies can be produced. In variable terms, x <= 1000 and x >= 0.
-
Only 1500 brass soccer balls are in stock, so no more than 1500 soccer trophies can be produced. In variable terms, y <= 1500 and y >= 0.
-
Only 1750 plaques are in stock, so the total number of trophies produced cannot be more than 1750. In variable terms, x + y <= 1750.
-
Only 4800 board feet of wood is available, so the total number of trophies produced cannot consume more than 4800 board feet of wood. In variable terms, 4 x + 2 y <= 4800.
The linear program is as follows:
Maximize 12 x + 9 y
where 0 <= x <= 1000
0 <= y <= 1500
x + y <= 1750
4 x + 2 y <= 4800
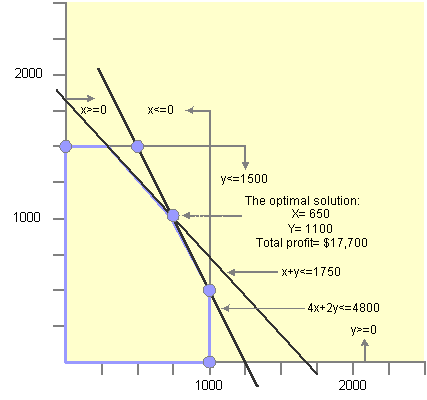
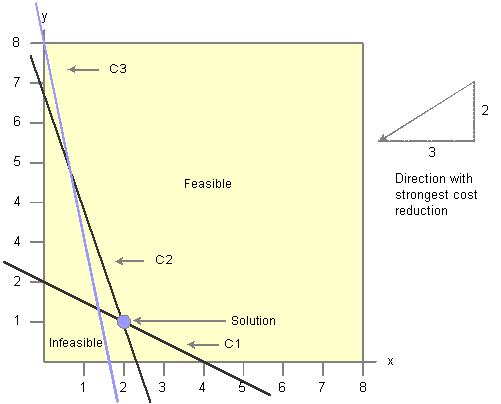
The example is graphed below. The vertex (650, 1100) is the point that provides the best solution, with a total profit of 17,700 USD. In other words, 650 football trophies and 1100 soccer trophies should be made to maximize profit, given the constraints of the available supplies.
The Basics of Linear Programming
When you model and solve the problem using linear programming in Strategic Network Optimization, you obtain the same solution as discussed above. The model that represents this problem includes only one time period. The six commodities in the model are:
-
Brass soccer balls
-
Brass footballs
-
Plaques
-
Wood
-
Completed soccer trophies
-
Completed football trophies
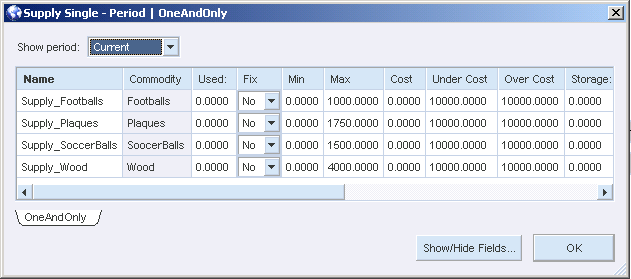
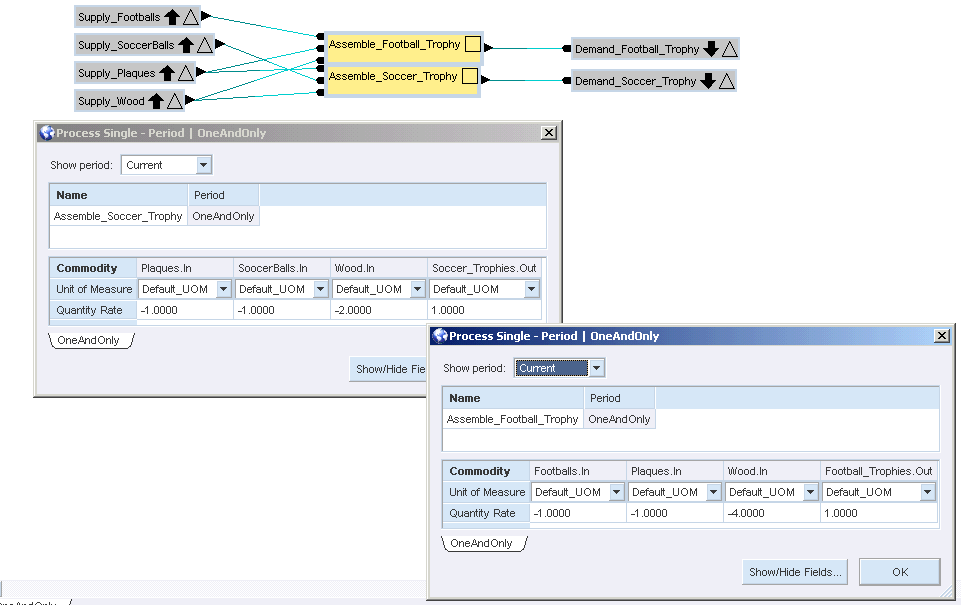
The basic structure of the model is to assemble the trophies. Every model requires supply and demand, so those nodes need to be modeled as well. The supply nodes are modeled as follows:
The values in the Maximum field represent the total number of each commodity available and is the only field used. The supply nodes feed into two process nodes to represent the assembly process:
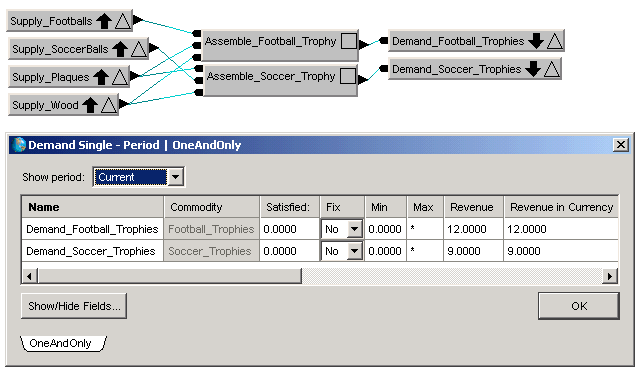
Note that the football trophies use 4 units of wood each, and the soccer trophies use only 2. Also note which commodities flow into the assembly process nodes. To complete the model, the demand nodes are created:
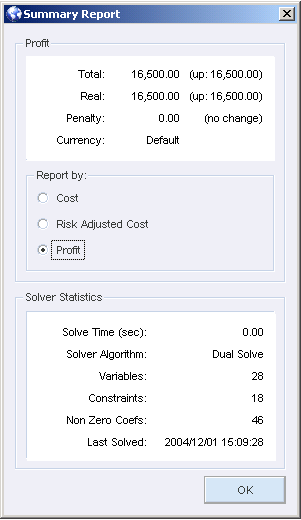
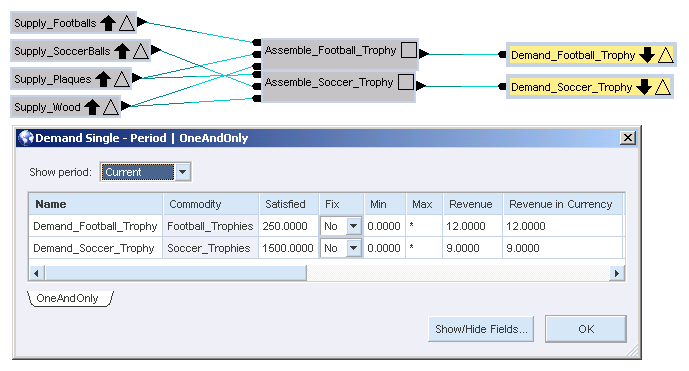
After entering all the data, you can run the solve. Completion of the solve is nearly instantaneous. The Summary report shows the Profit as 16,500 the same solution found in the graphical approach.
You can view the properties window for the Demand nodes (in the Satisfied field) to see that 250 football trophies and 1500 soccer trophies should be made.
Linear Programming Algorithms
The system can use a number of different algorithms to solve the linear programming formulation of a model. The algorithm you select depends on many factors, such as the structure of the model, its constraints and variables, and its size. Determining which one is best for a particular model might require extensive testing, and should be done under the guidance of an expert.
Summary of Linear Programming Algorithms
The following table displays a summary of linear programming algorithms:
| Algorithm | Speed of First Time Solve | Speed of Second Solve | Interruption | Infeasibility Information |
|---|---|---|---|---|
| Primal | + | +++ | Basis stored for primal re-solve. Feasible solution if in phase 2. | If the model is infeasible, a set of elements that cause the infeasibility is created. |
| Dual | ++ | +++ | Basis stored for dual re-solve. | When the model is infeasible, the Dual solver reports that the problem is unbounded. |
| Network basis then primal* | ++ | - | Basis stored for use in primal simplex resolve. Feasible solution if in phase 2. | The network extractor gives an error message with the constraint or variable that causes infeasibility. Use the constraint and variable finders to find the associated elements. |
| Network basis then dual*. | ++ | - | Basis stored. Use dual simplex algorithm to re-solve with this basis | The network extractor gives an error message with the constraint or variable that causes infeasibility. Use the constraint and variable finders to find the associated elements. |
| Barrier | +++ | - | No new basis stored. | If the model is infeasible, a set of elements that cause the infeasibility is created. |
+++ = faster + = slower. * Network algorithms are not guaranteed to work with all models.
Primal Simplex Algorithm
The primal simplex algorithm optimizes the primal formulation of the linear programming by iteratively moving from a feasible basis to an improved feasible basis. The algorithm terminates when it is guaranteed that a better basis does not exist.
The primal simplex algorithm needs a primal feasible basis to begin. The process of finding the initial primal feasible basis is called phase 1 of the simplex method. The primal simplex algorithm solves in two phases:
-
Finds a primal feasible basis
-
Keeps improving the primal feasible basis until the lowest cost primal feasible basis is found
Phase 1 introduces artificial slack variables to transform the original linear programming to related linear programming that automatically has a feasible basis. The goal is then to change the basis until these artificial slack variables have been removed from the basis.
The cost of a solution to the phase 1 problem is also called the infeasibility measure. When the infeasibility measure reaches 0, the solver has found a primal feasible basis without needing the artificial slack variables. On this basis, phase 2 begins when the basis for the original problem is improved.
The primal simplex algorithm has the following characteristics:
-
Once phase 2 is entered, the solution is primal feasible. If the solve is cancelled in this phase, a feasible solution to the linear programming is stored in the model, although the solution is not optimal.
-
If the optimal value of the phase 1 problem is greater than zero, linear programming is infeasible. If this is the case, the information from the phase 1 problem is used to create an Infeasible user set that contains the elements that together cause an infeasibility. This set can be analyzed with the set browser.
-
The solve time can often be reduced by installing the basis from the most recent solve and optimizing from that basis. If the structure of a model and the data did not change significantly, the new basis will be very close to the optimal basis and the model can be solved again quickly.
-
If the data changes significantly, you should discard the basis before re-solving.
Dual Simplex Algorithm
The dual simplex algorithm, like the primal simplex, improves the basis of a linear programming. However, it optimizes the dual formulation of the linear programming. Like the primal algorithm, it uses a two-phase approach:
-
Finds a feasible basis to the dual problem
-
Improves the basis until an optimal basis to the dual problem is found
The speed of solving a typical model with dual simplex usually is comparable to the speed of solving with primal simplex. Depending on the individual model, it can be marginally faster or slower than primal simplex.
The dual simplex algorithm has the following characteristics:
-
The solution is not primal feasible until the end of the solve. If the solve is canceled, no solution is stored in the model.
-
The algorithm installs the basis from the most recent solve and starts improving that basis. If the structure of a model and its data have not changed significantly, the new basis will be very close to the optimal basis and the model can be solved again quickly. Small changes to a model are likely to affect dual feasibility and the dual simplex algorithm, so it is probably has to do both phase 1 and phase 2. This situation often causes the model to solve again more slowly than with primal simplex. In this case, you should discard the basis.
-
If the problem is primal infeasible, the dual problem is unbounded. No extra information available is about the infeasibilities.
Network Basis Then Primal Algorithm
The network basis then primal algorithm tries to extract a network structure from the linear programming. The network-simplex algorithms (network basis then primal and network basis then dual) are usually much faster than the pure simplex algorithms (primal and dual). After the extracted network problem has been solved, the basis that one gets from this problem is used as a starting point for the primal simplex algorithm.
The network extraction process is not guaranteed to work, even if the linear programming is feasible and has an optimal solution. If the linear programming is infeasible or unbounded, the extraction process fails and a solver error message indicates the constraint or variable where the problem was detected. You can use the Constraint Finder or the Variable Finder to locate the elements in the model that cause the solver to fail.
To open the Constraint Finder, select Find from the Edit menu and then select Constraint Finder.
To open the Variable Finder, select Find from the Edit menu and then select Variable Finder.
The network basis then primal algorithm has the following characteristics:
-
Once phase 2 is entered the solution is primal feasible. If the solve is canceled in this phase no feasible solution to the linear programming in the model exists, although it is not optimal.
-
The network algorithm does not use a previous basis. Solving the model again takes as much time as the original solve
-
Some information about infeasibility can be derived from the Solver System error messages
Network Basis Then Dual Algorithm
The Network Basis Then Dual algorithm uses the network structure of a linear programming, but instead of using primal objectives it uses dual objectives. The Network Basis Then Dual algorithm has the following characteristics:
-
The solution is not feasible until the end of the solve. If the solve is canceled, no solution is stored in the model.
-
The network algorithm does not use a previous basis. Solving the model again takes as much time as the original solve.
-
Some information about infeasibility can be derived from the solver error messages.
Barrier Algorithm
The barrier algorithm is an interior point, nonsimplex algorithm for solving linear programs. In most instances it is the fastest algorithm-possibly three times as fast as the network algorithms. It is more reliable than the network algorithms, which sometimes fail in the network extraction phase.
The barrier algorithm uses fewer, but longer and more complicated, iterations than the simplex and network algorithms. The algorithm starts out with an algebraic (Cholesky) decomposition of the constraint matrix and some time can pass before the first iteration is completed.
The barrier algorithm has the following characteristics:
-
If the solve is canceled, no solution is stored in the model.
-
Solving the model again takes as long as the original solve.
Expert users can configure barrier solver parameters such as:
-
Barrier Iteration Limit - the number of iterations before the barrier solve stops.
-
Barrier Thread Limit - the number of parallel processes that will be invoked by the solver.
Duality and the Linear Programming Basis
This section provides theory about linear programming to offer some insight into the workings of the linear programming solving algorithms. A linear programming problem involves maximizing or minimizing a linear objective function subject to a number of linear constraints.
For example:
-
Cost objective: 3 x + 2 y
-
Constraint C1: 2 x + 5 y = 10
-
Constraint C2: x + 0.4 y = 2.3
-
Constraint C3: x + 0.2 y = 1.6
-
Variable bounds: x = 0, y = 0
The goal in this example is to find values for the decision variables x and y that have the lowest cost objective while satisfying the constraints C1, C2, and C3 as well as the variable bounds.
With only two variables, you can draw the region of x and y variables that satisfy the constraints:
This graphical approach does not work for larger problems, so the general notation of the linear programming is:
with:
Duality
Every linear programming has a related dual linear programming. The dual linear programming of the problem in the general linear programming notation is:
with:
One of the theorems from the field of linear programming states that if x is primal feasible (all the constraints from the primal linear programming are met) and y is dual feasible (all the constraints from the dual linear programming are met) then:
(The value of the objective function in any primal feasible solution is greater or equal to the value of the objective function in all dual feasible solutions.)
Theory shows that the optimal solution to the primal linear programming has the same objective function value as the optimal solution to the dual linear programming. By solving the dual formulation of a linear programming, you can also find an optimal solution to the primal linear programming.
The Linear Programming Basis
A linear programming problem consists of a set of decision variables, a linear objective (cost) function, and a set of linear constraints.
-
Cost: 3 x + 2 y + 3 z
-
Constraint: 2 x + y = 3
-
Constraint: y + z = 2
-
Bounds: x = 0, y = 0, z = 0
A simplex method introduces slack or surplus variables in order to generate equality constraints:
-
Cost: 3 x + 2 y + 3 z
-
Constraint: 2 x + y - s1 = 3
-
Constraint: y + z - s2 = 2
-
Bounds: x = 0, y = 0, z = 0, s1 = 0, s2 = 0
A mathematical theorem states that for linear programming with m constraints (not including constraints which bound the variables), one lowest cost solution exists that needs, at most, m variables to be unequal to one of their bounds.
The optimal result of the linear programming in this example is (x=0.5,y=2,z=0,s1=0,s2=0) with a cost of 5.5. A basis is a set of m variables that are allowed to be unequal to their bounds. In the solution to this problem the basis consists of the variables x and y.
A basis is called primal feasible if the constraints (including bounds) can be satisfied with the variables in the basis.
Simplex and Barrier Solves
The importance of linear programming derives in part from its many applications and in part from the existence of good general purpose techniques for finding optimal solutions. These techniques take only linear programming in the standard form as input, and determine a solution without reference to any information concerning the origins or special structure of linear programming. They are fast and reliable over a substantial range of problem sizes and applications.
Two families of solution techniques are in wide use. Both visit a progressively improving series of trial solutions, until a solution is reached that satisfies the conditions for an optimum.
Simplex methods, introduced about 50 years ago, visit "basic" solutions computed by fixing enough of the variables at their bounds to reduce the constraints Ax=b to a square system, which can be solved for unique values of the remaining variables. Basic solutions represent extreme boundary points of the feasible region defined by Ax=b,x>= 0, and the simplex method can be viewed as moving from one such point to another along the edges of the boundary.
Barrier or interior-point methods, by contrast, visit points within the interior of the feasible region. These methods derive from techniques for nonlinear programming that were developed and popularized in the 1960s, but their application to linear programming dates back only to 1984.
Interior point methods can take a long time to solve for at least two reasons. In general, these methods perform a number of iterations (small relative to simplex), but the work within each iteration is much more extensive than simplex. You have to determine if the number of iterations is "too large" or if the time spent in a single iteration is "too long."
The number of iterations is a function of the linear programming, which is based on the structure of the matrix that is passed to the solver. The solver takes the least amount of iterations possible to reach a solution. The time spent in a single iteration is more likely to depend on the structure of the constraints. The solver determines how long it will take, using the fastest proprietary techniques to reduce this time.
When the work within an iteration becomes less efficient, the bottleneck in the inner iteration is a matrix factorization step. If A is the constraint matrix then the efficiency of the matrix factorization is directly related to the density (number of nonzero elements in) ATA. A great deal of work has been done in speeding up the matrix factorizations (most people use some sort of preconditioned conjugate gradient to compute an incomplete Cholesky factorization).
Relative to the number of iterations, the solver has been optimized to improve the results with proprietary techniques.
The number of nonzeros can affect barrier solve performance. First, when you run the barrier method, the number of nonzeros in the Cholesky factorization of the system of equations that are solved during each barrier iteration are displayed. The more nonzeros, the longer each barrier iteration takes. So a nonzero count of several million nonzeros makes it unlikely that the barrier method will do well. Second, the sparsity structure of the constraint matrix multiplied by its transpose profoundly influences barrier performance. If this matrix has many nonzeros, the resulting Cholesky factorization is probably be dense, resulting in slower performance.
The data structure of linear programming does not disallow solving using the Barrier method like the Network method. Barrier is not dependent on data structure. Barrier does not have data dependencies like Network solves for such things as network extraction. If a model can be solved using a Simplex method, then it can be solved using the barrier method.
Solutions for Business Problems
Pure linear programming solutions are useful for finding the least cost or maximum revenue. However, if you want to achieve goals that do not fit with the least cost solution, you can apply heuristics that use the linear programming structure of the problem to find a feasible and near optimal solution.
Strategic Network Optimization can model many specific business problems that have nonlinear characteristics. Because they are nonlinear, these processes and constraints cannot be modeled as a linear program. The processes that must be addressed by separate heuristics are:
| Process | Node Type | Description |
|---|---|---|
| Capital asset management (asset rationalization) | Block | For modeling the opening or closing of facilities or other assets over a long-term horizon. |
| Single sourcing | Block | All the commodities must come from the same single source node. |
| Limiter | Limiter | Only a limited number of different commodities can flow through this node. |
| Minimum run length | Batch | The flow through the node is either 0 or greater than the minimum run length. |
| Batch size | Batch | The flow through the node is a multiple of the batch size. |
| Load smoothing | MachineDelta | The change in a supplied commodity must be either 0 or greater than a threshold value. |
Addressing these nonlinear processes takes more computational effort than processes that can be modeled with linear constraints. When you build a model, use these processes only when necessary.
Capital Asset Management
Strategic Network Optimization enables you to perform facility analysis on your supply chain, which can have a profound effect in production planning, transportation costs, inventory costs, and product mix. To perform this strategic facility analysis, you can incorporate the Capital Asset Management (CAM) heuristic into your model. By using this heuristic, you can answer any of the following questions:
-
How many facilities (such as plants or distribution centers) should I have?
-
Where should these facilities be located?
-
What impact will offshore operations have on my supply chain?
-
Can the facilities be rationalized, but without compromising the ability to meet demand?
-
How can supply chain risk be mitigated?
-
When should facilities be opened or closed?
The CAM heuristic addresses these questions by simultaneously optimizing the fixed monthly operating cost of facilities and considering the variable cost of materials, manufacturing, transportation and storage in your supply chain.
When you solve a model using the CAM heuristic, the system can determine which facilities should open or close and in what time period. During a solve, a facility can open or close only once. For example, if a facility closes during a solve, it cannot reopen later. Actions such as opening and closing assets or facilities are long-term decisions and should be based on long-term solve horizons. Although the CAM heuristic is flexible enough to accept a wide range of input, you should specify the longest possible time horizon to ensure meaningful results.
To perform a CAM analysis, you must:
-
Enter information in data fields for block nodes in the analysis.
-
Create CAM sets. There must be at least one CAM set available to perform a CAM analysis. You must create CAM sets for these analyses with the Set Tool. A CAM set is a structural set containing Block nodes. Unblocked block nodes that appear as structural sets are not considered as CAM sets.
-
Assign Block nodes to structural sets to create CAM sets. Block nodes represent locations, such as plants and warehouses that can open or close in the analysis. A block node's CAM Set field displays the name of the CAM set to which the node belongs. You can assign each block node to only one structural set. If a block is assigned to more than one set, three dots appear in its CAM Set field. You must remove the block from all but one set.
-
Configure solver options and solve the model. You can configure different solver options for each structural set in a CAM analysis and then solve the model. For each set of facilities, you can specify the:
-
Maximum number of facilities open at the end of the final period
-
Maximum number of facility closures per period
-
Maximum number of facility openings per period
-
Before solving a model, ensure that block nodes in the CAM sets:
-
Are blocked. Unblocked blocks are not considered in a CAM analysis.
-
Display Yes in the Rationalize field. Blocks with No in the Rationalize field are not eligible to be opened or closed in a CAM analysis. You can use this field to exclude Block nodes from CAM analyses. If Block nodes in a CAM set display No in the Rationalize field, this set will not appear in CAM solver options.
Viewing the Results of a CAM Solve
After a CAM solve, you can examine a model to determine what facilities opened or closed in the analysis and how these changes affected production and distribution requirements in each time period.
To view the results of a CAM solve, you can query nodes and arcs in the model. To determine whether facilities opened or closed in the analysis, query the block nodes and view their Open field. Similarly, you can define a report query to display this information in a report. This requires the use of report overrides.
Effect on Sets
In a CAM solve, if a node is in a closed Block and an Under violation occurs, the Under violation (which can occur with Storage and StorageDemand nodes, for example) is not recorded in the Under set. Under violations are only recorded for periods in which the Block is open.
Under, Over, and Backorder violations are recorded on a per period basis.
If a CAM solve closes a Block that contains Demand nodes with existing demand, the demand is assumed to be removed as well. If demand is sourced from a Block that is closed in the solve, the unmet demand is reported in an Under set.
Determining Results Using Report Overrides
You can use report overrides to extract CAM information from your model. Since Block nodes cannot be queried directly using report queries, you must query other nodes in the Block and use report overrides to obtain Block node information. For example, you can use the capmanstatus:n override to determine whether parent Blocks of a node are open or closed in each period.
The following report overrides can be used for extracting CAM information from your model:
| Report Override | Description |
|---|---|
| capmanstatus:n | Extracts the status of the Block node in each period |
| camset:n | Extracts the CAM set of which the Block node is a member. |
| incapmansolve:n | Extracts whether or not the facility is part of the analysis. |
| openatstart:n | Extracts the status (open or closed) of the facility at the start of the solve. |
| shutdownbenefit:n | Extracts the one-time benefit of closing a facility. |
| startupcost:n | Extracts the one-time cost of opening the facility. |
| fixedcost:n | Extracts the fixed cost per period of operating the facility. |
where n specifies the parent Block node n levels higher than the current node.
Tips for Performing CAM Analysis
The following tips can help to ensure the most meaningful results from a CAM analysis
Facilities Can Change States Only Once
The CAM heuristic allows a facility to change states only once. For example, after an opened Block is closed, it cannot be reopened.
Flow and Facility Open Status
A facility's item flow is closely related to its open or close status. When a facility is closed in a period, there is typically no item flow. This includes under or over amounts going in or out of the nodes in the facility in a given period.
However, if the closed facility contains storage-type nodes, inventory activity can still occur in the closed period. This is because initial inject inventory and the storage level in earlier periods can carry over to later periods for consumption. Constraining the storage level to zero in an arbitrary period is thus infeasible.
A separate channel can be modeled to ship excessive inventory, either by another storage location or by having internal demand to take over the ownership of the items. This channel should be modeled outside the rationalized facility.
Create a Stable Period at the End of the Horizon
Consider including in your model a stable period when no facilities change states at the end of the horizon. This is useful for modeling the long-term effects of running the enterprise after all of the rationalization decisions have been made. To model this, set the maximum of openings and closings to 0 in the final months. Doing so creates a stable period at the end of the horizon.
When You Delete a Block Node, its Demand Nodes are also Removed
If a CAM solve closes a Block node that contains Demand nodes, the demand is removed as well. If demand exists that must remain in the model, it should be modeled outside of the Block nodes that are being rationalized. If demand is sourced from a Block that is closed in a solve, the unmet demand is reported in an Under set.
Performance Tuning Parameters
The following optional addroot tags can be used to fine tune CAM performance:
CPX_PARAM_EPGAP. This parameter sets a relative tolerance on the gap between the best integer object and the object of the remaining node. When the value below this value, the Mixed Integer Programming (MIP) optimization is stopped. The syntax is as follows:
CPX_PARAM_EPGAP <mipTolerance>
where mipTolerance can be any value between 0 and 1. The default is 0.1
CPX_PARAM_VARSEL. This parameter sets the rule for selecting the branching variable at the node which has been selected for branching. The syntax is as follows:
CPX_PARAM_VARSEL <mipVarselection>
where mipVarselection can be:
-
-1 Minimum feasibility. This value can result in a quicker first integer feasible solution, but is often slower to reach an optimal integer solution.
-
0 The default value selected by the system.
-
1 Maximum infeasibility. This value forces larger changes earlier, which can result in a quicker overall time to reach the optimal integer solution.
-
2 Pseudo costs, based on pseudo shadow prices.
-
3 Strong branch. This value partially solves several subprograms to determine the best branch.
-
4 Pseudo reduced cost. This value is less intensive than pseudo cost.
CPX_PARAM_MIPEMPHASIS. When an optimal solution is not needed, tweaking the emphasis can help find more feasible solutions which might also speed up the solve time at the expense of proof of optimality. The syntax is as follows:
CPX_PARAM_MIPEMPHASIS <mipEmphasis>
where mipEmphasis can be:
-
0 The default value. This value balances optimality and feasibility.
-
1 This value emphasizes feasibility over optimality.
-
2 This value emphasizes optimality over feasibility.
-
3 This value emphasizes moving the best bound.
-
4 This value emphasizes finding hidden feasible solutions.
CPX_PARAM_MEMORYEMPHASIS. The branch-and-bound algorithm can consume a large amount of memory, depending on the size of your model. This parameter can be used to conserve memory. The syntax is as follows:
CPX_PARAM_MEMORYEMPHASIS <mipConserveMemory>
where mipConserveMemory can be:
-
0 The default value. This value turns off memory conservation.
-
1 This value turns on memory conservation whenever possible.
CPX_PARAM_NODEFILEIND. This parameter allows using node files on disk, even when memory conservation is off.
CPX_PARAM_NODEFILEIND <mipNodeFileInd>
where mipNodeFileInd can be:
-
0 Node files are not used.
-
1 The default value. Node files are created in memory and compressed.
-
2 Node files are created on disk.
-
3 Node files are created on disk and compressed. When memory conservation is on, this is automatically chosen.
Single Sourcing
If you use single sourcing, the whole product mix for a given demand point in a model is sourced from one node. Single sourcing is useful if you require a single contact point with a customer. Single sourcing often happens naturally, without selecting a single sourcing option, because of the cost structure of a model.
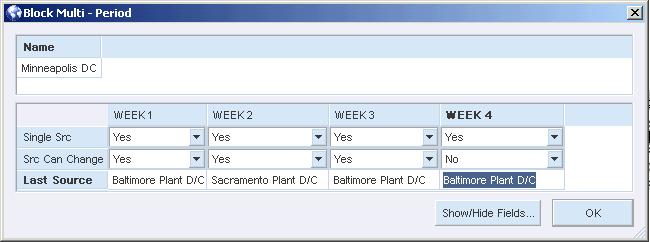
For example, suppose a distribution center in Minneapolis can be supplied by a plant/distribution center in either Sacramento or Baltimore. In the blocked nodes that represent each business location, single sourcing is selected by setting the Single Src field in the Block properties windows to Yes. This action means either Sacramento or Baltimore (not both) is the only source for the entire product mix entering Minneapolis.
The Single Src settings indicate which node sets require single sourcing. The Branch and Bound algorithm can then select optimum sourcing from this information.
In most models, unconstrained linear programming solves tend to be 90 % single-sourced already, with only a small amount of multi-sourced flow. Destinations tend to be single-sourced from the source that "naturally" gives them the highest volume of product.
Example: Single Sourcing
The single sourcing algorithms ensure that the whole product mix entering a block node comes from one source node. In the following example, a distribution center in Minneapolis can be supplied by Sacramento or Baltimore:
You select single sourcing for this node by changing the Single Src fields in a block node query to Yes.
The Src Can Change field is used for multi-period sourcing. If the sourcing in a period has to be identical to the sourcing in the previous period, the Src Can Change field should be set to No. In this example, the sourcing in Week Four must be identical to the sourcing in Week Three.
The Last Source field indicates the name of the source node that was selected in the most recent solve with a single sourcing algorithm.
Single Sourcing Options
The first option is First Periods, in which you specify the number of periods for which single sourcing is done. In many situations, you do not need to make a detailed single sourcing decision for the last periods because the information for business processes in those periods is not present or is not very reliable.
Single Sourcing Algorithm: Round by Volume
Single sourcing algorithms ensure that the whole product mix entering a Block node comes from one source node. The Single Sourcing Algorithm: Round by Volume works as follows:
| Step | Actions |
|---|---|
| Starting Condition | The algorithm uses the optimized linear program from the previous solve phase. |
| Step 1 | Moving forward through periods for First Periods, determine whether any multisourced Block nodes that exist in any period need to change. If so, advance to step 2. If not, advance to step 5. |
| Step 2 | Determine whether all Choices/Resolve changes have been made. If they have, advance to step 4. If they have not, advance to step 3. |
| Step 3 | Find the source that supplies the largest total flow, add constraints that ensure that all commodities are sourced from that node, and then return to step 2. |
| Step 4 | Solve the linear program and return to step 1. |
| Step 5 | The Single Sourcing Algorithm: Round by Volume is complete and the solver advances to the next solve phase. |
Single Sourcing Algorithm: Round by Cost
The Single Sourcing Algorithm: Round by Cost works as follows:
| Step | Actions |
|---|---|
| Starting Condition | The algorithm uses the optimized linear program from the previous solve phase. |
| Step 1 | Moving forward through periods for First Periods, determine whether any multisourced Block nodes that exist in any period need to change. If so, advance to step 2. If not, advance to step 3. |
| Step 2 | Estimate the cost of sourcing using the reduced cost of the source arcs and the total flow of the commodities. Select the source node with the lowest cost estimate and add constraints that ensure that all the commodities are sourced from that node. Store this sourcing in best sourcing and return to step 1. |
| Step 3 | Solve the linear program and advance to step 4. |
| Step 4 | Determine if the next part of the process has been repeated three times. If it has, advance to step 9. If the process has not been repeated three times, advance to step 5. |
| Step 5 | Determine if any more Block nodes need to be changed. |
| Step 6 | Calculate a new estimate for the sourcing costs based on the reduced costs of the source arcs and the total flow of the commodities. Select the source node with the lowest cost estimate and add constraints to ensure that all the commodities are sourced from that node. Return to step 5. |
| Step 7 | Solve the linear program and advance to step 8. |
| Step 8 | Determine whether the cost has gone down, store the new sourcing as best sourcing, and return to step 4. |
| Step 9 | Install the best sourcing, solve the linear program, and advance to step 10. |
| Step 10 | The Single Sourcing Algorithm: Round by Cost is complete and the solver advances to the next solve phase. |
Single Sourcing Algorithm: Branch and Bound
The Branch and Bound algorithm works according to the following recursive scheme:
| Step | Actions |
|---|---|
| Step 1 | The algorithm solves the linear program, and advances to step 2. |
| Step 2 | Determine if the cost from the last solve passes the cost criterion. (See the Cost Criterion topic that follows this table.) If it does, advance to step 3. If it does not, advance to step 6. |
| Step 3 | Moving forward through periods for First Periods, determine if any multisourced Block nodes in any period need to change. If so, advance to step 4. If not, advance to step 5. |
| Step 4 | Select the multi-sourced Block node in a period with the largest total flow. Shut off 50% of the possible sources with the smallest flow, and recursively call Branch and Bound. Turn the 50% back on, and shut off the 50% with the largest flow, and recursively call Branch and Bound. Remove all constraints on this Block node period, and advance to step 6. Note. This step recursively calls Branch and Bound and can take a relatively long time to complete. |
| Step 5 | A new best cost solution has been found. Store the current sourcing as a new best cost sourcing. Store the cost as best cost, and advance to step 6. |
| Step 6 | The Single Sourcing Algorithm: Branch and Bound is complete. |
Cost Criterion
The best cost is initialized with the value in Upper Bound. The cost criterion depends on the settings for the Branch and Bound algorithm on the Single Sourcing Options window. The following table describes the options:
| Option | Cost Criterion |
|---|---|
| Full solve | cost < best cost |
| Skip branch if less than n percent improvement | cost < (100-n)% of best cost |
| Skip branch if less than n cost improvement | cost < (best cost -n) |
More About Branch and Bound
Branch and Bound is a recursive algorithm that finds the optimum (least cost) solution for a feasible problem, given enough time. It has a decision process for selecting which variables are involved in a node and which ones should be shut off.
For each decision node, the set of sources (for example, either Sacramento or Baltimore) for a destination (Minneapolis) that are currently not shut off are chosen and summed to the highest volume of flow. These results become the node's decision variables. The sources are then sorted in decreasing order of volume.
The solution is represented by a tree with two possible paths, which are represented by the branches extending from the decision node. Each level down the tree has twice as many possible solutions as the previous level.
The Branch and Bound algorithm travels down the tree until it finds the best solution by making sourcing decisions at each vertex. On the left branch, if shuts off the lowest volume sources. On the right branch, it shuts off the highest volume sources. It always takes the left branch first, and it follows a depth-first search. These are resource-driven selection rules. Experimentation shows that this technique works best for sourcing problems.
The net effect is that the Branch and Bound solver initially follows a path that assigns all of the destinations to their highest volume source (just like the Round by Volume heuristic). The advantage is that it helps the Branch and Bound solver get a feasible solution as quickly as possible. When Branch and Bound first starts, it assumes an infinite bound until it gets a feasible solution that satisfies all of the 0-1 constraints.
This volume-driven first solution is often very close to the optimum solution. The closer the bound is to the optimum, the sooner the Branch and Bound algorithm can prune bad solutions in the tree, and the sooner it can return the answer.
Limiter Algorithms
If you select the Limiter option, the solver determines what commodities to use based on the values in the Max Outputs field of the Limiter nodes. A Limiter node limits the total number of commodities that can flow through it, thereby constraining the number of products that are produced in a time period. If you do not select the Limiter heuristics, the system ignores the constraints. In the Limiter Options window, the First Periods field shows the number of periods, starting at the first period, for which the Limiter constraints are enforced.
Limiter Algorithm: Round Down Move Backward
The Limiter Algorithm: Round Down Move Backward works as follows:
| Step | Actions |
|---|---|
| Starting Condition | The algorithm uses the optimized linear program from the previous solve phase. |
| Step 1 | Determine if the algorithm is finished going through periods in reverse order for First Periods. If it is not finished, advance to step 2. If it is finished, advance to step 5. |
| Step 2 | Determine if any Limiter nodes remain to be processed in the period. If so, advance to step 3. If not, return to step 1. |
| Step 3 | For the current period, find the Limiter node with the largest flow that violates its Limiter constraints. If only n commodities are allowed to flow through the node, then keep then commodities with the largest flows, and shut off all other commodities. Advance to step 4. |
| Step 4 | Resolve the linear program one time every Choices/Resolve time. Return to step 2. |
| Step 5 | Determine if a final linear programming solve is required. If so, solve and advance to step 6. If not required, advance to step 6 without solving. |
| Step 6 | The Limiter Algorithm: Round Down Move Backward is complete and the solver advances to the next solve phase. |
Limiter Algorithm: Dual Descent
The Limiter Algorithm: Dual Descent works as follows:
| Step | Actions |
|---|---|
| Starting Condition Step 1 Step 2 Step 3 | The algorithm uses the optimized linear program from the previous solve phase. |
| Step 1 | Shut off all commodities for all Limiter nodes in all periods and advance to step 2. |
| Step 2 | Solve the linear program and advance to step 3. |
| Step 3 | Moving forward through periods for First Periods, search for a commodity that can be added to a Limiter node in any period based on the reduced costs in the solution. If a commodity can be added, advance to step 4. If no commodity can be added, advance to step 5. |
| Step 4 | Enable the flow of the commodity in the Limiter node for that period. Return to step 2. |
| Step 5 | The Limiter Algorithm: Dual Descent is complete and the solver advances to the next solve phase. |
Minimum Run Length
The Minimum Run Length option directs the solver to respect the minimum run length (in amount of flow) when solving your model. You can specify the minimum run length constraint in a batch node. The flow through the node must be zero or must be greater than or equal to the minimum run length.
The batch node can also model setup times at the start of a period. When a setup must be done, the batch node pulls time from the machine connected to the top attach point of the batch node. Time is just a commodity and has nothing to do with how the periods are structured.
The use of setup times can be modeled in two ways:
-
In every period where there is a run, create Setup demand on the top attach point of the batch node (Single Period Setups is Yes)
-
Create Setup demand on the top attach point of the batch node (Single Period Setups is No) only in the first period of a range of runs
Minimum Run Length Options
The First Periods field in the Minimum Run Length Options dialog shows the number of periods for which the Minimum Run Length constraints are enforced. Two initial algorithms exist for Minimum Run Length: Round Down Move Backward and Dual Descent (normal and violations only).
Minimum Run Length Algorithm: Round Down Move Backward
The Minimum Run Length Algorithm: Round Down Move Backward works as follows:
| Step | Actions |
|---|---|
| Starting Condition | The algorithm uses the optimized linear program from the previous solve phase. |
| Step 1 | Determine if the algorithm is finished going through periods in reverse order for First Periods. If it is finished, advance to step 7. If it is not finished, advance to step 2. |
| Step 2 | Determine if any Batch nodes violate their minimum run length. If so, advance to step 3. If not, advance to step 5. |
| Step 3 | For the current period, find the Batch node with the largest violation of its minimum run length. Shut off the flow through this node, and handle the change in Setup where needed. Advance to step 4. |
| Step 4 | Once every Choices/Resolve time, resolve the linear program. Return to step 2. |
| Step 5 | Create constraints that ensure that the flow through the active Batch nodes in this period remains larger than their minimum run lengths. Advance to step 6. |
| Step 6 | Resolve the linear program and return to step 1. |
| Step 7 | If Tune is selected, enter Tune phase. If not, advance to step 8. |
| Step 8 | The Minimum Run Length Algorithm: Round Down Move Backward is complete and the solver advances to the next solve phase. |
Minimum Run Length Algorithm: Dual Descent (Normal)
The Minimum Run Length Algorithm: Dual Descent (Normal) works as follows:
| Step | Actions |
|---|---|
| Starting Condition | The algorithm uses the optimized linear program from the previous solve phase. |
| Step 1 | Shut off all the flows for all Batch nodes in all periods for First Periods, and advance to step 2. |
| Step 2 | Solve the linear program and advance to step 3. |
| Step 3 | Search for a commodity that can be added to a Batch node in a period based on the reduced costs in the solution. If a commodity can be added, advance to step 4. If no commodity can be added, advance to step 5. |
| Step 4 | Enable the flow of the Batch node in the period. Ensure that the flow is greater than or equal to the minimum run length and handle the change in Setup if needed. Return to step 2. |
| Step 5 | If Tune is selected, enter Tune phase. If not advance to step 6. |
| Step 6 | The Minimum Run Length Algorithm: Dual Descent (Normal) is complete, and the solver advances to the next solve phase. |
Minimum Run Length Algorithm: Dual Descent (Violations Only)
The Minimum Run Length Algorithm: Dual Descent (Violations Only) algorithm works as follows:
| Step | Actions |
|---|---|
| Starting Condition | The algorithm uses the optimized linear program from the previous solve phase. |
| Step 1 | Moving forward in time for First Periods, determine if all Batch nodes in all periods have been analyzed. If so, advance to step 3. If all Batch nodes in all periods have not been analyzed, advance to step 2. |
| Step 2 | If the flow in the Batch node is set to its minimum run length, set its lower bound to that minimum run length. Otherwise, shut off the flow by setting the upper bound to zero. Handle the change in Setup where needed and advance to step 3. |
| Step 3 | Solve the linear program and advance to step 4. |
| Step 4 | Search for a commodity that can be added to a Batch node in a period based on the reduced cost in the solution. If a commodity can be added, advance to step 5. If no commodity can be added, advance to step 6. |
| Step 5 | Enable the flow of the Batch node by setting the upper bound to infinity and the lower bound to the minimum run length. Handle the change in Setup where needed, and return to step 3. |
| Step 6 | If Tune is selected, enter Tune phase. If not, advance to step 7. |
| Step 7 | The Minimum Run Length Algorithm: Dual Descent (Violations Only) is complete, and the solver advances to the next solve phase. |
Minimum Run Length Algorithm: Tune
The Minimum Run Length Algorithm: Tune algorithm works as follows:
| Step | Actions |
|---|---|
| Starting Condition | The algorithm uses the Minimum Run Length feasible linear program from the previous Minimum Run Length algorithm. |
| Step 1 | Determine if a run can be added to a Batch node in any period, based on the reduced cost in the solution. If a run can be added, advance to step 2. If a run cannot be added, or if the reduced cost is less than the Stop Cost, or if the (number of) Tries has been exceeded, advance to step 6. |
| Step 2 | Enable the run by setting the upper bound to infinity and the lower bound to the minimum run length. Handle the change in Setup where needed and advance to step 3. |
| Step 3 | Solve the linear program and advance to step 4. |
| Step 4 | Determine whether the new cost is higher than the previous cost. If so, advance to step 5. If not, return to step 1. |
| Step 5 | Undo the changes that were made in step 2, and return to step 1. |
| Step 6 | Determine if a run can be removed from a Batch node in any period, based on the reduced cost in the solution. If a run can be removed, advance to step 7. If a run cannot be removed, or if the reduced cost is less than the Stop Cost, or if the (number of) Tries has been exceeded, advance to step 11. |
| Step 7 | Remove the run by changing the upper and lower bounds to zero, and handle the change in Setup where needed. Advance to step 8. |
| Step 8 | Solve the linear program and advance to step 9. |
| Step 9 | Determine if the new cost is higher than the previous cost. If so, advance to step 10. If not, return to step 6. |
| Step 10 | Undo the changes that were made in step 7, and return to step 6. |
| Step 11 | Determine if any run can be moved to a different period for a Batch node in any period, based on the reduced cost in the solution. If a run can be moved to a different period, advance to step 12. If a run cannot be moved to a different period, or if the reduced cost is less than the Stop Cost, or if the (number of) Tries has been exceeded, advance to step 16. |
| Step 12 | Move the run by changing the upper and lower bounds of the flow in those periods, and handle the change in Setup where needed. Advance to step 13. |
| Step 13 | Solve the linear program and advance to step 14. |
| Step 14 | Determine if the new cost is higher than the previous cost. If so, advance to step 15. If not, return to step 11. |
| Step 15 | Undo the changes that were made in step 12, and return to step 11. |
| Step 16 | The Minimum Run Length Algorithm: Tune is complete and the solver advances to the next solve phase. |
Note: Minimum Run Length Algorithm: Tune uses the following parameters as stopping criteria:
-
Stop Cost. Consider making changes only if the reduced cost of adding, removing, or moving a run is greater than the Stop Cost value.
-
Tries. Stop the Tune algorithm after trying for a certain number of times to improve the solution.
The Batch Heuristic
The Batch heuristic is used to ensure that batch size requirements are respected. The size of a batch, in amount of flow, is specified in the Batch nodes.
The First Periods field shows the number of periods for which the batch size constraints are enforced. The Batch algorithm is very similar to the Round Down Move Backward algorithm for Minimum Run Length. You can select scripts to run after each batch sequence. Only Strategic Network Optimization Batch commands can be run.
Note: New objects added by a batch script are not considered when the model is solved.
To set this option:
-
Select Configure from the Solve menu.
-
Click the Options button in the Batch area.
-
In the Batch Options window, click the Advanced button.
-
In the Batch Scripts window, click the Add button and add scripts.
-
Click OK.
Batch Algorithm: Tune
The Batch Algorithm: Tune works as follows:
| Step | Actions |
|---|---|
| Starting Condition | The algorithm uses the Batch feasible linear program from the previous Batch algorithm. |
| Step 1 | Determine if a batch can be added to a Batch node in any period, based on the reduced cost in the solution. If a batch can be added, advance to step 2. If a batch cannot be added, or if the reduced cost is less than the Stop Cost, or if the (number of) Tries has been exceeded, advance to step 6. |
| Step 2 | Fix the flow at the new level, and advance to step 3. |
| Step 3 | Solve the linear program and advance to step 4. |
| Step 4 | Determine whether the new cost is higher than the previous cost. If so, advance to step 5. If not higher, return to step 1. |
| Step 5 | Undo the changes that were made in step 2, and return to step 1. |
| Step 6 | Determine if a batch can be removed from a Batch node in any period, based on the reduced cost in the solution. If a batch can be removed, advance to step 7. If a batch cannot be removed, or if the reduced cost is less than the Stop Cost, or if the (number of) Tries has been exceeded, advance to step 11. |
| Step 7 | Fix the flow at the new level and advance to step 8. |
| Step 8 | Solve the linear program and advance to step 9. |
| Step 9 | Determine if the new cost is higher than the previous cost. If so, advance to step 10. If not, return to step 6. |
| Step 10 | Undo the changes that were made in step 7, and return to step 6. |
| Step 11 | Determine if a batch can be moved to a later period for a Batch node in any period, based on the reduced cost in the solution. If a batch can be moved to a later period, advance to step 12. If a batch cannot be moved to a later period, or if the reduced cost is less than the Stop Cost, or if the (number of) Tries has been exceeded, advance to step 16. |
| Step 12 | Fix the flow in the two periods at the new level, and advance to step 13. |
| Step 13 | Solve the linear program and advance to step 14. |
| Step 14 | Determine whether the new cost is higher than the previous cost. If not, return to step 11. If so, advance to step 15. |
| Step 15 | Undo the changes that were made in step 12, and return to step 11. |
| Step 16 | The Batch Algorithm: Tune is complete and the solver advances to the next solve phase. |
Note: Batch Algorithm: Tune uses the following parameters as stopping criteria:
-
Stop Cost. Consider making changes only if the reduced cost of adding, removing, or moving a run is greater than the Stop Cost value.
-
Tries. Stop the Tune algorithm after trying for a certain number of times to improve the solution.
Batch Algorithm: Round Down Move Backward
The Batch Algorithm with Round Down Move Backward works as follows:
| Step | Actions |
|---|---|
| Starting Condition | The algorithm uses the optimized linear program from the previous solve phase. |
| Step 1 | Determine if the algorithm is finished going through periods in reverse order for First Periods. If it is finished, advance to step 6. If it is not finished, advance to step 2. |
| Step 2 | Collect batch information and order the nodes first according to Sequence and then by the highest Production Batch ratio. Production Batch ratio is calculated by flow divided by batch size. This number does not need to be an integer. For example, if the flow is 100 and the batch is 30, the Production Batch ratio is 3.33333. Determine if all Batch nodes have been fixed at a multiple of their batch size. If they have all been fixed, advance to step 5. If they have not all been fixed, advance to step 3. |
| Step 3 | For the current period, find the Batch node with the largest batch violation. Fix the flow through this node at the nearest batch multiple under its current flow value. Advance to step 4. |
| Step 4 | Resolve once every Choices/Resolve time or when the current Sequence number is different than the previous Sequence number. Return to step 2. |
| Step 5 | Solve the linear program and return to step 1. |
| Step 6 | If Tune is selected, enter Tune phase. If not advance to step 7. |
| Step 7 | The Batch algorithm is complete and the solver advances to the next solve phase. |
First Periods is set in the Batch Options window which can be accessed by selecting Solve, then Configure from the main menu, and then clicking the Options button for Batch. Sequence is set in node properties windows.
Load Smoothing
In some processes, keeping the production level identical to the level in the previous period is desirable, if the changes in the production level are relatively small. With Load Smoothing, you can model this by setting a Change Threshold that ensures that the flow in two consecutive periods of a MachineDelta node is identical or is greater than the Change Threshold value.
If Load Smoothing is turned on, the system respects the Change Threshold. If Load Smoothing is turned off, this Change Threshold is ignored.
In addition, a Change Cost is charged if the flow amount changes from one period to the next. The Change Cost is charged even if the Load Smoothing algorithm is not selected for a solve. Similarly, the Max Up Change and Max Down Change fields of the MachineDelta node are considered, regardless of the Load Smoothing Algorithm.
The Load Smoothing algorithm works as follows:
| Step | Actions |
|---|---|
| Starting Condition | The algorithm uses the optimized linear program from the previous solve phase. |
| Step 1 | Moving forward through periods, determine if more MachineDelta nodes remain in any period to change. If so, advance to step 2. If not, advance to step 5. |
| Step 2 | For a MachineDelta node in a period, determine if the flow in this period has changed less than the threshold. If it has changed less than the threshold, advance to step 3. If it has not, advance to step 4. |
| Step 3 | Change the values of the Max Up Change and Max Down Change constraints to zero, remove the Change Cost for this node and period, and advance to step 4. |
| Step 4 | Solve the linear program and return to step 1. |
| Step 5 | The Load Smoothing algorithm is complete and the solver advances to the next solve phase. |
To enable Load Smoothing:
-
From the Solve menu, select Configure.
-
In the Load Smoothing drop-down list, select On.
Note: The Load Smoothing heuristic only affects MachineDelta nodes that have production capacities limited by Change Thresholds.
The Effects of Heuristics
If your model uses heuristics, you must use extra care when solving only part of it. If areas of a model close to the nodes that are used in the heuristic solve are fixed, an infeasible solve is likely.
| Heuristic | Restricted Solve Issues |
|---|---|
| CAM | Because this heuristic is used for strategic business analysis and the algorithm makes decisions on the global configuration of the enterprise, restricted solves do not work with it. |
| Limiter | If the Limiter node is part of the set to be re-solved, the flows it is limiting should also be part of the re-solve. |
| Load Smoothing | Ensure that the area of the model surrounding the Machine Delta node is part of the restricted solve. |
| Minimum Run Length and Batch | If the Batch node is part of the model being re-solved, ensure that the flow to and from the Batch node has enough freedom to get a feasible Batch solve. |
| Single Sourcing | Ensure that the single sourcing Block node is in the set of elements to be re-solved and that all the sources of the node are part of the re-solve. |