The two basic inventory decisions that managers face are:
Although it is possible to consider these two decisions separately, they are so closely related that a simultaneous solution is usually necessary. Typically, the objective is to minimize total inventory costs. Total inventory costs typically include holding, ordering, shortage, and purchasing costs.
In a continuous review system, managers continuously monitor the inventory position. Whenever the inventory position falls at or below a level R, called the reorder point, the manager orders Q units, called the order quantity. (Note that the reorder decision is based on the inventory position including orders and not the inventory level. If managers used the inventory level, they would place orders continuously as the inventory level fell below R until they received the order.) When you receive the order after the lead-time, the inventory level jumps from zero to Q, and the cycle repeats.
In inventory systems, demand is usually uncertain, and the lead-time can also vary. To avoid shortages, managers often maintain a safety stock. In such situations, it is not clear what order quantities and reorder points will minimize expected total inventory cost. Simulation models can address this question.
In this example, demand is uncertain and is Poisson distributed with a mean of 100 units per week. Thus, the expected annual demand is 5,200 units.
For large values of the rate parameter, |
Additional relationships that hold for the inventory system are:
Each order costs $50 and the holding cost is $0.20 per unit per week ($10.40 for one year).
Every unfilled demand is lost and costs the firm $100 in lost profit.
The time between placing an order and receiving the order is 2 weeks. Therefore, the expected demand during lead-time is 200 units. Orders are placed at the end of the week, and received at the beginning of the week.
The traditional economic order quantity (EOQ) model suggests an order quantity:
For the EOQ policy, the reorder point should equal the lead-time demand; that is, place an order when the inventory position falls to 200 units. If the lead-time demand is exactly 200 units, the order will arrive when the inventory level reaches zero.
However, if demand fluctuates about a mean of 200 units, shortages will occur approximately half the time. Because of the high shortage costs, the manager would use either a larger reorder point, a larger order quantity, or both. In either case, the manager will carry more inventory on average, which will result in a lower total shortage cost but a higher total holding cost. A higher order quantity lets the manager order less frequently, thus incurring lower total ordering costs. However, the appropriate choice is not clear. Simulation can test various reorder point/order quantity policies.
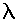 , the Poisson distribution is approximately normal. Thus, this assumption is tantamount to saying that the demand is normally distributed with a mean of 100 and standard deviation of
, the Poisson distribution is approximately normal. Thus, this assumption is tantamount to saying that the demand is normally distributed with a mean of 100 and standard deviation of 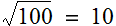 . The Poisson distribution is discrete, thus eliminating the need to round off normally distributed random variates
. The Poisson distribution is discrete, thus eliminating the need to round off normally distributed random variates