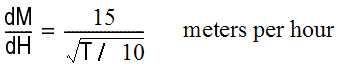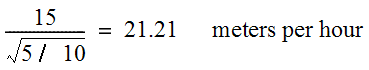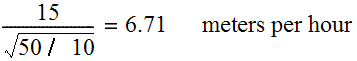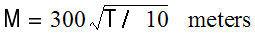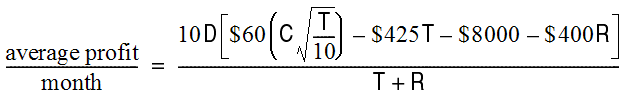When drilling wells in certain types of terrain, the performance of a drill bit erodes with time because of wear. After T hours, the drilling rate can be expressed as:
For example, after 5 hours of consecutive use (starting with a new drill bit), the drill is able to penetrate the terrain at a rate of:
While after 50 hours, the penetration rate is only:
Eventually, the bit must be replaced as the costs exceed the value of the well being drilled. The problem is to determine the optimum replacement policy; that is, the drilling cycle, T hours, between replacements.
T hours after replacing the bit, the total drilled depth in meters, M, is given by the integral of Equation 4.2 from 0 to T, or:
where 300 is a drilling depth coefficient.
The revenue value per meter drilled is calculated to be $60. Drilling expenses are fixed at $425 per hour, and it generally requires R = 7.5 hours to install a new drill bit, at a cost of $8,000 + $400R.
If all drilling parameters were certain, calculating the optimal replacement policy would be straightforward. However, several of the drilling parameters are uncertain, and knowledge about their values must be assumed:
Because of variations in the drilling process and terrain, the depth coefficient, C, is characterized by a normal distribution with a mean of 300 and a standard deviation of 20.
The drill bit replacement time, R, varies and is determined by a triangular distribution with parameters 6.5, 7.5, and 9.
The number of 10-hour days available per month, D, also varies due to the weather and the number of days in a month, and is assumed to be triangular with parameters 24, 28, and 30.
With these assumptions, the profit/drilling cycle if the bit is replaced after T hours equals the revenue obtained from drilling minus drilling expenses and replacement costs:
profit/drilling cycle = $60M - $425T - ($8,000 + $400R)
Assuming D ten-hour days per month, the average number of cycles per month is 10D/(T + R). Therefore, the average profit per month is:
The objective is to find the value of T that maximizes the average profit per month.