This case is also known as regression through origin.
The regression equation without constant is
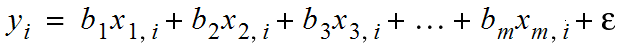
This can be written in matrix format as Y = bX + ∊, where Y and b are column vectors of dimension n by 1 and X is a matrix of the dimension n by m, where n is the number of observations and m is the number of independent variables. It is assumed that n > m.
Here, too, Predictor uses singular value decomposition (SVD) to determine b, the coefficients of the regression equation. The only difference between this case and regression with a constant is the dimension of the matrices.
For related regression statistics, see Statistics, Standard Regression without Constant.