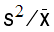Suppose a particular mechanical system fails after receiving exactly 5 shocks to it from an external source. The total time to system failure, defined as the random time occurrence of the 5th shock, follows a gamma distribution with a shape parameter of 5.
Some characteristics of the gamma distribution:
When shape = 1, gamma becomes a scalable exponential distribution.
The sum of any two gamma-distributed variables is a gamma variable.
If you have historical data that you believe fits the conditions of a gamma distribution, computing the parameters of the distribution is easy. First, compute the mean and variance of the historical data:
Parameter Symbol mean =
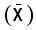
variance =
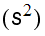
Then compute the distribution’s parameters:
Parameter Symbol shape =
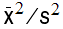
scale =