The term "Moving" when used with functions such as Moving Averages usually refers to a fixed window or "sub-range" of analysis that moves over a larger range of numeric data values. For each window, a calculation such as an average (mean) is performed. As the window moves over the larger range, one number value is dropped from the window and a new value is added.
To illustrate the effect of Moving Averages as opposed to a simple average (mean) consider the following list of arbitrary "Sales" values over a period of twelve months as shown in a Table or Results section:
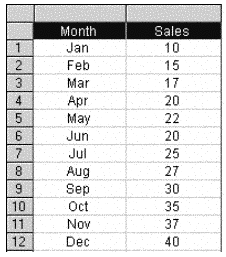
The simple mean value of all of the above twelve Sales values is:
Sum of all twelve values divided by 12 = 296 / 12 = 24.67
While having some virtue, this simple mean value does not offer any insight into analyzing the variation trend of the original values or to provide a more accurate mean value at varying points of the range. Moving Averages, on the other hand, do offer the ability to understand the trend of data by calculating many average (mean) values over the entire range of original data values.
There are several variations to Moving Average calculation, the most common of these are: Simple Moving Averages, Weighted Moving Averages and Exponential Moving Averages. All of these variations are described in detail in the following sections. Additionally, other "Moving Functions": Moving Maximum, Moving Minimum, Moving Median, Moving Sum and Moving Difference whose functionality closely resembles that of Moving Averages are discussed.