Exponential Moving Averages, similar to Weighted Moving Averages, also assign a greater weight to more recent data values. Unlike Weighted Moving Averages, however, they use the previously calculated Exponential Moving Average value as a basis for calculation rather than the original (non-Averaged) data values. In this way, the calculation method used by Exponential Moving Averages is cumulative, meaning that (unlike Simple Moving Averages or Weighted Moving Averages) all previous data values have some effect on the Exponential Moving Average to be calculated, although this effect diminishes greatly with time.
Exponential Moving Averages tend to be more accurate than the other types of Moving Average when the original data values show a more rapid degree of variation over time (or other variable).
The formula for calculating an Exponential Moving Average (EMA) is:
X = (K * (C - P)) + P
X = Current EMA (i.e. EMA to be calculated)
C = Current original data value
(The first EMA in the range to be calculated is arbitrary and can be the corresponding original data value or, often, a Simple Moving Average value.
K = Smoothing Constant = 2 / (1 + n)
n = number of periods for EMA i.e. the Window to calculate.
This rather complex calculation is, perhaps, best illustrated by example.
Consider the table of monthly Sales values as shown previously:
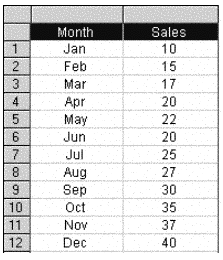
If we calculated the Exponential Moving Average in a similar fashion to the 3-Month Simple Moving Average, we would perform the following steps:
 To calculate the exponential moving average:
To calculate the exponential moving average:
Calculate the Smoothing Constant according to the 2 / (1 + n) formula.
N = window of values = 3, therefore the Smoothing Constant is:
2 / (1 + 3) = 0.5
For the first Exponential Moving Average, use the first original data value (in this case, that for the Month of "Jan").
For subsequent values, follow the calculation according to the above formula.