对于 Portfolio Revisited.xlsx 中描述的资产,如果研究一下所有可能的投资战略组合,您会发现,每个组合都有特定的平均回报以及与其关联的回报标准偏差。在一个轴上绘制平均值,在另一个轴上绘制标准偏差,创建的图形类似于:
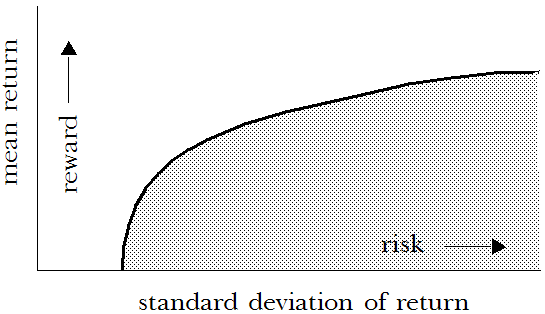
在曲线上或曲线下方的点(低于曲线的值)表示可能的投资组合。曲线上方的点(高于曲线的值)表示在给定特定资产的情况下无法得到的组合。对于给定的任何平均回报,一个组合具有可能的最小标准偏差。该组合在曲线与平均回报交叉的点上。
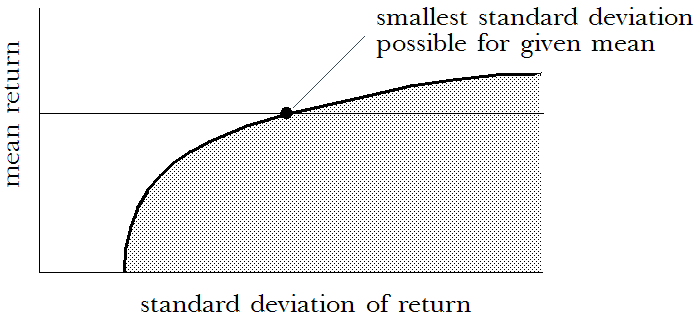
同样,对于给定的任何回报标准偏差,一个组合有可实现的最高平均回报。该组合在曲线与回报标准偏差交叉的点上。
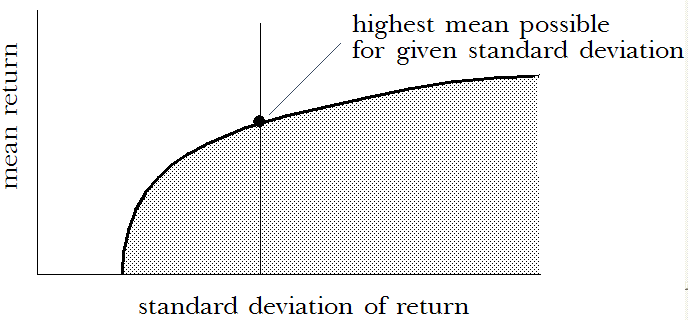
直接在曲线上的组合称为“有效组合”(请参阅《Oracle Crystal Ball Reference and Examples Guide》中 OptQuest 部分的公共参考资料中列出的 Markowitz 于 1991 年发布的理论),因为在不生成更高标准偏差的情况下不可能获得更高的平均回报,在不生成更低平均回报的情况下也不可能获得更低的标准偏差。有效组合的曲线通常称为“有效边界”。
值低于曲线的组合称为“无效组合”,表示存在更好的组合:回报更高和/或标准偏差更低。
“教程 2 - Portfolio Allocation 模型”中的示例使用了一个技巧在有效边界上搜索最优解决方案。这种方法使用回报的平均值和标准偏差作为平衡风险与报酬的标准。
您也可以使用其他选择组合的标准。您可以选择中位数或众数作为集中趋势的度量,而不使用平均回报。这些选择标准称为“有效中位数-标准偏差”或“有效众数-标准偏差”。您可以选择方差、范围下限或百分点下限作为风险或不确定性的度量,而不使用回报标准偏差。这些选择标准称为“有效平均值-方差”、“有效平均值-范围下限”或“有效平均值-百分点”。