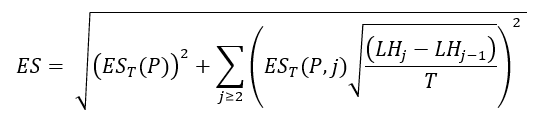
This section includes the details of the following back-end computations.
Topics:
· Historical Simulation - Output Metrics
· Model Validation - PLA Attribution Tests
The outputs are:
· ES and VaR:
This option calculates the Expected Shortfall (ES) and Value at Risk (VaR) using the current observation period.
VaR is computed as the maximum amount of potential loss that can occur for given confidence and time horizon.
ES is computed using the following equation:
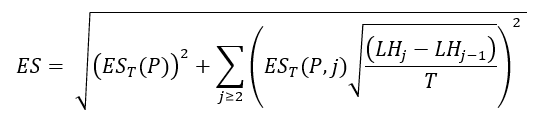
Where,
ES is the regulatory liquidity-adjusted expected shortfall
T is the length of the base horizon
 is the expected shortfall
at horizon T of a portfolio P
is the expected shortfall
at horizon T of a portfolio P
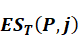 is the expected shortfall
at horizon T of a portfolio P with respect to shocks for the subset of
risk factors Q (j), with all other risk factors held constant
is the expected shortfall
at horizon T of a portfolio P with respect to shocks for the subset of
risk factors Q (j), with all other risk factors held constant
Q (j) is the subset of risk factors whose liquidity
horizon is at least as long as 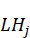
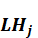 is the
liquidity horizon j as specified by in the Liquidity Horizon user interface
is the
liquidity horizon j as specified by in the Liquidity Horizon user interface
· Stress Calibrated for ES:
This selection provides you the option to specify the stress window
If you choose to define the observation period, toggle the Identified Period button and provide the Observation Start Date and Observation End Date.
Stress calibrated ES is computed using the following equation:
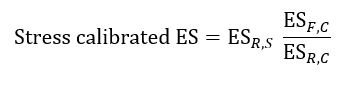
Where,
 is Expected shortfall
for reduced set of risk factor and stress observation period
is Expected shortfall
for reduced set of risk factor and stress observation period
i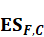 s
Expected shortfall for the full set of risk factor and current observation
period
s
Expected shortfall for the full set of risk factor and current observation
period
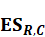 is Expected shortfall
for reduced set of risk factor and current observation period
is Expected shortfall
for reduced set of risk factor and current observation period
For Reduced set, ES Metrix calculation (ES(R, C)), a reduced set Validation Result must have Valid status.
· Internally Modelled Capital Charge:
If you select this option, specify the relative weight assigned to the firm’s internal model. This output is required to compute Internally Modelled Capital Charge (IMCC).
IMCC is computed using the following equation:
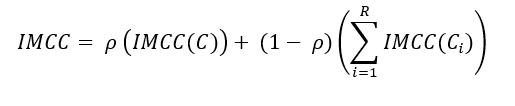
Where,
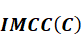 is Stress calibrated ES
is Stress calibrated ES
 is stress calibrated
ES with respect to shocks for broad risk factors class i with all
other risk factors held constant
is stress calibrated
ES with respect to shocks for broad risk factors class i with all
other risk factors held constant
i is broad regulatory risk classes: interest rate risk, equity risk, foreign exchange risk, commodity risk, and credit spread risk
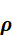 is
the relative weight assigned to the firm’s internal model
is
the relative weight assigned to the firm’s internal model
· Stress Capital Add-on Charge:
Select this option to set the computation of stress scenario capital charge (SES) with execution.
Stress capital add-on is computed using the following equation:
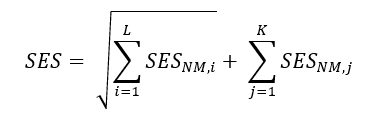
Where,
L is a non-modellable idiosyncratic risk factor
K is non-modellable non idiosyncratic risk factor
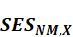 is
the stress scenario capital charge for non-modellable risk factor X, with
respect to shock for X risk factor with all other risk factors held constant
is
the stress scenario capital charge for non-modellable risk factor X, with
respect to shock for X risk factor with all other risk factors held constant
· Aggregated Charge:
Select this option to set the computation of Aggregated Charge with execution. Computation of aggregated charge requires a multiplier. A multiplier is the number that is associated with the number of exceptions arrived in Model Validation. Select the business definition defined in the Model Validation module from the drop-down list, to add a multiplier. If not selected, the system will take 1.5 as the default value of the multiplier.
Aggregated Charge is computed using the following equation:
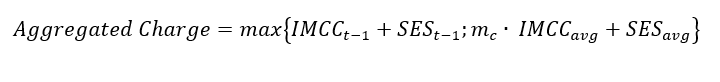
Where,
IMCC and SES average is the average taken over 60-days
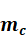 is
multiplier derived from the backtesting model.
is
multiplier derived from the backtesting model.
The PLA requirements are based on two test metrics:
· The Spearman correlation metric to assess the correlation between Risk-Theoretical P&L (RTPL) and Hypothetical P&L (HPL).
· The Kolmogorov-Smirnov (KS) test metric to assess the similarity of the distributions of RTPL and HPL.
To calculate each test metric for a trading desk, the time series of the recent 250 trading days of observations of RTPL and HPL are used.
· For HPL, banks or financial institutions must produce a corresponding time series of ranks based on the size of the P&L (𝑅HPL). That is, the lowest value in the HPL time series receives a rank of 1, the next lowest value receives a rank of 2, and so on.
· For RTPL, banks/financial institutions must produce a corresponding time series of ranks based on size (𝑅RTPL).
Banks calculate the Spearman correlation coefficient of the two-time series of rank values of 𝑅RTPL and 𝑅HPL based on size using the following formula:
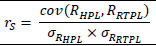
Where,
𝜎𝑅HPL and 𝜎𝑅RTPL are the standard deviations of 𝑅RTPL and 𝑅HPL.
The bank must calculate the empirical cumulative distribution function of RTPL. For any value of RTPL, the empirical cumulative distribution is of 0.004observations that are less t to the specified RTPL.
The bank must calculate the empirical cumulative distribution function of HPL. For any value of HPL, the empirical cumulative distribution is the product of 0.004 and the number of HPL observations that are less than or equal to the specified HPL.
The tric is the largest absolute difference observed between these two empirical cumulative distribution functions at any P&L value.
Based on the outcome of the metrics, a trading desk is allocated to a PLA test red zone, an amber zone, or a green zone as mentioned in the following table.
· A trading desk is in the PLA test green zone if both
§ the correlation metric is above 0.80; and
§ the KS distributional test metric is below 0.09 (p-value = 0.264).
· A trading desk is in the PLA test red zone if the correlation metric is less than 0.7 or if the KS distributional test metric is above 0.12 (p-value = 0.055).
· A trading desk is in the PLA amber zone if it is allocated neither to the green zone nor to the red zone.
Zone |
Spearman Correlation |
KS Test |
|---|---|---|
Amber Zone Thresholds |
0.80 |
0.09 (p-value = 0.264) |
Red Zone Thresholds |
0.70 |
0.12 (p-value = 0.055) |