12    Monte Carlo Analytics

This chapter describes the details of stochastic processing used within Oracle Asset Liability Management (ALM) and Funds Transfer Pricing (FTP). This includes the detailed architecture of the Monte Carlo rate generator that is used for stochastic forecasts of interest rates and calculation of market value, Value-at-Risk, and Earnings-at-Risk.

Topics:

·        Overview 

·        Architecture of the Rate Generator 

·        Arbitrage Term Structure Model 

·        No-Arbitrage Term Structure Models 

·        Yield Curve Smoothing 

·        Calibration 

·        Random Number Generation 

·        Rate Conversion 

·        Output From Monte Carlo 

·        Value-at-Risk 

·        Varying the At-Risk Period 

·        Earnings-at-Risk 

·        Recommended Configuration 

·        Term Structure Models 

·        Term Structure Parameters Format 

·        Choosing a Smoothing Method 

·        Defining a Rate Index Formula 

·        References 

Overview

Monte Carlo is a valuation technique that provides a direct and robust simulation of interest rate paths and provides for market value and Value-at-Risk (VaR) calculations. Monte Carlo becomes a necessary tool in financial markets for solving problems when other methods are unavailable for problems in high dimensions, simulation, and optimization. For Oracle Asset Liability Management (ALM) and Funds Transfer Pricing (FTP) processes, Monte Carlo is a particularly useful tool for valuing instruments with uncertain cash flows. Examples of such instruments include:

·        Callable debt

·        Capped loans

·        Prepayable mortgages

The Monte Carlo rate generator is a calculation engine that forecasts future rate changes within a stochastic process. Central to the understanding of the rate generator is the acknowledgment that a rate forecast will always be imperfect. This means that future rates will not fully match the prognosis given by the model. However, it is possible to quantify the uncertainty of future interest rates or, in other terms, to forecast a probability distribution of interest rates.

Economic theory tells us that there are two types of forecasts:

·        forecast of the real interest rates, based on a “subjective” assessment of the economy

·        forecast of the risk-neutral interest rates, based on the original yield curve and the no-arbitrage condition.

The two types of prognosis will not necessarily match. A bank would typically use the first type of rate to model future income because it wants its income forecast to be as close as possible to the actual future income. A bank would typically use the second type of rate to calculate present and future market value because market value depends not only on the rates but also on the degree of risk-aversion of each agent in the economy. “Risk-neutral rates” are a theoretical construction that enables us to calculate rates as if nobody were risk-averse.

Many types of analysis in interest rate management require computing the expected value of a function of the interest rate. One example is to calculate the probability that portfolio loss is within a certain range. The probability of such an event is nothing but the expected value of the indicator function of this occurrence, which is worth one if the event is true and zero otherwise. Another example is to compute the market value of a derivative instrument.

In mathematical terms, the market value of a security that pays a cash flow at time T is equal to the expected value of the product of the stochastic discount factor at time T and the cash flow, that is:

Market Value = E [Discount Factor * Cash Flow]

where the stochastic discount factor is equal to the present value (along with a rate scenario) of one dollar received at time T. It is therefore a function of the rate.

The goal of term structure models is to forecast probability distributions of interest rates under which the expected value is defined.

Most term structure models used in practice, and all term structure models available in the system, are single-factor models of the short term interest rate. Short Rate modeling prevails because the problem of correlating multiple factors is greatly simplified. With single-factor models, the value in the future depends only on the value at the current time, and not on any previous data. This property is referred to as a Markov process.

Monte Carlo is the most popular numerical technique to compute an expected value, in our case market value and Value-at-Risk. The methodology consists of generating rate scenarios using random numbers, computing a function of the rates for each scenario, and then averaging it. Market value is the average across all scenarios of the sum of all cash flows discounted by the (scenario-specific) rate. Value-at-Risk is the maximum loss in value over a specific horizon and confidence level.

Monte Carlo simulation works forward from the beginning to the end of the life of an instrument and can accommodate complex payoffs, for instance, path-dependent cash flows. The other numerical methods, such as lattice and finite difference, cannot handle the valuation of these path-dependent securities. The drawback of Monte Carlo is its slow convergence compared to other methods. We address this problem by implementing better random sequences of random numbers, namely Low-Discrepancy Sequences. Monte Carlo has better performance than other techniques, however, when the dimension of a problem is large.

The architecture of the Rate Generator

The Rate Generator takes as input the information from the Rate Management tables (which include term structure parameters and smoothing technique, and risk-free yield curve yields), Product Characteristic assumptions (OAS), ALM Stochastic Process (risk-free yield curve, number of rate scenarios, risk period at which to compute VaR), Stochastic Rate Index rules (formulas for rate indices), and generates monthly rates and stochastic discount factors for each scenario and monthly bucket.

We take the benchmark securities to be zero-coupon bonds whose yields are stored in Rate Management and identified as the risk-free yield curve.

The Monte Carlo Rate Generator also calculates future rates (for a maturity other than one month) for each scenario and beginning at any month within the modeling horizon. These rates are used by the cash flow engine for repricing events and as market rates within the prepayment function.

The process flow of the Rate Generator depends on the type of term structure model. However, all processes share the same building blocks.

Computation of Rates and Stochastic Discount Factors

At the beginning of an ALM Process, the Rate Generator calculates and stores monthly rates for 360 months and all scenarios.

Upon request by the Cash Flow engine, the Rate Generator will calculate the rate, that is, the annually compounded yield at any time T for a discount bond maturing at time T, as follows:

·        Compute the future bond price using a closed-form solution (a discretized version of Hull and White solution.)

·        Convert discount bond prices into discrete yields.

We limit the simulation horizon to 30 years from the As-of-Date. After that period, rates are set equal to the 30-year rate. Also, the closed-form formula is limited to a 30-year term. Rates with a longer-term are set equal to the 30-year term rate.

The cash flow engine may need rates from another IRC (Index) than the risk-free IRC. In this case, the value of the Interest Rate Code (IRC) with maturity T will be a function of the value of the risk-free IRC.

The Rate Generator pre-computes the stochastic discount factor for every scenario, for the first day of every monthly bucket. The computation can be selected with or without an Option Adjusted Spread (OAS) added. The OAS depends on the Product Dimension member and is expressed in terms of discrete annual compounding rate. For internal code optimization reasons, we limit the maximum OAS value to 5%.

Arbitrage Term Structure Model

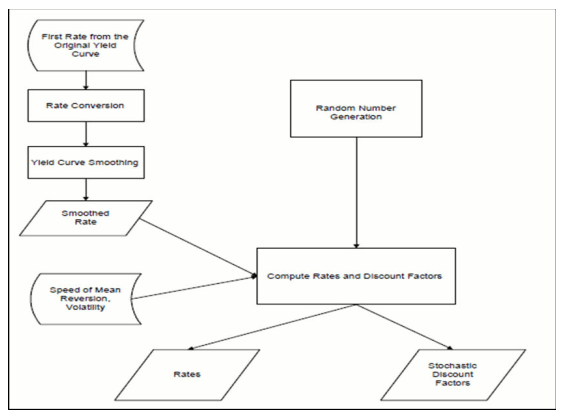
Arbitrage models (Merton and Vasicek) use the first-rate from today's yield curve (smoothed and converted to continuous compounding, as described later in the section). It feeds directly the Rate Generator along with the term structure parameters to produce monthly rates, stochastic discount factors for each scenario and month, and discrete rates for any maturity.

The following diagram shows the process flow for Vasicek (or Merton) models in the Rate Generator:

Description of process flow for Vasicek (or Merton) models follows

The disadvantage of these models is that they do not automatically fit today's term structure. The parameters can be chosen so that arbitrage models provide a close fit to many of the real yield curves, but the fit is usually not exact and often gives significant errors.

To achieve no-arbitrage conditions, the model itself can be used to calibrate the parameters of the model. Given the prices of benchmark securities, the model finds the rate probabilities such that, when they are used as input to the pricing tool, the output will be as close as possible to the original prices.

No-Arbitrage Term Structure Models

The no-arbitrage models (Ho and Lee and Extended Vasicek) are designed to fit the current term structure of interest rates exactly. This is achieved when the price of a zero-coupon bond computed through the Monte Carlo process exactly matches today's observable market rates, as defined by the risk-free curve selection. The market price of risk is a function of time that takes care of this fit.

To adhere to this condition, the process flow for no-arbitrage models is more complicated. A trinomial lattice is used to compute the market price of risk to calibrate the term structure. The full original As-of-Date yield curve is used, smoothed and converted to continuous compounding, to be fed into the lattice.

Description of process flow for Vasicek (or Merton) follows

Yield Curve Smoothing

Today's yield curve from an OFSAA Rate Management IRC might not have enough terms for a term structure model to give the best rates forecast. In particular, the trinomial lattice needs the value of the yield for every month. To do this, two smoothing techniques have been introduced into the Rate Generator: Cubic Spline and Linear Interpolation.

Calibration

Hull and White have shown how trinomial trees (lattice) can be used to value interest rate derivatives. The goal of the trinomial lattice is to compute the market price of risk for all buckets for the Ho and Lee or Extended Vasicek (no-arbitrage) term structure models.

Hull and White's lattice is a popular methodology to calibrate a term structure model. The lattice is constructed for up to 360 monthly buckets, from bucket zero to either (the last maturity on the IRC + 15 years) or 30 years, whichever is shorter.

Random Number Generation

To model a discrete-time stochastic process using the Monte Carlo method we need to use some random variables. Numbers generated by computers are not truly random. Standard random number generators produce uniformly distributed pseudo-random numbers that are made to have the statistical properties of truly random numbers.

Non-uniform variables are sampled through the transformation of uniform variables. There are several methods developed for this purpose, both general (to produce random variables of a given density) and special (to directly generate normal random variables): transformation, acceptance-rejection, Box-Muller, and so on. We use the so-called “polar algorithm” technique.

You have a choice to use Low Discrepancy Sequences (LDS), also called quasi-random numbers, as a substitute to pseudo-random numbers. One more important feature of LDS is to reach the consistency across all computers in generating rate paths (pseudo-random numbers generated by different machines are different).

Low Discrepancy Sequences

Low Discrepancy Sequences, also called quasi-random numbers, are a recent substitute to the traditional random numbers used by all compilers (usually called pseudo-random numbers). They were introduced in the '50s and '60s by mathematicians like Halton, Sobol, and Niederreiter. The theory and implementation of low discrepancy sequences have enjoyed tremendous progress in the past 10 years, and they are now becoming increasingly popular in the area of financial mathematics.

The main objective of low discrepancy sequences is to reduce the error of Monte Carlo methods. Because the error in Monte Carlo methods decreases with the number of scenarios, we can also state that Monte Carlo with LDS needs fewer scenarios than traditional Monte Carlo to obtain the same result. Therefore, Monte Carlo with LDS should be faster than traditional Monte Carlo.

Rate Conversion

There are two major procedures applied by the Rate Generator to the original risk-free rates from the Rate Management IRC: timescale conversion and compounding basis conversion.

Timescale Conversion

We introduced two timescales, the normal timescale, and the equal-month timescale, to satisfy three requirements:

·        Monthly buckets have to be an integer number of days in length because the cash flow engine works on a daily timescale.

·        Performance should generate rates with an equal-month timescale.

·        We cannot set the bucket length to be 30 days, because buckets will start 5 days earlier each year, and this conflicts with reporting requirements.

The equal-month timescale is used only internally in the Rate Generator. It assumes that each month is constant and is equal to 1/12 of a year. The normal timescale counts the actual number of days, that is, each monthly bucket has a different length. In other words, the normal timescale assumes an Actual/Actual day count basis, whereas the equal-month timescale assumes a 30/360 count basis. The convention is the regular Oracle ALM convention for a month: if bucket zero starts on day n then all next buckets start on day n except when this day does not exist (February 30 for instance), in which case it reverts to the last existing day of the month (for example, February 28).

There is a one-to-one relationship between the timescales.

Let us suppose that the As-of-Date is January 15, 2011. By definition, every bucket will then start on the 15th of that corresponding month.

In this example, the discrete yield (quoted Actual/Actual) is constant. However, the 2-month smoothed yield is lower than the 1 month smoothed yield because the timescale transformation overestimates the length of the second month.

Compounding Basis Conversion

The Monte Carlo process requires annually compounded Actual/Actual zero-coupon yields as the input. If the input IRC format is different from that, a rate conversion process is applied.

Also, the Rate Generator converts rates from the yield curves (which are discretely compounded, on the normal timescale) into continuously compounded rates on the equal-month timescale. This conversion has to be done for all the points in today's yield curve.

The Rate Generator always uses the latest yield curve from the Rate Management IRC and assumes that the same yield curve prevails at the As-of-Date. Monte Carlo simulation always starts from the As-of-Date.

Output From Monte Carlo

The amount of data to be output in a Monte Carlo processing run depends on the type of processing and the requirements of the users. A stochastic process using Monte Carlo provides the following results:

·        Market value at the dimension member level

·        Value-at-Risk at the dimension member level

·        Value-at-Risk at the portfolio level

The smallest set of output will result from the market value processing run. Market value is the average across all scenarios of the sum of all cash flows discounted by the (scenario-specific) rate.

The output will be a single value - the market value per dimension member - stored in the FSI_O_STOCH_MKT_VAL table. The table has a simple structure:

Value-at-Risk (VaR) is the maximum loss in value over a specific horizon (risk period) and confidence level. The horizon is specified by the user. Unlike many other products, Oracle ALM outputs VaR for any confidence level, that is, it outputs the full probability distribution of loss for each Product COA member. The output is written to the FSI_O_STOCH_VAR table:

The system will also output VaR at the portfolio level (into the FSI_O_STOCH_ TOT_VAR table). In this example, we assume that our portfolio has only deposits and fixed mortgages.

As you can see from the following graph, the total VaR does not necessarily equal the sum of the VaR for each portfolio because of the correlation between mortgages and deposits.

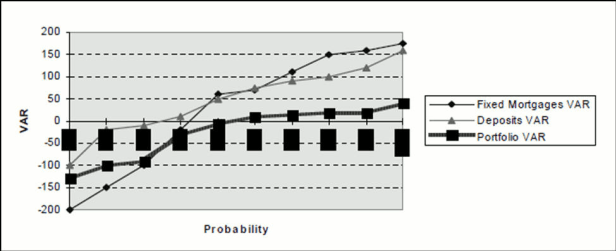
Description of graph for Output From Monte Carlo follows

We selected the Monte Carlo method to implement VaR over other methods such as J.P. Morgan's RiskMetrics approach because of the following advantages:

·        Better accuracy in analyzing nonlinear assets such as options.

·        More flexibility to model the distribution of economic factors versus normal assumption in RiskMetrics.

·        No need to decompose securities into “risk factors”; a complicated process for fixed income.

Oracle ALM also provides auditing options. Monthly rates correspond to yields of a risk-free zero-coupon bond with a maturity of one month. These rates are used for all other calculations in the stochastic Rate Generator. They are output into the FSI_INTEREST_RATES_AUDIT table, where the values are displayed for each scenario and every time step, that is, up to 2,000 scenarios times 360-time steps. Because of the amount of data being written, this process can be very time-consuming.

Cash flows are also available for auditing purposes if the Detail Cash Flow option is selected in the Stochastic ALM Process. For more details on this process, see �Detail Cash Flow Audit Options.

The stochastic discount factors are also output as an auditing feature. This is extremely valuable for testing purposes. The user can check this output any time the “Detail Cash Flow” output option is on. The table used is called FSI_O_PROCESS_CASH_FLOWS, Financial Element 490.

VaR Output Including Liabilities

This section explains how to interpret the meaning of the Value-at-Risk (VaR) output from Oracle ALM when the balance sheet includes liabilities. We will specifically explain the difference between the output on the product level (as stored in the FSI_O_STOCH_VAR table) from the output on the balance sheet level (as stored in the FSI_O_STOCH_TOT_VAR table). For simplicity, let us consider a simple balance sheet with only one liability instrument and five rate scenarios.

An Example: Product Versus Balance Sheet Level Results

Let us assume that for the 1 liability instrument, Oracle ALM calculates a market value of $100,000 and the following accrued dynamic present values for each scenario:

Though the actual value to the bank is -$100,000, Oracle ALM by convention reports a positive market value for all instruments. Therefore, it is important to remember that positive market value for liability is in effect a loss. The same convention applies to VaR. Though VaR is defined as the "maximum loss (to the bank)", it must be substituted with “maximum gain (to the bank)” when interpreting the VaR output for an instrument that is a liability.

Assume Oracle ALM outputs the first three columns of the following table to the FSI_O_STOCH_VAR table for the 1 liability product. Recall that FSI_O_STOCH_VAR contains product level output. When interpreting the VaR output for liability on a product output level, you must remember that VaR is the "maximum gain (to the bank)".

The discrete probability of a gain of exactly -$26,408, -$24,733, $8,808, $17,957, $23,149 is 20% for a 5 scenarios simulation.

NOTE:   

The sum of all probabilities adds up to a total of 100% probability.

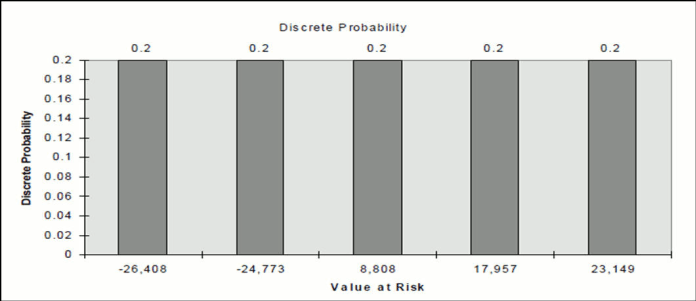
Description of graph of discrete probability follows

In Value at Risk interpretation, we need to convert the discrete probability to a cumulative distribution function. For example, we know that there is a chance of a gain of -$26,408 with a probability of 20% and a gain of -$24,773 with a probability of 20%. This means that there is a 40% probability of gain less than or equal to -$24,773. This comes from adding a 20% discrete probability from the gain of $-26,408 and a 20% discrete probability from a gain of -$24,773.

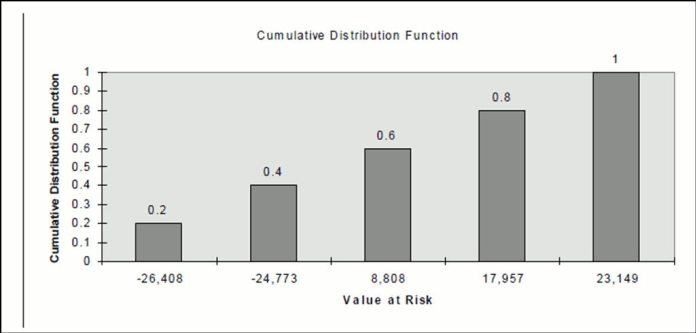
Description of graph of cumulative distribution function follows

Now let's assume Oracle ALM outputs the first three columns of the following table to FSI_O_STOCH_TOT_VAR table for the 1 liability product. Recall that FSI_O_STOCH_TOT_VAR contains a balance sheet level output. At the balance sheet level, we aggregate gain/loss information for different products that can be either assets or liabilities. Oracle ALM by convention reports the aggregated VaR number as a “maximum loss”; therefore, the sign of VaR for all liabilities must be reversed.

Validating Interpretation

Let us analyze the most beneficial scenario (to the bank) to prove that our interpretation is correct. In scenario 5, the “gain = 23,149” has a probability of 20% because it is a discrete event. We also have the following events and probabilities:

When we apply the signage to liability, the discrete probability is undisturbed for each event.

NOTE:   

Each event still has a discrete probability of 20%

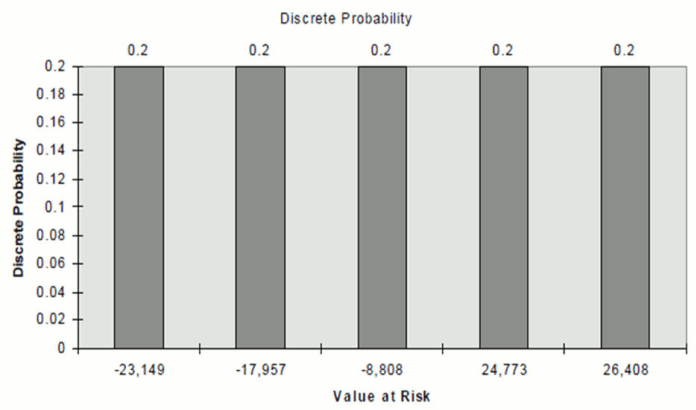
Description of graph of discrete probability follows

We see here that there is a 20% probability of a maximum loss of -$23,149. There is a 40% probability of a maximum loss of -$23,149 (20% discrete probability from -$23,149 plus 20% discrete probability from -$17,957).

Description of graph of cumulative distribution function follows

The event “gain<  23,149” corresponds to the union of these two events:

“gain < 23,149”

“gain = 23,149”

Because these two events are disjoint - making each event's probability discrete – the probability that “gain ≤ 23,149” is the sum of their respective probabilities. It is equal to 80%+20%=100% as reported in the FSI_O_STOCH_VAR table.

The event “loss ≤-23,149” on the other hand corresponds to the union of these two events:

“loss = - 23,149”, that is, “gain = 23,149”

“loss < - 23,149”, that is, “gain > 23,149”

Because these two events are also disjoint - making each event's probability discreet - the probability that “loss ≤ -23,149” is the sum of their respective probabilities. It is equal to 20%+0%=20% as reported in the FSI_O_STOCH_TOT_VAR table.

Value-at-Risk

In our current implementation, Value-at-Risk is the worst loss of present value over an At-Risk period (time horizon), given a confidence level. The maximal At-Risk period is 10 years.

Oracle ALM outputs Value-at-Risk for as many confidence levels as there are scenarios in Monte Carlo simulation. In other terms, it outputs the full present value loss probability distribution and its inverse, which are much richer statistics than a single VaR number.

The following section describes our current approach to estimating Value-at-Risk.

Present Value-at-Risk

The approach is as follows:

1.     For each scenario, compute the accrued dynamic present value by dividing the (scenario-specific) present value by the stochastic discount factor; we do not take the new business into account.

2.     For each scenario, compute VaR as market value minus accrued dynamic present value.

3.     Sort VaR in ascending order and output it along with its normalized ranking (that is, the ranking divided by the total number of scenarios).

The normalized ranking is an unbiased estimator of the probability that loss of value is less than VaR, that is, each couple of values (normalized ranking, VaR) is a point on the loss probability distribution curve.

Illustration of the Approach

We have only 10 scenarios. Today's market value is $80.

After sorting we have:

Varying the At-Risk Period

This example tries to give intuition behind the numbers by varying the At-Risk period for a typical case. The instrument we analyze is a two-year discount bond with a principal of $100. The market value is $78.

To ease comprehension of the graph, we display the probability mass function and not the cumulative probability distribution.

Description of graph of probability mass function follows

This graph reflects two important features of a fixed-rate instrument:

·        On average, VaR decreases with time because the dynamic present value increases with time.

·        The dispersion of VaR goes to zero when approaching maturity.

Earnings-at-Risk

Earnings-at-Risk is a methodology for income sensitivity that combines the Monte Carlo Rate Generator with the cash flow engine to produce statistical information about forecasted income. Earnings-at-Risk functionality uses the stochastic processing methodology to provide users with a probabilistic view of forecasted earnings for individual products and the entire balance sheet. The probability distribution of earnings enables users to view expected income as well as the potential loss of income in the future due to interest rate fluctuations. With this information, users can efficiently determine what is likely to happen as well as identify the scenarios that may provide the greatest risks to the institution.

An Earnings-at-Risk process reads records from the following sources:

·        Instrument data

·        Transaction Strategy

·        Forecast Balance

Cash flows are calculated for each record, for every rate path generated by the Rate Generator. Earnings results may include the following financial data, depending on the account type of the product:

·        Net interest accrual

·        Deferred runoff

·        Non-interest income

·        Non-interest expense

·        Dividends

·        Taxes

The following four sets of output data are available after an Earnings-at-Risk processing run, for each modeling bucket as defined in the active Time Bucket definition:

·        Average income overall rate paths for each product

·        Average income overall rate paths for the entire bank

·        Income in each rate path for each product

·        Income in each rate path for the entire bank

From the preceding list, the average income data sets are output for every Earnings-at-Risk process. The other two output sets are optional and may be selected as part of the process definition.

The output is stored in the following tables:

·        EAR_LEAF_DTL_xxx - (optional) Earnings are aggregated by product and stored for each rating scenario.

NOTE:   

Earnings are equivalent to net interest accrual in scenario-based processing.

·        EAR_LEAF_AVG_xxx - Average earnings are calculated for each product by taking the simple average across all rate paths for each modeling bucket.

·        EAR_TOTAL_DTL_xxx- (optional) Both net interest income and net income values are calculated, aggregated across products, and stored for every rate scenario per modeling bucket. Net interest income is calculated as interest income less interest expense. Net income is calculated as net interest income and non-interest income combined, less non-interest expense, fewer taxes, if applicable.

·        EAR_TOTAL_AVG_xxx - Net interest income and net income values as described earlier are averaged across all rate paths for each modeling bucket.

Also, the initial balances and rates are output to FSI_O_RESULT_MASTER based on the instrument records being processed. This records information on each product such as the par balance, deferred balance, weighted current rates, and weighted average remaining maturity.

As with any stochastic process, users have the option to output audit results for cash flows and rates (For more information on Audit in ALM Processing, see Oracle Financial Services Asset Liability Management User Guide.)

NOTE:   

Historical/Monte Carlo simulation is a single factor modeling of interest rates of Reporting Currency. Although the engine does convert Balances into Reporting Currency, there is no correlation of Risk factors of particular Currency’s Interest rates with Reporting Currency. Stochastic processing is not intended for Multi-currency processes. For best results, run Historical/ Monte Carlo calculation for a Single currency where Functional Currency = Reporting Currency.

Recommended Configuration

For maximum precision, use the following settings in a Stochastic ALM Process rule:

·        Extended Vasicek term structure model

·        The cubic Spline smoothing technique

·        Low Discrepancy Sequences

·        2,000 rate scenarios

NOTE:   

This is the recommended configuration for precision. Because 2000 scenarios may require a significant amount of computing time, the user may prefer to lose some precision by selecting fewer scenarios.

The following section attempts to explain some criteria and issues related to choosing the optimal configuration for stochastic processing.

Term Structure Models

Select the Extended Vasicek model for the computation of market value and Value-at-Risk.

You have a choice of four-term structure models:

4.     Merton (requires only the parameter volatility to be specified).

5.     Vasicek (requires all three parameters to be specified: mean reversion speed, volatility, and long-run rate).

6.     Ho and Lee (requires only the parameter volatility to be specified).

7.     Extended Vasicek (requires to mean reversion speed and volatility parameters to be specified).

Merton Model

One simple assumption about interest rates is that they follow a simple random walk with a zero drift. In stochastic process terms, we would write the change in r as:

Description of formula to calculate the dr for Merton Model follows

The change in the short rate of interest r equals a constant sigma time a random shock term where Z represents a standard Wiener process with mean zero and standard deviation of 1.

This model has the following virtues and liabilities:

·        It is a simple analytical formula.

·        Zero-coupon bond prices are a quadratic function of time to maturity.

·        Yields turn negative (and zero-coupon bond prices rise above one) beyond a certain point.

·        If interest rate volatility is zero, zero-coupon bond yields are constant for all maturities and equal to r.

The Merton model gives us very important insights into the process of deriving a term structure model. Its simple formulas make it a useful expository tool, but the negative yields that result from the formula are a major concern.

Ho and Lee Model

Ho and Lee extended the Merton model to fit a given initial yield curve perfectly in a discrete-time framework. In the Ho and Lee model case, we assume that the short rate of interest is again the single stochastic factor driving movements in the yield curve. Instead of assuming that the short rate r is a random walk, however, we assume that it has a time-dependent drift term θ(t) :

Description of formula to calculate the dr for Ho and Lee Model follows

As before, Z represents a standard Wiener process with mean zero and standard deviation of 1.

By applying the no-arbitrage condition, the function q(t) is chosen such that the theoretical zero-coupon yield to maturity and the actual zero-coupon yield are the same. The function q(t) is the plug that makes the model fit and corrects for model error, which would otherwise cause the model to give implausible results. Because any functional form for yields can be adapted to fit a yield curve precisely, it is critical, in examining any model for plausibility, to minimize the impact of this extension term. The reason for this is that the extension term itself contains no economic content.

In the case of the Ho and Lee model, the underlying model would otherwise cause interest rates to sink to negative infinity, just as in the Merton model. The extension term's magnitude, therefore, must offset the negative interest zero-coupon bond yields that would otherwise be predicted by the model. As maturities get infinitely long, the magnitude of the extension term will become infinite in size. This is a significant cause for concern, even in the extended form of the model.

Vasicek Model

Both the Merton model and its extended counterpart the Ho and Lee model are based on an assumption about random interest rate movements that imply that, for any positive interest rate volatility, zero-coupon bond yields will be negative at every single instant in time, for long maturities beyond a critical maturity t. The extended version of the Merton model, the Ho and Lee model, offsets the negative yields with an extension factor that must grow larger and larger as maturities lengthen. Vasicek  proposed a model that avoids the certainty of negative yields and eliminates the need for a potentially infinitely large extension factor. Vasicek accomplishes this by assuming that the short rate r has a constant volatility sigma like the models as mentioned earlier, with an important twist: the short rate exhibits mean reversion:

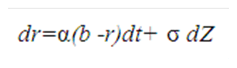
Description of formula to calculate the dr for Vasicek Model follows

where:

r is the instantaneous short rate of interest

α  is the speed of mean reversion

b is the long-run expected value for rate

σ is the instantaneous standard deviation of r

Z is the standard Wiener process with mean zero and standard deviation of 1. The stochastic process used by Vasicek is known as the Ornstein-Uhlenbeck process. This process enables us to calculate the expected value and variance of the short rate at any time in the future s from the perspective of current time t.

Because r(s) is normally distributed, there is a positive probability that r(s) can be negative. As pointed this is inconsistent with a no-arbitrage economy in the special sense that consumers hold an option to hold cash instead of investing at negative interest rates. The magnitude of this theoretical problem with the Vasicek model depends on the level of interest rates and the parameters chosen (In general, it should be a minor consideration for most applications). The same objection applies to the Merton and Ho and Lee models and a wide range of other models that assume constant volatility of interest rates, regardless of the level of short term interest rates. Very low-interest rates in Japan in early 1996, with short rates well under 0.5%, did lead to high probabilities of negative rates using both the Vasicek and Extended Vasicek models when sigma was set to match observable prices of caps and floors. Although the price of a floor with a strike price of zero was positive during this period (indicating that the market perceived a real probability of negative rates), the best fitting values of sigma for all caps and floor prices indicated a probability of negative rates that was unrealistically large.

NOTE:   

Lehman Brothers were quoting a floor on six-month yen LIBOR with a three-year maturity and a strike price of zero at 1 basis point bid, 3 basis points offered during the fall, 1995.

For most economies, Vasicek and Extended Vasicek models are very robust with wide-ranging benefits from practical use.

Extended Vasicek (Hull and White) Model

Hull and White bridged the gap between the observable yield curve and the theoretical yield curve implied by the Vasicek model by extending or stretching the theoretical yield curve to fit the actual market data. A theoretical yield curve that is identical to observable market data is essential in practical application. A model that does not fit actual data will propagate errors resulting from this lack of fit into hedge ratio calculations and valuation estimates for more complex securities. No sophisticated user would be willing to place large bets on the valuation of a bond option by a model that cannot fit observable bond prices.

Hull and White apply the identical logic as described in the previous section, but they allow the market price of risk term to drift over time, instead of assuming it is constant as in the Vasicek model. This could be written as:

Description of formula to calculate the dr for Extended Vasicek Model follows

where:

r is the instantaneous short rate of interest

is the speed of mean reversion

is the instance standard deviation of r

is the market price of risk for time t

As noted earlier, the Extended Vasicek (Hull and White) model is currently the most popular term structure model. It has a clear economic meaning and is computationally very robust. Because of its popularity, numerous studies have documented and continue to document what parameters (speed of mean reversion and volatility) should be used. Another advantage of the Extended Vasicek model is that bond prices have an easy closed-form formula. This closed-form formula leads to a very fast computation of rates for any term inside Monte Carlo simulation.

Term Structure Parameters Format

As mentioned in the preceding sections, speed of mean reversion, volatility, and long-run rate are the parameters the user will have to specify for the chosen model. Speed of Mean Reversion represents the long-run drift factor (1/mean reversion = interest rate cycle). Volatility is the standard deviation of the one-month rate, annually compounded on the equal-month timescale. Long Run Rate (b) represents the equilibrium value of the one-month rate, annually compounded.

Sometimes α and σ are available from external sources, but they are quoted differently. The following equations show how to obtain the “one-month” speed of mean reversion and volatility from the values of α and s corresponding to:

instantaneous rate, αi(αi and σi hereafter)

rate with term ∆t years (α ∆t and σ∆t hereafter)

(For clarity we write α1m and α1m for the one-month parameters)

Description of formula to calculate the Term Structure Parameters Format  follows

The following graph shows the change in the ratio σ1m/ σivarying Dt (αi = 0.1):

Description of graph of change in the ratio σ1m/ σivarying Dt (αi = 0.1) follows

Though the decision on the best choice for the term structure parameters is left to the user, the software imposes certain restrictions on those as follows:

0 < α<1

0.01%< σ <10%

0% < b < 200%

One more restriction has been set on the parameter combination for no-arbitrage models:

(σ-23α) > 0.7

If this inequality does not hold, the system outputs a warning message and continues processing. Be aware that the resulting rates may not be fully no-arbitrage if the yield curve is very erratic.

Estimating Term Structure Parameters

Many discussions of the use of term structure models in risk management overlook the difficulties of estimating the parameters for such models. Market participants have become used to the idea of estimating parameters from observable market data through the popularity of the Black-Scholes option pricing model and the accepted market practice of estimating volatility for use in the model from market option prices.

“Implied volatility” is the value of volatility in the Black-Scholes model that makes the theoretical price equal to the observable market price.

Treasury Services Corporation (since acquired by Oracle in September of 1997) and Kamakura Corporation made an in-depth analysis of this parameter estimation problem. The analysis was based on the data set that includes 2,320 days of Canadian Government Bond data provided by a major Canadian financial institution. The data spanned the period January 2, 1987, to March 6, 1996. In the last section, American swaption data provided by one of the leading New York derivatives dealers is used.

Estimating procedures for term structure models have not progressed as rapidly as the theory of the term structure itself, and leading-edge practice is progressing rapidly. There is a hierarchy of approaches of varying quality to determine the appropriate parameters.

Traditional Academic Approach

This approach follows theory precisely to estimate the stochastic process for the short term risk-less rate of interest, in this case, the one-month Canadian government bill yield. This approach is generally not satisfactory in any market and was found to be unsatisfactory with Canadian data as well.

For an example of a well-done analysis of the parameters of several theoretical models, see Chan, Karolyi, Longstaff, and Sanders [4]. The study, while well done, suffers from the typical outcome of such studies: in no case does the assumed stochastic process explain more than three percent of the variation in the short term rate of interest. We find the same problem when running the regression on 2,320 days of data using the one-month Canadian bill rate as the short rate proxy. It is concluded that this approach is not useful in the Canadian market because of the lack of correlation between the level of interest rates and change in the level of the short rate.

Volatility Curve Approach

This approach matches parameters to the historical relative volatilities of bond yields at different maturities. This approach worked moderately well.

Many market participants use parameter estimates that are consistent with the historical relative degree of volatility of longer-term “yields” about the short rate. Market participants calculate observable variances for bond yields and then select values of s and α that best fit historical “volatility.” The findings for the Canadian Government Bond market were based on the use of par bond coupon rates as proxies for zero-coupon bond yields. The results of this analysis are summarized in the following table:

Example: Variance in Canadian Government Interest Rates January 2, 1987, to March 6, 1996

NOTE:   

Interest Rates and Variances are in %.

The best-fitting α value was 0.305. This is a fairly large speed of mean reversion and reflects the relatively large variation in short term Canadian rates, relative to long rates, over the sample period. Interest rate volatility was also high at .0285. At the 1996 low levels of Canadian interest rates, this volatility level would be too high. Comparable figures for the United States swap market, based on a fit to 100 swaptions prices, reflected a speed of mean reversion of 0.05 and an interest rate volatility of 0.013.

Advanced Historical Volatility Approach

This approach fits relative yield changes on all 2,320 days based on the theoretical relationship between the short rate and longer-term yields by regression analysis and then fits term structure model parameters to the regression coefficients.

For the Canadian market, a regression of par bond coupon yields (as proxies for zero-coupon bond yields) on the one-month Canadian Government bill rate was performed. The results of this regression showed a higher implied mean reversion speed at shorter maturities.

Implied Speed of Mean Reversion by Historical Sensitivity to Movements in the Canadian Treasury Bill Rate (1987 - 1996)

The best-fitting α at three years was a very high 1.00921. At 25 years, the α at 0.296 is much more consistent with the historical variances. This chart provides a strong indication that a two-factor model would add value in the Canadian market (assuming other problems, like parameter estimation and the valuation of American options that are strong disadvantages of two-factor models). This is true of most markets where recent interest rate fluctuations have been large and where current rate levels are near historical lows. The Australian market has had similar experiences.

Single-Day Yield Curve Fitting

This approach is the yield curve equivalent of "implied volatility" using Black-Scholes. Most market participants feel more comfortable basing the analysis on parameter values implied from observable securities prices than on historical data when observable prices are sufficient for this task. For example, if the only observable data is the yield curve itself, we can still attempt to fit the actual data to the theory by maximizing the goodness of fit from the theoretical model.

We arbitrarily set the market price of risk to zero and the long-run expected value of the short rate to equal the ten-year bond yield. They then find the best fitting α and s. The result is generally of marginal acceptability. This is a common conclusion, as pointed out by the former head of derivatives research at Merrill Lynch, and one of the reasons why market participants often feel compelled to supplement current yield curve data with historical parameter data.

To illustrate the yield curve fitting approach, we took yield curve data for the beginning, middle, and end of the data set and picked the days for which the ten-year Canadian government bond yield reached its highest and lowest points. The following maturities have been used: one-month, six-months, two, three, four, five, seven, and ten years. The results of this analysis, using simple spreadsheet software to obtain parameters, were as follows:

·        Best Fitting Parameters from Selected Yield

·        Canadian Government Bond Market

·        Extended Vasicek Model

·        Using Common Spreadsheet Non-Linear Equation Solver

NOTE:   

Spreadsheet solver capabilities are limited. The market price of risk and the long-run rate was arbitrarily set to displayed values with optimization speed of mean reversion and volatility.

The results were consistent with other approaches in generally showing a high degree of mean reversion. The lack of power in spreadsheet non-linear equation solving is reflected in the low or zero values for interest rate volatility and illustrates the need for other data (caps, floors, swaptions, bond options prices, and so on) and more powerful techniques for obtaining these parameters.

The Best Approach

Given these results, we think it is essential to use parameters estimated from observable caps, floors, and swaptions data (or other option-related securities prices) to the extent it is available. To illustrate the power of this approach, consider now the U.S. dollar data on European swaption prices observable in August 1995. At the time the data were obtained, there were 54 observable swaption prices. A swaption gives the holder the right to initiate a swap of a predetermined maturity and fixed-rate level on an exercise date in the future. We estimated Extended Vasicek model parameters by choosing the speed of mean reversion (α) and interest rate volatility (s), which minimized the sum of the squared errors in pricing these 54 swaptions. The “price” of the swaption was obtained by converting the Black-Scholes volatility quotation for the swaption price to the percentage of notional principal that the equivalent dollar swaption price represented. The exercise periods on the swaptions were 0.5, one, two, three, four, and five years. The underlying swap maturities were 0.5, one, two, three, four, five, six, seven, and ten years.

Overall, the Extended Vasicek model's performance was extraordinary. The average model error was 0 basis points with a mean absolute error of five basis points of notional principal, even though only two parameters (in addition to the current yield curve) were used to price 54 securities. Compare this to the Black model for commodity futures, which is often used for swaptions and caps and floor pricing. The Black model required 54 different implied volatility values to match actual market prices, even though the model, in theory, assumes that one volatility parameter should correctly price all 54 swaptions. Volatilities in the Black model ranged from 0.13 to 0.226, a very wide range that should indicate to swaption market participants the need for caution.

In summary, the extended version of the Vasicek model, when applied to swaption prices, proved two things:

·        Swaptions provide a rich data set with excellent convergence properties that enable market participants to use even common spreadsheet software to obtain high-quality term structure parameter estimates.

·        The accuracy of the Extended Vasicek model using only two parameters held constant over 54 swaptions, is far superior to that of the Black commodity futures model in predicting actual market prices.

In estimating term structure parameters, the lesson is clear. A rich data set of current prices of securities with significant optionality is necessary to provide an easy-to-locate global optimum for almost any popular term structure model.

Choosing a Smoothing Method

One of the most fundamental steps in fixed-income option valuation is calculating a smooth yield curve. The original yield curve from the Rate Management IRC may not have enough terms for the term structure parameter estimation routine to work properly. In particular, the trinomial lattice needs the value of the yield for every bucket point.

The simple description of smoothing is to draw a smooth, continuous line through observable market data points. Because an infinite number of smooth, continuous lines pass through a given set of points, some other criterion has to be provided to select among the alternatives. There are many different ways to smooth a yield curve. The best technique is the one that results in the best term structure parameters.

The Rate Generator has two different smoothing techniques:

·        Cubic Spline

·        Linear Interpolation

Cubic Spline of Yields

One approach to smoothing yield curves is the use of cubic splines. A cubic spline is a series of third-degree polynomials that have the form:

Description of formula to calculate the Cubic Spline of Yields follows

where:

x = years to maturity (independent variable)

y = yield (dependent variable)

These polynomials are used to connect-the-dots formed by observable data. For example, a US Treasury yield curve might consist of interest rates observable at 1, 2, 3, 5, 7, and 10 years. To value a fixed-income option, we need a smooth yield curve that can provide yields for all possible yields to maturity between zero and 10 years. A cubic spline fits a different third-degree polynomial to each interval between data points (0 to 1 year, 1 to 2 years, 2 to 3 years, and so on). In the case of a spline fitted to swap yields, the variable x (independent variable) is years to maturity and the variable y (dependent variable) is yield. The polynomials are constrained so they fit together smoothly at each knot point (the observable data point); that is, the slope and the rate of change in the slope to time to maturity have to be equal for each polynomial at the knot point where they join. If this is not true, there will be a kink in the yield curve (that is, continuous but not differentiable).

However, two more constraints are needed to make the cubic spline curve unique. The first constraint restricts the zero-maturity yield to equal the 1-day interest rate (for example, the federal funds rate in the U.S. market). At the long end of the maturity spectrum, several alternatives exist. The most common one restricts the yield curve at the longest maturity to be either straight (y"=0) or flat (y'=0). There are other alternatives if the cubic spline is fitted to zero-coupon bond prices instead of yields.

Our function will also extrapolate the original yield curve outside its domain of definition. The resulting smoothed yield curve will be constant and equal to:

·        the first term yield for T ≤ first term

·        the last term yield for T  ≥ last term

Linear Interpolation

Cubic splines have historically been the method preferred for yield curve smoothing. Despite the popularity of the cubic spline approach, market participants have often relied on linear yield curve smoothing as a technique that is especially easy to implement, but its limitations are well-known:

·        Linear yield curves are continuous but not smooth; at each knot point, there is a kink in the yield curve.

·        Forward rate curves associated with linear yield curves are linear and discontinuous at the knot points. This means that linear yield curve smoothing sometimes cannot be used with the Heath, Jarrow, and Morton term structure model because it usually assumes the existence of a continuous forward rate curve.

·        Estimates for the parameters associated with popular term structure models like the Extended Vasicek model are unreliable because the structure of the yield curve is unrealistic. The shape of the yield curve, because of its linearity, is fundamentally incompatible with an academically sound term structure model. Resulting parameter estimates are, therefore, often implausible.

NOTE:   

As in the case of the cubic spline, we extrapolate for the maturities less than the first term yield and greater than the last term yield: in the former, the yield is set to be equal to the first term yield, and for the latter, it is set to be the last term yield.

Defining a Rate Index Formula

The purpose of the Stochastic Rate Index assumption rule is to define a forecast of the index rates (such as Libor or Prime) based on the Monte Carlo forecast of the risk-free rate. This forecast is applicable for every time t in the future and every scenario.“Future” means any time after the As-of-Date.

The rate index primarily should be defined under the following situations:

·        The index is a contractual function of the risk-free yield.

·        The index is defined through a conjunction of exogenous factors, in which case time series analysis finds the best formula.

In this section, we analyze one important special case of a contractual function, namely how to translate simple rates (zero-coupon yields) into par bond coupon rates for a risk-free bond with one payment. We first describe the general formula a user can enter.

General Case

The user can enter the following formula for each index and index term:

Description of formula to calculate the each index and index term follows

where:

ai are coefficients, ai Š 0

bi are exponents; they can be integer only

ω refers to the Monte Carlo scenario

Tk is the term of the index for which the formula applies

τi is the term of each forecasted risk-free rate

R(t,t+τi,ω) is the risk-free rate at time t for a term of τi

In this formula, we included the scenario ω for notational convenience, although it cannot be specified by the user: the same formula is applied for each scenario - what varies is the risk-free rate. The user can specify only ai, bi, Tk,τi, and of course of the identity of the Index IRC for which the formula applies.

If an adjustable instrument in the database is linked to an index term for which the user did not define a formula, the engine will linearly interpolate (or extrapolate) along with the term.

Suppose the user-defined formulae only for Libor 1 month and Libor 5 months, but an instrument record is linked to Libor 3 months, the engine will calculate the index rate for Libor 3 months as the average of Libor 1 month and 5 months.

The formula for a Coupon Rate

Suppose that the security is issued at time t and pays T year(s) after it has been issued. A typical example would be a 6-month T-bill, that is, T=0.5. The owner of the security will receive at time t+T:

Description of formula to calculate the cash flow follows

where c is the unknown (annual) coupon rate. In a no-arbitrage economy this cash flow should be equal to:

Description of formula to calculate the future value of principle follows

Solving for the coupon rate gives the equation:

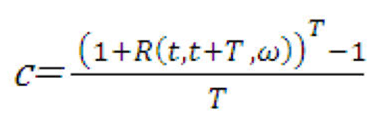
Description of formula to calculate the coupon rate follows

Because yields are usually much smaller than 100%, we can expand the numerator of the right-hand side in a Taylor series:

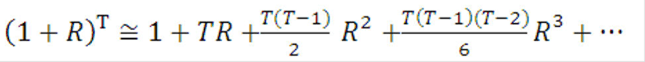
Description of formula to calculate the coupon rate follows

Therefore,

Description of formula to calculate the coupon rate follows

The user would then input the following formula coefficients:

and all other coefficients equal to zero. The following example shows that we do not need to go very far in the Taylor series to converge to the true value of the coupon rate. This is important to remember because a long formula necessitates more computing time than a slow one.

Term: T=0.5

Yield: R =0.05

Computation of Effective Duration and Effective Convexity

Oracle ALM does not directly output effective duration and effective convexity. However, a simple manual procedure computes delta and therefore effective duration and convexity. We describe this procedure hereafter.

8.     Create a Forecast Rates assumption rule with 3 scenarios:

Scenario 1: Flat Rates

Scenario 2: Shock Up 100 bps

Scenario 3: Shock Down 100 bps

9.     Run an Oracle ALM Deterministic Process to compute the market value for all 3 scenarios.

Scenario 1: MV0

Scenario 2: MV+

Scenario 3: MV-

10.  Effective Duration can be easily computed manually (for example, in ALMBI):

Description of formula to calculate the Effective Duration follows

11.  Effective Convexity can also be easily computed manually:

Description of formula to calculate the Effective Convexity follows

NOTE:   

A similar process can be defined using the Monte Carlo engine. With this approach, you must define additional Rate Management, valuation curve IRCs that reflect the immediate parallel rate shocks to the as-of-date rates. You must additionally map each of these IRCs into separate Stochastic Rate Index rules with each rule using one of the three IRCs as the valuation curve, as appropriate. Using these Stochastic Rate Indexing rules, the Monte Carlo engine must be run three times to produce the Market Values for each scenario: (Base, +100, -100). The resulting Option Adjusted Market Value results can be fed into the above formulas to arrive at Option Adjusted Duration and Option Adjusted Convexity.

References

1.     Black, F. Interest Rates as Options. Journal of Finance, 1995.

2.     Bratley, P., and Fox. Algorithm 659: Implementing Sobol's Quasirandom Sequence generator. ACM Transactions on Mathematical Software, 1988.

3.     Caflisch, R., Morokoff, and A. Owen. Valuation of Mortgage-Backed Securities Using Brownian Bridges to Reduce Effective Dimension. Caflisch' World Wide Web site, 1997.

4.     Chan, K.C., G.A. Karolyi, F.A. Longstaff, and A.B. Sanders. An Empirical Comparison of Alternative Models of the Short-Term Interest Rate. Journal of Finance, 1992.

5.     Fitton, P. Hybrid Low Discrepancy Sequences. Effective Path Reduction for Yield Curve Scenario Generation. To appear in the Journal of Fixed Income.

6.     Flesaker, B. Testing the Heath-Jarrow-Morton/ Ho-Lee Model of Interest Rate Contingent Claims Pricing. Journal of Financial and Quantitative Analysis, 1993.

7.     Ho, T.S.Y., and S.-B Lee. Term Structure Movements and Pricing Interest Rate Contingency Claims. Journal of Finance, 1986.

8.     Hull, J. Options, Futures, and Other Derivatives. Prentice-Hall, 1993.

9.     Hull, J. Options, Futures, and Other Derivatives. Prentice-Hall, 1997.

10.  Hull, J., and A. White. One-factor Interest-Rate Models and the Valuation of Interest-Rate Derivative Securities. Journal of Financial and Quantitative Analysis, 1993.

11.  Joy, C., Boyle, and Tan. Quasi-Monte Carlo Methods in Numerical Finance. Management Science, 1996.

12.  Lord, G., Paskov, Vanderhoof. Using Low-Discrepancy Points to Value Complex Financial Instruments. Contingencies, 1996.

13.  Morokoff, W., and R. Caflisch. Quasi-Random Sequences and Their Discrepancies. SIAM Journal of Scientific Computing, 1994.

14.  Niederreiter, H. Random Number Generation, and Quasi-Monte Carlo Methods. Regional Conference Series in Applied Mathematics, SIAM, 1992.

15.  Owen, A. Monte Carlo Variance of Scrambled Equidistribution Quadrature. SIAM Journal of Numerical Analysis, 1996.

16.  Press, W., S. Teukolski, W. Vetterling, B. Flannery. Numerical Recipes in C, The Art of Scientific Computing. Cambridge University Press, 1992.

17.  Spanier, J. private communication, 1997.

18.  Spanier, J., and Li. Quasi-Monte Carlo Methods for Integral Equations. Unpublished.

19.  Vasicek, O.A. An Equilibrium Characterization of the Term Structure. Journal of Financial Economics, 1977.