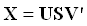行列操作

特異値分解(SVD)は、矩形行列Xを3つの行列(U、SおよびV)の積に分解する因数分解方法です。

図7-12 マトリックス操作

U行列は、「左」正規直交基底のセットから構成されます
S行列は、対角行列です
V行列は、「右」正規直交基底のセットから構成されます

Sの値は、特異値と呼ばれます。これらは、非負数で、それらの大きさは対応する基底(成分)の重要度を示します。特異値は、基底によって取得されたデータ分散の量を反映します。第1基底(最大の特異値を持つ基底)は、最大のデータ分散の方向に存在します。第2基底は、2番目の最大分散を持つ直交方向を取得します(以降同様に続きます)。

SVDは、基本的に、変換された軸をデータの最大分散の方向に揃える座標回転を実行します。これは、観測されるデータに高いS/N比が存在し、大きい分散が目的のデータ内容に対応し、小さい分散がノイズに対応するという仮定の下では有益な手順です。

SVDでは、基礎となるデータがガウス分布に従っており、平均と共分散の観点から適切に記述できると仮定します。