ドット積類似度

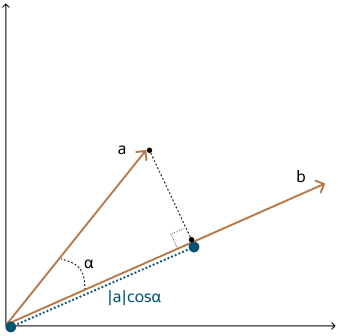
2つのベクトルのドット積の類似度は、各ベクトルのサイズに角度のコサインを掛けることと見なすことができます。この定義に対応する幾何学的解釈としては、1つのベクトルのサイズに、1番目のベクトルに対する2番目のベクトルの投影のサイズを乗算することと同等です。また、その逆も同様です。

次の図に示すように、一方のベクトルをもう一方のベクトルに投影し、結果のベクトル・サイズを乗算します。

ところで、これは各ベクトルの座標の積の合計に相当します。多くの場合、2つのベクトルの角度のコサインにアクセスできないため、この計算のほうが簡単です。

ドット積の値が大きいほどベクトルが類似していることを示し、値が小さいほど類似していないことを示します。ユークリッド距離の使用と比較して、ドット積類似度の使用は高次元ベクトルに特に有用です。

ベクトルの正規化およびドット積類似度の使用は、コサイン類似度の使用と同等であることに注意してください。ドット積類似度がコサイン類似度よりも速く評価される場合と逆にコサイン類似度がドット積類似度よりも速い場合があります。正規化されたベクトルは、正規化されたベクトルのノルムが1になるように、各次元をベクトルのノルム(または長さ)で除算することによって作成されます。

図dot_product_similarity2.epsの説明