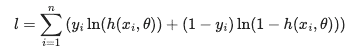GWR分類子
Geographically Weighted Regression (GWR)分類子は、空間異種性の存在下で使用されるバイナリ分類子で、リージョン変動の兆候として識別できます。
このアルゴリズムは、近傍内の観測からターゲット変数と説明変数を組み込むことによって、データセット内のすべての観測に対してローカル分類子を作成し、独立変数と依存変数の間の関係を近傍性によって変えることができます。
分類子は、データセット内のすべてのサンプルのロジスティック回帰モデルをトレーニングし、指定された帯域幅内に収まるロケーションの依存変数および独立変数を組み込みます。 目的は、次のように定義されたクロス・エントロピ損失関数を最大化することです。
前述の関数で、yは0または1で、関数hはSigmoid関数であるロジスティック回帰のアクティブ化関数です。
次の表に、GWRClassifierクラスの主なメソッドを示します。
| メソッド | 説明 |
|---|---|
fit |
アルゴリズムには帯域幅が必要です。この帯域幅は、ユーザーがbandwidthパラメータを使用するか、spatial_weights_definitionパラメータを指定して設定できます。
|
predict |
予測を行うために、GWRでは、トレーニング・データからの隣接する観測値を使用して、予測セットの各観測のモデルをトレーニングします。 次に、これらのモデルを使用してターゲット変数を見積もります。 |
fit_predict |
トレーニング・データを使用して、fitおよびpredictメソッドを順番にコールします。
|
score |
指定されたデータのモデルの精度を返します。 |
詳細は、「Oracle Spatial AI Python APIリファレンス」のGWRClassifierクラスを参照してください。
次の例では、block_groups SpatialDataFrameを使用して次のステップを実行します:
- ターゲット変数として使用する
MEDIAN_INCOME列に基づいて、カテゴリ変数を作成します。 GWRClassifierのインスタンスを作成します。- トレーニング・セットを使用してモデルをトレーニングします。
- トレーニング済モデルを使用して、モデルからの予測およびモデルの精度を出力します。
import pandas as pd
from oraclesai.preprocessing import spatial_train_test_split
from oraclesai.weights import DistanceBandWeightsDefinition
from oraclesai.classification import GWRClassifier
from oraclesai.pipeline import SpatialPipeline
from sklearn.preprocessing import StandardScaler
# Create a categorical variable, "INCOME_LABEL", based on the second quantile of the median income
block_groups_extended = block_groups.add_column("INCOME_LABEL", pd.qcut(block_groups['MEDIAN_INCOME'].values, [0, 0.5, 1], labels=[0, 1]).to_list())
# Set a referenced coordinate system
block_groups_extended = block_groups_extended.to_crs('epsg:3857')
# Define the target and explanatory variables
X = block_groups_extended[['INCOME_LABEL', 'MEAN_AGE', 'MEAN_EDUCATION_LEVEL', 'HOUSE_VALUE', 'INTERNET', 'geometry']]
# Define the training and test sets
X_train, X_test, _, _, _, _ = spatial_train_test_split(X, y="median_income", test_size=0.2, random_state=32)
# Define the spatial weights definition
weights_definition = DistanceBandWeightsDefinition(threshold=15000)
# Create an instance of GWRClassifier
gwr_classifier = GWRClassifier(spatial_weights_definition=weights_definition)
# Add the model to a spatial pipeline along with a pre-processing step
classifier_pipeline = SpatialPipeline([('scale', StandardScaler()), ('gwr', gwr_classifier)])
# Train the model specifying the target variable
classifier_pipeline.fit(X_train, "INCOME_LABEL")
# Print the predictions with the test set
gwr_predictions_test = classifier_pipeline.predict(X_test.drop("INCOME_LABEL")).flatten()
print(f"\n>> predictions (X_test):\n {gwr_predictions_test[:10]}")
# Print the accuracy with the test set
gwr_accuracy_test = classifier_pipeline.score(X_test, "INCOME_LABEL")
print(f"\n>> accuracy (X_test):\n {gwr_accuracy_test}")出力は、最初の10個の観測の予測と、テスト・セットを使用したモデルの精度で構成されます。
>> predictions (X_test):
[1 1 0 0 1 0 1 0 0 0]
>> accuracy (X_test):
0.8384279475982532summaryプロパティには、グローバル・ロジスティック回帰の統計とGWRClassifierが含まれます。 推定パラメータについては、すべてのローカル・モデルの平均値が表示されます。
===========================================================================
Model type Binomial
Number of observations: 2750
Number of covariates: 5
Global Regression Results
---------------------------------------------------------------------------
Deviance: 2088.938
Log-likelihood: -1044.469
AIC: 2098.938
AICc: 2098.960
BIC: -19649.694
Percent deviance explained: 0.452
Adj. percent deviance explained: 0.451
Variable Est. SE t(Est/SE) p-value
------------------------------- ---------- ---------- ---------- ----------
X0 -0.044 0.061 -0.717 0.473
X1 0.439 0.072 6.084 0.000
X2 0.685 0.104 6.603 0.000
X3 0.542 0.109 4.989 0.000
X4 1.298 0.092 14.088 0.000
Geographically Weighted Regression (GWR) Results
---------------------------------------------------------------------------
Spatial kernel: Fixed bisquare
Bandwidth used: 15000.000
Diagnostic information
---------------------------------------------------------------------------
Effective number of parameters (trace(S)): 56.675
Degree of freedom (n - trace(S)): 2693.325
Log-likelihood: -888.994
AIC: 1891.337
AICc: 1893.765
BIC: 2226.816
Percent deviance explained: 0.534
Adjusted percent deviance explained: 0.524
Adj. alpha (95%): 0.004
Adj. critical t value (95%): 2.850
Summary Statistics For GWR Parameter Estimates
---------------------------------------------------------------------------
Variable Mean STD Min Median Max
-------------------- ---------- ---------- ---------- ---------- ----------
X0 -0.020 0.846 -1.630 -0.140 3.328
X1 0.512 0.325 0.020 0.385 2.156
X2 0.931 0.665 -1.213 1.168 2.893
X3 0.995 0.981 -0.615 0.834 6.249
X4 1.190 0.356 0.324 1.119 2.531
===========================================================================