Az Automatikus helyzetképek által létrehozott ábrázolástípusok
Az Automatikus helyzetképek többféle típusú ábrázolást generálnak, amelyek specifikus helyzetképeket biztosítanak az adatokról. Ezen ábrázolások mindegyike az adatok különböző oszlopait használja, és a helyzetkép értékétől függően kerül rendszerezésre az adatok kontextusában.
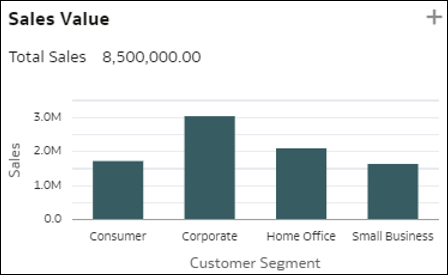
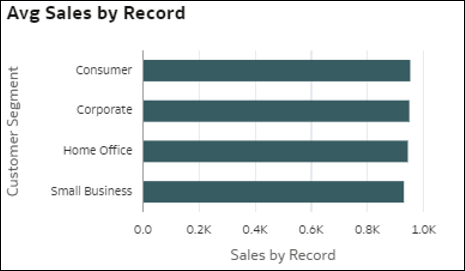
- Dimenzióbontások – Ezek az ábrázolások összesítenek egy, az adatok egy dimenziójának különféle tagjaihoz kapcsolódó mérőszámértéket. Így gyorsan áttekintheti a kiválasztott mérőszám eloszlását egy adott dimenzióhoz képest. Ez a mérőszám lehet az adatkészlet egyik mérőszáma, rekordok száma, vagy a mérőszám rekordonkénti átlagos értéke.
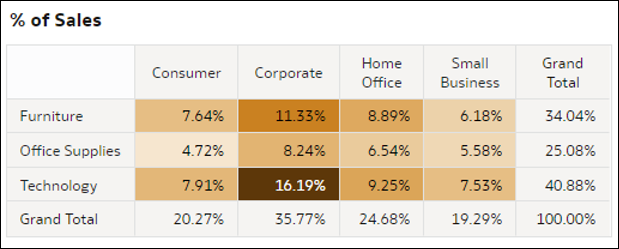
- Hőtérképes kimutatástáblák – Ezek az ábrázolások összesítenek egy mérőszámot az adatok két dimenziójának metszéspontjaiból. A kimutatástábla minden cellája a két kiválasztott D2 dimenzió tagjainak metszéspontját jelöli. Az ilyen ábrázolások segítségével gyorsan átláthatja, melyek a mérőszám legmagasabb értékei - ehhez csak keresse meg a táblák legsötétebb celláit. Ebben az ábrázolásban a mérőszámok lehetnek az adatkészletből származó egyik mérőszám, rekordok száma, egy mérőszám rekordonkénti átlagértéke, vagy egy ezen lehetőségek bármelyikét képviselő százalék (a jobb felső sarokban lévő összegzés értéke 100%).
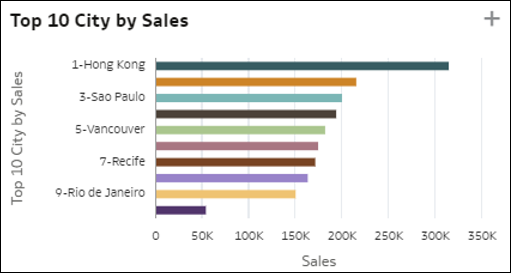
- Top 10 tag – Ez az ábrázolás az adatkészlet egy dimenziójának legfőbb tagjait jeleníti meg egy mérőszámhoz kapcsolódóan, értékük szerint csökkenve. A diagram utolsó sávjában az összes olyan tag mérőszámának átlagértéke látható, amelyek nincsenek a legfelső kilencben. Ez az M1 átlagértéke az összes olyan tag esetében, amelyek nincsenek a legfelsők között. Ez az információ megjeleníti, hogy a legfelső tagok mennyire vannak a populáció többi tagjának átlaga fölött.
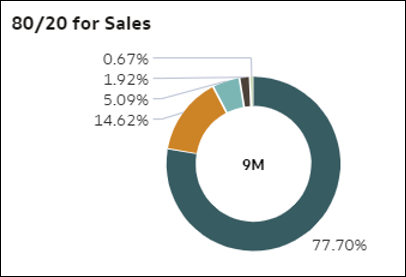
- 80/20 – Ez az ábrázolás egy adott mérőszám esetében megmutatja, hogy az adatok legfelső 20%-ában lévő rekordok a teljes adatkészletből mennyit tesznek ki. A top 20%-ot a program az adatkészlet részletes oszlopai alapján számítja ki. A fánkdiagram megmutatja, mennyire fontosak a legfelső tagok az adatok adott mérőszáma szempontjából. A fánkdiagram ívei a rekordok kvintiliseit jelölik, azaz a rekordok egymást követő 20%-os tömbjeit a sorok csökkenő száma alapján (tagok legfelső 20%-a, aztán a következő 20% és így tovább). Az ívek mérete az adott mérőszám kvintilisre vonatkozó teljes összesített értékét jelöli.
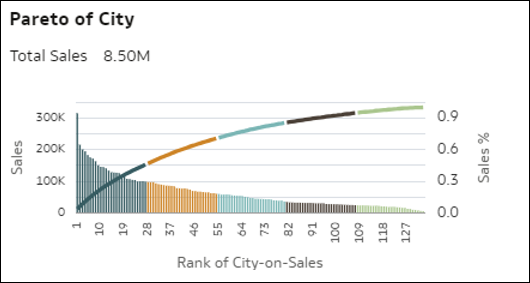
- Pareto-diagram – A Pareto-diagram ábrázolásán látható a dimenzió összes tagja (közepes kardinalitás) egy mérőszám értéke szerint csökkenő sorrendbe állítva. Minden sáv ezt a mérőszámot képviseli az egyes tagokra vonatkozóan, míg a vonal a mérőszámérték halmozott százalékát jelöli (összesen 1,0 =100%), mivel a dimenzió minden egyes tagja halmozottan kerül hozzáadásra. A Pareto-diagram segítségével kiemelhetők azok a területek, amelyek a legnagyobb relatív értéket vagy gyakoriságot képviselik.
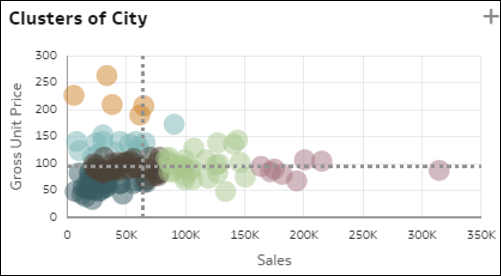
- Szórásdiagramok és klaszterek – A szórásdiagram diagramábrázolás a dimenzió összes tagját megjeleníti (közepes kardinalitás) egy rácson. A tengelyeken az adatokból származó két egyedi mérőszám szerepel. A mérőszámok beosztása átlagos egységérték alapján történik. A rekordok közötti szórás és a potenciális kiugró értékek érdekes helyzetképeket adnak a dimenzióelemekről. Ezzel a diagrammal gyorsan áttekinthető, hogy a két mérőszám a B1 tagokon mennyire korrelál jól egymással, és a segítségével egyszerűen megértheti, hogy melyik tag melyik kvadránsba tartozik. A szórásdiagramok egyik változatán a rekordok hat koherens csoportba vannak klaszterezve automatikusan.
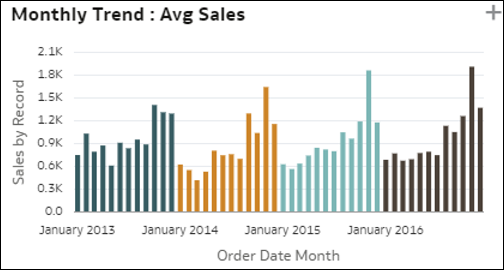
- Egyszerű sávdiagram trendekkel – Ez az ábrázolás egy mérőszám trend szerinti fejlődését mutatja az adatkészlet egyik időoszlopával összevetve. Érdekes trendmintákat vehetünk észre rajta, például növekedést vagy csökkenést. Ez a mérőszám lehet az adatkészlet egyik mérőszáma, rekordok száma, vagy egy mérőszám rekordonkénti átlagos értéke. Ugyanez a helyzetkép megjelenhet egy további előrejelzési vonallal a diagram jobb oldalán.
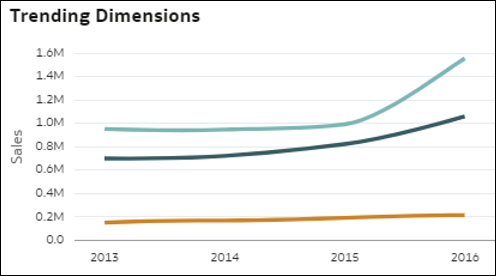
- Összehasonlító trend dimenzió alapján – Ez az ábrázolás összehasonlítja egy mérőszámérték trendjét az adatok egyik dimenziójának minden egyes tagjánál. A diagram minden vonala egy mérőszám változását mutatja a dimenzió egy adott tagjánál. A mérőszámérték növekedése vagy csökkenése nem feltétlenül konzisztens a dimenzió összes tagjánál, ami érdekes helyzetképhez vezethet: Melyik tag trendje különbözik a többiétől?
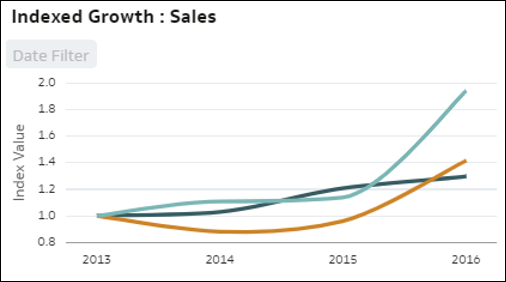
- Összehasonlító indexelt trend – Ez az ábrázolás összehasonlítja egy mérőszám relatív növekedését az idő során az adatai egyik dimenzióoszlopának minden tagjánál. Minden vonal a dimenzió egyik tagját jelöli, a kezdeti időszakban az alap indexérték 1,00. Az idő során történő változás a következő időszakok relatív értékét jeleníti meg a kezdeti időszak indexértékével (1,00) összehasonlítva. Azzal, hogy abszolút értékek helyett indexelést használ, megfelelően össze tud hasonlítani különféle trendeket, mert a vonalak a valódi relatív fejlődést tükrözik, megfelelően összehasonlítva a tagok növekedését a többihez képest. Ha az indexelt értékek helyett a mérőszámok abszolút értékeit nézzük, az értékek eltérései miatt gyakran lehetetlen megfelelően összehasonlítani a növekedést vagy a csökkenést. Az indexek használata segít megérteni a tényleges relatív viselkedést.
- Indexelt trendek mérőszámok alapján – Ez az ábrázolás az adatkészlet több tagjának relatív fejlődését hasonlítja össze az idő folyamán. A vonaldiagram az adatkészlet különböző mérőszámainak indexelt értékét ábrázolja az idő folyamán. Minden vonal egy mérőszámot képvisel. Azzal, hogy abszolút értékek helyett indexelést használ, megfelelően össze tud hasonlítani különféle trendeket, mert ha a mérőszámok abszolút értékeit nézzük, akkor gyakran lehetetlen megfelelően összehasonlítani a növekedést vagy a csökkenést. A kezdő indexérték (1,00) a kezdeti időszakban minden mérőszámra beállításra kerül, és a vonalon az egyes mérőszámok relatív fejlődése látható a diagramon szereplő kiindulási pontjához (index) képest.
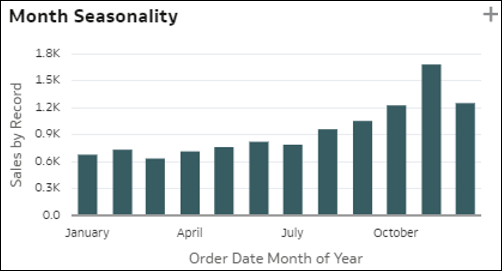
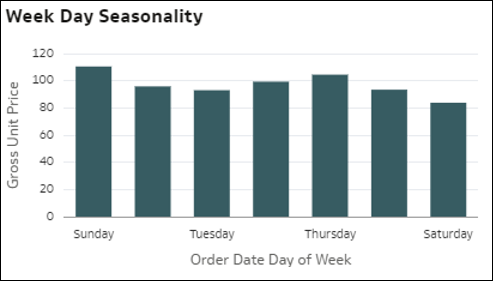
- Szezonalitások – Az ábrázolás sávjai egy mérőszám eloszlását jelölik Év hónapja, Hónap napja vagy Hét napja szerint, az adatkészlet egyik időobjektuma alapján. Ebből kikövetkeztethető az arányérték potenciális szezonalitása a hónapok során. A szezonalitás diagramok jól jönnek, ha ismétlődő mintákat szeretnénk azonosítani az adatokban, adott időszakok során. Ez fontos lehet annak megértéséhez, hogy a mérőszámértékek hogyan változnak szezonálisan.
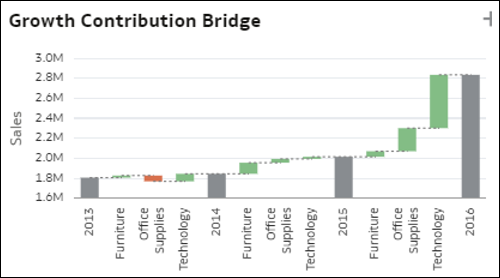
- Tagi hozzájárulás híddiagramja – Ezen a híddiagramon az adatkészlet egyik dimenziójának összes tagjának hozzájárulása látható egy mérőszámérték variációjához az idő folyamán. A segítségével megérthetjük, hogy mely tagok járultak hozzá leginkább egy variációhoz egy időszakban (növekedés vagy csökkenés tekintetében). A diagram minden szürke sávja egy mérőszám teljes értékét jelöli egy T1 időszakban. A két időszak közötti zöld vagy piros sávok azt jelölik, hogy mely tagok növekedtek vagy csökkentek, és ezáltal hogyan járultak hozzá a teljes variációhoz.
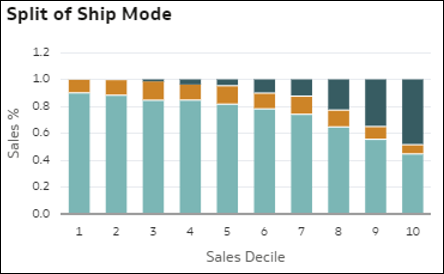
- Dimenzióelemek felosztása (kevert) a Mérőszámértékkel szemben – Ez az ábrázolás segít megérteni az adatok egyik dimenziója összes tagjának a keveredését (felosztását), ahogy növekszik egy mérőszám értéke. A sávok a mérőszám relatív értékét jelölik: 1. decilis = alacsony mérőszámérték rekord szerint (a rekordok első 10%-a), 2. decilis = második 10%, egészen a 10. decilisig = magas mérőszámérték rekord szerint. Az egyes sávokban a színek jelölik a dimenzió egyes tagjainak arányát (a teljes százaléka) a mérőszám teljes értékéhez képest, az adott decilisnél. Ez segít azonosítani, hogy a tagok keverékének struktúrája változik, ahogy a mérőszámérték is változik.
- Egy mérőszám hisztogramja rekordtárolók szerint – Ez az ábrázolást egy mérőszám eloszlását mutatja egy másik mérőszám tárolói szerint. A diagram sávjai a mérőszám összesítését mutatják; minden sáv a mérőszám egy tárolóját jelöli: 1. tároló = alacsony mérőszámérték rekord szerint, 10. tároló = magas mérőszámérték rekord szerint.
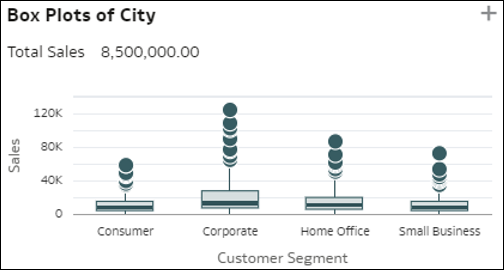
- Dimenzióelemek dobozdiagramja – Ez a dobozdiagram-ábrázolás összehasonlítja a tagok eloszlását az adatok (pontok) D1 dimenziójában (közepes kardinalitás) az adatokban szereplő mérőszám értékével. Az adatok másik dimenziójának (D2) egyes tagjai szerint van ábrázolva (sávok). A dobozdiagram minden egyes sávja a D2 egy tagját képviseli, míg a sávban lévő minden egyes pont egy D1-tag. Az Y tengelyen az utóbbi mérőszámának átlagos egységértéke látható. Minden sáv egy D2-tag három értékét jelöli: az első kvartilis értékét a sáv alján, az átlagértéket a sáv közepén, illetve a harmadik kvartilist fent. Ennek az ábrázolásnak a segítségével egyszerűbb megérteni a rekordok eloszlását a D1 dimenzióban, és összehasonlítani az eloszlásban jelentkező különbségeket a D2 dimenzió tagjaival.
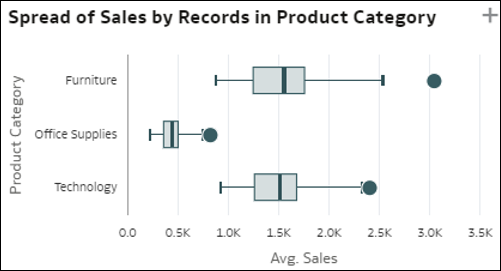
- Rekordértékek eloszlása dimenzió alapján – Ez a diagramábrázolás jelöli egy mérőszámérték rekordjainak szóródását (szórás) egy adott dimenzió minden egyes tagjánál (sávok). Az X tengelyen a mérőszám átlagos értéke látható rekord szerint. A sávokban szereplő pontok részletes rekordok véletlenszerű csoportjait jelölik az adatkészletből. Ez az ábrázolás segít annak a megértésében, hogy a szórás hogyan változhat egy dimenzió különböző tagjai között (az ábrázolás különböző vízszintes sávjai).
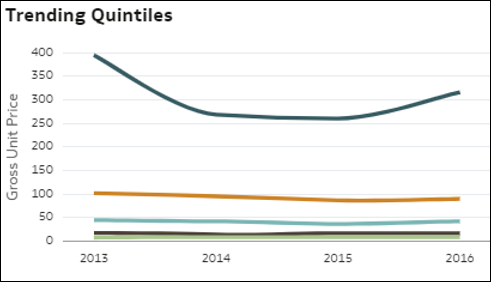
- Kvintilisek trendjeinek összehasonlítása – Ez az ábrázolás összehasonlítja, hogy az adatok rekordjainak 20%-os csoportjai (egy mérőszám értéke szerint rendszerezve) a legfelsőktől a legalsókig (kvintilisek) milyen trendek részét képezték az idő folyamán, a saját mérőszámértékük vonatkozásában. A növekedés vagy csökkenés konzisztens volt a legfelső és legalsó csoportokban vagy sem? Melyik populációcsoportnál tér el a mérőszám trendje? A diagram minden egyes vonala egy kvintilis amely az M1 érték trendjét mutatja. A kvintilisek az adatkészlet rekordjainak 20%-onként felosztott csoportjai, amelyek csökkenő mérőszámérték alapján vannak sorba rendezve: a legfelső 20% értékkel rendelkező rekordok, amelyeket a következő 20% követ, és így tovább.