State estimation utilizes a Weight Least Squares algorithm. This is a non-linear least squares solver. We build up a system of equations that fall into one of 3 types:

The goal of state estimation is to find a “best estimate” of nodal voltages: Vi that minimizes a weighted least squares equation constructed from those 3 different residual equations above. Assume we have M measurements for N nodes. Each specific measurement (for a device and measurement type) has a computable estimate: Est(V) that depends on the state of the network (that is voltages at multiple nodes). For given set of voltages V, we can compute the (complex) power in each individual branch: Sbr(V). Taken together we seek to minimize a function f(V) that is defined by:

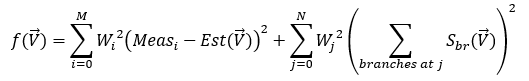
Est(V) is one of the following functions: Voltage, Angle, Current, Real Power, or Reactive Power. The computation of it changes by each type. The individual weights have a large impact on results. Each measurement can define its own weight. We define weight in terms of expected measurement errors (variance/standard deviation). These are computed assuming two independent forms of error: Relative Error and Absolute Error as follows:

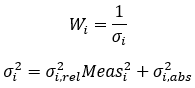
Which allows small measurements to be just as important as large measurements (note Meas used here is a per-unit measurement, and if σ is zero we disable the measurement). For the power injection equations, we use this same format, for any node with loads we use globally configured pseudo-measurement weights and for any other nodes we just take a measurement of 0 and let the absolute error dominate. We want the zero-injection weight to be as large as possible so that those equations get enforced. We normalize all weights by the largest weight for stability (but all user facing weights remain unnormalized). We can recast the above equation into a single summation:

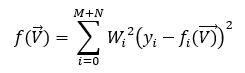
Which is in the standard form of a non-linear least squares. We solve this via iteratively reweighted least squares with Levenberg-Marquardt (damped least squares), meaning the non-linear solver can reweight residuals to reduce the impact of outliers, these are applied on top of the configured weights.