This section provides an overview of batch architecture included in Oracle Utilities Cloud Services. It is intended solely to help you assess the business benefits of the batch processing architecture.

Oracle Utilities Cloud Services include mature and robust batch processing features to achieve the following goals:

It has long been the case when batch jobs are submitted that a thread count parameter is specified to tell the batch runtime the number of chunks that the job's work should be split into for parallel execution. We refer to these chunks "threads of work". That is, the thread count describes the number of threads of work for a job. Each thread of work is then assigned by the system to run on a single thread of system capacity whenever sufficient capacity exists. We refer to these units of system capacity "threads of capacity". In summary, the thread count on a job specifies the number of threads of work that the job will be split into and then based on the current usage and capacity of the environment those threads of work are matched to threads of capacity at which point work is performed. Those same concepts have been extended to substantially improve the efficiency and overall experience of running batch jobs in Software-as-a-Service (SaaS). The remainder of this section provides details.

It is common practice today for jobs to be submitted with the expectation that immediately after submission each thread of work is matched to a free thread of capacity, the threads run for some time and then after the last thread completes then the job is completed. Consider the diagram below which illustrates the coarse-grained submission of two jobs ("Job 1" and "Job 2") followed by descriptions of common difficulties associated with this type of submission.

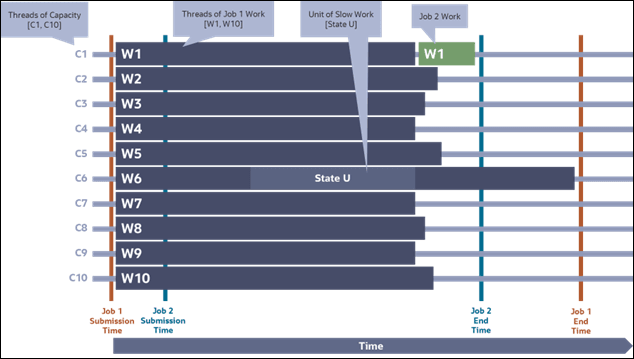
Figure 3-1: Coarse-Grained Submission - Two Jobs

In this example, Job 1 is submitted with a thread count of 10. Notably, thread #6 of Job 1 contains a unit of work labeled "State U" representing some unit of work requiring far more time to complete than other units. The name is chosen in reference to accounts often related to universities which can be particularly complex. Correspondingly, this complex unit of work causes thread #6 to finish at a time much later than the other threads and hence the completion time of the overall job is delayed while waiting for that single thread. Any jobs depending on the completion of Job 1 are likewise delayed.

Similar difficulties although usually of a lower typical impact arise because a particular thread of capacity runs on a computer suffering greater resource contention (eg. network, CPU) than other computers and therefore the thread of work finishes later than others which causes the overall job to finish later.

The root of the difficulty is that each thread of work has committed itself to run on a single thread of capacity throughout the duration of the job. Hence no rebalancing of the workload is possible once the job starts.

Consider Job 2 in the diagram which was submitted a short time after Job 1 was submitted. Despite Job 2 having only one thread of work and running comparatively quickly, Job 2 is blocked from running for a long time. Only when a thread of Job 1 completes can Job 2 run at all. This is an example of the well-known challenge in task processing systems, the problem of "resource starvation."

Consider Figure 3-2 in which an already running job (Job 0) is utilizing one thread of capacity when the parallel job (Job 1) is submitted. Because the single thread (W1) of Job 0 makes one thread of capacity unavailable the result is that the overall completion of job 1 is delayed for the full duration of this capacity shortfall. Coarse-grained job submissions are often incapable of handling thread capacity shortfalls without delays to job completion time.

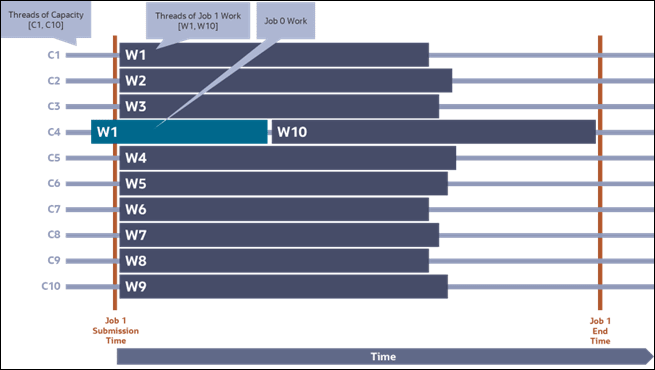
Figure 3-2: Coarse-Grained Submission - Delayed Job Completion

To avoid difficulties #2 and #3 and to make possible the scheduling of other types of jobs along with parallel jobs like Job 1 it is common to lower the thread count of jobs like Job 1 such that spare capacity is maintained. However, as Figure 3-3 below demonstrates this leads to unused capacity which might otherwise be used to lower the completion time of Job 1.

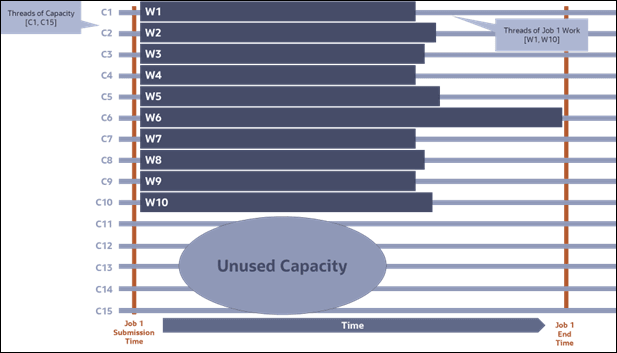
Figure 3-3: Coarse-Grained Submission - Unused Capacity

The remainder of this section describes how difficulties #1 - #4 are solved through Fine-Grained Thread Submission.

Technical features implemented in Oracle Utilities Cloud Services make possible the submission of jobs with much higher thread counts as well as more sophisticated policies governing how pending threads of work are matched to free threads of capacity. By higher thread counts we mean that a job may be submitted specifying far more threads of work than the number of threads of capacity available in the system. And since most of these threads of work cannot run immediately a queue of pending threads of work forms as do queues of pending work corresponding to other jobs similarly submitted. Having queued substantial threads of work, the system can employ concepts and algorithms of queue theory to solve the difficulties previously discussed:

Let us get started by reimagining Job 1 being submitted with 10x more threads of work than described in the coarse-grained submission discussion. Instead of Figure 3-1 we would expect the following scheduling behavior:

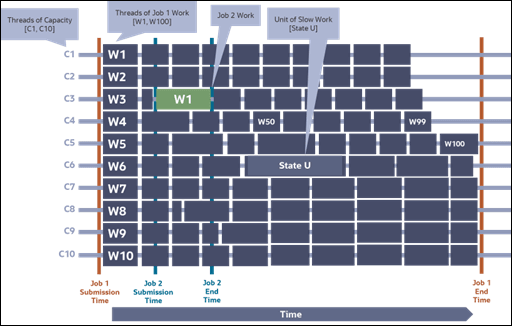
Figure 3-4: Fine-Grained Submission

Note in Figure 3-4 that Job 1's overall completion time is considerably shorter than in Figure 1. While the "State U" slow unit of work is still slow, its effect on overall completion time is mitigated by the fact that the thread of capacity ("C6") on which the slow work is scheduled performs fewer threads of work than other threads. For example, while thread of capacity C6 completes 6 threads of work, thread of capacity C7 performs 11 threads of work. In essence, the well-behaved workflows around the poorly behaving work. Threads of capacity capable of performing more work receive more work to do while threads of capacity unable to complete work quickly are assigned less work. This behavior is the essence of what is known as "queue-based load leveling".

Note that is possible to construct scenarios where problematic work like "State U" happens to fall among the last threads of work scheduled (e.g. W100). However, it can be shown via statistical means that under most situations the queue-based load leveling shown here has far superior results than displayed by the coarse-grained thread scheduling.

Note in Figure 3-4 that Job 2 starts processing and completes much sooner than in Figure 3-1. That is, we do not see Job 2 exhibiting resource starvation. This owes to two reasons:

Please consider Figure 3-5 and note that unlike Figure 3-2 that a thread of work from another job (Job 0) does not unreasonably extend the completion time for the newly scheduled Job 1. Rather, queue-based load leveling causes the impacted thread of capacity (C4) to preform less work (6 threads of work) relative to the other threads of capacity which process as many as 13 threads of work.

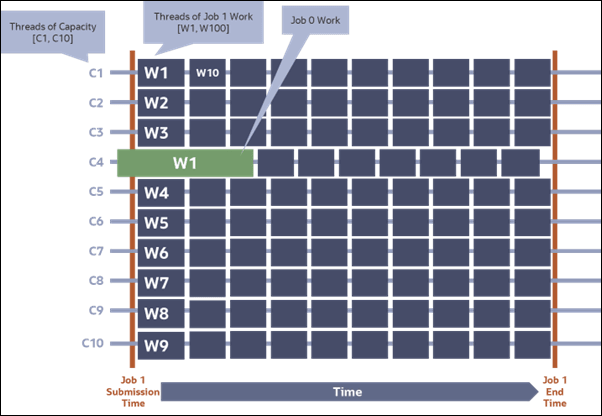
Figure 3-5: Fine-Grained Submission - Previously Running Job

It should be clear that the same property of queue-based load leveling which enables a job to handle shortfalls of thread capacity can also utilize excess capacity to further shorten completion job times. This is shown in Figure 3-6. When additional capacity is available it can be used to lower job completion times and if jobs are scheduled which require that additional capacity then the fair task queueing feature will ensure that those jobs receive threads of capacity according to the business-value optimizing policies defined through configuration.

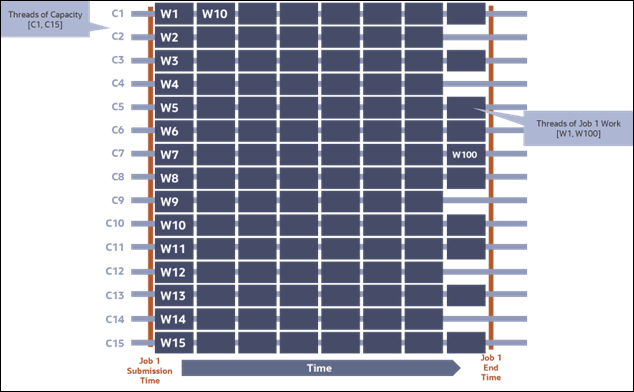
Figure 3-6: Fine-Grained Submission - Excess Capacity Shortens Completion Times

As described earlier, queue-based load leveling deals well with some threads of work having longer durations than the typical threads of work within a job. Nonetheless, there should be some well-defined maximum expected duration for typical threads of work. It also follows that this maximum thread duration should be targeted to be under 2 minutes. This prevents many threads of work from consuming threads of capacity for long durations and thus defeating the dynamic load balancing and fairness-based thread scheduling already been discussed. Thus, the recommendation offered here is to attempt to adjust the thread count of jobs such that the great majority of threads of work will finish in under two minutes.

Based on analysis of subscribers' batch processing within the cloud services the typical customer would need to increase their thread counts approximately 10x for 10-20 batch controls. The actual thread count achieving under-two-minute runtimes is expected to range somewhere between 200 and 1,000 threads of work. In general, only these 10-20 batch controls would need to be adjusted since all other jobs already complete in under 2 minutes or are single-threaded jobs. However, a very small number (one or two, typically) may need to have their thread counts increased by 40-100x, the "D1-IMD" batch control being a candidate for such an increase in thread count.

As already described, batch processing functionality has been enhanced such that jobs can be submitting with high thread counts which leads to many threads of work being initially queued by the system. Further, the system achieves business objectives like minimizing job completion times, maximizing resource utilization, and preventing resource starvation by optimally deciding which job to dequeue threads of pending work when multiple jobs have queued work. The common term denoting optimal choices like these is "fairness" and we will refer to the key objective in this context as "fair task scheduling". This section will describe the cloud service's implementation of fair task scheduling and the ways that administrators can influence scheduling decisions to optimize business objectives.

Much queueing theory originates from research into optimizing packet-switched networks and the terminology generally follows from that field. One term that we will use here is that of the "flow" which means a collection of backlogged work items that might be scheduled. A simple example of flows is where two batch jobs are submitted concurrently such that pending threads of work are queued for both jobs. In this case, each queue constitutes a flow, and the batch runtime must optimally choose to schedule threads of work for one flow versus the other.

The criteria for choosing one flow versus another is made based on tracking of the amount of "service" provided to each flow in the recent past. A flow that received less weighted service will be scheduled before another flow that has received more service. We will defer discussing the term "weighted" mentioned just now until the term "service" is better defined. ervice is a scalar value representing the accumulated time that threads of work executed on threads of capacity. For example, if one thread of work executed for 30 seconds before completing then the flow that the work belongs would see its tally of service received increase by a value of 30. Likewise, if 5 threads from one flow each executed for 30 seconds then that flow's service received value would increase by 150. Note that a thread of work does not need to complete for the service provided to be accumulated and therefore factor into scheduling decisions. Service quantities are incrementally applied to flows' tallies as threads of work run.

Consider Figure 3-7 below which shows that among two flows, batch jobs running batch controls DEFAULT1 and DEFAULT2, that a free thread of capacity is scheduled work from the flow having the lowest value of service received (100 vs. 101.5).

Figure 3-7: Two Flows

After some time, another thread of capacity becomes available to execute a thread of work. However, since work W1-1 from flow DEFAULT1 has been executing for some time, now flow DEFAULT2 has a lower value of service received. Therefore, work from flow DEFAULT2 is scheduled. Over time, each flow will receive approximately the same service because scheduling is performed from the flow having the lowest value of service received.

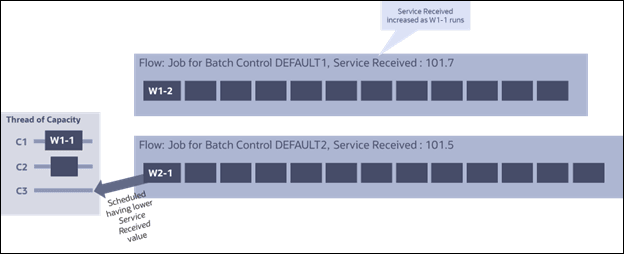
Figure 3-8: Two Flows - More Thread Capacity

Oracle Utilities Cloud Services enable extension of batch behavior by configuring Batch Resource Configuration extendable lookup values. One extendable lookup value should be specified for each Batch Control requiring non-default resource behavior. Specifically, a Resource Group value can be specified for each extendable lookup value and these Resource Group values serve two purposes in relation to fair queuing of batch work:

The following table lists the delivered Resource Group values and their weights.

The idea that scheduling takes place via nested flows is commonly referred to as "hierarchical fair scheduling" and there are many examples of such algorithms in computation. In this case we define a two-level hierarchy where the higher level is represented by the resource group and the lower level by the individual jobs. Thus, scheduling of a thread of work to a thread of capacity occurs in two steps:

Consider the following diagram showing three jobs competing for their backlogged threads of work to be scheduled. These jobs are of two different resource groups.

Figure 3-9: Three Jobs Competing for Backlogged Threads

Note in the example that the value of service received for the Priority 20 (Medium) resource group is 202 while the value of service received by the job of batch control MED1 is 808. This is because the resource group flow increases its value of service received inversely proportional to its weight. In this case, the higher-level flow's value is 202 = 808 / 4 where 4 is the weight of the resource group. Thus, this resource group will receive four times the service over time relative to the Default resource group that has a weight of one.

The following figure (3-10) conveys how the three jobs might receive service over time assuming that the environment is entitled to 60 threads of capacity.

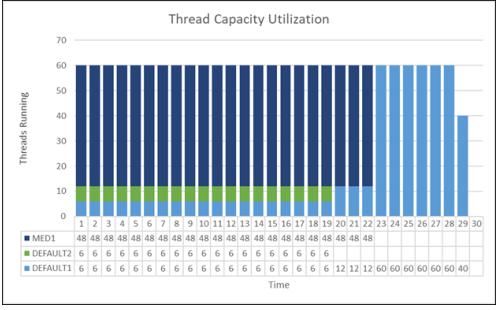
Figure 3-10: Thread Capacity Utilization

The examples provided are idealizations of system behavior. However, actual results may deviate somewhat from what users might view as perfect fairness for various reasons. For example, because the history of service provided to a flow is used to make future scheduling systems there can be some system dynamical effects where the behavior is either over-damped or under-damped based on the composition and timing of jobs submitted over time. However, the system will converge to a state of approximate fairness over a reasonable timeframe.

The hierarchical fair queueing algorithm described falls within the broad class of "non-preemptive work-conserving" scheduling algorithms. "Non-preemptive" means that once a thread of work is scheduled to a thread of capacity, the work will be allowed to complete even if higher priority work becomes queued and therefore cannot be immediately scheduled because of lack of free capacity. "Work-conserving" means that backlogged work will always be scheduled when free capacity exists. The combination of these choices promotes non-disruption of running processes and high resource utilization. However, the drawback is that submitting many threads of work where each thread takes a long time to complete might temporarily defeat the fair queueing algorithm by occupying most or all the thread capacity and therefore block the fair scheduling of subsequently submitted jobs.

The typical solution to the problem is to implement the fine-grained thread submission techniques already describe with particular attention to ensuring that most threads of work take no more than two minutes to complete. Thus, threads of work vacate threads of capacity often enough that overall scheduling fairness can be maintained by scheduling threads of work from under-served jobs onto the freed capacity. It is acknowledged that it may be impractically to split some jobs, like file extracts, into many threads. However, in those cases leaving these extracts to run single-threaded or via a small number of threads is acceptable since these threads of work will only occupy a minority of threads of capacity at the same time and overall system fairness can be maintained by scheduling work onto the remaining capacity.