| Sun Performance Library User's Guide
|
   
|
Using Sun Performance Library Signal Processing Routines
|
The discrete Fourier transform (DFT) has always been an important analytical tool in many areas in science and engineering. However, it was not until the development of the fast Fourier transform (FFT) that the DFT became widely used. This is because the DFT requires O(N2) computations, while the FFT only requires O(Nlog2N) operations.
Sun Performance Library contains a set of routines that computes the FFT, related FFT operations, such as convolution and correlation, and trigonometric transforms.
This chapter is divided into the following three sections.
- Forward and Inverse FFT Routines
- Sine and Cosine Transforms
- Convolution and Correlation
Each section includes examples that show how the routines might be used.
For information on the Fortran 95 and C interfaces and types of arguments used in each routine, see the section 3P man pages for the individual routines. For example, to display the man page for the SFFTC routine, type man -s 3P sfftc. Routine names must be lowercase. For an overview of the FFT routines, type man -s 3P fft.
Forward and Inverse FFT Routines
TABLE 6-1 lists the names of the FFT routines and their calling sequence. Double precision routine names are in square brackets. See the individual man pages for detailed information on the data type and size of the arguments.
TABLE 6-1 FFT Routines and Their Arguments
|
Routine Name
|
Arguments
|
|
Linear Routines
|
|
CFFTS [ZFFTD]
|
(OPT, N1, SCALE, X, Y, TRIGS, IFAC, WORK, LWORK, ERR)
|
|
SFFTC [DFFTZ]
|
(OPT, N1, SCALE, X, Y, TRIGS, IFAC, WORK, LWORK, ERR)
|
|
CFFTSM [ZFFTDM]
|
(OPT, N1, N2, SCALE, X, LDX1, Y, LDY1, TRIGS, IFAC, WORK, LWORK, ERR)
|
|
SFFTCM [DFFTZM]
|
(OPT, N1, N2, SCALE, X, LDX1, Y, LDY1, TRIGS, IFAC, WORK, LWORK, ERR)
|
|
CFFTC [ZFFTZ]
|
(OPT, N1, SCALE, X, Y, TRIGS, IFAC, WORK, LWORK, ERR)
|
|
CFFTCM [ZFFTZM]
|
(OPT, N1, N2, SCALE, X, LDX1, Y, LDY1, TRIGS, IFAC, WORK, LWORK, ERR)
|
|
Two-Dimensional Routines
|
|
CFFTS2 [ZFFTD2]
|
(OPT, N1, N2, SCALE, X, LDX1, Y, LDY1, TRIGS, IFAC, WORK, LWORK, ERR)
|
|
SFFTC2 [DFFTZ2]
|
(OPT, N1, N2, SCALE, X, LDX1, Y, LDY1, TRIGS, IFAC, WORK, LWORK, ERR)
|
|
CFFTC2 [ZFFTZ2]
|
(OPT, N1, N2, SCALE, X, LDX1, Y, LDY1, TRIGS, IFAC, WORK, LWORK, ERR)
|
|
Three-Dimensional Routines
|
|
CFFTS3 [ZFFTD3]
|
(OPT, N1, N2, N3, SCALE, X, LDX1, LDX2, Y, LDY1, LDY2, TRIGS, IFAC, WORK, LWORK, ERR)
|
|
SFFTC3 [DFFTZ3]
|
(OPT, N1, N2, N3, SCALE, X, LDX1, LDX2, Y, LDY1, LDY2, TRIGS, IFAC, WORK, LWORK, ERR)
|
|
CFFTC3 [ZFFTZ3]
|
(OPT, N1, N2, N3, SCALE, X, LDX1, LDX2, Y, LDY1, LDY2, TRIGS, IFAC, WORK, LWORK, ERR)
|
Sun Performance Library FFT routines use the following arguments.
- OPT: Flag indicating whether the routine is called to initialize or to compute the transform.
- N1, N2, N3: Problem dimensions for one, two, and three dimensional transforms.
- X: Input array where X is of type COMPLEX if the routine is a complex-to-complex transform or a complex-to-real tranform. X is of type REAL for a real-to-complex transform.
- Y: Output array where Y is of type COMPLEX if the routine is a complex-to-complex transform or a real-to-complex tranform. Y is of type REAL for a complex-to-real transform.
- LDX1, LDX2 and LDY1, LDY2: LDX1 and LDX2 are the leading dimensions of the input array, and LDY1 and LDY2 are the leading dimensions of the output array. The FFT routines allow the output to overwrite the input, which is an in-place transform, or to be stored in a separate array apart from the input array, which is an out-of-place transform. In complex-to-complex tranforms, the input data is of the same size as the output data. However, real-to-complex and complex-to-real transforms have different memory requirements for input and output data. Care must be taken to ensure that the input array is large enough to acommodate the transform results when computing an in-place tranform.
- TRIGS: Array containing the trigonometric weights.
- IFAC: Array containing factors of the problem dimensions. The problem sizes are as follows:
- Linear FFT: Problem size of dimension N1
- Two-dimensional FFT: Problem size of dimensions N1 and N2
- Three-dimensional FFT: Problem size of dimensions N1, N2, and N3
While N1, N2, and N3 can be of any size, a real-to-complex or a complex-to-real transform can be computed most efficiently when
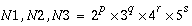
and a complex-to-complex transform can be computed most efficiently when
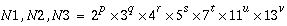
where p, q, r, s, t, u, and v are integers and p, q, r, s, t, u, v  0.
0.
- WORK: Workspace whose size depends on the routine and the number of threads that are being used to compute the transform if the routine is parallelized.
- LWORK: Size of workspace. If LWORK is zero, the routine will allocate a workspace with the required size.
- ERR: A flag returning a nonzero value if an error is encountered in the routine and zero otherwise.
Linear FFT Routines
Linear FFT routines compute the FFT of real or complex data in one dimension only. The data can be one or more complex or real sequences. For a single sequence, the data is stored in a vector. If more than one sequence is being transformed, the sequences are stored column-wise in a two-dimensional array and a one-dimensional FFT is computed for each sequence along the column direction. The linear forward FFT routines compute
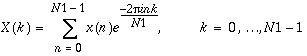 ,
,
where  , or expressed in polar form,
, or expressed in polar form,
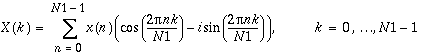 .
.
The inverse FFT routines compute
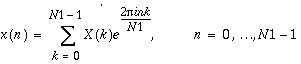 ,
,
or in polar form,
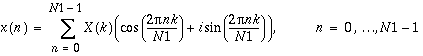 .
.
With the forward transform, if the input is one or more complex sequences of size N1, the result will be one or more complex sequences, each consisting of N1 unrelated data points. However, if the input is one or more real sequences, each containing N1 real data points, the result will be one or more complex sequences that are conjugate symmetric. That is,
 .
.
The imaginary part of X(0) is always zero. If N1 is even, the imaginary part of 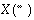 is also zero. Both zeros are stored explicitly. Because the second half of each sequence can be derived from the first half, only
is also zero. Both zeros are stored explicitly. Because the second half of each sequence can be derived from the first half, only  complex data points are computed and stored in the output array. Here and elsewhere in this chapter, integer division is rounded down.
complex data points are computed and stored in the output array. Here and elsewhere in this chapter, integer division is rounded down.
With the inverse transform, if an N1-point complex-to-complex transform is being computed, then N1 unrelated data points are expected in each input sequence and N1 data points will be returned in the output array. However, if an N1-point complex-to-real transform is being computed, only the first  complex data points of each conjugate symmetric input sequence are expected in the input, and the routine will return N1 real data points in each output sequence.
complex data points of each conjugate symmetric input sequence are expected in the input, and the routine will return N1 real data points in each output sequence.
For each value of N1, either the forward or the inverse routine must be called to compute the factors of N1 and the trigonometric weights associated with those factors before computing the actual FFT. The factors and trigonometric weights can be reused in subsequent transforms as long as N1 remains unchanged.
TABLE 6-2 lists the single precision linear FFT routines and their purposes. For routines that have two-dimensional arrays as input and output, TABLE 6-2 also lists the leading dimension requirements. The same information applies to the corresponding double precision routines except that their data types are double precision and double complex. See TABLE 6-2 for the mapping. See the individual man pages for a complete description of the routines and their arguments.
TABLE 6-2 Single Precision Linear FFT Routines
|
Name
|
Purpose
|
Size and Type
of Input
|
Size and Type
of Output
|
Leading Dimension Requirements
|
|
|
|
|
|
In-place
|
Out-of-Place
|
|
SFFTC
|
OPT = 0 initialization
|
|
|
|
|
|
|
OPT = -1 real-to-complex forward linear FFT of a single vector
|
N1,
Real
|
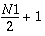 , ,
Complex
|
|
|
|
SFFTC
|
OPT = 0 initialization
|
|
|
|
|
|
|
OPT = 1 complex-to-real inverse linear FFT of single vector
|
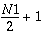 , ,
Complex
|
N1
Real
|
|
|
|
CFFTC
|
OPT = 0 initialization
|
|
|
|
|
|
|
OPT = -1 complex-to-complex forward linear FFT of a single vector
|
N1,
Complex
|
N1,
Complex
|
|
|
|
|
OPT = 1 complex-to-complex inverse linear FFT of a single vector
|
N1,
Complex
|
N1,
Complex
|
|
|
|
SFFTCM
|
OPT = 0 initialization
|
|
|
|
|
|
|
OPT = -1 real-to-complex forward linear FFT of M vectors
|
N1 × M,
Real
|
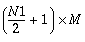 , ,
Complex
|
LDX1 = 2 × LDY1
|
LDX1  N1 N1
|
|
CFFTSM
|
OPT = 0 initialization
|
|
|
|
|
|
|
OPT = 1 complex-to-real inverse linear FFT of M vectors
|
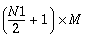 , ,
Complex
|
N1 × M,
Real
|
LDX1 
LDY1=2 × LDX1
|
LDX1 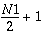
LDY1  N1 N1
|
|
CFFTCM
|
OPT = 0 initialization
|
|
|
|
|
|
|
OPT = -1 complex-to-complex forward linear FFT of M vectors
|
N1 × M,
Complex
|
N1 × M,
Complex
|
LDX1  N1 N1
LDY1  N1 N1
|
LDX1  N1 N1
LDY1  N1 N1
|
|
|
OPT = 1 complex-to-complex inverse linear FFT of M vectors
|
N1 × M,
Complex
|
N1 × M,
Complex
|
LDX1  N1 N1
LDY1  N1 N1
|
LDX1  N1 N1
LDY1  N1 N1
|
TABLE 6-2 Notes.
- LDX1 is the leading dimension of the input array.
- LDY1 is the leading dimension of the output array.
- N1 is the first dimension of the FFT problem.
- N2 is the second dimension of the FFT problem.
- When calling routines with OPT = 0 to initialize the routine, the only error checking that is done is to determine if N1 < 0
CODE EXAMPLE 6-1 shows how to compute the linear real-to-complex and complex-to-real FFT of a set of sequences.
CODE EXAMPLE 6-1 Linear Real-to-Complex FFT and Complex-to-Real FFT
my_system% cat testscm.f
PROGRAM TESTSCM
IMPLICIT NONE
INTEGER :: LW, IERR, I, J, K, LDX, LDC
INTEGER,PARAMETER :: N1 = 3, N2 = 2, LDZ = N1,
$ LDC = N1, LDX = 2*LDC
INTEGER, DIMENSION(:) :: IFAC(128)
REAL :: SCALE
REAL, PARAMETER :: ONE = 1.0
REAL, DIMENSION(:) :: SW(N1), TRIGS(2*N1)
REAL, DIMENSION(0:LDX-1,0:N2-1) :: X, V, Y
COMPLEX, DIMENSION(0:LDZ-1, 0:N2-1) :: Z
* workspace size LW = N1 SCALE = ONE/N1
WRITE(*,*) $ 'Linear complex-to-real and real-to-complex FFT of a sequence'
WRITE(*,*)
X = RESHAPE(SOURCE = (/.1, .2, .3,0.0,0.0,0.0,7.,8.,9.,
$ 0.0, 0.0, 0.0/), SHAPE=(/6,2/)) V = X
WRITE(*,*) 'X = '
DO I = 0,N1-1
WRITE(*,'(2(F4.1,2x))') (X(I,J), J = 0, N2-1)
END DO
WRITE(*,*)
* intialize trig table and compute factors of N1
CALL SFFTCM(0, N1, N2, ONE, X, LDX, Z, LDZ, TRIGS, IFAC,
$ SW, LW, IERR)
IF (IERR .NE. 0) THEN
PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
STOP
END IF
* Compute out-of-place forward linear FFT.
* Let FFT routine allocate memory.
CALL SFFTCM(-1, N1, N2, ONE, X, LDX, Z, LDZ, TRIGS, IFAC,
$ SW, 0, IERR)
IF (IERR .NE. 0) THEN
PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
STOP
END IF
WRITE(*,*) 'out-of-place forward FFT of X:'
WRITE(*,*)'Z ='
DO I = 0, N1/2
WRITE(*,'(2(A1, F4.1,A1,F4.1,A1,2x))') ('(',REAL(Z(I,J)),
$ ',',AIMAG(Z(I,J)),')', J = 0, N2-1)
END DO
WRITE(*,*)
* Compute in-place forward linear FFT.
* X must be large enough to store N1/2+1 complex values
CALL SFFTCM(-1, N1, N2, ONE, X, LDX, X, LDC, TRIGS, IFAC,
$ SW, LW, IERR)
IF (IERR .NE. 0) THEN
PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
STOP
END IF
WRITE(*,*) 'in-place forward FFT of X:'
CALL PRINT_REAL_AS_COMPLEX(N1/2+1, N2, 1, X, LDC, N2)
WRITE(*,*)
* Compute out-of-place inverse linear FFT.
CALL CFFTSM(1, N1, N2, SCALE, Z, LDZ, X, LDX, TRIGS, IFAC,
$ SW, LW, IERR)
IF (IERR .NE. 0) THEN
PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
STOP
END IF
WRITE(*,*) 'out-of-place inverse FFT of Z:'
DO I = 0, N1-1
WRITE(*,'(2(F4.1,2X))') (X(I,J), J = 0, N2-1)
END DO
WRITE(*,*)
* Compute in-place inverse linear FFT.
CALL CFFTSM(1, N1, N2, SCALE, Z, LDZ, Z, LDZ*2, TRIGS,
$ IFAC, SW, 0, IERR)
IF (IERR .NE. 0) THEN
PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
STOP
END IF
WRITE(*,*) 'in-place inverse FFT of Z:'
CALL PRINT_COMPLEX_AS_REAL(N1, N2, 1, Z, LDZ*2, N2)
WRITE(*,*)
END PROGRAM TESTSCM
SUBROUTINE PRINT_COMPLEX_AS_REAL(N1, N2, N3, A, LD1, LD2)
INTEGER N1, N2, N3, I, J, K
REAL A(LD1, LD2, *)
DO K = 1, N3
DO I = 1, N1
WRITE(*,'(5(F4.1,2X))') (A(I,J,K), J = 1, N2)
END DO
WRITE(*,*)
END DO
END
SUBROUTINE PRINT_REAL_AS_COMPLEX(N1, N2, N3, A, LD1, LD2)
INTEGER N1, N2, N3, I, J, K
COMPLEX A(LD1, LD2, *)
DO K = 1, N3
DO I = 1, N1
WRITE(*,'(5(A1, F4.1,A1,F4.1,A1,2X))') ('(',REAL(A(I,J,K)),
$ ',',AIMAG(A(I,J,K)),')', J = 1, N2)
END DO
WRITE(*,*)
END DO
END
my_system% f95 -dalign testscm.f -xlic_lib=sunperf
my_system% a.out
Linear complex-to-real and real-to-complex FFT of a sequence
X =
0.1 7.0
0.2 8.0
0.3 9.0
out-of-place forward FFT of X:
Z =
( 0.6, 0.0) (24.0, 0.0)
(-0.2, 0.1) (-1.5, 0.9)
in-place forward FFT of X:
( 0.6, 0.0) (24.0, 0.0)
(-0.2, 0.1) (-1.5, 0.9)
out-of-place inverse FFT of Z:
0.1 7.0
0.2 8.0
0.3 9.0
in-place inverse FFT of Z:
0.1 7.0
0.2 8.0
0.3 9.0
|
CODE EXAMPLE 6-1 Notes:
The forward FFT of X is actually
|
|
(0.6, 0.0)
|
(24.0, 0.0)
|
|
Z =
|
(-0.2, 0.1)
|
(-1.5, 0.9)
|
|
|
(-0.2, -0.1)
|
(-1.5, -0.9)
|
Because of symmetry, Z(2) is the complex conjugate of Z(1), and therefore only the first two 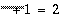 complex values are stored. For the in-place forward transform, SFFTCMis called with real array X as the input and output. Because SFFTCMexpects the output array to be of type COMPLEX, the leading dimension of X as an output array must be as if X were complex. Since the leading dimension of real array X is LDX= 2 ×LDC, the leading dimension of X as a complex output array must be LDC. Similarly, in the in-place inverse transform, CFFTSMis called with complex array Z as the input and output. Because CFFTSMexpects the output array to be of type REAL, the leading dimension of Z as an output array must be as if Z were real. Since the leading dimension of complex array Z is LDZ, the leading dimension of Z as a real output array must be LDZ×2.
complex values are stored. For the in-place forward transform, SFFTCMis called with real array X as the input and output. Because SFFTCMexpects the output array to be of type COMPLEX, the leading dimension of X as an output array must be as if X were complex. Since the leading dimension of real array X is LDX= 2 ×LDC, the leading dimension of X as a complex output array must be LDC. Similarly, in the in-place inverse transform, CFFTSMis called with complex array Z as the input and output. Because CFFTSMexpects the output array to be of type REAL, the leading dimension of Z as an output array must be as if Z were real. Since the leading dimension of complex array Z is LDZ, the leading dimension of Z as a real output array must be LDZ×2.
CODE EXAMPLE 6-2 shows how to compute the linear complex-to-complex FFT of a set of sequences.
CODE EXAMPLE 6-2 Linear Complex-to-Complex FFT
my_system% cat testccm.f
PROGRAM TESTCCM
IMPLICIT NONE
INTEGER :: LDX1, LDY1, LW, IERR, I, J, K, LDZ1, NCPUS,
$ USING_THREADS, IFAC(128)
INTEGER, PARAMETER :: N1 = 3, N2 = 4, LDX1 = N1, LDZ1 = N1,
$ LDY1 = N1+2
REAL, PARAMETER :: ONE = 1.0, SCALE = ONE/N1
COMPLEX :: Z(0:LDZ1-1,0:N2-1), X(0:LDX1-1,0:N2-1),
$ Y(0:LDY1-1,0:N2-1)
REAL :: TRIGS(2*N1)
REAL, DIMENSION(:), ALLOCATABLE :: SW
* get number of threads
NCPUS = USING_THREADS()
* workspace size
LW = 2 * N1 * NCPUS
WRITE(*,*)'Linear complex-to-complex FFT of one or more sequences'
WRITE(*,*)
ALLOCATE(SW(LW))
X = RESHAPE(SOURCE =(/(.1,.2),(.3,.4),(.5,.6),(.7,.8),(.9,1.0),
$ (1.1,1.2),(1.3,1.4),(1.5,1.6),(1.7,1.8),(1.9,2.0),(2.1,2.2),
$ (1.2,2.0)/), SHAPE=(/LDX1,N2/))
Z = X
WRITE(*,*) 'X = '
DO I = 0, N1-1
WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))') ('(',REAL(X(I,J)),
$ ',',AIMAG(X(I,J)),')', J = 0, N2-1)
END DO WRITE(*,*)
* intialize trig table and compute factors of N1
CALL CFFTCM(0, N1, N2, SCALE, X, LDX1, Y, LDY1, TRIGS, IFAC,
$ SW, LW, IERR)
IF (IERR .NE. 0) THEN
PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
STOP
END IF
* Compute out-of-place forward linear FFT.
* Let FFT routine allocate memory.
CALL CFFTCM(-1, N1, N2, ONE, X, LDX1, Y, LDY1, TRIGS, IFAC,
$ SW, 0, IERR)
IF (IERR .NE. 0) THEN
PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
STOP
END IF
* Compute in-place forward linear FFT. LDZ1 must equal LDX1
CALL CFFTCM(-1, N1, N2, ONE, Z, LDX1, Z, LDZ1, TRIGS,
$ IFAC, SW, 0, IERR)
WRITE(*,*) 'in-place forward FFT of X:'
DO I = 0, N1-1
WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))') ('(',REAL(Z(I,J)),
$ ',',AIMAG(Z(I,J)),')', J = 0, N2-1)
END DO
WRITE(*,*)
WRITE(*,*) 'out-of-place forward FFT of X:'
WRITE(*,*) 'Y ='
DO I = 0, N1-1
WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))') ('(',REAL(Y(I,J)),
$ ',',AIMAG(Y(I,J)),')', J = 0, N2-1)
END DO
WRITE(*,*)
* Compute in-place inverse linear FFT.
CALL CFFTCM(1, N1, N2, SCALE, Y, LDY1, Y, LDY1, TRIGS, IFAC,
$ SW, LW, IERR)
IF (IERR .NE. 0) THEN
PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
STOP
END IF
WRITE(*,*) 'in-place inverse FFT of Y:'
WRITE(*,*) 'Y ='
DO I = 0, N1-1
WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))') ('(',REAL(Y(I,J)),
$ ',',AIMAG(Y(I,J)),')', J = 0, N2-1)
END DO
DEALLOCATE(SW)
END PROGRAM TESTCCM
my_system% f95 -dalign testccm.f -xlic_lib=sunperf
my_system% a.out
Linear complex-to-complex FFT of one or more sequences
X =
( 0.1, 0.2) ( 0.7, 0.8) ( 1.3, 1.4) ( 1.9, 2.0)
( 0.3, 0.4) ( 0.9, 1.0) ( 1.5, 1.6) ( 2.1, 2.2)
( 0.5, 0.6) ( 1.1, 1.2) ( 1.7, 1.8) ( 1.2, 2.0)
in-place forward FFT of X:
( 0.9, 1.2) ( 2.7, 3.0) ( 4.5, 4.8) ( 5.2, 6.2)
( -0.5, -0.1) ( -0.5, -0.1) ( -0.5, -0.1) ( 0.4, -0.9)
( -0.1, -0.5) ( -0.1, -0.5) ( -0.1, -0.5) ( 0.1, 0.7)
out-of-place forward FFT of X:
Y =
( 0.9, 1.2) ( 2.7, 3.0) ( 4.5, 4.8) ( 5.2, 6.2)
( -0.5, -0.1) ( -0.5, -0.1) ( -0.5, -0.1) ( 0.4, -0.9)
( -0.1, -0.5) ( -0.1, -0.5) ( -0.1, -0.5) ( 0.1, 0.7)
in-place inverse FFT of Y:
Y =
( 0.1, 0.2) ( 0.7, 0.8) ( 1.3, 1.4) ( 1.9, 2.0)
( 0.3, 0.4) ( 0.9, 1.0) ( 1.5, 1.6) ( 2.1, 2.2)
( 0.5, 0.6) ( 1.1, 1.2) ( 1.7, 1.8) ( 1.2, 2.0)
|
Two-Dimensional FFT Routines
For the linear FFT routines, when the input is a two-dimensional array, the FFT is computed along one dimension only, namely, along the columns of the array. The two-dimensional FFT routines take a two-dimensional array as input and compute the FFT along both the column and row dimensions. Specifically, the forward two-dimensional FFT routines compute
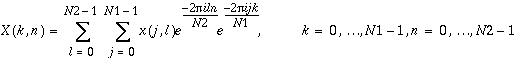 ,
,
and the inverse two-dimensional FFT routines compute
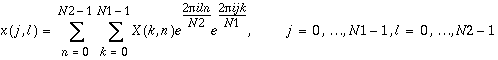 .
.
For both the forward and inverse two-dimensional transforms, a complex-to-complex transform where the input problem is N1 × N2 will yield a complex array that is also N1 × N2.
When computing a real-to-complex two-dimensional transform (forward FFT), if the real input array is of dimensions N1 ×N2, the result will be a complex array of dimensions ![(\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)X(\frac{N1}{2}+1:N1-1, [:)]X(0:\frac{N1}{2}, [:)] (\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)X(\frac{N1}{2}+1:N1-1, [:)]X(0:\frac{N1}{2}, [:)]](figures/plug_signal_proc-27.gif) . Conversely, when computing a complex-to-real transform (inverse FFT) of dimensions N1 ×N2, an
. Conversely, when computing a complex-to-real transform (inverse FFT) of dimensions N1 ×N2, an ![(\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)X(\frac{N1}{2}+1:N1-1, [:)]X(0:\frac{N1}{2}, [:)] (\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)X(\frac{N1}{2}+1:N1-1, [:)]X(0:\frac{N1}{2}, [:)]](figures/plug_signal_proc-28.gif) complex array is required as input. As with the real-to-complex and complex-to-real linear FFT, because of conjugate symmetry, only the first
complex array is required as input. As with the real-to-complex and complex-to-real linear FFT, because of conjugate symmetry, only the first ![(\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)X(\frac{N1}{2}+1:N1-1, [:)]X(0:\frac{N1}{2}, [:)] (\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)X(\frac{N1}{2}+1:N1-1, [:)]X(0:\frac{N1}{2}, [:)]](figures/plug_signal_proc-29.gif) complex data points need to be stored in the input or output array along the first dimension. The complex subarray
complex data points need to be stored in the input or output array along the first dimension. The complex subarray ![(\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)X(\frac{N1}{2}+1:N1-1, [:)]X(0:\frac{N1}{2}, [:)] (\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)X(\frac{N1}{2}+1:N1-1, [:)]X(0:\frac{N1}{2}, [:)]](figures/plug_signal_proc-30.gif) can be obtained from
can be obtained from ![(\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)X(\frac{N1}{2}+1:N1-1, [:)]X(0:\frac{N1}{2}, [:)] (\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)X(\frac{N1}{2}+1:N1-1, [:)]X(0:\frac{N1}{2}, [:)]](figures/plug_signal_proc-31.gif) as follows:
as follows:
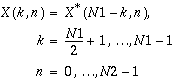
To compute a two-dimensional transform, an FFT routine must be called twice. One call initializes the routine and the second call actually computes the transform. The initialization includes computing the factors of N1 and N2 and the trigonometric weights associated with those factors. In subsequent forward or inverse transforms, initialization is not necessary as long as N1 and N2 remain unchanged.
IMPORTANT:Upon returning from a two-dimensional FFT routine, Y(0 : N- 1, :) contains the transform results and the original contents of Y(N : LDY-1, :) is overwritten. Here, N= N1 in the complex-to-complex and complex-to-real transforms and N=  in the real-to-complex transform.
in the real-to-complex transform.
TABLE 6-3 lists the single precision two-dimensional FFT routines and their purposes. The same information applies to the corresponding double precision routines except that their data types are double precision and double complex. See TABLE 6-3 for the mapping. Refer to the individual man pages for a complete description of the routines and their arguments.
TABLE 6-3 Single Precision Two-Dimensional FFT Routines
|
Name
|
Purpose
|
Size, Type of Input
|
Size, Type of Output
|
Leading Dimension Requirements
|
|
|
|
|
|
In-place
|
Out-of-Place
|
|
SFFTC2
|
OPT = 0 initialization
|
|
|
|
|
|
|
OPT = -1 real-to-complex forward two-dimensional FFT
|
N1 × N2, Real
|
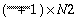 , ,
Complex
|
LDX1 = 2 × LDY1
LDY1 
|
LDX1  N1 N1
LDY1 
|
|
CFFTS2
|
OPT = 0 initialization
|
|
|
|
|
|
|
OPT = 1 complex-to-real inverse two-dimensional FFT
|
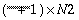 , ,
Complex
|
N1 × N2, Real
|
LDX1 
LDY1=2 × LDX1
|
LDX1 
LDY1 2 × LDX1 2 × LDX1
LDY1 is even
|
|
CFFTC2
|
OPT = 0 initialization
|
|
|
|
|
|
|
OPT = -1 complex-to-complex forward two-dimensional FFT
|
N1 × N2, Complex
|
N1 × N2, Complex
|
LDX1  N1 N1
LDY1 = LDX1
|
LDX1  N1 N1
LDY1  N1 N1
|
|
|
OPT = 1 complex-to-complex inverse two-dimensional FFT
|
N1 × N2, Complex
|
N1 × N2, Complex
|
LDX1  N1 N1
LDY1 = LDX1
|
LDX1  N1 N1
LDY1 = LDX1
|
TABLE 6-3 Notes:
- LDX1 is leading dimension of input array.
- LDY1 is leading dimension of output array.
- N1 is first dimension of the FFT problem.
- N2 is second dimension of the FFT problem.
- When calling routines with OPT = 0 to initialize the routine, the only error checking that is done is to determine if N1, N2 < 0.
The following example shows how to compute a two-dimensional real-to-complex FFT and complex-to-real FFT of a two-dimensional array.
CODE EXAMPLE 6-3 Two-Dimensional Real-to-Complex FFT and Complex-to-Real FFT of a Two-Dimensional Array
my_system% cat testsc2.f
PROGRAM TESTSC2
IMPLICIT NONE
INTEGER, PARAMETER :: N1 = 3, N2 = 4, LDX1 = N1,
$ LDY1 = N1/2+1, LDR1 = 2*(N1/2+1)
INTEGER LW, IERR, I, J, K, IFAC(128*2)
REAL, PARAMETER :: ONE = 1.0, SCALE = ONE/(N1*N2)
REAL :: V(LDR1,N2), X(LDX1, N2), Z(LDR1,N2),
$ SW(2*N2), TRIGS(2*(N1+N2))
COMPLEX :: Y(LDY1,N2)
WRITE(*,*) $'Two-dimensional complex-to-real and real-to-complex FFT'
WRITE(*,*)
X = RESHAPE(SOURCE = (/.1, .2, .3, .4, .5, .6, .7, .8,
$ 2.0,1.0, 1.1, 1.2/), SHAPE=(/LDX1,N2/))
DO I = 1, N2
V(1:N1,I) = X(1:N1,I)
END DO
WRITE(*,*) 'X ='
DO I = 1, N1
WRITE(*,'(5(F5.1,2X))') (X(I,J), J = 1, N2)
END DO
WRITE(*,*)
* Initialize trig table and get factors of N1, N2
CALL SFFTC2(0,N1,N2,ONE,X,LDX1,Y,LDY1,TRIGS,
$ IFAC,SW,0,IERR)
* Compute 2-dimensional out-of-place forward FFT.
* Let FFT routine allocate memory.
* cannot do an in-place transform in X because LDX1 < 2*(N1/2+1)
CALL SFFTC2(-1,N1,N2,ONE,X,LDX1,Y,LDY1,TRIGS,
$ IFAC,SW,0,IERR)
WRITE(*,*) 'out-of-place forward FFT of X:'
WRITE(*,*)'Y ='
DO I = 1, N1/2+1
WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))')('(',REAL(Y(I,J)),
$ ',',AIMAG(Y(I,J)),')', J = 1, N2)
END DO
WRITE(*,*)
* Compute 2-dimensional in-place forward FFT.
* Use workspace already allocated.
* V which is real array containing input data is also
* used to store complex results; as a complex array, its first
* leading dimension is LDR1/2.
CALL SFFTC2(-1,N1,N2,ONE,V,LDR1,V,LDR1/2,TRIGS,
$ IFAC,SW,LW,IERR)
WRITE(*,*) 'in-place forward FFT of X:'
CALL PRINT_REAL_AS_COMPLEX(N1/2+1, N2, 1, V, LDR1/2, N2)
* Compute 2-dimensional out-of-place inverse FFT.
* Leading dimension of Z must be even
CALL CFFTS2(1,N1,N2,SCALE,Y,LDY1,Z,LDR1,TRIGS,
$ IFAC,SW,0,IERR)
WRITE(*,*) 'out-of-place inverse FFT of Y:'
DO I = 1, N1
WRITE(*,'(5(F5.1,2X))') (Z(I,J), J = 1, N2)
END DO
WRITE(*,*)
* Compute 2-dimensional in-place inverse FFT.
* Y which is complex array containing input data is also
* used to store real results; as a real array, its first
* leading dimension is 2*LDY1.
CALL CFFTS2(1,N1,N2,SCALE,Y,LDY1,Y,2*LDY1,
$ TRIGS,IFAC,SW,0,IERR)
WRITE(*,*) 'in-place inverse FFT of Y:'
CALL PRINT_COMPLEX_AS_REAL(N1, N2, 1, Y, 2*LDY1, N2)
END PROGRAM TESTSC2
SUBROUTINE PRINT_COMPLEX_AS_REAL(N1, N2, N3, A, LD1, LD2)
INTEGER N1, N2, N3, I, J, K
REAL A(LD1, LD2, *)
DO K = 1, N3
DO I = 1, N1
WRITE(*,'(5(F5.1,2X))') (A(I,J,K), J = 1, N2)
END DO
WRITE(*,*)
END DO
END
SUBROUTINE PRINT_REAL_AS_COMPLEX(N1, N2, N3, A, LD1, LD2)
INTEGER N1, N2, N3, I, J, K
COMPLEX A(LD1, LD2, *)
DO K = 1, N3
DO I = 1, N1
WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))') ('(',REAL(A(I,J,K)),
$ ',',AIMAG(A(I,J,K)),')', J = 1, N2)
END DO
WRITE(*,*)
END DO
END
my_system% f95 -dalign testsc2.f -xlic_lib=sunperf
my_system% a.out
Two-dimensional complex-to-real and real-to-complex FFT
x =
0.1 0.4 0.7 1.0
0.2 0.5 0.8 1.1
0.3 0.6 2.0 1.2
out-of-place forward FFT of X:
Y =
( 8.9, 0.0) ( -2.9, 1.8) ( -0.7, 0.0) ( -2.9, -1.8)
( -1.2, 1.3) ( 0.5, -1.0) ( -0.5, 1.0) ( 0.5, -1.0)
in-place forward FFT of X:
( 8.9, 0.0) ( -2.9, 1.8) ( -0.7, 0.0) ( -2.9, -1.8)
( -1.2, 1.3) ( 0.5, -1.0) ( -0.5, 1.0) ( 0.5, -1.0)
out-of-place inverse FFT of Y:
0.1 0.4 0.7 1.0
0.2 0.5 0.8 1.1
0.3 0.6 2.0 1.2
in-place inverse FFT of Y:
0.1 0.4 0.7 1.0
0.2 0.5 0.8 1.1
0.3 0.6 2.0 1.2
|
Three-Dimensional FFT Routines
Sun Performance Library includes routines that compute three-dimensional FFT. In this case, the FFT is computed along all three dimensions of a three-dimensional array. The forward FFT computes
 ,
,
k = 0, ..., N1 - 1
n = 0, ..., N2 - 1
m = 0, ..., N3 - 1
and the inverse FFT computes
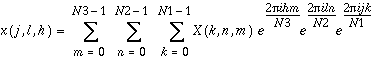 ,
,
j = 0, ..., N1 - 1
l = 0, ..., N2 - 1
h = 0, ..., N3 - 1
In the complex-to-complex transform, if the input problem is N1 ×N2 ×N3, a three-dimensional transform will yield a complex array that is also N1 ×N2 ×N3. When computing a real-to-complex three-dimensional transform, if the real input array is of dimensions N1 ×N2 ×N3, the result will be a complex array of dimensions ![(\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1) X(\frac{N1}{2}+1:N1-1,:, [:)]X(0:\frac{N1}{2},:, [:)] (\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1) X(\frac{N1}{2}+1:N1-1,:, [:)]X(0:\frac{N1}{2},:, [:)]](figures/plug_signal_proc-42.gif) . Conversely, when computing a complex-to-real FFT of dimensions N1 ×N2 ×N3, an
. Conversely, when computing a complex-to-real FFT of dimensions N1 ×N2 ×N3, an ![(\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1) X(\frac{N1}{2}+1:N1-1,:, [:)]X(0:\frac{N1}{2},:, [:)] (\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1) X(\frac{N1}{2}+1:N1-1,:, [:)]X(0:\frac{N1}{2},:, [:)]](figures/plug_signal_proc-43.gif) complex array is required as input. As with the real-to-complex and complex-to-real linear FFT, because of conjugate symmetry, only the first
complex array is required as input. As with the real-to-complex and complex-to-real linear FFT, because of conjugate symmetry, only the first ![(\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1) X(\frac{N1}{2}+1:N1-1,:, [:)]X(0:\frac{N1}{2},:, [:)] (\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1) X(\frac{N1}{2}+1:N1-1,:, [:)]X(0:\frac{N1}{2},:, [:)]](figures/plug_signal_proc-44.gif) complex data points need to be stored along the first dimension. The complex subarray
complex data points need to be stored along the first dimension. The complex subarray ![(\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1) X(\frac{N1}{2}+1:N1-1,:, [:)]X(0:\frac{N1}{2},:, [:)] (\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1) X(\frac{N1}{2}+1:N1-1,:, [:)]X(0:\frac{N1}{2},:, [:)]](figures/plug_signal_proc-45.gif) can be obtained from
can be obtained from ![(\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1) X(\frac{N1}{2}+1:N1-1,:, [:)]X(0:\frac{N1}{2},:, [:)] (\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1) X(\frac{N1}{2}+1:N1-1,:, [:)]X(0:\frac{N1}{2},:, [:)]](figures/plug_signal_proc-46.gif) as follows:
as follows:
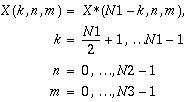
To compute a three-dimensional transform, an FFT routine must be called twice: Once to initialize and once more to actually compute the transform. The initialization includes computing the factors of N1, N2, and N3 and the trigonometric weights associated with those factors. In subsequent forward or inverse transforms, initialization is not necessary as long as N1, N2, and N3 remain unchanged.
IMPORTANT:Upon returning from a three-dimensional FFT routine, Y(0 : N - 1, :, :) contains the transform results and the original contents of Y(N:LDY1-1, :, :) is overwritten. Here, N = N1 in the complex-to-complex and complex-to-real transforms and N =  in the real-to-complex transform.
in the real-to-complex transform.
TABLE 6-4 lists the single precision three-dimensional FFT routines and their purposes. The same information applies to the corresponding double precision routines except that their data types are double precision and double complex. See TABLE 6-4 for the mapping. See the individual man pages for a complete description of the routines and their arguments.
TABLE 6-4 Single Precision Three-Dimensional FFT Routines
|
Name
|
Purpose
|
Size, Type of Input
|
Size, Type of Output
|
Leading Dimension Requirements
|
|
|
|
|
|
In-place
|
Out-of-Place
|
|
SFFTC3
|
OPT = 0 initialization
|
|
|
|
|
|
|
OPT = -1 real-to-complex forward three-dimensional FFT
|
N1 × N2 × N3, Real
|
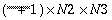 , ,
Complex
|
LDX1=2 × LDY1
LDX2  N2 N2
LDY1 
LDY2 = LDX2
|
LDX1  N1 N1
LDX2  N2 N2
LDY1 
LDY2  N2 N2
|
|
CFFTS3
|
OPT = 0 initialization
|
|
|
|
|
|
|
OPT = 1 complex-to-real inverse three-dimensional FFT
|
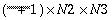 , ,
Complex
|
N1 × N2 × N3, Real
|
LDX1 
LDX2  N2 N2
LDY1=2 × LDX1
LDY2=LDX2
|
LDX1 
LDX2  N2 N2
LDY1  2 × LDX1 2 × LDX1
LDY1 is even
LDY2  N2 N2
|
|
CFFTC3
|
OPT = 0 initialization
|
|
|
|
|
|
|
OPT = -1 complex-to-complex forward three-dimensional FFT
|
N1 × N2 × N3,
Complex
|
N1 × N2 × N3,
Complex
|
LDX1  N1 N1
LDX2  N2 N2
LDY1=LDX1
LDY2=LDX2
|
LDX1  N1 N1
LDX2  N2 N2
LDY1  N1 N1
LDY2  N2 N2
|
|
|
OPT = 1 complex-to-complex inverse three-dimensional FFT
|
N1 × N2 × N3,
Complex
|
N1 × N2 × N3,
Complex
|
LDX1  N1 N1
LDX2  N2 N2
LDY1=LDX1
LDY2=LDX2
|
LDX1  N1 N1
LDX2  N2 N2
LDY1  N1 N1
LDY2  N2 N2
|
TABLE 6-4 Notes:
- LDX1 is first leading dimension of input array.
- LDX2 is the second leading dimension of the input array.
- LDY1 is the first leading dimension of the output array.
- LDY2 is the second leading dimension of the output array.
- N1 is the first dimension of the FFT problem.
- N2 is the second dimension of the FFT problem.
- N3 is the third dimension of the FFT problem.
- When calling routines with OPT = 0 to initialize the routine, the only error checking that is done is to determine if N1, N2, N3 < 0.
CODE EXAMPLE 6-4 shows how to compute the three-dimensional real-to-complex FFT and complex-to-real FFT of a three-dimensional array.
CODE EXAMPLE 6-4 Three-Dimensional Real-to-Complex FFT and Complex-to-Real FFT of a Three-Dimensional Array
my_system% cat testsc3.f
PROGRAM TESTSC3
IMPLICIT NONE
INTEGER LW, NCPUS, IERR, I, J, K, USING_THREADS, IFAC(128*3)
INTEGER, PARAMETER :: N1 = 3, N2 = 4, N3 = 2, LDX1 = N1,
$ LDX2 = N2, LDY1 = N1/2+1, LDY2 = N2,
$ LDR1 = 2*(N1/2+1), LDR2 = N2
REAL, PARAMETER :: ONE = 1.0, SCALE = ONE/(N1*N2*N3)
REAL :: V(LDR1,LDR2,N3), X(LDX1,LDX2,N3), Z(LDR1,LDR2,N3),
$ TRIGS(2*(N1+N2+N3))
REAL, DIMENSION(:), ALLOCATABLE :: SW
COMPLEX :: Y(LDY1,LDY2,N3)
WRITE(*,*) $'Three-dimensional complex-to-real and real-to-complex FFT'
WRITE(*,*)
* get number of threads
NCPUS = USING_THREADS()
* compute workspace size required
LW = (MAX(MAX(N1,2*N2),2*N3) + 16*N3) * NCPUS
ALLOCATE(SW(LW))
X = RESHAPE(SOURCE =
$ (/ .1, .2, .3, .4, .5, .6, .7, .8, .9,1.0,1.1,1.2,
$ 4.1,1.2,2.3,3.4,6.5,1.6,2.7,4.8,7.9,1.0,3.1,2.2/),
$ SHAPE=(/LDX1,LDX2,N3/))
V = RESHAPE(SOURCE =
$ (/.1,.2,.3,0.,.4,.5,.6,0.,.7,.8,.9,0.,1.0,1.1,1.2,0.,
$ 4.1,1.2,2.3,0.,3.4,6.5,1.6,0.,2.7,4.8,7.9,0.,
$ 1.0,3.1,2.2,0./), SHAPE=(/LDR1,LDR2,N3/))
WRITE(*,*) 'X ='
DO K = 1, N3
DO I = 1, N1
WRITE(*,'(5(F5.1,2X))') (X(I,J,K), J = 1, N2)
END DO
WRITE(*,*)
END DO
* Initialize trig table and get factors of N1, N2 and N3
CALL SFFTC3(0,N1,N2,N3,ONE,X,LDX1,LDX2,Y,LDY1,LDY2,TRIGS,
$ IFAC,SW,0,IERR)
* Compute 3-dimensional out-of-place forward FFT.
* Let FFT routine allocate memory.
* cannot do an in-place transform because LDX1 < 2*(N1/2+1)
CALL SFFTC3(-1,N1,N2,N3,ONE,X,LDX1,LDX2,Y,LDY1,LDY2,TRIGS,
$ IFAC,SW,0,IERR)
WRITE(*,*) 'out-of-place forward FFT of X:'
WRITE(*,*)'Y ='
DO K = 1, N3
DO I = 1, N1/2+1
WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))')('(',REAL(Y(I,J,K)),
$ ',',AIMAG(Y(I,J,K)),')', J = 1, N2)
END DO
WRITE(*,*)
END DO
* Compute 3-dimensional in-place forward FFT.
* Use workspace already allocated.
* V which is real array containing input data is also
* used to store complex results; as a complex array, its first
* leading dimension is LDR1/2.
CALL SFFTC3(-1,N1,N2,N3,ONE,V,LDR1,LDR2,V,LDR1/2,LDR2,TRIGS,
$ IFAC,SW,LW,IERR)
WRITE(*,*) 'in-place forward FFT of X:'
CALL PRINT_REAL_AS_COMPLEX(N1/2+1, N2, N3, V, LDR1/2, LDR2)
* Compute 3-dimensional out-of-place inverse FFT.
* First leading dimension of Z (LDR1) must be even
CALL CFFTS3(1,N1,N2,N3,SCALE,Y,LDY1,LDY2,Z,LDR1,LDR2,TRIGS,
$ IFAC,SW,0,IERR)
WRITE(*,*) 'out-of-place inverse FFT of Y:'
DO K = 1, N3
DO I = 1, N1
WRITE(*,'(5(F5.1,2X))') (Z(I,J,K), J = 1, N2)
END DO
WRITE(*,*)
END DO
* Compute 3-dimensional in-place inverse FFT.
* Y which is complex array containing input data is also
* used to store real results; as a real array, its first
* leading dimension is 2*LDY1.
CALL CFFTS3(1,N1,N2,N3,SCALE,Y,LDY1,LDY2,Y,2*LDY1,LDY2,
$ TRIGS,IFAC,SW,LW,IERR)
WRITE(*,*) 'in-place inverse FFT of Y:'
CALL PRINT_COMPLEX_AS_REAL(N1, N2, N3, Y, 2*LDY1, LDY2)
DEALLOCATE(SW)
END PROGRAM TESTSC3
SUBROUTINE PRINT_COMPLEX_AS_REAL(N1, N2, N3, A, LD1, LD2)
INTEGER N1, N2, N3, I, J, K
REAL A(LD1, LD2, *)
DO K = 1, N3
DO I = 1, N1
WRITE(*,'(5(F5.1,2X))') (A(I,J,K), J = 1, N2)
END DO
WRITE(*,*)
END DO
END
SUBROUTINE PRINT_REAL_AS_COMPLEX(N1, N2, N3, A, LD1, LD2)
INTEGER N1, N2, N3, I, J, K COMPLEX A(LD1, LD2, *)
DO K = 1, N3
DO I = 1, N1
WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))') ('(',REAL(A(I,J,K)),
$ ',',AIMAG(A(I,J,K)),')', J = 1, N2)
END DO
WRITE(*,*)
END DO
END
my_system% f95 -dalign testsc3.f -xlic_lib=sunperf
my_system% a.out
Three-dimensional complex-to-real and real-to-complex FFT
X =
0.1 0.4 0.7 1.0
0.2 0.5 0.8 1.1
0.3 0.6 0.9 1.2
4.1 3.4 2.7 1.0
1.2 6.5 4.8 3.1
2.3 1.6 7.9 2.2
out-of-place forward FFT of X:
Y =
( 48.6, 0.0) ( -9.6, -3.4) ( 3.4, 0.0) ( -9.6, 3.4)
( -4.2, -1.0) ( 2.5, -2.7) ( 1.0, 8.7) ( 9.5, -0.7)
(-33.0, 0.0) ( 6.0, 7.0) ( -7.0, 0.0) ( 6.0, -7.0)
( 3.0, 1.7) ( -2.5, 2.7) ( -1.0, -8.7) ( -9.5, 0.7)
in-place forward FFT of X:
( 48.6, 0.0) ( -9.6, -3.4) ( 3.4, 0.0) ( -9.6, 3.4)
( -4.2, -1.0) ( 2.5, -2.7) ( 1.0, 8.7) ( 9.5, -0.7)
(-33.0, 0.0) ( 6.0, 7.0) ( -7.0, 0.0) ( 6.0, -7.0)
( 3.0, 1.7) ( -2.5, 2.7) ( -1.0, -8.7) ( -9.5, 0.7)
out-of-place inverse FFT of Y:
0.1 0.4 0.7 1.0
0.2 0.5 0.8 1.1
0.3 0.6 0.9 1.2
4.1 3.4 2.7 1.0
1.2 6.5 4.8 3.1
2.3 1.6 7.9 2.2
in-place inverse FFT of Y:
0.1 0.4 0.7 1.0
0.2 0.5 0.8 1.1
0.3 0.6 0.9 1.2
4.1 3.4 2.7 1.0
1.2 6.5 4.8 3.1
2.3 1.6 7.9 2.2
|
Comments
When doing an in-place real-to-complex or complex-to-real transform, care must be taken to ensure the size of the input array is large enough to hold the results. For example, if the input is of type complex stored in a complex array with first leading dimension N, then to use the same array to store the real results, its first leading dimension as a real output array would be 2 × N. Conversely, if the input is of type real stored in a real array with first leading dimension 2 × N, then to use the same array to store the complex results, its first leading dimension as a complex output array would be N. Leading dimension requirements for in-place and out-of-place transforms can be found in TABLE 6-2, TABLE 6-3, and TABLE 6-4.
In the linear and multi-dimensional FFT, the transform between real and complex data through a real-to-complex or complex-to-real transform can be confusing because N1 real data points correspond to  complex data points. N1 real data points do map to N1 complex data points, but because there is conjugate symmetry in the complex data, only
complex data points. N1 real data points do map to N1 complex data points, but because there is conjugate symmetry in the complex data, only  data points need to be stored as input in the complex-to-real transform and as output in the real-to-complex transform. In the multi-dimensional FFT, symmetry exists along all the dimensions, not just in the first. However, the two-dimensional and three-dimensional FFT routines store the complex data of the second and third dimensions in their entirety.
data points need to be stored as input in the complex-to-real transform and as output in the real-to-complex transform. In the multi-dimensional FFT, symmetry exists along all the dimensions, not just in the first. However, the two-dimensional and three-dimensional FFT routines store the complex data of the second and third dimensions in their entirety.
While the FFT routines accept any size of N1, N2 and N3, FFTs can be computed most efficiently when values of N1, N2 and N3 can be decomposed into relatively small primes. A real-to-complex or a complex-to-real transform can be computed most efficiently when
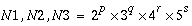 ,
,
and a complex-to-complex transform can be computed most efficiently when
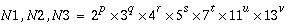 ,
,
where p, q, r, s, t, u, and v are integers and p, q, r, s, t, u, v  0.
0.
The function xFFTOPT can be used to determine the optimal sequence length, as shown in CODE EXAMPLE 6-5.
CODE EXAMPLE 6-5 RFFTOPT Example
my_system% cat fft_ex01.f
PROGRAM TEST
INTEGER N, N1, N2, N3, RFFTOPT
C
N = 1024
N1 = 1019
N2 = 71
N3 = 49
C
PRINT *, 'N Original N Suggested'
PRINT '(I5, I12)', (N, RFFTOPT(N))
PRINT '(I5, I12)', (N1, RFFTOPT(N1))
PRINT '(I5, I12)', (N2, RFFTOPT(N2))
PRINT '(I5, I12)', (N3, RFFTOPT(N3))
END
my_system% f95 -dalign fft_ex01.f -xlic_lib=sunperf
my_system% a.out
N Original N Suggested
1024 1024
1019 1024
71 72
49 49
|
Cosine and Sine Transforms
Input to the DFT that possess special symmetries occur in various applications. A transform that exploits symmetry usually saves in storage and computational count, such as with the real-to-complex and complex-to-real FFT transforms. The Sun Performance Library cosine and sine transforms are special cases of FFT routines that take advantage of the symmetry properties found in even and odd functions.
Fast Cosine and Sine Transform Routines
TABLE 6-5 lists the Sun Performance Library fast cosine and sine transforms. Names of double precision routines are in square brackets. Routines whose name begins with 'V' can compute the transform of one or more sequences simultaneously. Those whose name ends with 'I' are initialization routines.
TABLE 6-5 Fast Cosine and Sine Transform Routines and Their Arguments
|
Name
|
Arguments
|
|
Fast Cosine Transforms for Even Sequences
|
|
COST [DCOST]
|
(LEN+1, X, WORK)
|
|
COSTI [DCOSTI]
|
(LEN+1, WORK)
|
|
VCOST [VDCOST]
|
(M, LEN+1, X, WORK, LD, TABLE)
|
|
VCOSTI [VDCOSTI]
|
(LEN+1, TABLE)
|
|
Fast Cosine Transforms for Quarter-Wave Even Sequences
|
|
COSQF [DCOSQF]
|
(LEN, X, WORK)
|
|
COSQB [DCOSQB]
|
(LEN, X, WORK)
|
|
COSQI [DCOSQI]
|
(LEN, WORK)
|
|
VCOSQF [VDCOSQF]
|
(M, LEN, X, WORK, LD, TABLE)
|
|
VCOSQB [VDCOSQB]
|
(M, LEN, X, WORK, LD, TABLE)
|
|
VCOSQI [VDCOSQI]
|
(LEN, TABLE)
|
|
Fast Sine Transforms for Odd Sequences
|
|
SINT [DSINT]
|
(LEN-1, X, WORK)
|
|
SINTI [DSINTI]
|
(LEN-1, WORK)
|
|
VSINT [VDSINT]
|
(M, LEN-1, X, WORK, LD, TABLE)
|
|
VSINTI [VDSINTI]
|
(LEN-1, TABLE)
|
|
Fast Sine Transforms for Quarter-Wave Odd Sequences
|
|
SINQF [DSINQF]
|
(LEN, X, WORK)
|
|
SINQB [DSINQB]
|
(LEN, X, WORK)
|
|
SINQI [DSINQI]
|
(LEN, WORK)
|
|
VSINQF [VDSINQF]
|
(M, LEN, X, WORK, LD, TABLE)
|
|
VSINQB [VDSINQB]
|
(M, LEN, X, WORK, LD, TABLE)
|
|
VSINQI [VDSINQI]
|
(LEN, TABLE)
|
TABLE 6-5 Notes:
- M: Number of sequences to be transformed.
- LEN, LEN-1, LEN+1: Length of the input sequence or sequences.
- X: A real array which contains the sequence or sequences to be transformed. On output, the real transform results are stored in X.
- TABLE: Array of constants particular to a transform size that is required by the transform routine. The constants are computed by the initialization routine.
- WORK: Workspace required by the transform routine. In routines that operate on a single sequence, WORK also contains constants computed by the initialization routine.
Fast Cosine Transforms
A special form of the FFT that operates on real even sequences is the fast cosine transform (FCT). A real sequence x is said to have even symmetry if x(n) = x(-n) where n = -N + 1, ..., 0, ..., N. An FCT of a sequence of length 2N requires N + 1 input data points and produces a sequence of size N + 1. Routine COST computes the FCT of a single real even sequence while VCOST computes the FCT of one or more sequences. Before calling [V]COST, [V]COSTI must be called to compute trigonometric constants and factors associated with input length N + 1. The FCT is its own inverse transform. Calling VCOST twice will result in the original N +1 data points. Calling COST twice will result in the original N +1 data points multiplied by 2N.
An even sequence xwith symmetry such that x(n) = x(-n - 1) where n= -N + 1, ... , 0, ..., Nis said to have quarter-wave even symmetry. COSQFand COSQBcompute the FCT and its inverse, respectively, of a single real quarter-wave even sequence. VCOSQFand VCOSQBoperate on one or more sequences. The results of [V]COSQBare unormalized, and if scaled by  , the original sequences are obtained. An FCT of a real sequence of length 2Nthat has quarter-wave even symmetry requires Ninput data points and produces an N-point resulting sequence. Initialization is required before calling the transform routines by calling [V]COSQI.
, the original sequences are obtained. An FCT of a real sequence of length 2Nthat has quarter-wave even symmetry requires Ninput data points and produces an N-point resulting sequence. Initialization is required before calling the transform routines by calling [V]COSQI.
Fast Sine Transforms
Another type of symmetry that is commonly encountered is the odd symmetry where x(n) = -x(-n) for n = -N+1, ..., 0, ..., N. As in the case of the fast cosine transform, the fast sine transform (FST) takes advantage of the odd symmetry to save memory and computation. For a real odd sequence x, symmetry implies that x(0) = -x(0) = 0. Therefore, if x is of length 2N then only N = 1 values of x are required to compute the FST. Routine SINT computes the FST of a single real odd sequence while VSINT computes the FST of one or more sequences. Before calling [V]SINT, [V]SINTI must be called to compute trigonometric constants and factors associated with input length N - 1. The FST is its own inverse transform. Calling VSINT twice will result in the original N -1 data points. Calling SINT twice will result in the original N -1 data points multiplied by 2N.
An odd sequence with symmetry such that x(n) = -x(-n - 1), where n = -N + 1, ..., 0, ..., N is said to have quarter-wave odd symmetry. SINQF and SINQB compute the FST and its inverse, respectively, of a single real quarter-wave odd sequence while VSINQF and VSINQB operate on one or more sequences. SINQB is unnormalized, so using the results of SINQF as input in SINQB produces the original sequence scaled by a factor of 4N. However, VSINQB is normalized, so a call to VSINQF followed by a call to VSINQB will produce the original sequence. An FST of a real sequence of length 2N that has quarter-wave odd symmetry requires N input data points and produces an N-point resulting sequence. Initialization is required before calling the transform routines by calling [V]SINQI.
Discrete Fast Cosine and Sine Transforms and Their Inverse
Sun Performance Library routines use the equations in the following sections to compute the fast cosine and sine transforms and inverse transforms.
[D]COST: Forward and Inverse Fast Cosine Transform (FCT) of a Sequence
The forward and inverse FCT of a sequence is computed as
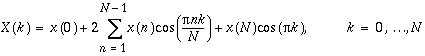 .
.
[D]COST Notes:
- N + 1 values are needed to compute the FCT of an N-point sequence.
- [D]COSTalso computes the inverse transform. When [D]COSTis called twice, the result will be the original sequence scaled by
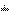 .
.
V[D]COST: Forward and Inverse Fast Cosine Transforms of Multiple Sequences (VFCT)
The forward and inverse FCTs of multiple sequences are computed as
For i = 0, M - 1
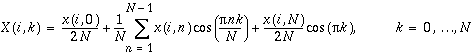 .
.
V[D]COST Notes
- M × (N+1) values are needed to compute the VFCT of M N-point sequences.
- The input and output sequences are stored row-wise.
- V[D]COST is normalized and is its own inverse. When V[D]COST is called twice, the result will be the original data.
[D]COSQF: Forward FCT of a Quarter-Wave Even Sequence
The forward FCT of a quarter-wave even sequence is computed as
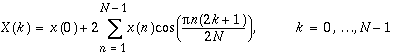 .
.
N values are needed to compute the forward FCT of an N-point quarter-wave even sequence.
[D]COSQB: Inverse FCT of a Quarter-Wave Even Sequence
The inverse FCT of a quarter-wave even sequence is computed as
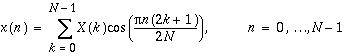 .
.
Calling the forward and inverse routines will result in the original input scaled by 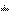 .
.
V[D]COSQF: Forward FCT of One or More Quarter-Wave Even Sequences
The forward FCT of one or more quarter-wave even sequences is computed as
For i = 0, M - 1
![X(i,k)=\frac{1}{N}\left[ x(i,0)+2\sum _{n=1}^{N-1}x(i,n)\cos (\frac{\pi n(2k+1)}{2N})\right] , k=0,\ldots N-1 X(i,k)=\frac{1}{N}\left[ x(i,0)+2\sum _{n=1}^{N-1}x(i,n)\cos (\frac{\pi n(2k+1)}{2N})\right] , k=0,\ldots N-1](figures/plug_signal_proc-67.gif) .
.
V[D]COSQF Notes:
- The input and output sequences are stored row-wise.
- The transform is normalized so that if the inverse routine V[D]COSQB is called immediately after calling V[D]COSQF, the original data is obtained.
V[D]COSQB: Inverse FCT of One or More Quarter-Wave Even Sequences
The inverse FCT of one or more quarter-wave even sequences is computed as
For i = 0, M - 1
 .
.
V[D]COSQB Notes:
- The input and output sequences are stored row-wise.
- The transform is normalized so that if V[D]COSQB is called immediately after calling V[D]COSQF, the original data is obtained.
[D]SINT: Forward and Inverse Fast Sine Transform (FST) of a Sequence
The forward and inverse FST of a sequence is computed as
 .
.
[D]SINT Notes:
- N-1 values are needed to compute the FST of an N-point sequence.
- [D]SINTalso computes the inverse transform. When [D]SINTis called twice, the result will be the original sequence scaled by
 .
.
V[D]SINT: Forward and Inverse Fast Sine Transforms of Multiple Sequences (VFST)
The forward and inverse fast sine transforms of multiple sequences are computed as
For i = 0, M - 1
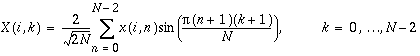 .
.
V[D]SINT Notes:
- M × (N - 1) values are needed to compute the VFST of M N-point sequences.
- The input and output sequences are stored row-wise.
- V[D]SINT is normalized and is its own inverse. Calling V[D]SINT twice yields the original data.
[D]SINQF: Forward FST of a Quarter-Wave Odd Sequence
The forward FST of a quarter-wave odd sequence is computed as
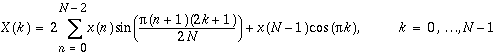 .
.
N values are needed to compute the forward FST of an N-point quarter-wave odd sequence.
[D]SINQB: Inverse FST of a Quarter-Wave Odd Sequence
The inverse FST of a quarter-wave odd sequence is computed as
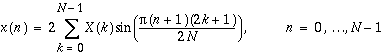 .
.
Calling the forward and inverse routines will result in the original input scaled by  .
.
V[D]SINQF: Forward FST of One or More Quarter-Wave Odd Sequences
The forward FST of one or more quarter-wave odd sequences is computed as
For i = 0, M - 1
![X(i,k)=\frac{1}{\sqrt{4N}}\left[ 2\sum _{n=0}^{N-2}x(n,i)\sin (\frac{\pi (n+1)(2k+1)}{2N})+x(N-1,i)\cos (\pi k)\right] , k=0,\ldots N-1 X(i,k)=\frac{1}{\sqrt{4N}}\left[ 2\sum _{n=0}^{N-2}x(n,i)\sin (\frac{\pi (n+1)(2k+1)}{2N})+x(N-1,i)\cos (\pi k)\right] , k=0,\ldots N-1](figures/plug_signal_proc-75.gif) .
.
V[D]SINQF Notes:
- The input and output sequences are stored row-wise.
- The transform is normalized so that if the inverse routine V[D]SINQB is called immediately after calling V[D]SINQF, the original data is obtained.
V[D]SINQB: Inverse FST of One or More Quarter-Wave Odd Sequences
The inverse FST of one or more quarter-wave odd sequences is computed as
For i = 0, M - 1
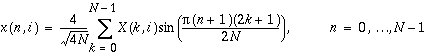 .
.
V[D]SINQB Notes:
- The input and output sequences are stored row-wise.
- The transform is normalized, so that if V[D]SINQB is called immediately after calling V[D]SINQF, the original data is obtained.
Fast Cosine Transform Examples
CODE EXAMPLE 6-6 calls COST to compute the FCT and the inverse transform of a real even sequence. If the real sequence is of length 2N, only N + 1 input data points need to be stored and the number of resulting data points is also N + 1. The results are stored in the input array.
CODE EXAMPLE 6-6 Compute FCT and Inverse FCT of Single Real Even Sequence
my_system% cat cost.f
program cost
implicit none
integer,parameter :: len=4
real x(0:len),work(3*(len+1)+15), z(0:len), scale
integer i
scale = 1.0/(2.0*len)
call RANDOM_NUMBER(x(0:len))
z(0:len) = x(0:len)
write(*,'(a25,i1,a10,i1,a12)')'Input sequence of length ',
$ len,' requires ', len+1,' data points'
write(*,'(5(f8.3,2x),/)')(x(i),i=0,len)
call costi(len+1, work)
call cost(len+1, z, work)
write(*,*)'Forward fast cosine transform'
write(*,'(5(f8.3,2x),/)')(z(i),i=0,len)
call cost(len+1, z, work)
write(*,*)
$ 'Inverse fast cosine transform (results scaled by 1/2*N)'
write(*,'(5(f8.3,2x),/)')(z(i)*scale,i=0,len)
end
my_system% f95 -dalign cost.f -xlic_lib=sunperf
my_system% a.out
Input sequence of length 4 requires 5 data points
0.557 0.603 0.210 0.352 0.867
Forward fast cosine transform
3.753 0.046 1.004 -0.666 -0.066
Inverse fast cosine transform (results scaled by 1/2*N)
0.557 0.603 0.210 0.352 0.867
|
CODE EXAMPLE 6-7 calls VCOSQF and VCOSQB to compute the FCT and the inverse FCT, respectively, of two real quarter-wave even sequences. If the real sequences are of length 2N, only N input data points need to be stored, and the number of resulting data points is also N. The results are stored in the input array.
CODE EXAMPLE 6-7 Compute the FCT and the Inverse FCT of Two Real Quarter-wave Even Sequences
my_system% cat vcosq.f
program vcosq
implicit none
integer,parameter :: len=4, m = 2, ld = m+1
real x(ld,len),xt(ld,len),work(3*len+15), z(ld,len)
integer i, j
call RANDOM_NUMBER(x)
z = x
write(*,'(a27,i1)')' Input sequences of length ',len
do j = 1,m
write(*,'(a3,i1,a4,4(f5.3,2x),a1,/)')
$ 'seq',j,' = (',(x(j,i),i=1,len),')'
end do
call vcosqi(len, work)
call vcosqf(m,len, z, xt, ld, work)
write(*,*)
$ 'Forward fast cosine transform for quarter-wave even sequences'
do j = 1,m
write(*,'(a3,i1,a4,4(f5.3,2x),a1,/)')
$ 'seq',j,' = (',(z(j,i),i=1,len),')'
end do
call vcosqb(m,len, z, xt, ld, work)
write(*,*)
$ 'Inverse fast cosine transform for quarter-wave even sequences'
write(*,*)'(results are normalized)'
do j = 1,m
write(*,'(a3,i1,a4,4(f5.3,2x),a1,/)')
$ 'seq',j,' = (',(z(j,i),i=1,len),')'
end do
end
my_system% f95 -dalign vcosq.f -xlic_lib=sunperf
my_system% a.out
Input sequences of length 4
seq1 = (0.557 0.352 0.990 0.539 )
seq2 = (0.603 0.867 0.417 0.156 )
Forward fast cosine transform for quarter-wave even sequences
seq1 = (0.755 -.392 -.029 0.224 )
seq2 = (0.729 0.097 -.091 -.132 )
Inverse fast cosine transform for quarter-wave even sequences
(results are normalized)
seq1 = (0.557 0.352 0.990 0.539 )
seq2 = (0.603 0.867 0.417 0.156 )
|
Fast Sine Transform Examples
In CODE EXAMPLE 6-8, SINT is called to compute the FST and the inverse transform of a real odd sequence. If the real sequence is of length 2N, only N - 1 input data points need to be stored and the number of resulting data points is also N - 1. The results are stored in the input array.
CODE EXAMPLE 6-8 Compute FST and the Inverse FST of a Real Odd Sequence
my_system% cat sint.f
program sint
implicit none
integer,parameter :: len=4
real x(0:len-2),work(3*(len-1)+15), z(0:len-2), scale
integer i
call RANDOM_NUMBER(x(0:len-2))
z(0:len-2) = x(0:len-2)
scale = 1.0/(2.0*len)
write(*,'(a25,i1,a10,i1,a12)')'Input sequence of length ',
$ len,' requires ', len-1,' data points'
write(*,'(3(f8.3,2x),/)')(x(i),i=0,len-2)
call sinti(len-1, work)
call sint(len-1, z, work)
write(*,*)'Forward fast sine transform'
write(*,'(3(f8.3,2x),/)')(z(i),i=0,len-2)
call sint(len-1, z, work)
write(*,*) $ 'Inverse fast sine transform (results scaled by 1/2*N)'
write(*,'(3(f8.3,2x),/)')(z(i)*scale,i=0,len-2)
end
my_system% f95 -dalign sint.f -xlic_lib=sunperf
my_system% a.out
Input sequence of length 4 requires 3 data points
0.557 0.603 0.210
Forward fast sine transform
2.291 0.694 -0.122
Inverse fast sine transform (results scaled by 1/2*N)
0.557 0.603 0.210
|
In CODE EXAMPLE 6-9 VSINQF and VSINQB are called to compute the FST and inverse FST, respectively, of two real quarter-wave odd sequences. If the real sequence is of length 2N, only N input data points need to be stored and the number of resulting data points is also N. The results are stored in the input array.
CODE EXAMPLE 6-9 Compute FST and Inverse FST of Two Real Quarter-Wave Odd Sequences
my_system% cat vsinq.f
program vsinq
implicit none
integer,parameter :: len=4, m = 2, ld = m+1
real x(ld,len),xt(ld,len),work(3*len+15), z(ld,len)
integer i, j
call RANDOM_NUMBER(x)
z = x
write(*,'(a27,i1)')' Input sequences of length ',len
do j = 1,m
write(*,'(a3,i1,a4,4(f5.3,2x),a1,/)')
$ 'seq',j,' = (',(x(j,i),i=1,len),')'
end do
call vsinqi(len, work)
call vsinqf(m,len, z, xt, ld, work)
write(*,*)
$ 'Forward fast sine transform for quarter-wave odd sequences'
do j = 1,m
write(*,'(a3,i1,a4,4(f5.3,2x),a1,/)')
$ 'seq',j,' = (',(z(j,i),i=1,len),')'
end do
call vsinqb(m,len, z, xt, ld, work)
write(*,*)
$ 'Inverse fast sine transform for quarter-wave odd sequences'
write(*,*)'(results are normalized)'
do j = 1,m
write(*,'(a3,i1,a4,4(f5.3,2x),a1,/)')
$ 'seq',j,' = (',(z(j,i),i=1,len),')'
end do
end
my_system% f95 vsinq.f -xlic_lib=sunperf
my_system% a.out
Input sequences of length 4
seq1 = (0.557 0.352 0.990 0.539 )
seq2 = (0.603 0.867 0.417 0.156 )
Forward fast sine transform for quarter-wave odd sequences
seq1 = (0.823 0.057 0.078 0.305 )
seq2 = (0.654 0.466 -.069 -.037 )
Inverse fast sine transform for quarter-wave odd sequences
(results are normalized)
seq1 = (0.557 0.352 0.990 0.539 )
seq2 = (0.603 0.867 0.417 0.156 )
|
Convolution and Correlation
Two applications of the FFT that are frequently encountered especially in the signal processing area are the discrete convolution and discrete correlation operations.
Convolution
Given two functions x(t) and y(t), the Fourier transform of the convolution of x(t) and y(t), denoted as x 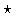 y, is the product of their individual Fourier transforms: DFT(x
y, is the product of their individual Fourier transforms: DFT(x 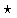 y)=X
y)=X Ywhere
Ywhere  denotes the convolution operation and
denotes the convolution operation and  denotes pointwise multiplication.
denotes pointwise multiplication.
Typically, x(t) is a continuous and periodic signal that is represented discretely by a set of N data points xj, j = 0, ..., N -1, sampled over a finite duration, usually for one period of x(t) at equal intervals. y(t) is usually a response that starts out as zero, peaks to a maximum value, and then returns to zero. Discretizing y(t) at equal intervals produces a set of N data points, yk, k = 0, ..., N -1. If the actual number of samplings in yk is less than N, the data can be padded with zeros. The discrete convolution can then be defined as
(x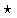 y)j
y)j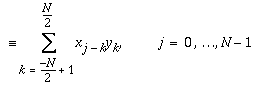 .
.
The values of  , are the same as those of
, are the same as those of 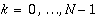 but in the wrap-around order.
but in the wrap-around order.
The Sun Performance Library routines allow the user to compute the convolution by using the definition above with k = 0, ..., N -1, or by using the FFT. If the FFT is used to compute the convolution of two sequences, the following steps are performed:
- Compute X = forward FFT of x
- Compute Y = forward FFT of y
- Compute z= inverse FFT of Z; z = (x
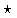 y)
y)
One interesting characteristic of convolution is that the product of two polynomials is actually a convolution. A product of an m-term polynomial
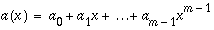
and an n-term polynomial
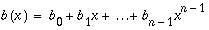
has m + n - 1 coefficients that can be obtained by
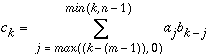 ,
,
where k = 0, ..., m + n - 2.
Correlation
Closely related to convolution is the correlation operation. It computes the correlation of two sequences directly superposed or when one is shifted relative to the other. As with convolution, we can compute the correlation of two sequences efficiently as follows using the FFT:
- Compute the FFT of the two input sequences.
- Compute the pointwise product of the resulting transform of one sequence and the complex conjugate of the transform of the other sequence.
- Compute the inverse FFT of the product.
The routines in the Performance Library also allow correlation to be computed by the following definition:
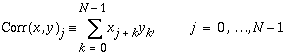 .
.
There are various ways to interpret the sampled input data of the convolution and correlation operations. The argument list of the convolution and correlation routines contain parameters to handle cases in which
- The signal and/or response function can start at different sampling time
- The user might want only part of the signal to contribute to the output
- The signal and/or response function can begin with one or more zeros that are not explicitly stored.
Sun Performance Library Convolution and Correlation Routines
Sun Performance Library contains the convolution routines shown in TABLE 6-6.
TABLE 6-6 Convolution and Correlation Routines
|
Routine
|
Arguments
|
Function
|
|
SCNVCOR, DCNVCOR, CCNVCOR, ZCNVCOR
|
CNVCOR,FOUR,NX,X,IFX,
INCX,NY,NPRE,M,Y,IFY,
INC1Y,INC2Y,NZ,K,Z,
IFZ,INC1Z,INC2Z,WORK,
LWORK
|
Convolution or correlation of a filter with one or more vectors
|
|
SCNVCOR2, DCNVCOR2, CCNVCOR2, ZCNVCOR2
|
CNVCOR,METHOD,TRANSX,
SCRATCHX,TRANSY,
SCRATCHY,MX,NX,X,LDX,
MY,NY,MPRE,NPRE,Y,LDY,
MZ,NZ,Z,LDZ,WORKIN,
LWORK
|
Two-dimensional convolution or correlation of two matrices
|
|
SWIENER, DWIENER
|
N_POINTS,ACOR,XCOR,
FLTR,EROP,ISW,IERR
|
Wiener deconvolution of two signals
|
The [S,D,C,Z]CNVCOR routines are used to compute the convolution or correlation of a filter with one or more input vectors. The [S,D,C,Z]CNVCOR2 routines are used to compute the two-dimensional convolution or correlation of two matrices.
Arguments for Convolution and Correlation Routines
The one-dimensional convolution and correlation routines use the arguments shown in TABLE 6-7.
TABLE 6-7 Arguments for One-Dimensional Convolution and Correlation Routines SCNVCOR , DCNVCOR , CCNVCOR , and ZCNVCOR
|
Argument
|
Definition
|
|
CNVCOR
|
`V' or `v' specifies that convolution is computed.
`R' or `r' specifies that correlation is computed.
|
|
FOUR
|
`T' or `t' specifies that the Fourier transform method is used.
`D' or `d' specifies that the direct method is used, where the convolution or correlation is computed from the definition of convolution and correlation.
|
|
NX
|
Length of filter vector, where NX  0. 0.
|
|
X
|
Filter vector
|
|
IFX
|
Index of first element of X, where NX  IFX IFX  1 1
|
|
INCX
|
Stride between elements of the vector in X, where INCX > 0.
|
|
NY
|
Length of input vectors, where NY  0. 0.
|
|
NPRE
|
Number of implicit zeros prefixed to the Y vectors, where NPRE  0. 0.
|
|
M
|
Number of input vectors, where M  0. 0.
|
|
Y
|
Input vectors.
|
|
IFY
|
Index of the first element of Y, where NY  IFY IFY  1 1
|
|
INC1Y
|
Stride between elements of the input vectors in Y, where INC1Y > 0.
|
|
INC2Y
|
Stride between input vectors in Y, where INC2Y > 0.
|
|
NZ
|
Length of the output vectors, where NZ  0. 0.
|
|
K
|
Number of Z vectors, where K  0. If K < M, only the first K vectors will be processed. If K > M, all input vectors will be processed and the last M-K output vectors will be set to zero on exit. 0. If K < M, only the first K vectors will be processed. If K > M, all input vectors will be processed and the last M-K output vectors will be set to zero on exit.
|
|
Z
|
Result vectors
|
|
IFZ
|
Index of the first element of Z, where NZ  IFZ IFZ  1 1
|
|
INC1Z
|
Stride between elements of the output vectors in Z, where INCYZ > 0.
|
|
INC2Z
|
Stride between output vectors in Z, where INC2Z > 0.
|
|
WORK
|
Work array
|
|
LWORK
|
Length of work array
|
The two-dimensional convolution and correlation routines use the arguments shown in TABLE 6-8.
TABLE 6-8 Arguments for Two-Dimensional Convolution and Correlation Routines SCNVCOR2 , DCNVCOR2 , CCNVCOR2 , and ZCNVCOR2
|
Argument
|
Definition
|
|
CNVCOR
|
`V' or `v' specifies that convolution is computed.
`R' or `r' specifies that correlation is computed.
|
|
METHOD
|
`T' or `t' specifies that the Fourier transform method is used.
`D' or `d' specifies that the direct method is used, where the convolution or correlation is computed from the definition of convolution and correlation.
|
|
TRANSX
|
`N' or `n' specifies that X is the filter matrix
`T' or `t' specifies that the transpose of X is the filter matrix
|
|
SCRATCHX
|
`N' or `n' specifies that X must be preserved
`S' or `s' specifies that X can be used for scratch space. The contents of X are undefined after returning from a call where X is used for scratch space.
|
|
TRANSY
|
`N' or `n' specifies that Y is the input matrix
`T' or `t' specifies that the transpose of Y is the input matrix
|
|
SCRATCHY
|
`N' or `n' specifies that Y must be preserved
`S' or `s' specifies that Y can be used for scratch space. The contents of X are undefined after returning from a call where Y is used for scratch space.
|
|
MX
|
Number of rows in the filter matrix X, where MX  0 0
|
|
NX
|
Number of columns in the filter matrix X, where NX  0 0
|
|
X
|
Filter matrix. X is unchanged on exit when SCRATCHX is `N' or `n' and undefined on exit when SCRATCHX is `S' or `s'.
|
|
LDX
|
Leading dimension of array containing the filter matrix X.
|
|
MY
|
Number of rows in the input matrix Y, where MY  0. 0.
|
|
NY
|
Number of columns in the input matrix Y, where NY  0 0
|
|
MPRE
|
Number of implicit zeros prefixed to each row of the input matrix Y vectors, where MPRE  0. 0.
|
|
NPRE
|
Number of implicit zeros prefixed to each column of the input matrix Y, where NPRE  0. 0.
|
|
Y
|
Input matrix. Y is unchanged on exit when SCRATCHY is `N' or `n' and undefined on exit when SCRATCHY is `S' or `s'.
|
|
LDY
|
Leading dimension of array containing the input matrix Y.
|
|
MZ
|
Number of output vectors, where MZ  0. 0.
|
|
NZ
|
Length of output vectors, where NZ  0. 0.
|
|
Z
|
Result vectors
|
|
LDZ
|
Leading dimension of the array containing the result matrix Z, where LDZ  MAX(1,MZ). MAX(1,MZ).
|
|
WORKIN
|
Work array
|
|
LWORK
|
Length of work array
|
Work Array WORK for Convolution and Correlation Routines
The minimum dimensions for the WORK work arrays used with the one-dimensional and two-dimensional convolution and correlation routines are shown in TABLE 6-11. The minimum dimensions for one-dimensional convolution and correlation routines depend upon the values of the arguments NPRE, NX, NY, and NZ.
The minimum dimensions for two-dimensional convolution and correlation routines depend upon the values of the arguments shown TABLE 6-9.
TABLE 6-9 Arguments Affecting Minimum Work Array Size for Two-Dimensional Routines: SCNVCOR2 , DCNVCOR2 , CCNVCOR2 , and ZCNVCOR2
|
Argument
|
Definition
|
|
MX
|
Number of rows in the filter matrix
|
|
MY
|
Number of rows in the input matrix
|
|
MZ
|
Number of output vectors
|
|
NX
|
Number of columns in the filter matrix
|
|
NY
|
Number of columns in the input matrix
|
|
NZ
|
Length of output vectors
|
|
MPRE
|
Number of implicit zeros prefixed to each row of the input matrix
|
|
NPRE
|
Number of implicit zeros prefixed to each column of the input matrix
|
|
MPOST
|
MAX(0,MZ-MYC)
|
|
NPOST
|
MAX(0,NZ-NYC)
|
|
MYC
|
MPRE + MPOST + MYC_INIT, where MYC_INIT depends upon filter and input matrices, as shown in TABLE 6-10
|
|
NYC
|
NPRE + NPOST + NYC_INIT, where NYC_INIT depends upon filter and input matrices, as shown in TABLE 6-10
|
MYC_INIT and NYC_INIT depend upon the following, where X is the filter matrix and Y is the input matrix.
TABLE 6-10 MYC_INIT and NYC_INIT Dependencies
|
|
Y
|
Transpose(Y)
|
|
|
X
|
Transpose(X)
|
X
|
Transpose(X)
|
|
MYC_INIT
|
MAX(MX,MY)
|
MAX(NX,MY)
|
MAX(MX,NY)
|
MAX(NX,NY)
|
|
NYC_INIT
|
MAX(NX,NY)
|
MAX(MX,NY)
|
MAX(NX,MY)
|
MAX(MX,MY)
|
The values assigned to the minimum work array size is shown in TABLE 6-11.
TABLE 6-11 Minimum Dimensions and Data Types for WORK Work Array Used With Convolution and Correlation Routines
|
Routine
|
Minimum Work Array Size (WORK)
|
Type
|
|
SCNVCOR, DCNVCOR
|
4*(MAX(NX,NPRE+NY) +
MAX(0,NZ-NY))
|
REAL, REAL*8
|
|
CCNVCOR, ZCNVCOR
|
2*(MAX(NX,NPRE+NY) +
MAX(0,NZ-NY)))
|
COMPLEX, COMPLEX*16
|
|
SCNVCOR2, DCNVCOR21
|
MY + NY + 30
|
COMPLEX, COMPLEX*16
|
|
CCNVCOR21, ZCNVCOR21
|
If MY = NY: MYC + 8
If MY  NY: MYC + NYC + 16 NY: MYC + NYC + 16
|
COMPLEX, COMPLEX*16
|
Sample Program: Convolution
CODE EXAMPLE 6-10 uses CCNVCOR to perform FFT convolution of two complex vectors.
CODE EXAMPLE 6-10 One-Dimensional Convolution Using Fourier Transform Method and COMPLEX Data
my_system% cat con_ex20.f
PROGRAM TEST
C
INTEGER LWORK
INTEGER N
PARAMETER (N = 3)
PARAMETER (LWORK = 4 * N + 15)
COMPLEX P1(N), P2(N), P3(2*N-1), WORK(LWORK)
DATA P1 / 1, 2, 3 /, P2 / 4, 5, 6 /
C
EXTERNAL CCNVCOR
C
PRINT *, 'P1:'
PRINT 1000, P1
PRINT *, 'P2:'
PRINT 1000, P2
CALL CCNVCOR ('V', 'T', N, P1, 1, 1, N, 0, 1, P2, 1, 1, 1,
$ 2 * N - 1, 1, P3, 1, 1, 1, WORK, LWORK)
C
PRINT *, 'P3:'
PRINT 1000, P3
C
1000 FORMAT (1X, 100(F4.1,' +',F4.1,'i '))
C
END
my_system% f95 -dalign con_ex20.f -xlic_lib=sunperf
my_system% a.out
P1:
1.0 + 0.0i 2.0 + 0.0i 3.0 + 0.0i
P2:
4.0 + 0.0i 5.0 + 0.0i 6.0 + 0.0i
P3:
4.0 + 0.0i 13.0 + 0.0i 28.0 + 0.0i 27.0 + 0.0i 18.0 + 0.0i
|
If any vector overlaps a writable vector, either because of argument aliasing or ill-chosen values of the various INC arguments, the results are undefined and can vary from one run to the next.
The most common form of the computation, and the case that executes fastest, is applying a filter vector X to a series of vectors stored in the columns of Y with the result placed into the columns of Z. In that case, INCX = 1, INC1Y = 1, INC2Y  NY, INC1Z = 1, INC2Z
NY, INC1Z = 1, INC2Z  NZ. Another common form is applying a filter vector X to a series of vectors stored in the rows of Y and store the result in the row of Z, in which case INCX = 1, INC1Y
NZ. Another common form is applying a filter vector X to a series of vectors stored in the rows of Y and store the result in the row of Z, in which case INCX = 1, INC1Y  NY, INC2Y = 1, INC1Z
NY, INC2Y = 1, INC1Z  NZ, and INC2Z = 1.
NZ, and INC2Z = 1.
Convolution can be used to compute the products of polynomials. CODE EXAMPLE 6-11 uses SCNVCOR to compute the product of 1 + 2x + 3x2 and 4 + 5x + 6x2.
CODE EXAMPLE 6-11 One-Dimensional Convolution Using Fourier Transform Method and REAL Data
my_system% cat con_ex21.f
PROGRAM TEST
INTEGER LWORK, NX, NY, NZ
PARAMETER (NX = 3)
PARAMETER (NY = NX)
PARAMETER (NZ = 2*NY-1)
PARAMETER (LWORK = 4*NZ+32)
REAL X(NX), Y(NY), Z(NZ), WORK(LWORK)
C
DATA X / 1, 2, 3 /, Y / 4, 5, 6 /, WORK / LWORK*0 /
C
PRINT 1000, 'X'
PRINT 1010, X
PRINT 1000, 'Y'
PRINT 1010, Y
CALL SCNVCOR ('V', 'T', NX, X, 1, 1,
$NY, 0, 1, Y, 1, 1, 1, NZ, 1, Z, 1, 1, 1, WORK, LWORK)
PRINT 1020, 'Z'
PRINT 1010, Z
1000 FORMAT (1X, 'Input vector ', A1)
1010 FORMAT (1X, 300F5.0)
1020 FORMAT (1X, 'Output vector ', A1)
END
my_system% f95 -dalign con_ex21.f -xlic_lib=sunperf
my_system% a.out
Input vector X
1. 2. 3.
Input vector Y
4. 5. 6.
Output vector Z
4. 13. 28. 27. 18.
|
Making the output vector longer than the input vectors, as in the example above, implicitly adds zeros to the end of the input. No zeros are actually required in any of the vectors, and none are used in the example, but the padding provided by the implied zeros has the effect of an end-off shift rather than an end-around shift of the input vectors.
CODE EXAMPLE 6-12 will compute the product between the vector [ 1, 2, 3 ] and the circulant matrix defined by the initial column vector [ 4, 5, 6 ].
CODE EXAMPLE 6-12 Convolution Used to Compute the Product of a Vector and Circulant Matrix
my_system% cat con_ex22.f
PROGRAM TEST
C
INTEGER LWORK, NX, NY, NZ
PARAMETER (NX = 3)
PARAMETER (NY = NX)
PARAMETER (NZ = NY)
PARAMETER (LWORK = 4*NZ+32)
REAL X(NX), Y(NY), Z(NZ), WORK(LWORK)
C
DATA X / 1, 2, 3 /, Y / 4, 5, 6 /, WORK / LWORK*0 /
C
PRINT 1000, 'X'
PRINT 1010, X
PRINT 1000, 'Y'
PRINT 1010, Y
CALL SCNVCOR ('V', 'T', NX, X, 1, 1,
$NY, 0, 1, Y, 1, 1, 1, NZ, 1, Z, 1, 1, 1,
$WORK, LWORK)
PRINT 1020, 'Z'
PRINT 1010, Z
C
1000 FORMAT (1X, 'Input vector ', A1)
1010 FORMAT (1X, 300F5.0)
1020 FORMAT (1X, 'Output vector ', A1)
END
my_system% f95 -dalign con_ex22.f -xlic_lib=sunperf
my_system% a.out
Input vector X
1. 2. 3.
Input vector Y
4. 5. 6.
Output vector Z
31. 31. 28.
|
The difference between this example and the previous example is that the length of the output vector is the same as the length of the input vectors, so there are no implied zeros on the end of the input vectors. With no implied zeros to shift into, the effect of an end-off shift from the previous example does not occur and the end-around shift results in a circulant matrix product.
CODE EXAMPLE 6-13 Two-Dimensional Convolution Using Direct Method
my_system% cat con_ex23.f
PROGRAM TEST
C
INTEGER M, N
PARAMETER (M = 2)
PARAMETER (N = 3)
C
INTEGER I, J
COMPLEX P1(M,N), P2(M,N), P3(M,N)
DATA P1 / 1, -2, 3, -4, 5, -6 /, P2 / -1, 2, -3, 4, -5, 6 /
EXTERNAL CCNVCOR2
C
PRINT *, 'P1:'
PRINT 1000, ((P1(I,J), J = 1, N), I = 1, M)
PRINT *, 'P2:'
PRINT 1000, ((P2(I,J), J = 1, N), I = 1, M)
C
CALL CCNVCOR2 ('V', 'Direct', 'No Transpose X', 'No Overwrite X',
$ 'No Transpose Y', 'No Overwrite Y', M, N, P1, M,
$ M, N, 0, 0, P2, M, M, N, P3, M, 0, 0)
C
PRINT *, 'P3:'
PRINT 1000, ((P3(I,J), J = 1, N), I = 1, M)
C
1000 FORMAT (3(F5.1,' +',F5.1,'i '))
C
END
my_system% f95 -dalign con_ex23.f -xlic_lib=sunperf
my_system% a.out
P1:
1.0 + 0.0i 3.0 + 0.0i 5.0 + 0.0i
-2.0 + 0.0i -4.0 + 0.0i -6.0 + 0.0i
P2:
-1.0 + 0.0i -3.0 + 0.0i -5.0 + 0.0i
2.0 + 0.0i 4.0 + 0.0i 6.0 + 0.0i
P3:
-83.0 + 0.0i -83.0 + 0.0i -59.0 + 0.0i
80.0 + 0.0i 80.0 + 0.0i 56.0 + 0.0i
|
References
For additional information on the DFT or FFT, see the following sources.
Briggs, William L., and Henson, Van Emden. The DFT: An Owner's Manual for the Discrete Fourier Transform. Philadelphia, PA: SIAM, 1995.
Brigham, E. Oran. The Fast Fourier Transform and Its Applications. Upper Saddle River, NJ: Prentice Hall, 1988.
Chu, Eleanor, and George, Alan. Inside the FFT Black Box: Serial and Parallel Fast Fourier Transform Algorithms. Boca Raton, FL: CRC Press, 2000.
Press, William H., Teukolsky, Saul A., Vetterling, William T., and Flannery, Brian P. Numerical Recipes in C: The Art of Scientific Computing. 2 ed. Cambridge, United Kingdom: Cambridge University Press, 1992.
Ramirez, Robert W. The FFT: Fundamentals and Concepts. Englewood Cliffs, NJ: Prentice-Hall, Inc., 1985.
Swartzrauber, Paul N. Vectorizing the FFTs. In Rodrigue, Garry ed. Parallel Computations. New York: Academic Press, Inc., 1982.
Strang, Gilbert. Linear Algebra and Its Applications. 3 ed. Orlando, FL: Harcourt Brace & Company, 1988.
Van Loan, Charles. Computational Frameworks for the Fast Fourier Transform. Philadelphia, PA: SIAM, 1992.
Walker, James S. Fast Fourier Transforms. Boca Raton, FL: CRC Press, 1991.
 0.
0.
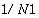 for one-dimensional transforms,
for one-dimensional transforms, 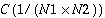 for two-dimensional transforms, and
for two-dimensional transforms, and 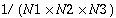 for three-dimensional transforms. In such case, the inverse transform is said to be normalized. If a normalized FFT is followed by its inverse FFT, the result is the original input data. The Sun Performance Library FFT routines are not normalized. However, normalization can be done easily by calling the inverse FFT routine with the appropriate scaling factor stored in SCALE.
for three-dimensional transforms. In such case, the inverse transform is said to be normalized. If a normalized FFT is followed by its inverse FFT, the result is the original input data. The Sun Performance Library FFT routines are not normalized. However, normalization can be done easily by calling the inverse FFT routine with the appropriate scaling factor stored in SCALE.
 , or expressed in polar form,
, or expressed in polar form,
 is also zero. Both zeros are stored explicitly. Because the second half of each sequence can be derived from the first half, only
is also zero. Both zeros are stored explicitly. Because the second half of each sequence can be derived from the first half, only  complex data points are computed and stored in the output array. Here and elsewhere in this chapter, integer division is rounded down.
complex data points are computed and stored in the output array. Here and elsewhere in this chapter, integer division is rounded down. complex data points of each conjugate symmetric input sequence are expected in the input, and the routine will return N1 real data points in each output sequence.
complex data points of each conjugate symmetric input sequence are expected in the input, and the routine will return N1 real data points in each output sequence.
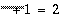 complex values are stored. For the in-place forward transform, SFFTCMis called with real array X as the input and output. Because SFFTCMexpects the output array to be of type COMPLEX, the leading dimension of X as an output array must be as if X were complex. Since the leading dimension of real array X is LDX= 2 ×LDC, the leading dimension of X as a complex output array must be LDC. Similarly, in the in-place inverse transform, CFFTSMis called with complex array Z as the input and output. Because CFFTSMexpects the output array to be of type REAL, the leading dimension of Z as an output array must be as if Z were real. Since the leading dimension of complex array Z is LDZ, the leading dimension of Z as a real output array must be LDZ×2.
complex values are stored. For the in-place forward transform, SFFTCMis called with real array X as the input and output. Because SFFTCMexpects the output array to be of type COMPLEX, the leading dimension of X as an output array must be as if X were complex. Since the leading dimension of real array X is LDX= 2 ×LDC, the leading dimension of X as a complex output array must be LDC. Similarly, in the in-place inverse transform, CFFTSMis called with complex array Z as the input and output. Because CFFTSMexpects the output array to be of type REAL, the leading dimension of Z as an output array must be as if Z were real. Since the leading dimension of complex array Z is LDZ, the leading dimension of Z as a real output array must be LDZ×2.
![(\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)X(\frac{N1}{2}+1:N1-1, [:)]X(0:\frac{N1}{2}, [:)] (\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)X(\frac{N1}{2}+1:N1-1, [:)]X(0:\frac{N1}{2}, [:)]](figures/plug_signal_proc-27.gif) . Conversely, when computing a complex-to-real transform (inverse FFT) of dimensions N1 ×N2, an
. Conversely, when computing a complex-to-real transform (inverse FFT) of dimensions N1 ×N2, an ![(\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)X(\frac{N1}{2}+1:N1-1, [:)]X(0:\frac{N1}{2}, [:)] (\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)X(\frac{N1}{2}+1:N1-1, [:)]X(0:\frac{N1}{2}, [:)]](figures/plug_signal_proc-28.gif) complex array is required as input. As with the real-to-complex and complex-to-real linear FFT, because of conjugate symmetry, only the first
complex array is required as input. As with the real-to-complex and complex-to-real linear FFT, because of conjugate symmetry, only the first ![(\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)X(\frac{N1}{2}+1:N1-1, [:)]X(0:\frac{N1}{2}, [:)] (\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)X(\frac{N1}{2}+1:N1-1, [:)]X(0:\frac{N1}{2}, [:)]](figures/plug_signal_proc-29.gif) complex data points need to be stored in the input or output array along the first dimension. The complex subarray
complex data points need to be stored in the input or output array along the first dimension. The complex subarray ![(\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)X(\frac{N1}{2}+1:N1-1, [:)]X(0:\frac{N1}{2}, [:)] (\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)X(\frac{N1}{2}+1:N1-1, [:)]X(0:\frac{N1}{2}, [:)]](figures/plug_signal_proc-30.gif) can be obtained from
can be obtained from ![(\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)X(\frac{N1}{2}+1:N1-1, [:)]X(0:\frac{N1}{2}, [:)] (\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)\times N2(\frac{N1}{2}+1)X(\frac{N1}{2}+1:N1-1, [:)]X(0:\frac{N1}{2}, [:)]](figures/plug_signal_proc-31.gif) as follows:
as follows: in the real-to-complex transform.
in the real-to-complex transform.
![(\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1) X(\frac{N1}{2}+1:N1-1,:, [:)]X(0:\frac{N1}{2},:, [:)] (\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1) X(\frac{N1}{2}+1:N1-1,:, [:)]X(0:\frac{N1}{2},:, [:)]](figures/plug_signal_proc-42.gif) . Conversely, when computing a complex-to-real FFT of dimensions N1 ×N2 ×N3, an
. Conversely, when computing a complex-to-real FFT of dimensions N1 ×N2 ×N3, an ![(\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1) X(\frac{N1}{2}+1:N1-1,:, [:)]X(0:\frac{N1}{2},:, [:)] (\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1) X(\frac{N1}{2}+1:N1-1,:, [:)]X(0:\frac{N1}{2},:, [:)]](figures/plug_signal_proc-43.gif) complex array is required as input. As with the real-to-complex and complex-to-real linear FFT, because of conjugate symmetry, only the first
complex array is required as input. As with the real-to-complex and complex-to-real linear FFT, because of conjugate symmetry, only the first ![(\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1) X(\frac{N1}{2}+1:N1-1,:, [:)]X(0:\frac{N1}{2},:, [:)] (\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1) X(\frac{N1}{2}+1:N1-1,:, [:)]X(0:\frac{N1}{2},:, [:)]](figures/plug_signal_proc-44.gif) complex data points need to be stored along the first dimension. The complex subarray
complex data points need to be stored along the first dimension. The complex subarray ![(\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1) X(\frac{N1}{2}+1:N1-1,:, [:)]X(0:\frac{N1}{2},:, [:)] (\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1) X(\frac{N1}{2}+1:N1-1,:, [:)]X(0:\frac{N1}{2},:, [:)]](figures/plug_signal_proc-45.gif) can be obtained from
can be obtained from ![(\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1) X(\frac{N1}{2}+1:N1-1,:, [:)]X(0:\frac{N1}{2},:, [:)] (\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1)\times N2\times N3(\frac{N1}{2}+1) X(\frac{N1}{2}+1:N1-1,:, [:)]X(0:\frac{N1}{2},:, [:)]](figures/plug_signal_proc-46.gif) as follows:
as follows: in the real-to-complex transform.
in the real-to-complex transform.
 complex data points. N1 real data points do map to N1 complex data points, but because there is conjugate symmetry in the complex data, only
complex data points. N1 real data points do map to N1 complex data points, but because there is conjugate symmetry in the complex data, only  data points need to be stored as input in the complex-to-real transform and as output in the real-to-complex transform. In the multi-dimensional FFT, symmetry exists along all the dimensions, not just in the first. However, the two-dimensional and three-dimensional FFT routines store the complex data of the second and third dimensions in their entirety.
data points need to be stored as input in the complex-to-real transform and as output in the real-to-complex transform. In the multi-dimensional FFT, symmetry exists along all the dimensions, not just in the first. However, the two-dimensional and three-dimensional FFT routines store the complex data of the second and third dimensions in their entirety. 0.
0.
 , the original sequences are obtained. An FCT of a real sequence of length 2Nthat has quarter-wave even symmetry requires Ninput data points and produces an N-point resulting sequence. Initialization is required before calling the transform routines by calling [V]COSQI.
, the original sequences are obtained. An FCT of a real sequence of length 2Nthat has quarter-wave even symmetry requires Ninput data points and produces an N-point resulting sequence. Initialization is required before calling the transform routines by calling [V]COSQI. .
.
 .
. .
.
 .
. y, is the product of their individual Fourier transforms: DFT(x
y, is the product of their individual Fourier transforms: DFT(x  y)=X
y)=X Ywhere
Ywhere  denotes the convolution operation and
denotes the convolution operation and  denotes pointwise multiplication.
denotes pointwise multiplication. , are the same as those of
, are the same as those of 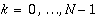 but in the wrap-around order.
but in the wrap-around order. NY, INC1Z = 1, INC2Z
NY, INC1Z = 1, INC2Z  NZ. Another common form is applying a filter vector X to a series of vectors stored in the rows of Y and store the result in the row of Z, in which case INCX = 1, INC1Y
NZ. Another common form is applying a filter vector X to a series of vectors stored in the rows of Y and store the result in the row of Z, in which case INCX = 1, INC1Y  NY, INC2Y = 1, INC1Z
NY, INC2Y = 1, INC1Z  NZ, and INC2Z = 1.
NZ, and INC2Z = 1.