| C H A P T E R 2 |
|
f95 Interval Reference |
This chapter is a reference for the syntax and semantics of the intrinsic INTERVAL types implemented in Sun Studio Fortran 95. The sections can be read in any order.
Unless explicitly stated otherwise, the INTERVAL data type has the same properties as other intrinsic numeric types. This chapter highlights differences between the REAL and INTERVAL types.
Some code examples are not complete programs. The implicit assumption is that these examples are compiled with the -xia command line option.
INTERVAL data types are a non-standard extension to Fortran. However, where possible, the implemented syntax and semantics conform to the style of Fortran.
Left and right square brackets, "[...]", are added to the Fortran character set to delimit literal INTERVAL constants.
Throughout this document, unless explicitly stated otherwise, INTEGER, REAL, and INTERVAL constants mean literal constants. Constant expressions and named constants (PARAMETERS) are always explicitly identified as such.
TABLE 2-1 shows the character set notation used for code and mathematics.
|
|
|
Note - Pay close attention to font usage. Different fonts represent an interval's exact, external mathematical value and an interval's machine-representable, internal approximation. |
In f95, an INTERVAL constant is either a single integer or real decimal number enclosed in square brackets, [3.5], or a pair of integer or real decimal numbers separated by a comma and enclosed in square brackets, [3.5 E-10, 3.6 E-10]. If a degenerate interval is not machine representable, directed rounding is used to round the exact mathematical value to an internal machine representable interval known to satisfy the containment constraint.
An INTERVAL constant with both endpoints of type default INTEGER, default REAL or REAL(8), has the default type INTERVAL.
If an endpoint is of type default INTEGER, default REAL or REAL(8), it is internally converted to a value of the type REAL(8).
If an endpoint's type is INTEGER(8), it is internally converted to a value of type REAL(16).
If an endpoint's type is INTEGER(4), it is internally converted to a value of type REAL(8).
If an endpoint's type is INTEGER(1) or INTEGER(2), it is internally converted to a value of type REAL(4).
If both endpoints are of type REAL but have different KTPVs, they are both internally represented using the approximation method of the endpoint with greater decimal precision.
The KTPV of an INTERVAL constant is the KTPV of the part with the greatest decimal precision.
CODE EXAMPLE 2-1 shows the KTPV of various INTERVAL constants.
A Fortran constant, such as 0.1 or [0.1,0.2], is associated with the two values: the external value it represents and its internal approximation. In Fortran, the value of a constant is its internal approximation. There is no need to distinguish between a constant's external value and its internal approximation. Intervals require this distinction to be made. To represent a Fortran constant's external value, the following notation is used:
ev(0.1) = 0.1 or ev([0.1,0.2])= [0.1, 0.2].
The notation ev stands for external value.
Following the Fortran Standard, the numerical value of an INTERVAL constant is its internal approximation. The external value of an INTERVAL constant is always explicitly labelled as such.
For example, the INTERVAL constant [1, 2] and its external value ev([1, 2]) are equal to the mathematical value [1, 2]. However, while ev([0.1, 0.2]) = [0.1, 0.2], [0.1, 0.2] is only an internal machine approximation, because the numbers 0.1 and 0.2 are not machine representable. The value of the INTERVAL constant, [0.1, 0.2] is its internal machine approximation. The external value is denoted ev([0.1, 0.2]).
Under strict expression processing, an INTERVAL constant's internal approximation is fixed, as it is for other Fortran numeric typed constants. The value of a REAL constant is its internal approximation. Similarly, the value of an INTERVAL constant's internal approximation is referred to as the constant's value. A constant's external value, which is not a defined concept in standard Fortran, can be different from its internal approximation. Under widest-need expression processing, an INTERVAL constant's internal value is context-dependent. Nevertheless, an INTERVAL constant's internal approximation must contain its external value in both strict and widest-need expression processing.
Like any mathematical constant, the external value of an INTERVAL constant is invariant. The external value of a named INTERVAL constant (PARAMETER) cannot change within a program unit. However, as with any named constant, in different program units, different values can be associated with the same named constant.
Because intervals are opaque, there is no language requirement to store the information needed to internally represent an interval. Intrinsic functions are provided to access the infimum and supremum of an interval. Nevertheless, an INTERVAL constant is defined by an ordered pair of REAL or INTEGER constants. The constants are separated by a comma, and the pair is enclosed in square brackets. The first constant is the infimum or lower bound, and the second, is the supremum or upper bound.
If only one constant appears inside the square brackets, the represented interval is degenerate, having equal infimum and supremum. In this case, an internal interval approximation is constructed that is guaranteed to contain the single decimal literal constant's external value.
A valid interval must have an infimum that is less than or equal to its supremum. Similarly, an INTERVAL constant must also have an infimum that is less than or equal to its supremum. For example, the following code fragment must evaluate to true:
CODE EXAMPLE 2-2 contains examples of valid and invalid INTERVAL constants.
For additional information regarding INTERVAL constants, see the supplementary paper [4] cited in Section 2.11, References.
The internal approximation of a REAL constant does not necessarily equal the constant's external value. For example, because the decimal number 0.1 is not a member of the set of binary floating-point numbers, this value can only be approximated by a binary floating-point number that is close to 0.1. For REAL data items, the approximation accuracy is unspecified in the Fortran standard. For INTERVAL data items, a pair of floating-point values is used that is known to contain the set of mathematical values defined by the decimal numbers used to symbolically represent an INTERVAL constant. For example, the mathematical interval [0.1, 0.2] is the external value of the INTERVAL constant [0.1,0.2].
Just as there is no Fortran language requirement to accurately approximate REAL constants, there is also no language requirement to approximate an interval's external value with a narrow width INTERVAL constant. There is a requirement for an INTERVAL constant to contain its external value.
ev(INF([0.1,0.2])) 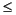 inf(ev([0.1,0.2])) = inf([0.1, 0.2])
inf(ev([0.1,0.2])) = inf([0.1, 0.2])
sup([0.1, 0.2]) = sup(ev([0.1,0.2])) 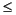 ev(SUP([0.1,0.2]))
ev(SUP([0.1,0.2]))
f95 INTERVAL constants are sharp. This is a quality of implementation feature.
The INTERVAL declaration statement is the only INTERVAL-specific statement added to the Fortran language in f95. For a detailed description of the INTERVAL declaration statement and standard Fortran statements that interact with INTERVAL data items, see Section 2.10, INTERVAL Statements.
If the -xia or -xinterval options are entered in the f95 command line, or if they are set either to widestneed or to strict, the INTERVAL data type is recognized as an intrinsic numeric data type in f95. If neither option is entered in the f95 command line, or if they are set to no, the INTERVAL data type is not recognized as intrinsic. See Section 2.3.3, Interval Command-Line Options for details on the INTERVAL command-line options.
The intrinsic type INTERVAL is added to the six intrinsic Fortran data types. The INTERVAL type is opaque, meaning that an INTERVAL data item's internal format is not specified. Nevertheless, an INTERVAL data item's external format is a pair of REAL data items having the same kind type parameter value (KTPV) as the INTERVAL data item.
An INTERVAL data item is an approximation of a mathematical interval consisting of a lower bound or infimum and an upper bound or supremum. INTERVAL data items have all the properties of other numeric data items.
The KTPV of a default INTERVAL data item is 8. The size of a default INTERVAL data item with no specified KTPV is 16 bytes. The size of a default INTERVAL data item in f95 cannot be changed using the -xtypemap or -r8const command line options. For more information, see Section 2.3.3.1, -xtypemap and -r8const Command-Line Options. Thus
KIND([0])= 2*KIND(0) = KIND(0.0_8) = 8
provided the size of the default REAL and INTEGER data items is not changed using -xtypemap.
The size and alignment of INTERVAL types is unaffected by f95 compiler options. TABLE 2-2 contains INTERVAL sizes and alignments.
INTERVAL arrays have all the properties of arrays with different numeric types. See CODE EXAMPLE 2-25 for the declaration of INTERVAL arrays.
Interval versions of the following intrinsic array functions are supported:
ALLOCATED(), ASSOCIATED(), CSHIFT(), DOT_PRODUCT(), EOSHIFT(), KIND(), LBOUND(), MATMUL(), MAXVAL(), MERGE(), MINVAL(), NULL(), PACK(), PRODUCT(), RESHAPE(), SHAPE(), SIZE(), SPREAD(), SUM(), TRANSPOSE(), UBOUND(), UNPACK().
The MINLOC(), and MAXLOC() intrinsic functions are not defined for INTERVAL arrays because the MINVAL and MAXVAL intrinsic applied to an INTERVAL array might return an interval value not possessed by any element of the array. See the following sections for descriptions of the MAX and MIN intrinsic functions:
For example MINVAL((/[1,2],[3,4]/)) = [1,3] and
MAXVAL(/[1,2],[3,4]/) = [2,4].
Array versions of the following intrinsic INTERVAL-specific functions are supported: ABS(), INF(), MAG(), MAX(), MID(), MIG(), MIN(), NDIGITS(), SUP(), WID().
Array versions of the following intrinsic INTERVAL-mathematical functions are supported: ACOS(), AINT(), ANINT(), ASIN(), ATAN(), ATAN2(), CEILING(), COS(), COSH(), EXP(), FLOOR(), LOG(), LOG10(), MOD(), SIGN(), SIN(), SINH(), SQRT(), TAN(), TANH().
Array versions of the following INTERVAL constructors are supported:
INTERVAL(), DINTERVAL(), SINTERVAL(), QINTERVAL().
INTERVAL arithmetic expressions are constructed from the same arithmetic operators as other numerical data types. The fundamental difference between INTERVAL and non-INTERVAL (point) expressions is that the result of any possible INTERVAL expression is a valid INTERVAL that satisfies the containment constraint of interval arithmetic. In contrast, point expression results can be any approximate value.
Mixed-mode (INTERVAL-point) expressions require widest-need expression processing to guarantee containment. Expression processing is widest-need by default when support for intervals is invoked using either the -xia command-line macro or the -xinterval command line option. If widest-need expression processing is not wanted, use the options -xia=strict or -xinterval=strict to invoke strict expression processing. Mixed-mode INTERVAL expressions are compile-time errors under strict expression processing. Mixed-mode operations between INTERVAL and COMPLEX operands are not supported.
With widest-need expression processing, the KTPV of all operands in an interval expression is promoted to KTPVmax, the highest INTERVAL KTPV found anywhere in the expression.
|
Note - KTPV promotion is performed before expression evaluation. |
Widest-need expression processing guarantees:
Each of the following examples is designed to illustrate the behavior and utility of widest-need expression processing. There are three blocks of code in each example:
The examples are designed to communicate three messages:
The INTERVAL assignment statement assigns a value of an INTERVAL scalar, array element, or array expression to an INTERVAL variable, array element or array. The syntax is:
where expr is a placeholder for an interval arithmetic or array expression, and V is an INTERVAL variable, array element, array, array section, or structure component.
Executing an INTERVAL assignment causes the expression to be evaluated using either widest-need or strict expression processing. The resulting value is then assigned to V. The following steps occur when evaluating an expression using widest-need expression processing:
1. The interval KTPV of every point (non-INTERVAL) data item is computed.
If the point item is an integer, the resulting interval KTPV is twice the integer's KTPV. Otherwise an interval's KTPV is the same as the point item's KTPV.
2. The expression, including the left-hand side of an assignment statement, is scanned for the maximum interval KTPV, denoted KTPVmax.
3. All point and INTERVAL data items in the INTERVAL expression are promoted to KTPVmax, prior to evaluating the expression.
4. If KIND(V) < KTPVmax after the expression is evaluated, the expression result is converted to a containing interval with KTPV = KIND(V) and the resulting value is assigned to V.
CODE EXAMPLE 2-4 notes:
Interval features in the f95 compiler are activated by means of the following command-line options:
-xia expands into the following.
-xinterval=widestneed
-ftrap=%none
-fns=no
-fsimple=0
-xia=(widestneed|strict) expands into the following.
-xinterval=(widestneed|strict)
-ftrap=%none
-fns=no
-fsimple=0
Previously set values of -ftrap, -fns, -fsimple are superseded.
It is a fatal error if at the end of command line processing -xinterval=(widestneed|strict) is set, and either -fsimple, -fns, or -ftrap is set to any value other than
-fsimple=0
-fns=no
-ftrap=no
-ftrap=%none
When using command-line options:
When recognition of INTERVAL types is activated:
The size of a default INTERVAL variable declared only with the INTERVAL keyword cannot be changed using the -xtypemap and -r8const command line options.
While these command line options have no influence on the size of default INTERVAL types, the options can change the result of mixed-mode INTERVAL expressions, as shown in CODE EXAMPLE 2-5.
|
Note - Although -xtypemap has no influence on the KTPV of X, it can influence the value of X. |
INTERVAL constant expressions may contain INTERVAL literal and named constants, as well as any point constant expression components. Therefore, each operand or argument is itself, another constant expression, a constant, a named constant, or an intrinsic function called with constant arguments.
|
Note - Under widest-need expression processing, interval context is used to determine the KTPV of INTERVAL constants. See Section 1.3.7, Default Kind Type Parameter Value (KTPV) for more information. |
INTERVAL constant expressions are permitted wherever an INTERVAL constant is allowed.
TABLE 2-3 lists the intrinsic operators that can be used with intervals. In TABLE 2-3, X and Y are intervals.
| (1) If N is an integer expression, overflow can cause a containment failure under -xia=strict expression processing. This is not a problem under widest-need expression processing. Users must be responsible for preventing integer overflow under strict expression processing. See Section 1.5.1.1, Integer Overflow for more information. | |||
|---|---|---|---|
With the exception of the interval ** operator and an integer exponent, interval operators can only be applied to two interval operands with the same kind type parameter value. Thus the type and KTPV of an interval operator's result are the same as the type and KTPV of its operands.
If the second operand of the interval ** operator is an integer, the first operand can be of any interval KTPV. In this case, the result has the type and KTPV of the first operand.
Some INTERVAL-specific operators have no point analogs. These can be grouped into three categories: set, certainly, and possibly, as shown in TABLE 2-4. A number of unique set-operators have no certainly or possibly analogs.
The precedence of intrinsic INTERVAL relational operators is the same as the precedence of REAL relational operators.
Except for the .IN. operator, intrinsic INTERVAL relational operators can only be applied to two INTERVAL operands with the same KTPV.
The first operand of the .IN. operator is of any INTEGER or REAL type. The second operand can have any interval KTPV.
The result of the INTERVAL relational expression has the default LOGICAL kind type parameter.
Formulas for computing the endpoints of interval arithmetic operations on finite REAL intervals are motivated by the requirement to produce the narrowest interval that is guaranteed to contain the set of all possible point results. Ramon Moore independently developed these formulas and more importantly, was the first to develop the analysis needed to apply interval arithmetic. For more information, see R. Moore, Interval Analysis, Prentice-Hall, 1966.
The set of all possible values was originally defined by performing the operation in question on any element of the operand intervals. Therefore, given finite intervals, [a, b] and [c, d], with 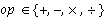 ,
,
with division by zero being excluded. The formulas, or their logical equivalent, are:
Directed rounding is used when computing with finite precision arithmetic to guarantee the set of all possible values is contained in the resulting interval.
The set of values that any interval result must contain is called the containment set (cset) of the operation or expression that produces the result.
To include extended intervals (with infinite endpoints) and division by zero, csets can only indirectly depend on the value of arithmetic operations on real operands. For extended intervals, csets are required for operations on points that are normally undefined. Undefined operations include the indeterminate forms: 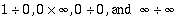 .
.
The containment-set closure identity solves the problem of identifying the value of containment sets of expressions at singular or indeterminate points. The identity states that containment sets are function closures. The closure of a function at a point on the boundary of its domain includes all limit or accumulation points. For details, see the Glossary and the supplementary papers [1], [3], [10], and [11] cited in Section 2.11, References.
The following is an intuitive way to justify the values included in an expression's cset. Consider the function
The question is: What is the cset of h(x0), for x0 = 0 ? To answer this question, consider the function
Clearly, f(x0) = 0, for x0 = 0. But, what about
The function g(x0) is undefined for x0 = 0, because h(x0) is undefined. The cset of h(x0) for x0 = 0 is the smallest set of values for which g(x0) = f(x0). Moreover, this must be true for all composite functions of h. For example if
then g(x) = g'(h(x)). In this case, it can be proved that the cset of h(x0) = 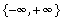 if x0= 0, where
if x0= 0, where 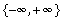 denotes the setconsisting of the two values,
denotes the setconsisting of the two values, 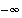 and
and 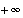 .
.
TABLE 2-5 through TABLE 2-8, contain the csets for the basic arithmetic operations. It is convenient to adopt the notation that an expression denoted by f(x) simply means its cset. Similarly, if
the containment set of f over the interval X, then hull(f(x)) is the sharp interval that contains f(X).
|
|
|||
|
|
|
|
|||
|
|
|
|
|||||
|
|
|
||||
|
|
|
|
|||||
All inputs in the tables are shown as sets. Results are shown as sets or intervals. Customary notation, such as 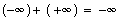 ,
, 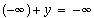 , and
, and 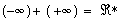 , is used, with the understanding that csets are implied when needed. Results for general set (or interval) inputs are the union of the results of the single-point results as they range over the input sets (or intervals).
, is used, with the understanding that csets are implied when needed. Results for general set (or interval) inputs are the union of the results of the single-point results as they range over the input sets (or intervals).
In one case, division by zero, the result is not an interval, but the set, ![{-inf, +inf}[-inf, +inf]=R* {-inf, +inf}[-inf, +inf]=R*](figures/iapgFreference-35.gif) . In this case, the narrowest interval in the current system that does not violate the containment constraint of interval arithmetic is the interval
. In this case, the narrowest interval in the current system that does not violate the containment constraint of interval arithmetic is the interval ![{-inf, +inf}[-inf, +inf]=R* {-inf, +inf}[-inf, +inf]=R*](figures/iapgFreference-36.gif) .
.
Sign changes produce the expected results.
To incorporate these results into the formulas for computing interval endpoints, it is only necessary to identify the desired endpoint, which is also encoded in the rounding direction. Using 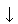 to denote rounding down (towards -
to denote rounding down (towards -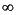 ) and
) and 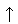 to denote rounding up (towards +
to denote rounding up (towards +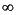 ),
),
Finally, the empty interval is represented in Fortran by the character string [empty] and has the same properties as the empty set, denoted 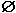 in the algebra of sets. Any arithmetic operation on an empty interval produces an empty interval result. For additional information regarding the use of empty intervals, see the supplementary papers [6] and [7] cited in Section 2.11, References.
in the algebra of sets. Any arithmetic operation on an empty interval produces an empty interval result. For additional information regarding the use of empty intervals, see the supplementary papers [6] and [7] cited in Section 2.11, References.
Using these results, f95 implements the "simple" closed interval system. The system is closed because all arithmetic operations and functions always produce valid interval results. See the supplementary papers [2] and [8] cited in Section 2.11, References.
The power operator can be used with integer exponents (X**N) and continuous exponents (X**Y). With a continuous exponent, the power operator has indeterminate forms, similar to the four arithmetic operators.
In the integer exponents case, the set of all values that an enclosure of 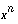 must contain is
must contain is 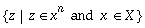 .
.
Monotonicity can be used to construct a sharp interval enclosure of the integer power function. When n= 0, Xn, which represents the cset of Xn,is 1 for all ![x is an element of [-inf, +inf]empty^n = empty x is an element of [-inf, +inf]empty^n = empty](figures/iapgFreference-54.gif) , and
, and ![x is an element of [-inf, +inf]empty^n = empty x is an element of [-inf, +inf]empty^n = empty](figures/iapgFreference-55.gif) for all n.
for all n.
In the continuous exponents case, the set of all values that an interval enclosure of X**Y must contain is

where 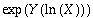 and exp(y(ln(x))) are their respective containment sets. The function exp(y(ln(x))) makes explicit that only values of x
and exp(y(ln(x))) are their respective containment sets. The function exp(y(ln(x))) makes explicit that only values of x 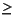 0 need be considered, and is consistent with the definition of X**Ywith REALarguments in Fortran.
0 need be considered, and is consistent with the definition of X**Ywith REALarguments in Fortran.
The result is empty if either INTERVAL argument is empty, or if x < 0. This is also consistent with the point version of X**Y in Fortran.
TABLE 2-9 displays the containment sets for all the singularities and indeterminate forms of exp(y(ln(x))).
The results in TABLE 2-9 can be obtained in two ways:
For most compositions, the second option is much easier. If sufficient conditions are satisfied, the closure of a composition can be computed from the composition of its closures. That is, the closure of each sub-expression can be used to compute the closure of the entire expression. In the present case,
exp(y(ln(x))) = exp(y0 × ln(x0)).
That is, the cset of the expression on the left is equal to the composition of csets on the right.
exp(y(ln(x))) 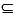 exp(y0 × ln(x0)).
exp(y0 × ln(x0)).
Note that this is exactly how interval arithmetic works on intervals. The needed closures of the ln and exp functions are:
 ln(0) = -inf, ln(+inf)=+inf, exp(-inf)=0, exp(+inf)=+inf
ln(0) = -inf, ln(+inf)=+inf, exp(-inf)=0, exp(+inf)=+inf
A necessary condition for closure-composition equality is that the expression must be a single-use expression (or SUE), which means that each independent variable can appear only once in the expression.
In the present case, the expression is clearly a SUE.
The entries in TABLE 2-9 follow directly from using the containment set of the basic multiply operation in TABLE 2-7 on the closures of the ln and exp functions. For example, with x0 = 1 and y0 = -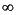 , ln(x0) = 0. For the closure of multiplication on the values -
, ln(x0) = 0. For the closure of multiplication on the values -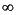 and 0 in TABLE 2-7, the result is [-
and 0 in TABLE 2-7, the result is [-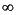 , +
, + ]. Finally, exp([-
]. Finally, exp([-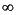 , +
, +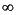 ]) = [0, +
]) = [0, +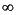 ], the second entry in TABLE 2-9. Remaining entries are obtained using the same steps. These same results are obtained from the direct derivation of the containment set of exp(y(ln(x))). At this time, sufficient conditions for closure-composition equality of any expression have not been identified. Nevertheless,
], the second entry in TABLE 2-9. Remaining entries are obtained using the same steps. These same results are obtained from the direct derivation of the containment set of exp(y(ln(x))). At this time, sufficient conditions for closure-composition equality of any expression have not been identified. Nevertheless,
The dependent subtraction operator .DSUB. can be used to recover either operand of a previous interval addition.
Two interval variables are dependent when one interval variable is a result of an interval arithmetic operation applied to the other interval variable. For example, if X = A + B, then X depends on both A and B. Dependent interval subtraction produces narrower interval results when recovering A or B from X.
Dependent operations cannot be applied to interval constants because interval constants are not the result of an interval operation, and therefore, cannot be dependent. Applying dependent operations to interval constants produces a compile-time error.
The result of X.DSUB.A returns an enclosure of B given that X = A + B, as shown in TABLE 2-10.
|
Finite interval[1] |
|||
f95 supports the following set theoretic operators for determining the interval hull and intersection of two intervals.
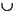 Y or (X.IH.Y)
Y or (X.IH.Y)Description: Interval hull of two intervals. The interval hull is the smallest interval that contains all the elements of the operand intervals.
Mathematical and operational definitions:
Arguments: X and Y must be intervals with the same KTPV.
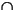 Y or (X.IX.Y)
Y or (X.IX.Y)Description: Intersection of two intervals.
Mathematical and operational definitions:
Arguments: X and Y must be intervals with the same KTPV.
f95 provides the following set relations that have been extended to support intervals.
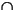 Y =
Y = 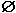 or (X .DJ. Y)
or (X .DJ. Y) Description: Test if two intervals are disjoint.
Mathematical and operational definitions:
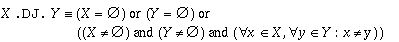
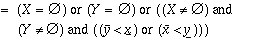
Arguments: X and Y must be intervals with the same KTPV.
Result type: Default logical scalar.
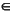 Y or (R.IN. Y)
Y or (R.IN. Y)Description: Test if the number, R, is an element of the interval, Y.
Mathematical and operational definitions:
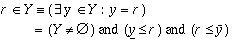
Arguments: The type of R is INTEGER or REAL, and the type of Y is INTERVAL.
Result type: Default logical scalar.
The following comments refer to the 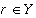 set relation:
set relation:
Description: Test if X is in interior of Y.
The interior of a set in topological space is the union of all open subsets of the set.
For intervals, the relation X .INT. Y (X in interior of Y) means that X is a subset of Y, and both of the following relations are false:
Note also that, 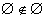 , but [empty].INT.[empty]= true
, but [empty].INT.[empty]= true
The empty set is open and therefore is a subset of the interior of itself.
Mathematical and operational definitions:
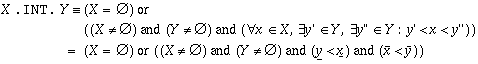
Arguments: X and Y must be intervals with the same KTPV.
Result type: Default logical scalar.
 Y or (X .PSB. Y)
Y or (X .PSB. Y) Description: Test if X is a proper subset of Y
Mathematical and operational definitions:
Arguments: X and Y must be intervals with the same KTPV.
Result type: Default logical scalar.
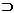 Y or (X .PSP. Y)
Y or (X .PSP. Y)Description:Seeproper subset with 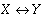 .
.
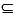 Y or (X .SB. Y)
Y or (X .SB. Y)Description: Test if X is a subset of Y
Mathematical and operational definitions:
Arguments: X and Y must be intervals with the same KTPV.
Result type: Default logical scalar.
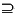 Y or (X .SP. Y)
Y or (X .SP. Y)An intrinsic INTERVAL relational operator, denoted .qop., is composed by concatenating:
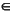 {C,P,S}, where C, P, and S stand for certainly, possibly, and set, respectively
{C,P,S}, where C, P, and S stand for certainly, possibly, and set, respectively
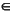 {LT, LE, EQ, NE, GT, GE}
{LT, LE, EQ, NE, GT, GE}
In place of .SEQ. and .SNE., .EQ. (or ==) and .NE. (or /=) defaults are accepted. To eliminate code ambiguity, all other INTERVAL relational operators must be made explicit by specifying a prefix.
All INTERVAL relational operators have equal precedence. Arithmetic operators have higher precedence than relational operators.
INTERVAL relational expressions are evaluated by first evaluating the two operands, after which the two expression values are compared. If the specified relationship holds, the result value is true; otherwise, it is false.
When widest-need expression processing is invoked, it applies to both INTERVAL operand expressions of INTERVAL relational operators.
Letting "nop" stand for the complement of the operator op, the certainly and possibly operators are related as follows:
Assuming neither operand is empty, TABLE 2-11 contains the Fortran operational definitions of all INTERVAL relational operators of the form:
The first column contains the value of the prefix, and the first row contains the value of the operator suffix. If the tabled condition holds, the result is true.
CODE EXAMPLE 2-7 notes:
For an affirmative order relation with
between two points x and y, the mathematical definition of the corresponding set-relation, .Sop., between two non-empty intervals X and Y is:
For the relation 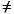 between two points x and y, the corresponding set relation, .SNE., between two non-empty intervals X and Y is:
between two points x and y, the corresponding set relation, .SNE., between two non-empty intervals X and Y is:
Empty intervals are explicitly considered in each of the following relations. In each case:
Arguments: X and Y must be intervals with the same KTPV.
Result type: default logical scalar.
Thecertainly relational operators are true if the underlying relation is true for every element of the operand intervals. For example, [a,b].CLT.[c,d]is true if x< yfor all ![x is an element of [a, b]y is an element of [c, d] x is an element of [a, b]y is an element of [c, d]](figures/iapgFreference-80.gif) and
and ![x is an element of [a, b]y is an element of [c, d] x is an element of [a, b]y is an element of [c, d]](figures/iapgFreference-81.gif) . This is equivalent to b< c.
. This is equivalent to b< c.
For an affirmative order relation with
between two points x and y, the corresponding certainly-true relation .Cop. between two intervals, X and Y, is
With the exception of the anti-affirmative certainly-not-equal relation, if either operand of a certainly relation is empty, the result is false. The one exception is the certainly-not-equal relation, .CNE., which is true in this case.
For each of the certainly relational operators:
Arguments: X and Y must be intervals with the same KTPV.
Result type: default logical scalar.
The possibly relational operators are true if any element of the operand intervals satisfy the underlying relation. For example, [a,b].PLT.[c,d]is true if there exists an ![x is an element of [a, b]y is an element of [c, d] x is an element of [a, b]y is an element of [c, d]](figures/iapgFreference-84.gif) and a
and a ![x is an element of [a, b]y is an element of [c, d] x is an element of [a, b]y is an element of [c, d]](figures/iapgFreference-85.gif) such that x< y. This is equivalent to a< d.
such that x< y. This is equivalent to a< d.
For an affirmative order relation with
between two points x and y, the corresponding possibly-true relation .Pop. between two intervals X and Y is defined as follows:
If the empty interval is an operand of a possibly relation then the result is false. The one exception is the anti-affirmative possibly-not-equal relation, .PNE., which is true in this case.
For each of the possibly relational operators:
Arguments: X and Y must be INTERVALS with the same KTPV.
Result type: default logical scalar.
If the operator specified in the INTERFACE statement of a user provided operator interface block is an intrinsic INTERVAL operator (for example .IH.), an extension to the intrinsic INTERVAL operator is created.
A user-provided operator function that extends an intrinsic INTERVAL operator may not extend the operator for those data types of its operands for which this operator is predefined.
For the combinations of arguments listed below, intrinsic interval operators +, -, *, /, .IH., .IX., and ** are predefined and cannot be extended by users.
(any INTERVAL type, any INTERVAL type)
(any INTERVAL type, any REAL or INTEGER type)
(any REAL or INTEGER type, any INTERVAL type)
The interval operator ** with the integer exponent is predefined and cannot be extended by users for the following combination of arguments:
(any INTERVAL type, any INTEGER type)
Except for the operator .IN. interval relational operators are predefined for the combinations of arguments listed below and cannot be extended by users.
(any INTERVAL type, any INTERVAL type)
(any INTERVAL type, any REAL or INTEGER type)
(any REAL or INTEGER type, any INTERVAL type)
The interval relational operator .IN. is predefined and cannot be extended by users for the following combination of arguments:
(any REAL or INTEGER type, any INTERVAL type)
In CODE EXAMPLE 2-8, both S1 and S2 interfaces are correct, because .IH. is not predefined for (LOGICAL, INTERVAL(16)) operands.
The extension of the + operator in CODE EXAMPLE 2-9 is incorrect because the attempt is made to change the definition of the intrinsic INTERVAL (+) operator, which is predefined for (INTERVAL, INTERVAL) type operands.
In CODE EXAMPLE 2-10, the following S1 interface is incorrect, because .IH. is predefined for (INTERVAL(4), INTERVAL(8)) operands.
The number of arguments of an operator function that extends an intrinsic INTERVAL operator must agree with the number of operands needed for the intrinsic operator, as shown in CODE EXAMPLE 2-11.
A binary intrinsic INTERVAL operator cannot be extended with unary operator function having an INTERVAL argument.
In CODE EXAMPLE 2-12, the S1 interface is incorrect, because "+" is predefined for the INTERVAL operand.
In a generic interface block, if the generic name specified in the INTERFACE statement is the name of an intrinsic INTERVAL subprogram, the specific user-defined subprograms extend the predefined meaning of the intrinsic subprogram.
All references to subprograms having the same generic name must be unambiguous.
The intrinsic subprogram is treated as a collection of specific intrinsic subprograms, the interface definitions of which are also specified in the generic interface block.
CODE EXAMPLE 2-14 is correct.
CODE EXAMPLE 2-15 is correct.
CODE EXAMPLE 2-16 illustrates how widest-need expression processing occurs when calling predefined versus extended versions of an intrinsic INTERVAL operator.
CODE EXAMPLE 2-17 illustrates how widest-need expression processing occurs when calling a user-defined operator.
Description: Convert to INTERVAL type.
X is of type INTEGER, REAL, or INTERVAL.
Y (optional) is of type INTEGER or REAL. If X is of type INTERVAL, Y must not be present.
KIND (optional) is a scalar INTEGER initialization expression.
Result characteristics: INTERVAL
If KIND is present, its value is used to determine the result's KTPV; otherwise, the result's KTPV is the same as a default interval.
Containment is guaranteed if X is an interval. For example, given
the result of INTERVAL(X, KIND=4) contains the INTERVAL X.
However, given REAL(8) X, Y, the result of INTERVAL(X,Y,KIND=4) does not necessarily contain the internal interval X .IH. Y. The reason is that X and Y can be REAL expressions, the values of which cannot be guaranteed.
The INTERVAL constructor does not necessarily contain the value of a literal INTERVAL constant with the same endpoints. For example, INTERVAL(1.1,1.3) does not necessarily contain the external value ev([1.1, 1.3]) = [1.1, 1.3]. The reason is that the internal values of REAL constants are approximations with unknown accuracy.
To construct an interval that always contains two REAL values, use the interval hull operator .IH., as shown in CODE EXAMPLE 2-18.
Result value: The interval result value is a valid interval.
If Y is absent and X is an interval, then INTERVAL(X [,KIND]) is an interval containing X and INTERVAL(X [,KIND]) is an interval with left and right endpoints [XL,XU], where
XL = REAL(INF(X) [,KIND]) rounded down, so that XL .LE. INF(X)
XU = REAL(SUP(X)[,KIND]) rounded up, so that XU.GE.SUP(X).
If both X and Y are present (and are therefore not intervals), then INTERVAL(X,Y [,KIND]) is an interval with left and right endpoints equal to REAL(X [,KIND]) and REAL(Y [,KIND]) respectively.
|
Note - In this case, rounding direction is not specified. Therefore, containment is not provided. |
[-inf,inf] is returned in two cases:
The intrinsic INTERVAL constructor function can be used in two ways:
Given the non-INTERVAL (REAL or INTEGER) expression, EXP, the code
The later will evaluate EXP as an interval expression. In the first two code fragments, the expression EXP is evaluated as a non-INTERVAL expression, and the result is used to construct a degenerate interval.
With two arguments, EXP1 and EXP2, INTERVAL(EXP1, EXP2) insulates both expressions from widest-need expression processing and constructs an interval with endpoints equal to the result of the non-INTERVAL evaluation of the expressions.
Including the KIND parameter makes it possible to control the KTPV of the result. This is most often needed under -strict expression processing where explicit KTPV conversions are necessary.
The intrinsic INTERVAL function with non-INTERVAL arguments should be used with care. Whenever interval containment is desired, use the interval hull operator .IH., as shown in CODE EXAMPLE 2-18.
The INTERVAL constructor acts as a boundary between INTERVAL and REAL or INTEGER expressions. On the non-INTERVAL side of this boundary, accuracy (and therefore containment) guarantees cannot be enforced.
See Section 2.9.2, INTERVAL (X [,Y, KIND]) for details on the use of the intrinsic INTERVAL constructor function.
As shown in TABLE 2-12, the intrinsic INTERVAL constructor function can be called using a KTPV-specific form that does not use the optional KIND parameter.
The three examples in this section illustrate how to use the intrinsic INTERVAL constructor to perform conversions from REAL to INTERVAL type data items. CODE EXAMPLE 2-19 shows that REAL expression arguments of the INTERVAL constructor are evaluated using REAL arithmetic and are, therefore, insulated from widest-need expression evaluations.
CODE EXAMPLE 2-19 notes:
CODE EXAMPLE 2-20 shows how the INTERVAL constructor can be used to construct the smallest possible interval, Y, such that the endpoints of Y are not elements of a given interval, X.
Given an interval X, a sharp interval Y satisfying the condition X .INT. Y is constructed. For information on the interior set relation, Section 2.8.3, Interior: (X .INT. Y).
CODE EXAMPLE 2-21 illustrates when the INTERVAL constructor returns the interval [-INF, INF] and [MAX_FLOAT, INF].
CODE EXAMPLE 2-21 notes:
The f95 specific names for intrinsic generic INTERVAL functions end with the generic name of the intrinsic and start with V, followed by S, D, or Q for arguments of type INTERVAL(4), INTERVAL(8), and INTERVAL(16), respectively.
In f95, only the following specific intrinsic functions are supported for the INTERVAL(16) data type: VQABS, VQAINT, VQANINT, VQINF, VQSUP, VQMID, VQMAG, VQMIG, and VQISEMPTY.
To avoid name space clashes in non-interval programs, the specific names are made available only by the command line options:
See Section 2.3.3, Interval Command-Line Options for more information.
All the supported intrinsic functions have specific names. For example, TABLE 2-13 lists the names for the INTERVAL version of the ABS intrinsic.
The remaining specific intrinsic functions are listed in Section 2.10.4.5, Intrinsic Functions.
This section describes the INTERVAL statements recognized by f95. The syntax and description of each statement is given, along with possible restrictions and examples.
An INTERVAL statement is used to declare INTERVAL named constants, variables, and function results. INTERVAL is an intrinsic numeric type declaration statement with the same syntax and semantics as standard numeric type declaration statements. The same specifications are available for use with the INTERVAL statement as exist for use in other numeric type declarations.
Description: The declaration can be INTERVAL, INTERVAL(4), INTERVAL(8), or INTERVAL(16).
the variable, W, has the default INTERVAL KTPV of 8 and occupies 16 bytes of contiguous memory. In Sun Studio Fortran 95, the default INTERVAL KTPV is not altered by the command-line options -xtypemap or -r8const.
INTERVAL cannot be used as a derived type name. For example the code in CODE EXAMPLE 2-22 is illegal.
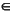 {4, 8, 16}
{4, 8, 16}the variable, W, has KTPV = n and occupies 2n bytes of contiguous memory.
CODE EXAMPLE 2-23 contains INTERVAL variable declarations with different KTPVs. Widest-need and strict value alignment is also shown.
CODE EXAMPLE 2-24 illustrates how to declare and initialize INTERVAL variables. See Section 2.1.2, INTERVAL Constants regarding the different ways to represent INTERVAL constants.
In any initializing declaration statement, if the type of the data expression does not match the type of the symbolic name, type conversion is performed.
math% cat ce2-25.f95 INTERVAL(4) :: R(5), S(5) INTERVAL :: U(5), V(5) INTERVAL(16) :: X(5), Y(5) END math% f95 -xia ce2-25.f95 math% a.out |
The syntax for DATA statements containing INTERVAL variables is the same as for other numeric data types except that INTERVAL variables are initialized using INTERVAL constants.
math% cat ce2-26.f95 INTERVAL X DATA X/[1,2]/ END math% f95 -xia ce2-26.f95 math% a.out |
Any INTERVAL variables or arrays may appear in an EQUIVALENCE statement with the following restriction: If an equivalence set contains an INTERVAL variable or array, all of the objects in the equivalence set must have the same type, as shown in CODE EXAMPLE 1-18. This is a standard, not interval-specific, Fortran restriction.
The repeatable edit descriptors for intervals are:
Fw.d, VFw.d, Dw.d, VDw.d, Dw.dEe, VDw.dEe, Yw.d, and Yw.dEe
w and e are nonzero, unsigned integer constants
d is an unsigned integer constant.
See Section 2.10.2, Input and Output for the specifications of how edit descriptors process INTERVAL data.
All standard Fortran edit descriptors accept intervals. The prefix V can be added to the standard E, F, and G edit descriptors for interval-only versions.
As shown in CODE EXAMPLE 2-27, no modifications to nonrepeatable edit descriptors are required when reading or writing INTERVAL data.
The repeatable edit descriptors E, F, EN, ES, G, VE, VEN, VES, VF, VG, and Y specify how INTERVAL data are edited.
CODE EXAMPLE 2-28 contains examples of INTERVAL-specific edit descriptors.
See Section 2.10.2, Input and Output for additional examples.
As shown in CODE EXAMPLE 2-29, there is no difference between an interval and a non-interval external function, except for the use of INTERVAL types (INTERVAL, INTERVAL(4), INTERVAL(8), or INTERVAL(16)) in the function's and argument's definitions.
The default INTERVAL in line 1 can be made explicit, as shown in CODE EXAMPLE 2-30.
Use the IMPLICIT attribute to specify the default type of interval names.
Use the INTRINSIC statement to declare intrinsic functions, so they can be passed as actual arguments.
INTRINSIC VDSIN, VDCOS, VSSIN, VSCOS X = CALC(VDSIN, VDCOS, VSSIN, VSCOS) |
|
Note - Specific names of generic functions must be used in the INTRINSIC statement and passed as actual arguments. See Section 2.9.3, Specific Names for Intrinsic Generic INTERVAL Functions and Section 2.10.4.5, Intrinsic Functions. |
Because they are generic, the following intrinsic INTERVAL functions cannot be passed as actual arguments:
The NAMELIST statement supports intervals.
CHARACTER(8) :: NAME CHARACTER(4) :: COLOR INTEGER :: AGE INTERVAL(4) :: HEIGHT INTERVAL(4) :: WEIGHT NAMELIST /DOG/ NAME, COLOR, AGE, WEIGHT, HEIGHT |
The PARAMETER attribute is used to assign the result of an INTERVAL initialization to a named constant (PARAMETER).
PARAMETER (p = e [, p = expr]...)
expr INTERVAL constant expression
= assigns the value of e to the symbolic name, p
Both the symbolic name, p, and the constant expression, expr, must have INTERVAL types.
Exponentiation to an integer power is allowed in constant expressions.
Mixed-mode INTERVAL expression evaluation is supported in the definition of interval named constants under widest-need expression processing. If the constant expression's type does not match the named constant's type, type conversion of the constant expression is performed under widest-need expression processing.
In standard Fortran 95, named constants cannot be used to represent the infimum and supremum of an INTERVAL constant. This is a known error that this constraint is not enforced in this release.
Intervals can be associated with pointers.
A statement function can be used to declare and evaluate parameterized INTERVAL expressions. Non-INTERVAL statement function restrictions apply.
math% cat ce2-35.f95 INTERVAL :: X, F F(X) = SIN(X)**2 + COS(X)**2 IF(1 .IN. F([0.5])) PRINT *, 'Check' END math% f95 -xia ce2-35.f95 math% a.out Check |
The type statement specifies the data type of variables in a variable list. Optionally the type statement specifies array dimensions, and initializes variables with values.
The syntax is the same as for non-INTERVAL numeric data types, except that type can be one of the following INTERVAL type specifiers: INTERVAL, INTERVAL(4), INTERVAL(8), or INTERVAL(16).
Properties of the type statement are the same for INTERVAL types as for other numeric data types.
Same as for non-INTERVAL numeric types.
math% cat ce2-36.f95 INTERVAL :: I,J = [0.0] INTERVAL(16) :: K = [0.1, 0.2_16] INTERVAL(16) :: L = [0.1] END math% f95 -xia ce2-36.f95 math% a.out |
CODE EXAMPLE 2-36 notes:
The WRITE statement accepts INTERVAL variables and processes an input/output list in the same way that non-INTERVAL type variables are processed. Formatted writing of INTERVAL data is performed using the defined INTERVAL edit descriptors. NAMELIST-directed WRITE statements support intervals.
The READ statement accepts INTERVAL variables and processes an input/output list in the same way that non-INTERVAL type variables are processed.
The process of performing INTERVAL input/output is the same as for other non-INTERVAL data types.
Let x be an external (decimal) number that can be read or written using either list-directed or formatted input/output. See the subsections in Section 2.1, Fortran Extensions regarding the regarding the distinction between internal approximations and external values. Such a number can be used to represent either an external interval, or an endpoint. There are three displayable forms of an external interval:
A positive or negative infinite interval endpoint is input/output as a case-insensitive string INF or INFINITY prefixed with a minus or an optional plus sign.
The empty interval is input/output as the case-insensitive string EMPTY enclosed in square brackets, "[...]". The string, EMPTY, may be preceded or followed by blanks.
CODE EXAMPLE 1-6 can be used to experiment with extended intervals.
See Section 2.4.1, Arithmetic Operators +, -, *, /, for more details.
On input, any external interval, X, or its components, X_inf and X_sup, can be formatted in any way that is accepted by the Dw.d edit descriptor. Therefore, let input-field, input-field1, and input-field2 be valid input fields for the Dw'.d, Dw1.d, and Dw2.d edit descriptors, respectively.
Let w be the width of an interval input field. On input, w must be greater than zero. All INTERVAL edit descriptors accept input INTERVAL data in each of the following three forms:
The first form (two numbers enclosed in brackets and separated by a comma) is the familiar [inf, sup] representation.
The second form (a single number enclosed in brackets) denotes a point or degenerate interval.
The third form (without brackets) is the single-number form of an interval in which the last displayed digit is used to determine the interval's width. See Section 2.10.2.7, Single-Number Editing With the Y Edit Descriptor. For more detailed information, see M. Schulte, V. Zelov, G.W. Walster, D. Chiriaev, "Single-Number Interval I/O," Developments in Reliable Computing, T. Csendes (ed.), (Kluwer 1999).
If an infimum is not internally representable, it is rounded down to an internal approximation known to be less than the exact value. If a supremum is not internally representable, it is rounded up to an internal approximations known to be greater than the exact input value. If the degenerate interval is not internally representable, it is rounded down and rounded up to form an internal INTERVAL approximation known to contain the exact input value.
If an input list item is an INTERVAL, the corresponding element in the input record must be an external interval or a null value.
An external interval value may have the same form as an INTERVAL, REAL, or INTEGER literal constant. If an interval value has the form of a REAL or INTEGER literal constant with no enclosing square brackets, "["... "]", the external interval is interpreted using the single-number interval representation: [x] + [-1,1]uld (unit in the last digit).
When using the [inf, sup] input style, an end of record may occur between the infimum and the comma or between the comma and the supremum.
A null value, specified by two consecutive commas, means that the corresponding INTERVAL list item is unchanged.
|
Note - Do not use a null value for the infimum or supremum of an interval. |
The INTERVAL edit descriptors are:
In the INTERVAL edit descriptors:
The parameters w and d must be used. Ee is optional
The w and d specifiers must be present and are subject to the following constraints:
Input actions for formatted interval input are the same as for other numeric data types, except that in all cases, the stored internal approximation contains the external value represented by the input character string. Containment can require outward rounding of interval endpoints. Given any input interval characters, input_string, the corresponding external value, ev(input_string), and the resulting internal approximation after input conversion, X, are related:
During input, all interval edit descriptors have the same semantics. The value of parameter w, is the field width containing the external interval. The value of e is ignored.
Output actions for formatted interval output are the same as for other data types, except that in all cases, the mathematical value of the output character string must contain the mathematical value of the internal data item in the output list. Containment can require outward rounding of interval endpoints. Given any internal interval, X, the corresponding output characters, output_string, and the external value, ev(output_string), are related:
During output, edit descriptors cause the internal value of interval output list items to be displayed using different formats. However, the containment constraint requires that
ev(input_string) 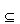 X
X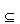 ev(output_string)
ev(output_string)
The behavior of formatted input is identical for all INTERVAL edit descriptors listed in Section 2.10.2.4, Formatted Input/Output. All inputs described in Section 2.10.2.2, Input are accepted.
If the input field contains a decimal point, the value of d is ignored. If a decimal point is omitted from the input field, d determines the position of the decimal point in the input value; that is, the input value is read as an integer and multiplied by 10(-d).
Because trailing zeros are significant in single-number INTERVAL input, the BZ control edit descriptor is ignored when processing leading and trailing blanks for input to INTERVAL list items.
The P edit descriptor changes the scale factor for Y, VE, VEN, VES, VF, and VG descriptors and for F, E, EN, ES, and G edit descriptors when applied to intervals. The P edit descriptor scales interval endpoints the same way it scales REAL values.
The F, E, EN, ES, and G edit descriptors applied to intervals have the same meaning as the Y edit descriptor except that if the F or G edit descriptor is used, the output field may be formatted using the F edit descriptor. If the E edit descriptors are used, the output field always has the form prescribed by the corresponding E, EN, or ES edit descriptor.
Formatted INTERVAL output has the following properties:
On output, the default values for the exponent field, e, are shown in TABLE 2-14.
The Y edit descriptor formats extended interval values in the single-number form.
If the external INTERVAL value is not degenerate, the output format is the same as for a REAL or INTEGER literal constant (X without square brackets, "["..."]"). The external value is interpreted as a non-degenerate mathematical interval [x] + [-1,1]uld. The general form of the Y edit descriptor is:
The d specifier sets the number of places allocated for displaying significant digits. However, the actual number of displayed digits may be more or less than d, depending on the value of w and the width of the external interval.
The e specifier (if present) defines the number of places in the output subfield reserved for the exponent.
The presence of the e specifier forces the output field to have the form prescribed by the E (as opposed to F) edit descriptor.
The single-number interval representation is often less precise than the [inf, sup] representation. This is particularly true when an interval or its single-number representation contains zero or infinity.
For example, the external value of the single-number representation for [-15, +75] is ev([0E2]) = [-100, +100]. The external value of the single-number representation for [1, 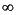 ] is ev([0E+inf]) =
] is ev([0E+inf]) = ![[-inf, +inf] [-inf, +inf]](figures/iapgFreference-93.gif) .
.
In these cases, to produce a narrower external representation of the internal approximation, the VGw.d'Ee edit descriptor is used, with d' 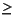 1 to display the maximum possible number of significant digits within the w-character input field.
1 to display the maximum possible number of significant digits within the w-character input field.
If it is possible to represent a degenerate interval within the w-character output field, the output string for a single number is enclosed in obligatory square brackets, "[", "]" to signify that the result is a point.
If there is sufficient field width, the E or F edit descriptor is used, depending on which can display the greater number of significant digits. If the number of displayed digits using the E and F edit descriptor is the same, the F edit descriptor is used.
Increasing interval width decreases the number of digits displayed in the single-number representation. When the interval is degenerate all remaining positions are filled with zeros and brackets are added if the degenerate interval value is represented exactly.
The intrinsic function NDIGITS (see TABLE 2-22) returns the maximum number of significant digits necessary to write an INTERVAL variable or array using the single-number display format.
For readability, the decimal point is always located in position p = e + d + 4, counting from the right of the output field.
The optional e specifier specifies the number of exponent digits. If the number of exponent digits is specified, w must be at least d + e + 7.
The E, EN, and ES edit descriptors format INTERVAL data items using the single-number E, EN, and ES forms of the Y edit descriptor.
The F edit descriptor formats INTERVAL data items using only the F form of the INTERVAL Y edit descriptor. The general form is:
Using the F descriptor, it is possible to display more significant digits than specified by d. Positions corresponding to the digits that are not displayed are filled with blanks.
The G edit descriptor formats INTERVAL data items using the single-number E or F form of the Y edit descriptor. The general form is:
|
Note - If it is impossible to output interval endpoints according to the F descriptor, G edit descriptor uses the E descriptor |
The general form of the VE edit descriptor is:
Let Xd be a valid external value using the Ew'.d edit descriptor. The VE edit descriptor outputs INTERVAL data items in the following form:
[X_inf,X_sup], where w' = (w-3)/2 .
The external values, X_inf and X_sup, are lower and upper bounds, respectively, on the infimum and supremum of the INTERVAL output list item.
The general form of the VEN edit descriptor is:
Let X_inf and X_sup be valid external values displayed using the ENw'.d edit descriptor. The VEN edit descriptor outputs an INTERVAL data item in the following form:
[X_inf,X_sup], where w' = (w-3)/2 .
The external values, X_inf and X_sup, are lower and upper bounds, respectively, on the infimum and supremum of the INTERVAL output list item.
The general form of the VES edit descriptor is:
Let X_inf and X_sup be a valid external values using the ESw'.d edit descriptor. The VES edit descriptor outputs an INTERVAL data item in the following form:
[X_inf,X_sup], where w' = (w-3)/2 .
The external values, X_inf and X_sup, are lower and upper bounds, respectively, on the infimum and supremum of the INTERVAL output list item.
Let X_inf and X_sup be valid external values displayed using the Fw'.d edit descriptor. The VF edit descriptor outputs INTERVAL data items in the following form:
[X_inf,X_sup], where w' = (w-3)/2 .
The external values, X_inf and X_sup, are lower and upper bounds, respectively, on the infimum and supremum of the INTERVAL output list item.
|
Note - If it is impossible to output an interval endpoint according to the specified interval edit descriptor, asterisks are printed. For example, [0.9999, ******] |
For INTERVAL output, VG editing is the same as VE or VF editing, except that the G edit descriptor is used to format the displayed interval endpoints.
|
Note - If it is impossible to output interval endpoints according to the F descriptor, the VG edit descriptor uses the E descriptor. |
Unformatted input/output is used to transfer data to and from memory locations without changing its internal representation. With intervals, unformatted input/output is particularly important, because outward rounding on input and output is avoided.
REAL constants for left and right endpoints are produced using either an F or an E edit descriptor. Let |x| be the absolute value of an output interval endpoint. Then if
the endpoint is produced using the 0PFw.d edit descriptor. Otherwise, the 1PEw.dEe descriptor is used. In f95, d1 = -2 and d2 = +8.
For the output of INTERVAL data items in f95, the values for d and e are the same as for the REAL types with the same KTPV. The value of w reflects the need to conveniently accommodate two REAL values and three additional characters for square brackets, "[", "]", and the comma, as shown in CODE EXAMPLE 2-37.
Single-number INTERVAL input, immediately followed by output, can appear to suggest that a decimal digit of accuracy has been lost, when in fact radix conversion has caused a 1 or 2 ulp increase in the width of the stored input interval. For example, an input of 1.37 followed by an immediate print will result in 1.3 being output. See Section 2.10.2.4, Formatted Input/Output.
As shown in CODE EXAMPLE 1-6, programs must use character input and output to exactly echo input values and internal reads to convert input character strings into valid internal approximations.
This section contains the defining properties of the f95 intrinsic INTERVAL functions.
Generic intrinsic INTERVAL functions that accept arguments with more than one KTPV have both generic and KTPV-specific names. When an intrinsic function is invoked using its KTPV-specific name, arguments must have the matching KTPV.
|
Note - In f95, some KTPV-16 specific intrinsic functions are not provided. This is an outstanding quality of implementation opportunity. |
With functions that accept more than one INTERVAL data item (for example, SIGN(A,B)), all arguments must have the same KTPV. Under widest-need expression processing, compliance with this restriction is automatic. With strict expression processing, developers are responsible for enforcing type and KTPV restrictions on intrinsic function arguments. Compile-time errors result when different KTPVs are encountered.
This section lists the type-conversion, trigonometric, and other functions that accept INTERVALarguments. The symbols ![x underlinex bar[inf(x), sup(x)] x underlinex bar[inf(x), sup(x)]](figures/iapgFreference-95.gif) and
and ![x underlinex bar[inf(x), sup(x)] x underlinex bar[inf(x), sup(x)]](figures/iapgFreference-96.gif) in the interval
in the interval ![x underlinex bar[inf(x), sup(x)] x underlinex bar[inf(x), sup(x)]](figures/iapgFreference-97.gif) are used to denote its ordered elements, the infimum, or lower bound and supremum, or upper bound, respectively. In point (non-interval) function definitions, lowercase letters xand yare used to denote REALor INTEGERvalues.
are used to denote its ordered elements, the infimum, or lower bound and supremum, or upper bound, respectively. In point (non-interval) function definitions, lowercase letters xand yare used to denote REALor INTEGERvalues.
When evaluating a function, f, of an interval argument, X, the interval result, f(X), must be an enclosure of its containment set, f(x). Therefore,
A similar result holds for functions of n-variables. Determining the containment set of values that must be included when the interval ![[inf(x), sup(x)] [inf(x), sup(x)]](figures/iapgFreference-99.gif) contains values outside the domain of fis discussed in the supplementary paper [1] cited in Section 2.11, References. The results therein are needed to determine the set of values that a function can produce when evaluated on the boundary of, or outside its domain of definition. This set of values, called the containment set is the key to defining interval systems that return valid results, no matter what the value of a function's arguments or an operator's operands. As a consequence, there are no argument restrictions on any intrinsic INTERVALfunctions in f95.
contains values outside the domain of fis discussed in the supplementary paper [1] cited in Section 2.11, References. The results therein are needed to determine the set of values that a function can produce when evaluated on the boundary of, or outside its domain of definition. This set of values, called the containment set is the key to defining interval systems that return valid results, no matter what the value of a function's arguments or an operator's operands. As a consequence, there are no argument restrictions on any intrinsic INTERVALfunctions in f95.
The function DIVIX returns the interval enclosure of the result of the interval division operation (A/B) intersected with the interval C.
In the case when A contains zero, the mathematical result of the interval division operation (A/B) is the union of two disjoint intervals. Each interval in the union can be represented in the currently implemented interval arithmetic system. The DIVIX function is a convenient way to compute one or both of these intervals.
This sections provides additional information about the inverse tangent function. For further details, see the supplementary paper [9] cited in Section 2.11, References.
Description: Interval enclosure of the inverse tangent function over a pair of intervals.
Special values: TABLE 2-15 and CODE EXAMPLE 2-54 display the ATAN2 indeterminate forms.
|
|
|
|
||
|---|---|---|---|---|
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
Arguments: Y is of type INTERVAL. X is of the same type and KIND type parameter as Y.
Result characteristics: Same as the arguments.
Result value: The interval result value is an enclosure for the specified interval. An ideal enclosure is an interval of minimum width that contains the exact mathematical interval in the description.
The result is empty if one or both arguments are empty.
In the case where x< 0 and 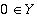 , to get a sharp interval enclosure (denoted by
, to get a sharp interval enclosure (denoted by 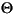 ), the following convention uniquely defines the set of all possible returned interval angles:
), the following convention uniquely defines the set of all possible returned interval angles:
This convention, together with
results in a unique definition of the interval angles 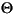 that ATAN2(Y, X) must include.
that ATAN2(Y, X) must include.
TABLE 2-16 contains the tests and arguments of the REAL ATAN2 function that are used to compute the endpoints of 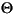 in the algorithm that satisfies the constraints required to produce sharp interval angles. The first two columns define the distinguishing cases. The third column contains the range of possible values of the midpoint, m(
in the algorithm that satisfies the constraints required to produce sharp interval angles. The first two columns define the distinguishing cases. The third column contains the range of possible values of the midpoint, m(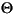 ), of the interval
), of the interval 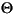 . The last two columns show how the endpoints of
. The last two columns show how the endpoints of 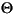 are computed using the REAL ATAN2 intrinsic function. Directed rounding must be used to guarantee containment.
are computed using the REAL ATAN2 intrinsic function. Directed rounding must be used to guarantee containment.
|
|
|
|
||
|
|
|
|||
|
|
|
|
Description: Range of maximum.
The containment set for max(X1,..., Xn) is:
The implementation of the MAX intrinsic must satisfy:
MAX(X1,X2,[X3, ...])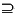 {max(X1, ..., Xn)}.
{max(X1, ..., Xn)}.
Arguments: The arguments are of type INTERVAL and have the same type and KIND type parameter.
Result characteristics: The result is of type INTERVAL. The kind type parameter is that of the arguments.
Description: Range of minimum.
The containment set for min(X1,..., Xn) is:
The implementation of the MIN intrinsic must satisfy:
MIN(X1,X2,[X3, ...]) {min(X1, ..., Xn)}.
{min(X1, ..., Xn)}.
Arguments: The arguments are of type INTERVAL and have the same type and KIND type parameter.
Result characteristics: The result is of type INTERVAL. The kind type parameter is that of the arguments.
Tables TABLE 2-19 through TABLE 2-22 list the properties of intrinsic functions that accept interval arguments. TABLE 2-17 lists the tabulated properties of intrinsic INTERVAL functions in these tables.
KTPV 4, 8 and 16 versions of intrinsic INTERVAL functions are defined. The corresponding specific intrinsic names begin with VS, VD or VQ, from interVal Single, Double and Quad.
For each specific REAL intrinsic function, a corresponding intrinsic INTERVAL function exists with a VS, VD, or VQ prefix, such as VSSIN() and VDSIN().
Because indeterminate forms are possible, special values of the X**Y and ATAN2 function are contained in Section 2.5, Power Operators X**N and X**Y and Section 2.10.4.2, Inverse Tangent Function ATAN2(Y,X), respectively. The remaining intrinsic functions do not require this treatment.
(1) arctan(a/b) = 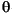 , given a = h sin , given a = h sin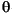 , b = h cos , b = h cos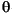 , and h2 = a2 + b2. , and h2 = a2 + b2.
|
||||||
|---|---|---|---|---|---|---|
RANDOM_NUMBER(HARVEST) returns through the interval variable HARVEST one pseudorandom interval [a, b], or an array of pseudorandom intervals from uniform distributions over the ranges 0 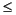 a
a 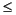 1, and a
1, and a 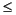 b
b 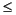 1.
1.
The following technical reports are available online. See the Interval Arithmetic Readme for the location of these files.
1. G.W. Walster, E.R. Hansen, and J.D. Pryce, "Extended Real Intervals and the Topological Closure of Extended Real Relations," Technical Report, Sun Microsystems. February 2000.
2. G. William Walster, "Empty Intervals," Technical Report, Sun Microsystems. April 1998.
3. G. William Walster, "Closed Interval Systems," Technical Report, Sun Microsystems. August 1999.
4. G. William Walster, "Literal Interval Constants," Technical Report, Sun Microsystems. August 1999.
5. G. William Walster, "Widest-Need Interval Expression Evaluation," Technical Report, Sun Microsystems. August 1999.
6. G. William Walster, "Compiler Support of Interval Arithmetic With Inline Code Generation and Nonstop Exception Handling," Technical Report, Sun Microsystems. February 2000.
7. G. William Walster, "Finding Roots on the Edge of a Function's Domain," Technical Report, Sun Microsystems. February 2000.
8. G. William Walster, "Implementing the `Simple' Closed Interval System," Technical Report, Sun Microsystems. February 2000.
9. G. William Walster, "Interval Angles and the Fortran ATAN2 Intrinsic Function," Technical Report, Sun Microsystems. February 2000.
10. G. William Walster, "The `Simple' Closed Interval System," Technical Report, Sun Microsystems. February 2000.
11. G. William Walster, Margaret S. Bierman, "Interval Arithmetic in Forte Developer Fortran," Technical Report, Sun Microsystems. March 2000.
Copyright © 2005, Sun Microsystems, Inc. All Rights Reserved.