Scenario: Parallelizing Loops with LoopTool
IMSL(TM) is a popular math library used by many FORTRAN and C programmers. [IMSL is a registered trademark of IMSL, Inc. This example is used with permission.] One of its routines is a good candidate for parallelizing with LoopTool.
This example is a FORTRAN program called l2trg.f(). (It computes LU factorization of a single-precision general matrix.) The program is compiled without any parallelization, then checked to see how long it takes to run with the time(1) command.
Example 8-3 Original Times for l2trg.f() (Not Parallelized)
$ f77 l2trg.f -cg92 -03 -lmsl $ /bin/time a.out real 44.8 user 43.5 sys 1.0
To look at the program with LoopTool, recompile with the LoopTool instrumentation, using the -Zlp option.
$ f77 l2trg.f -cg92 -03 -Zlp -lmsl
Start LoopTool. Figure 8-8shows the initial Overview screen.
Figure 8-8 LoopTool View Before Parallelization
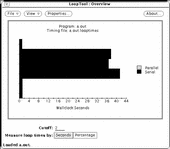
Most of the program's time is spent in three loops; each loop indicated by a horizontal bar.
The LoopTool user interface brings up various screens triggerred by cursor movement and mouse actions. In the Overview window:
Put the cursor over a loop to get its line number.
Click on the loop to bring up a window that displays the loop's source code.
In our example, we clicked on the middle horizontal bar to look at the source code for the middle loop. The source code reveals that loops are nested.
Figure 8-9 shows the Source and Hints window for the middle loop.
Figure 8-9 LoopTool (Source and Hints Window)
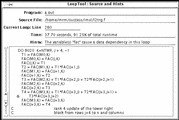
In this case, LoopTool gives the Hints message:
The variable "fac" causes a data dependency in this loop
In the source code, you can see that fac is calculated in the nested, innermost loop (9030):
C update the remaining rectangular
C block of U, rows j to j+3 and
C columns j+4 to n
DO 9020 K=NTMP, J + 4, -1
T1 = FAC(M0,K)
FAC(M0,K) = FAC(J,K)
FAC(J,K) = T1
T2 = FAC(M1,K) + T1*FAC(J+1,J)
FAC(M1,K) = FAC(J+1,K)
FAC(J+1,K) = T2
T3 = FAC(M2,K) + T1*FAC(J+2,J) + T2*FAC(J+2,J+1)
FAC(M2,K) = FAC(J+2,K)
FAC(J+2,K) = T3
T4 = FAC(M3,K) + T1*FAC(J+3,J) + T2*FAC(J+3,J+1) +
& T3*FAC(J+3,J+2)
FAC(M3,K) = FAC(J+3,K)
FAC(J+3,K) = T4
C rank 4 update of the lower right
C block from rows j+4 to n and columns
C j+4 to n
DO 9030 I=KBEG, NTMP
FAC(I,K) = FAC(I,K) + T1*FAC(I,J) + T2*FAC(I,J+1) +
& T3*FAC(I,J+2) + T4*FAC(I,J+3)
9030 CONTINUE
9020 CONTINUE
The loop index, I, of the innermost loop is used to access rows of the array fac. So the innermost loop updates the Ith row of fac. Since updating these rows does not depend on updates of any other rows of fac, it's safe to parallelize this loop.
The calculation of fac is speeded up by parallelizing loop 9030, so there should be a significant performance improvement. Force explicit parallelization by inserting a DOALL directive in front of loop 9030:
C$PAR DOALL
(Add DOALL directive here)
DO 9030 I=KBEG, NTMP
FAC(I,K) = FAC(I,K) + T1*FAC(I,J) + T2*FAC(I,J+1) +
& T3*FAC(I,J+2) + T4*FAC(I,J+3)
9030 CONTINUE
Now you can recompile the FORTRAN code, run the program, and compare the new time with the original times. More specifically, Example 8-4 shows the use of all the processors on the machine by setting the PARALLEL environment variable equal to 2, and forces explicit parallelization of that loop with the -explicitpar compiler option.
Finally, run the program and compare its time with that of the original times (shown in Example 8-3).
Example 8-4 Post-Parallelization Times for l2trg.f()
$ setenv PARALLEL 2 (2 is the # of processors on the machine) $ f77 l2trg.f -cg92 -03 -explicitpar -imsl $ /bin/time a.out real 28.4 user 53.8 sys 1.1
The program now runs over a third faster. (The higher number for user reflects the fact that there are now two processes running.) Figure 8-10 shows the LoopTool Overview window. You see that, in fact, the innermost loop is now parallel.
Figure 8-10 LoopTool View After Parallelization
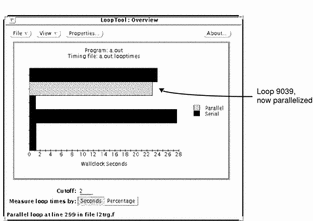
- © 2010, Oracle Corporation and/or its affiliates
