Release 2 (9.2)
Part Number A96520-01
Home |
Book List |
Contents |
Index |
 Master Index |
 Feedback |
| Oracle9i Data Warehousing Guide Release 2 (9.2) Part Number A96520-01 |
|
This chapter discusses how Oracle rewrites queries. It contains:
One of the major benefits of creating and maintaining materialized views is the ability to take advantage of query rewrite, which transforms a SQL statement expressed in terms of tables or views into a statement accessing one or more materialized views that are defined on the detail tables. The transformation is transparent to the end user or application, requiring no intervention and no reference to the materialized view in the SQL statement. Because query rewrite is transparent, materialized views can be added or dropped just like indexes without invalidating the SQL in the application code.
Before the query is rewritten, it is subjected to several checks to determine whether it is a candidate for query rewrite. If the query fails any of the checks, then the query is applied to the detail tables rather than the materialized view. This can be costly in terms of response time and processing power.
The Oracle optimizer uses two different methods to recognize when to rewrite a query in terms of one or more materialized views. The first method is based on matching the SQL text of the query with the SQL text of the materialized view definition. If the first method fails, the optimizer uses the more general method in which it compares joins, selections, data columns, grouping columns, and aggregate functions between the query and a materialized view.
Query rewrite operates on queries and subqueries in the following types of SQL statements:
It also operates on subqueries in the set operators UNION, UNION ALL, INTERSECT, and MINUS, and subqueries in DML statements such as INSERT, DELETE, and UPDATE.
Several factors affect whether or not a given query is rewritten to use one or more materialized views:
There is also an explain rewrite procedure which will advise whether query rewrite is possible on a query and if so, which materialized views will be used.
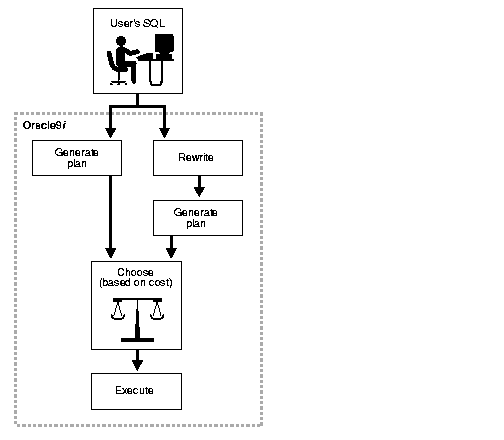
Query rewrite is available with cost-based optimization. Oracle optimizes the input query with and without rewrite and selects the least costly alternative. The optimizer rewrites a query by rewriting one or more query blocks, one at a time.
If the rewrite logic has a choice between multiple materialized views to rewrite a query block, it will select the one which can result in reading in the least amount of data.
After a materialized view has been picked for a rewrite, the optimizer performs the
rewrite, and then tests whether the rewritten query can be rewritten further with another materialized view. This process continues until no further rewrites are possible. Then the rewritten query is optimized and the original query is optimized. The optimizer compares these two optimizations and selects the least costly alternative.
Since optimization is based on cost, it is important to collect statistics both on tables involved in the query and on the tables representing materialized views. Statistics are fundamental measures, such as the number of rows in a table, that are used to calculate the cost of a rewritten query. They are created by using the DBMS_STATS package.
Queries that contain in-line or named views are also candidates for query rewrite. When a query contains a named view, the view name is used to do the matching between a materialized view and the query. When a query contains an inline view, the inline view can be merged into the query before matching between a materialized view and the query occurs.
In addition, if the inline view's text definition exactly matches with that of an inline view present in any eligible materialized view, general rewrite may be possible. This is because, whenever a materialized view contains exactly identical inline view text to the one present in a query, query rewrite treats such an inline view like a named view or a table.
Figure 22-1 presents a graphical view of the cost-based approach used during the rewrite process.
A query is rewritten only when a certain number of conditions are met:
enforced, then the materialized view will not be used.To determine this, the optimizer may depend on some of the data relationships declared by the user using constraints and dimensions. Such data relationships include hierarchies, referential integrity, and uniqueness of key data, and so on.
The following sections use an example schema and a few materialized views to illustrate how the optimizer uses data relationships to rewrite queries. Oracle's sh sample schema consists of these tables:
COSTS, COUNTRIES, CUSTOMERS, PRODUCTS, PROMOTIONS, TIMES, CHANNELS, SALES
| See Also:
Oracle9i Sample Schemas for details regarding the |
The query rewrite examples in this chapter mainly refer to the following materialized views. Note that those materialized views do not necessarily represent the most efficient implementation for the sh sample schema. Instead, they are a base for demonstrating Oracle's rewrite capabilities. Further examples demonstrating specific functionality can be found in the specific context.
The following materialized views contain joins and aggregates:
CREATE MATERIALIZED VIEW sum_sales_pscat_week_mv ENABLE QUERY REWRITE AS SELECT p.prod_subcategory, t.week_ending_day, SUM(s.amount_sold) AS sum_amount_sold FROM sales s, products p, times t WHERE s.time_id=t.time_id AND s.prod_id=p.prod_id GROUP BY p.prod_subcategory, t.week_ending_day; CREATE MATERIALIZED VIEW sum_sales_prod_week_mv ENABLE QUERY REWRITE AS SELECT p.prod_id, t.week_ending_day, s.cust_id, SUM(s.amount_sold) AS sum_amount_sold FROM sales s, products p, times t WHERE s.time_id=t.time_id AND s.prod_id=p.prod_id GROUP BY p.prod_id, t.week_ending_day, s.cust_id; CREATE MATERIALIZED VIEW sum_sales_pscat_month_city_mv ENABLE QUERY REWRITE AS SELECT p.prod_subcategory, t.calendar_month_desc, c.cust_city, SUM(s.amount_sold) AS sum_amount_sold, COUNT(s.amount_sold) AS count_amount_sold FROM sales s, products p, times t, customers c WHERE s.time_id=t.time_id AND s.prod_id=p.prod_id AND s.cust_id=c.cust_id GROUP BY p.prod_subcategory, t.calendar_month_desc, c.cust_city;
The following materialized views contain joins only:
CREATE MATERIALIZED VIEW join_sales_time_product_mv ENABLE QUERY REWRITE AS SELECT p.prod_id, p.prod_name, t.time_id, t.week_ending_day, s.channel_id, s.promo_id, s.cust_id, s.amount_sold FROM sales s, products p, times t WHERE s.time_id=t.time_id AND s.prod_id = p.prod_id; CREATE MATERIALIZED VIEW join_sales_time_product_oj_mv ENABLE QUERY REWRITE AS SELECT p.prod_id, p.prod_name, t.time_id, t.week_ending_day, s.channel_id, s.promo_id, s.cust_id, s.amount_sold FROM sales s, products p, times t WHERE s.time_id=t.time_id AND s.prod_id=p.prod_id(+);
You must collect statistics on the materialized views so that the optimizer can determine whether to rewrite the queries. You can do this either on a per object base or for all newly created objects without statistics.
On a per object base, shown for join_sales_time_product_mv:
EXECUTE DBMS_STATS.GATHER_TABLE_STATS ('SH','JOIN_SALES_TIME_PRODUCT_MV', estimate_percent=>20,block_sample=>TRUE,cascade=>TRUE);
For all newly created objects without statistics, on schema level:
EXECUTE DBMS_STATS.GATHER_SCHEMA_STATS('SH', options => 'GATHER EMPTY', estimate_percent=>20, block_sample=>TRUE, cascade=>TRUE);
| See Also:
Oracle9i Supplied PL/SQL Packages and Types Reference for further information about using the |
Several steps must be followed to enable query rewrite:
ENABLE QUERY REWRITE clause.QUERY_REWRITE_ENABLED must be set to true.OPTIMIZER_MODE to all_rows or first_rows, or by analyzing the tables and setting OPTIMIZER_MODE to choose.OPTIMIZER_FEATURES_ENABLE should be left unset for query rewrite to be possible. However, if it is given a value, then it must be set to at least 8.1.6 or query rewrite and explain rewrite will not be possible.If step 1 has not been completed, a materialized view will never be eligible for query rewrite. ENABLE QUERY REWRITE can be specified either when the materialized view is created, as illustrated here, or with the ALTER MATERIALIZED VIEW statement.
CREATE MATERIALIZED VIEW join_sales_time_product_mv ENABLE QUERY REWRITE AS SELECT p.prod_id, p.prod_name, t.time_id, t.week_ending_day, s.channel_id, s.promo_id, s.cust_id, s.amount_sold FROM sales s, products p, times t WHERE s.time_id=t.time_id AND s.prod_id = p.prod_id;
You can use the initialization parameter QUERY_REWRITE_ENABLED to disable query rewrite for all materialized views, or to enable it again for all materialized views that are individually enabled. However, the QUERY_REWRITE_ENABLED parameter cannot enable query rewrite for materialized views that have disabled it with the CREATE or ALTER statement.
The NOREWRITE hint disables query rewrite in a SQL statement, overriding the QUERY_REWRITE_ENABLED parameter, and the REWRITE hint (when used with mv_name) restricts the eligible materialized views to those named in the hint.
Query rewrite requires the following initialization parameter settings:
OPTIMIZER_MODE = all_rows, first_rows, or chooseQUERY_REWRITE_ENABLED = trueCOMPATIBLE = 8.1.0 (or greater)The QUERY_REWRITE_INTEGRITY parameter is optional, but must be set to stale_tolerated, trusted, or enforced if it is specified (see "Accuracy of Query Rewrite"). It defaults to enforced if it is undefined.
Because the integrity level is set by default to enforced, all constraints must be validated. Therefore, if you use ENABLE NOVALIDATE, certain types of query rewrite might not work. To enable query rewrite in this environment, you should set your integrity level to a lower level of granularity such as trusted or stale_tolerated.
| See Also:
"View Constraints" for details regarding view constraints and query rewrite |
With OPTIMIZER_MODE set to choose, a query will not be rewritten unless at least one table referenced by it has been analyzed. This is because the rule-based optimizer is used when OPTIMIZER_MODE is set to choose and none of the tables referenced in a query have been analyzed.
A materialized view is only eligible for query rewrite if the ENABLE QUERY REWRITE clause has been specified, either initially when the materialized view was first created or subsequently with an ALTER MATERIALIZED VIEW statement.
The initialization parameters described previously can be set using the ALTER SYSTEM SET statement. For a given user's session, ALTER SESSION can be used to disable or enable query rewrite for that session only. For example:
ALTER SESSION SET QUERY_REWRITE_ENABLED = TRUE;
You can set the level of query rewrite for a session, thus allowing different users to work at different integrity levels. The possible statements are:
ALTER SESSION SET QUERY_REWRITE_INTEGRITY = stale_tolerated; ALTER SESSION SET QUERY_REWRITE_INTEGRITY = trusted; ALTER SESSION SET QUERY_REWRITE_INTEGRITY = enforced;
Hints can be included in SQL statements to control whether query rewrite occurs. Using the NOREWRITE hint in a query prevents the optimizer from rewriting it.
The REWRITE hint with no argument in a query forces the optimizer to use a materialized view (if any) to rewrite it regardless of the cost.
The REWRITE(mv1,mv2,...) hint with arguments forces rewrite to select the most suitable materialized view from the list of names specified.
To prevent a rewrite, you can use the following statement:
SELECT /*+ NOREWRITE */ p.prod_subcategory, SUM(s.amount_sold) FROM sales s, products p WHERE s.prod_id=p.prod_id GROUP BY p.prod_subcategory;
To force a rewrite using sum_sales_pscat_week_mv, you can use the following statement:
SELECT /*+ REWRITE (sum_sales_pscat_week_mv) */ p.prod_subcategory, SUM(s.amount_sold) FROM sales s, products p WHERE s.prod_id=p.prod_id GROUP BY p.prod_subcategory;
Note that the scope of a rewrite hint is a query block. If a SQL statement consists of several query blocks (SELECT clauses), you might need to specify a rewrite hint on each query block to control the rewrite for the entire statement.
Use of a materialized view based not on privileges the user has on that materialized view, but on privileges the user has on detail tables or views in the query.
The system privilege GRANT QUERY REWRITE lets you enable materialized views in your own schema for query rewrite only if all tables directly referenced by the materialized view are in that schema. The GRANT GLOBAL QUERY REWRITE privilege allows you to enable materialized views for query rewrite even if the materialized view references objects in other schemas.
The privileges for using materialized views for query rewrite are similar to those for definer-rights procedures.
| See Also:
PL/SQL User's Guide and Reference for further information |
Query rewrite offers three levels of rewrite integrity that are controlled by the initialization parameter QUERY_REWRITE_INTEGRITY, which can either be set in your parameter file or controlled using an ALTER SYSTEM or ALTER SESSION statement. The three values it can take are:
enforced
This is the default mode. The optimizer will only use materialized views that it knows contain fresh data and only use those relationships that are based on ENABLED VALIDATED primary/unique/foreign key constraints.
trusted
In trusted mode, the optimizer trusts that the data in the materialized views is fresh and the relationships declared in dimensions and RELY constraints are correct. In this mode, the optimizer will also use prebuilt materialized views or materialized views based on views, and it will use relationships that are not enforced as well as those that are enforced. In this mode, the optimizer also 'trusts' declared but not ENABLED VALIDATED primary/unique key constraints and data relationships specified using dimensions.
stale_tolerated
In stale_tolerated mode, the optimizer uses materialized views that are valid but contain stale data as well as those that contain fresh data. This mode offers the maximum rewrite capability but creates the risk of generating inaccurate results.
If rewrite integrity is set to the safest level, enforced, the optimizer uses only enforced primary key constraints and referential integrity constraints to ensure that the results of the query are the same as the results when accessing the detail tables directly. If the rewrite integrity is set to levels other than enforced, there are several situations where the output with rewrite can be different from that without it.
DROP and MOVE PARTITION on the detail table could affect the results of the materialized view.The optimizer uses a number of different methods to rewrite a query. The first, most important step is to determine if all or part of the results requested by the query can be obtained from the precomputed results stored in a materialized view.
The simplest case occurs when the result stored in a materialized view exactly matches what is requested by a query. The Oracle optimizer makes this type of determination by comparing the text of the query with the text of the materialized view definition. This method is most straightforward but the number of queries eligible for this type of query rewrite will be minimal.
When the text comparison test fails, the Oracle optimizer performs a series of generalized checks based on the joins, selections, grouping, aggregates, and column data fetched. This is accomplished by individually comparing various clauses (SELECT, FROM, WHERE, HAVING, or GROUP BY) of a query with those of a materialized view.
The optimizer uses two methods:
In full text match, the entire text of a query is compared against the entire text of a materialized view definition (that is, the entire SELECT expression), ignoring the white space during text comparison. Given the following query:
SELECT p.prod_subcategory, t.calendar_month_desc, c.cust_city, SUM(s.amount_sold) AS sum_amount_sold, COUNT(s.amount_sold) AS count_amount_sold FROM sales s, products p, times t, customers c WHERE s.time_id=t.time_id AND s.prod_id=p.prod_id AND s.cust_id=c.cust_id GROUP BY p.prod_subcategory, t.calendar_month_desc, c.cust_city;
This query matches sum_sales_pscat_month_city_mv (white space excluded) and is rewritten as:
SELECT prod_subcategory, calendar_month_desc, cust_city, sum_amount_sold, count_amount_sold FROM sum_sales_pscat_month_city_mv;
When full text match fails, the optimizer then attempts a partial text match. In this method, the text starting from the FROM clause of a query is compared against the text starting with the FROM clause of a materialized view definition. Therefore, the following query:
SELECT p.prod_subcategory, t.calendar_month_desc, c.cust_city, AVG(s.amount_sold) FROM sales s, products p, times t, customers c WHERE s.time_id=t.time_id AND s.prod_id=p.prod_id AND s.cust_id=c.cust_id GROUP BY p.prod_subcategory, t.calendar_month_desc, c.cust_city;
This query is rewritten as:
SELECT prod_subcategory, calendar_month_desc, cust_city, sum_amount_sold/count_amount_sold FROM sum_sales_pscat_month_city_mv;
Note that, under the partial text match rewrite method, the average of sales aggregate required by the query is computed using the sum of sales and count of sales aggregates stored in the materialized view.
When neither text match succeeds, the optimizer uses a general query rewrite method.
Text match rewrite can distinguish uppercase from lowercase. For example, the following statement:
SELECT X, 'aBc' FROM Y
This statement matches this statement:
Select x, 'aBc' From y
Text match rewrite can support set operators (UNION ALL, UNION, MINUS, INTERSECT).
Oracle employs a number of checks to determine if a query can be rewritten to use a materialized view. These checks are as follows:
Table 22-1 illustrates how Oracle makes these five checks depending on the type of materialized view. Note that, depending on the composition of the materialized view, some or all of the checks may be made.
To perform these checks, the optimizer uses data relationships on which it can depend. For example, primary key and foreign key relationships tell the optimizer that each row in the foreign key table joins with at most one row in the primary key table. Furthermore, if there is a NOT NULL constraint on the foreign key, it indicates that each row in the foreign key table must join to exactly one row in the primary key table.
Data relationships such as these are very important for query rewrite because they tell what type of result is produced by joins, grouping, or aggregation of data. Therefore, to maximize the rewritability of a large set of queries when such data relationships exist in a database, they should be declared by the user.
To clarify when dimensions and constraints are required for the different types of query rewrite, refer to Table 22-2.
Data warehouse applications recognize multi-dimensional cubes in the database by identifying integrity constraints in the relational schema. Integrity constraints represent primary and foreign key relationships between fact and dimension tables. By querying the data dictionary, applications can recognize integrity constraints and hence the cubes in the database. However, this does not work in an environment where DBAs, for schema complexity or security reasons, define views on fact and dimension tables. In such environments, applications cannot identify the cubes properly. By allowing constraint definitions between views, you can propagate base table constraints to the views, thereby allowing applications to recognize cubes even in a restricted environment.
View constraint definitions are declarative in nature, but operations on views are subject to the integrity constraints defined on the underlying base tables, and constraints on views can be enforced through constraints on base tables. Defining constraints on base tables is necessary, not only for data correctness and cleanliness, but also for materialized view query rewrite purposes using the original base objects.
Materialized view rewrite extensively uses constraints for query rewrite. They are used for determining lossless joins, which, in turn, determine if joins in the materialized view are compatible with joins in the query and thus if rewrite is possible.
DISABLE NOVALIDATE is the only valid state for a view constraint. However, you can choose RELY or NORELY as the view constraint state to enable more sophisticated query rewrites. For example, a view constraint in the RELY state allows query rewrite to occur when the query integrity level is set to ENFORCED. Table 22-3 illustrates when view constraints are used for determining lossless joins.
Note that view constraints cannot be used for query rewrite integrity level TRUSTED. This level enforces the highest degree of constraint enforcement ENABLE VALIDATE.
| Constraint States | RELY | NORELY |
|---|---|---|
|
|
No |
No |
|
|
Yes |
No |
|
|
Yes |
No |
To demonstrate the rewrite capabilities on views, you have to extend the sh sample schema as follows:
CREATE VIEW time_view AS SELECT time_id, TO_NUMBER(TO_CHAR(time_id, 'ddd')) AS day_in_year FROM times;
You can now establish a foreign-primary key relationship (in RELY ON) mode between the view and the fact table, and thus rewrite will take place as described in Table 22-3, by adding the following constraints. Rewrite will then work for example in TRUSTED mode.
ALTER VIEW time_view ADD (CONSTRAINT time_view_pk PRIMARY KEY (time_id) DISABLE NOVALIDATE); ALTER VIEW time_view MODIFY CONSTRAINT time_view_pk RELY; ALTER TABLE sales ADD (CONSTRAINT time_view_fk FOREIGN key (time_id) REFERENCES time_view(time_id) DISABLE NOVALIDATE); ALTER TABLE sales MODIFY CONSTRAINT time_view_fk RELY;
Consider the following materialized view definition:
CREATE MATERIALIZED VIEW sales_pcat_cal_day_mv ENABLE QUERY REWRITE AS SELECT p.prod_category, t.day_in_year, SUM(s.amount_sold) as sum_amount_sold FROM time_view t, sales s, products p WHERE t.time_id = s.time_id AND p.prod_id = s.prod_id GROUP BY p.prod_category, t.day_in_year;
The following query, omitting the dimension table products, will also be rewritten without the primary key/foreign key relationships, because the suppressed join between sales and products is known to be lossless.
SELECT t.day_in_year, SUM(s.amount_sold) AS sum_amount_sold FROM time_view t, sales s WHERE t.time_id = s.time_id GROUP BY t.day_in_year;
However, if the materialized view sales_pcat_cal_day_mv were defined only in terms of the view time_view, then you could not rewrite the following query, suppressing then join between sales and time_view, because there is no basis for losslessness of the delta materialized view join. With the additional constraints as shown previously, this query will also rewrite.
SELECT p.prod_category, SUM(s.amount_sold) AS sum_amount_sold FROM sales s, products p WHERE p.prod_id = s.prod_id GROUP BY p.prod_category;
To revert the changes you have made to the sales history schema, apply the following SQL commands:
ALTER TABLE sales DROP CONSTRAINT time_view_fk; DROP VIEW time_view;
If the referential constraint definition involves a view, that is, either the foreign key or the referenced key resides in a view, the constraint can only be in DISABLE NOVALIDATE mode.
A RELY constraint on a view is allowed only if the referenced UNIQUE or PRIMARY KEY constraint in DISABLE NOVALIDATE mode is also a RELY constraint.
The specification of ON DELETE actions associated with a referential Integrity constraint, is not allowed (for example, DELETE cascade). However, DELETE, UPDATE, and INSERT operations are allowed on views and their base tables as view constraints are in DISABLE NOVALIDATE mode.
An expression that appears in a query can be replaced with a simple column in a materialized view provided the materialized view column represents a precomputed expression that matches with the expression in the query. If a query can be rewritten to use a materialized view, it will be faster. This is because materialized views contain precomputed calculations and do not need to perform expression computation.
The expression matching is done by first converting the expressions into canonical forms and then comparing them for equality. Therefore, two different expressions will be matched as long as they are equivalent to each other. Further, if the entire expression in a query fails to match with an expression in a materialized view, then subexpressions of it are tried to find a match. The subexpressions are tried in a top-down order to get maximal expression matching.
Consider a query that asks for sum of sales by age brackets (1-10, 11-20, 21-30, and so on).
CREATE MATERIALIZED VIEW sales_by_age_bracket_mv ENABLE QUERY REWRITE AS SELECT TO_CHAR((2000-c.cust_year_of_birth)/10-0.5,999) AS age_bracket, SUM(s.amount_sold) AS sum_amount_sold FROM sales s, customers c WHERE s.cust_id=c.cust_id GROUP BY TO_CHAR((2000-c.cust_year_of_birth)/10-0.5,999);
The following query rewrites, using expression matching:
SELECT TO_CHAR(((2000-c.cust_year_of_birth)/10)-0.5,999), SUM(s.amount_sold) FROM sales s, customers c WHERE s.cust_id=c.cust_id GROUP BY TO_CHAR((2000-c.cust_year_of_birth)/10-0.5,999);
This query is rewritten in terms of sum_sales_mv based on the matching of the canonical forms of the age bracket expressions (that is, 2000 - c.cust_year_of_birth)/10-0.5), as follows.
SELECT age_bracket, sum_amount_sold FROM sales_by_age_bracket_mv;
Date folding rewrite is a specific form of expression matching rewrite. In this type of rewrite, a date range in a query is folded into an equivalent date range representing higher date granules. The resulting expressions representing higher date granules in the folded date range are matched with equivalent expressions in a materialized view. The folding of date range into higher date granules such as months, quarters, or years is done when the underlying datatype of the column is an Oracle DATE. The expression matching is done based on the use of canonical forms for the expressions.
DATE is a built-in datatype which represents ordered time units such as seconds, days, and months, and incorporates a time hierarchy (second -> minute -> hour -> day -> month -> quarter -> year). This hard-coded knowledge about DATE is used in folding date ranges from lower-date granules to higher-date granules. Specifically, folding a date value to the beginning of a month, quarter, year, or to the end of a month, quarter, year is supported. For example, the date value 1-jan-1999 can be folded into the beginning of either year 1999 or quarter 1999-1 or month 1999-01. And, the date value 30-sep-1999 can be folded into the end of either quarter 1999-03 or month 1999-09.
Because date values are ordered, any range predicate specified on date columns can be folded from lower level granules into higher level granules provided the date range represents an integral number of higher level granules. For example, the range predicate date_col >= '1-jan-1999' AND date_col < '30-jun-1999' can be folded into either a month range or a quarter range using the TO_CHAR function, which extracts specific date components from a date value.
The advantage of aggregating data by folded date values is the compression of data achieved. Without date folding, the data is aggregated at the lowest granularity level, resulting in increased disk space for storage and increased I/O to scan the materialized view.
Consider a query that asks for the sum of sales by product types for the years 1998.
SELECT p.prod_category, SUM(s.amount_sold) FROM sales s, products p WHERE s.prod_id=p.prod_id AND s.time_id >= TO_DATE('01-jan-1998', 'dd-mon-yyyy') AND s.time_id < TO_DATE('01-jan-1999', 'dd-mon-yyyy') GROUP BY p.prod_category; CREATE MATERIALIZED VIEW sum_sales_pcat_monthly_mv ENABLE QUERY REWRITE AS SELECT p.prod_category, TO_CHAR(s.time_id,'YYYY-MM') AS month, SUM(s.amount_sold) AS sum_amount FROM sales s, products p WHERE s.prod_id=p.prod_id GROUP BY p.prod_category, TO_CHAR(s.time_id, 'YYYY-MM'); SELECT p.prod_category, SUM(s.amount_sold) FROM sales s, products p WHERE s.prod_id=p.prod_id AND TO_CHAR(s.time_id, 'YYYY-MM') >= '01-jan-1998' AND TO_CHAR(s.time_id, 'YYYY-MM') < '01-jan-1999' GROUP BY p.prod_category; SELECT mv.prod_category, mv.sum_amount FROM sum_sales_pcat_monthly_mv mv WHERE month >= '01-jan-1998' AND month < '01-jan-1999';
The range specified in the query represents an integral number of years, quarters, or months. Assume that there is a materialized view mv3 that contains pre-summarized sales by prod_type and is defined as follows:
CREATE MATERIALIZED VIEW mv3 ENABLE QUERY REWRITE AS SELECT prod_type, TO_CHAR(sale_date,'yyyy-mm') AS month, SUM(sales) AS sum_sales FROM fact, product WHERE fact.prod_id = product.prod_id GROUP BY prod_type, TO_CHAR(sale_date, 'yyyy-mm');
The query can be rewritten by first folding the date range into the month range and then matching the expressions representing the months with the month expression in mv3. This rewrite is shown in two steps (first folding the date range followed by the actual rewrite).
SELECT prod_type, SUM(sales) AS sum_sales FROM fact, product WHERE fact.prod_id = product.prod_id AND TO_CHAR(sale_date, 'yyyy-mm') >= TO_CHAR('01-jan-1998', 'yyyy-mm') AND < TO_CHAR('01-jan-1999', 'yyyy-mm') GROUP BY prod_type; SELECT prod_type, sum_sales FROM mv3 WHERE month >= TO_CHAR('01-jan-1998', 'yyyy-mm') AND < TO_CHAR('01-jan-1999', 'yyyy-mm'); GROUP BY prod_type;
If mv3 had pre-summarized sales by prod_type and year instead of prod_type and month, the query could still be rewritten by folding the date range into year range and then matching the year expressions.
Oracle supports rewriting of queries so that they will use materialized views in which the HAVING or WHERE clause of the materialized view contains a selection of a subset of the data in a table or tables. A materialized view's WHERE or HAVING clause can contain a join, a selection, or both, and still be used by a rewritten query. Predicate clauses containing expressions, or selecting rows based on the values of particular columns, are examples of non-join predicates.
To perform this type of query rewrite, Oracle must determine if the data requested in the query is contained in, or is a subset of, the data stored in the materialized view. This problem is sometimes referred to as the data containment problem or, in more general terms, the problem of a restricted subset of data in a materialized view. The following sections detail the conditions where Oracle can solve this problem and thus rewrite a query to use a materialized view that contains a restricted portion of the data in the detail table.
Selection compatibility is performed when both the query and the materialized view contain selections (non-joins). A selection compatibility check is done on the WHERE as well as the HAVING clause. If the materialized view contains selections and the query does not, then selection compatibility check fails because the materialized view is more restrictive than the query. If the query has selections and the materialized view does not then selection compatibility check is not needed. Regardless, selections and any columns mentioned in them must pass the data sufficiency check.
The following definitions are introduced to help the discussion:
Is one of the following (=, <, <=, >, >=)
Is (=, <, <=, >, >=, !=, [NOT] BETWEEN | IN| LIKE |NULL)
Is of the form (column1 join relop column2), where columns are from different tables within the same FROM clause in the current query block. So, for example, there cannot be an outer reference.
Is of the form LHS-expression relop RHS-expression, where LHS means left-hand side and RHS means right-hand side. All non-join predicates are selection predicates. The left-hand side usually contains a column and the right-hand side contains the values. For example, color='red' means the left-hand side is color and the right-hand side is 'red' and the relational operator is (=).
When comparing a selection from the query with a selection from the materialized view, the left-hand side of the selection is compared with the left-hand side of the query. If they match, they are said to be LHS-constrained or just constrained for short.
When comparing a selection from the query with a selection from the materialized view, the right-hand side of the selection is compared with the right-hand side of the query. If they match, they are said to be RHS-constrained or just constrained. Note that before comparing the selections, the LHS/RHS-expression is converted to a canonical form and then the comparison is done. This means that expressions such as column1 + 5 and 5 + column1 will match and be constrained.
Although selection compatibility does not restrict the general form of the WHERE, there is an optimal pattern and normally most queries fall into this pattern as follows:
(join predicate AND join predicate AND ....) AND (selection predicate AND|OR selection predicate .... )
The join compatibility check operates on the joins and the selection compatibility operates on the selections. If the WHERE clause has an OR at the top, then the optimizer first checks for common predicates under the OR. If found, the common predicates are factored out from under the OR then joined with an AND back to the OR. This helps to put the WHERE into the optimal pattern. This is done only if OR occurs at the top of the WHERE clause. For example, if the WHERE clause is:
(sales.prod_id = prod.prod_id AND prod.prod_name = 'Kids Polo Shirt') OR (sales.prod_id = prod.prod_id AND prod.prod_name = 'Kids Shorts')
The join is factored out and the WHERE becomes:
(sales.prod_id = prod.prod_id) AND (prod.prod_name = 'Kids Polo Shirt' OR prod.prod_name = 'Kids Shorts')
Thus putting the WHERE into the most optimal pattern.
If the WHERE is so complex that factoring cannot be done, all predicates under the OR are treated as selections and join compatibility is not performed but selection compatibility is still performed. In the HAVING clause, all predicates are considered selections.
Selection compatibility categorizes selections into the following cases:
Simple selections are of the form expression relop constant.
Complex selections are of the form expression relop expression.
Range selections are of a form such as WHERE (cust_last_name BETWEEN 'abacrombe' AND 'anakin').
Note that simple selections with relational operators (<,<=,>,>=)are also considered range selections.
IN lists
Single and multi-column IN lists such as WHERE(prod_id) IN (102, 233, ....).
Note that selections of the form (column1='v1' OR column1='v2' OR column1='v3' OR ....) are treated as a group and classified as an IN list.
IS [NOT] NULL[NOT] LIKEOther selections are when selection compatibility cannot determine containment of data. For example, EXISTS.
When comparing a selection from the query with a selection from the materialized view, the left-hand side of the selection is compared with the left-hand side of the query. If they match, they are said to be LHS-constrained or constrained for short.
If the selections are constrained, then the right-hand side values are checked for containment. That is, the RHS values of the query selection must be contained by right-hand side values of the materialized view selection.
If the query contains the following:
WHERE prod_id = 102
And if a materialized view contains the following:
WHERE prod_id BETWEEN 0 AND 200
In this example, the selections are constrained on prod_id and the right-hand side value of the query 102 is within the range of the materialized view.
A selection can be a bounded range (a range with an upper and lower value), for example:
If the query contains the following:
WHERE prod_id > 10 AND prod_id < 50
And if a materialized view contains the following:
WHERE prod_id BETWEEN 0 AND 200
In this example, the selections are constrained on prod_id and the query range is within the materialized view range. In this example, we notice that both query selections are constrained by the same materialized view selection. The left-hand side can be an expression.
If the query contains the following:
WHERE (sales.amount_sold * .07) BETWEEN 1.00 AND 100.00
And if a materialized view contains the following:
WHERE (sales.amount_sold * .07) BETWEEN 0.0 AND 200.00
In this example, the selections are constrained on (sales.amount_sold *.07) and the right-hand side value of the query is within the range of the materialized view. Complex selections require that both the left-hand side and right-hand side be matched (for example, when the left-hand side and the right-hand side are constrained).
If the query contains the following:
WHERE (cost.unit_price * 0.95) > (cost_unit_cost * 1.25)
And if a materialized view contains the following:
WHERE (cost.unit_price * 0.95) > (cost_unit_cost * 1.25)
If the left-hand side and the right-hand side are constrained and the <selection relop> is the same, then generally the selection can be dropped from the rewritten query. Otherwise, the selection must be keep to filter out extra data from the materialized view.
If query rewrite can drop the selection from the rewritten query, then any columns from the selection may not have to be in the materialized view so more rewrites can be done with less data.
Selection compatibility requires that all selections in the materialized view be LHS-constrained with some selection in the query. This ensures that the materialized view data is not more restrictive that the query.
Selections in the query do not have to be constrained by any selections in the materialized view but if they are then the right-hand side values must be contained by the materialized view. For example,
If the query contains the following:
WHERE prod_name = 'Shorts' AND prod_category = 'Men'
And if a materialized view contains the following:
WHERE prod_category = 'Men'
In this example, selection with prod_category is constrained. The query has an extra selection that is not constrained but this is acceptable because the materialized view does have the data.
If the query contains the following:
WHERE prod_category = 'Men'
And if a materialized view contains the following:
WHERE prod_name = 'Shorts' AND prod_category = 'Men'
In this example, the materialized view selection with prod_name is not constrained. The materialized view is more restrictive that the query because it only contains the product Shorts, therefore, query rewrite will not occur.
Selection compatibility also checks for cases where the query has a multi-column in list where the columns are fully constrained by individual columns from the materialized view single column in lists. For example:
If the query contains the following:
WHERE (prod_id, cust_id) IN ((1022, 1000), (1033, 2000))
And if a materialized view contains the following:
WHERE prod_id IN (1022,1033) AND cust_id IN (1000, 2000)
In this example, the materialized view IN lists are constrained by the columns in the query multi-column in list. Furthermore, the right-hand side values of the query selection are contained by the materialized view so that rewrite will occur.
Selection compatibility also checks for cases where the materialized view has a multi-column IN-list where the columns are fully constrained by individual columns or columns from IN-lists in the query. For example:
If the query contains the following:
WHERE prod_id = 1022 AND cust_id IN (1000, 2000)
And if a materialized view contains the following:
WHERE (prod_id, cust_id) IN ((1022, 1000), (1022, 2000))
In this example, the materialized view IN-list columns are fully constrained by the columns in the query selections. Furthermore, the right-hand side values of the query selection are contained by the materialized view. However, the following example fails selection compatibility check.
If the query contains the following:
WHERE (prod_id = 1022 AND cust_id IN (1000, 2000)
And if a materialized view contains the following:
WHERE (prod_id, cust_id, cust_city) IN ((1022, 1000, 'Boston'), (1022, 2000, 'Nashua'))
In this example, the materialized view in list column cust_city is not constrained so the materialized view is more restrictive than the query. Selection compatibility also works with complex ORs. If we assume that the shape of the WHERE is as follows:
(selection AND selection AND ...) OR (selection AND selection AND ...)
Each group of selections separated by AND is related and the group is called a disjunct. The disjuncts are separated by ORs. Selection compatibility requires that every disjunct in the query be contained by some disjunct in the materialized view. Otherwise, the materialized view is more restrictive than the query. The materialized view disjuncts do not have to match any query disjunct. This just means that the materialized view has more data than the query requires. When comparing a disjunct from the query with a disjunct of the materialized view, the normal selection compatibility rules apply as specified in the previous discussion. For example:
If the query contains the following:
WHERE (city_population > 15000 AND city_population < 25000 AND state_name = 'New Hampshire')
And if a materialized view contains the following:
WHERE (city_population < 5000 AND state_name = 'New York') OR (city_population BETWEEN 10000 AND 50000 AND state_name = 'New Hampshire')
In this example, the query has a single disjunct (group of selections separated by AND). The materialized view has two disjuncts separated by OR. The query disjunct is contained by the second materialized view disjunct so selection compatibility succeeds. It is clear that the materialized view contains more data than needed by the query so the query can be rewritten.
For example, here is a simple materialized view definition:
CREATE MATERIALIZED VIEW cal_month_sales_id_mv BUILD IMMEDIATE REFRESH FORCE ENABLE QUERY REWRITE AS SELECT t.calendar_month_desc, SUM(s.amount_sold) AS dollars FROM sales s, times t WHERE s.time_id = t.time_id AND s.cust_id = 10 GROUP BY t.calendar_month_desc;
The following query could be rewritten to use this materialized view because the query asks for the amount where the customer ID is 10 and this is contained in the materialized view.
SELECT t.calendar_month_desc, SUM(s.amount_sold) AS dollars FROM times t, sales s WHERE s.time_id = t.time_id AND s.cust_id = 10 GROUP BY t.calendar_month_desc;
Because the predicate s.cust_id = 10 selects the same data in the query and in the materialized view, it is dropped from the rewritten query. This means the rewritten query looks like:
SELECT mv.calendar_month_desc, mv.dollars FROM cal_month_sales_id_mv mv;
Query rewrite can also occur when the query specifies a range of values, such as s.prod_id > 10000 and s.prod_id < 20000, as long as the range specified in the query is within the range specified in the materialized view. For example, if there is a materialized view defined as:
CREATE MATERIALIZED VIEW product_sales_mv BUILD IMMEDIATE REFRESH FORCE ENABLE QUERY REWRITE AS SELECT p.prod_name, SUM(s.amount_sold) AS dollar_sales FROM products p, sales s WHERE p.prod_id = s.prod_id GROUP BY prod_name HAVING SUM(s.amount_sold) BETWEEN 5000 AND 50000;
Then a query such as:
SELECT p.prod_name, SUM(s.amount_sold) AS dollar_sales FROM products p, sales s WHERE p.prod_id = s.prod_id GROUP BY prod_name HAVING SUM(s.amount_sold) BETWEEN 10000 AND 20000;
This query would be rewritten as follows:
SELECT prod_name, dollar_sales FROM product_sales_mv WHERE dollar_sales > 10000 AND dollar_sales < 20000;
Rewrite with select expressions is also supported when the expression evaluates to a constant, such as TO_DATE('12-SEP-1999','DD-Mon-YYYY'). For example, if an existing materialized view is defined as:
CREATE MATERIALIZED VIEW sales_on_valentines_day_99_mv BUILD IMMEDIATE REFRESH FORCE ENABLE QUERY REWRITE AS SELECT prod_id, cust_id, amount_sold FROM sales s, times t WHERE s.time_id = t.time_id AND t.time_id = TO_DATE('04-FEB-1999', 'DD-MON-YYYY');
Then the following query:
SELECT prod_id, cust_id, amount_sold FROM sales s, times t WHERE s.time_id = t.time_id AND t.time_id = TO_DATE('14-FEB-1999', 'DD-MON-YYYY');
This query would be rewritten as follows:
SELECT * FROM sales_on_valentines_day_99_mv;
Rewrite can also occur against a materialized view when the selection is contained in an IN expression. For example, given the following materialized view definition:
CREATE MATERIALIZED VIEW popular_promo_sales_mv BUILD IMMEDIATE REFRESH FORCE ENABLE QUERY REWRITE AS SELECT p.promo_name, SUM(s.amount_sold) AS sum_amount_sold FROM promotions p, sales s WHERE s.promo_id = p.promo_id AND promo_name IN ('coupon', 'premium', 'giveaway') GROUP BY promo_name;
The following query:
SELECT p.promo_name, SUM(s.amount_sold) FROM promotions p, sales s WHERE s.promo_id = p.promo_id AND promo_name IN ('coupon', 'premium') GROUP BY promo_name;
This query is rewritten as follows:
SELECT * FROM popular_promo_sales_mv WHERE promo_name IN ('coupon', 'premium');
You can also use expressions in selection predicates. This process looks like the following example:
expression relational operator constant
where expression can be any arbitrary arithmetic expression allowed by Oracle. The expression in the materialized view and the query must match. Oracle attempts to discern expressions that are logically equivalent, such as A+B and B+A, and will always recognize identical expressions as being equivalent.
You can also use queries with an expression on both sides of the operator or user-defined functions as operators. Query rewrite occurs when the complex predicate in the materialized view and the query are logically equivalent. This means that, unlike exact text match, terms could be in a different order and rewrite can still occur, as long as the expressions are equivalent.
In addition, selection predicates can be joined with an AND operator in a query and the query can still be rewritten to use a materialized view as long as every restriction on the data selected by the query is matched by a restriction in the definition of the materialized view. Again, this does not mean an exact text match, but that the restrictions on the data selected must be a logical match. Also, the query may be more restrictive in its selection of data and still be eligible, but it can never be less restrictive than the definition of the materialized view and still be eligible for rewrite.
For example, given the preceding materialized view definition, a query such as:
SELECT p.promo_name, SUM(s.amount_sold) FROM promotions p, sales s WHERE s.promo_id = p.promo_id AND promo_name = 'coupon' GROUP BY promo_name HAVING SUM(s.amount_sold) > 1000;
This query would be rewritten as follows:
SELECT * FROM popular_promo_sales_mv WHERE promo_name = 'coupon' AND sum_amount_sold > 1000;
This is an example where the query is more restrictive than the definition of the materialized view, so rewrite can occur. However, if the query had selected promo_category, then it could not have been rewritten against the materialized view, because the materialized view definition does not contain that column.
For another example, if the definition of a materialized view restricts a city name column to Boston, then a query that selects Seattle as a value for this column can never be rewritten with that materialized view, but a query that restricts city name to Boston and restricts a column value that is not restricted in the materialized view could be rewritten to use the materialized view.
All the rules noted previously also apply when predicates are combined with an OR operator. The simple predicates, or simple predicates connect by ANDs, are considered separately. Each predicate in the query must appear in the materialized view if rewrite is to occur.
For example, the query could have a restriction like city='Boston' OR city ='Seattle' and to be eligible for rewrite, the materialized view that the query might be rewritten against must have the same restriction. In fact, the materialized view could have additional restrictions, such as city='Boston' OR city='Seattle' OR city='Cleveland' and rewrite might still be possible.
Note, however, that the reverse is not true. If the query had the restriction city = 'Boston' OR city='Seattle' OR city='Cleveland' and the materialized view only had the restriction city='Boston' OR city='Seattle', then rewrite would not be possible since the query seeks more data than is contained in the restricted subset of data stored in the materialized view.
In this check, the joins in a query are compared against the joins in a materialized view. In general, this comparison results in the classification of joins into three categories:
These can be visualized as shown in Figure 22-2.
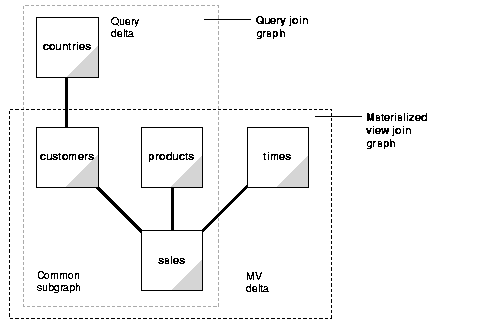
The common join pairs between the two must be of the same type, or the join in the query must be derivable from the join in the materialized view. For example, if a materialized view contains an outer join of table A with table B, and a query contains an inner join of table A with table B, the result of the inner join can be derived by filtering the anti-join rows from the result of the outer join.
For example, consider the following query:
SELECT p.prod_name, t.week_ending_day, SUM(amount_sold) FROM sales s, products p, times t WHERE s.time_id=t.time_id AND s.prod_id = p.prod_id AND t. week_ending_day BETWEEN TO_DATE('01-AUG-1999', 'DD-MON-YYYY') AND TO_DATE('10-AUG-1999', 'DD-MON-YYYY') GROUP BY prod_name, week_ending_day;
The common joins between this query and the materialized view join_sales_time_product_mv are:
s.time_id = t.time_id AND s.prod_id = p.prod_id
They match exactly and the query can be rewritten as follows:
SELECT prod_name, week_ending_day, SUM(amount_sold) FROM join_sales_time_product_mv WHERE week_ending_day BETWEEN TO_DATE('01-AUG-1999','DD-MON-YYYY') AND TO_DATE('10-AUG-1999','DD-MON-YYYY') GROUP BY prod_name, week_ending_day;
The query could also be answered using the join_sales_time_product_oj_mv materialized view where inner joins in the query can be derived from outer joins in the materialized view. The rewritten version will (transparently to the user) filter out the anti-join rows. The rewritten query will have the following structure:
SELECT prod_name, week_ending_day, SUM(amount_sold) FROM join_sales_time_product_oj_mv WHERE week_ending_day BETWEEN TO_DATE('01-AUG-1999','DD-MON-YYYY') AND TO_DATE('10-AUG-1999','DD-MON-YYYY') AND prod_id IS NOT NULL GROUP BY prod_name, week_ending_day;
In general, if you use an outer join in a materialized view containing only joins, you should put in the materialized view either the primary key or the rowid on the right side of the outer join. For example, in the previous example, join_sales_time_product_oj_mv, there is a primary key on both sales and products.
Another example of when a materialized view containing only joins is used is the case of a semi-join rewrites. That is, a query contains either an EXISTS or an IN subquery with a single table.
Consider this query, which reports the products that had sales greater than $1,000.
SELECT DISTINCT prod_name FROM products p WHERE EXISTS (SELECT * FROM sales s WHERE p.prod_id=s.prod_id AND s.amount_sold > 1000);
This query could also be seen as:
SELECT DISTINCT prod_name FROM products p WHERE p.prod_id IN (SELECT s.prod_id FROM sales s WHERE s.amount_sold > 1000 );
This query contains a semi-join between the products and the sales table:
s.prod_id = p.prod_id
This query can be rewritten to use either the join_sales_time_product_mv materialized view, if foreign key constraints are active or join_sales_time_product_oj_mv materialized view, if primary keys are active. Observe that both materialized views contain s.prod_id=p.prod_id, which can be used to derive the semi-join in the query.
The query is rewritten with join_sales_time_product_mv as follows:
SELECT prod_name FROM (SELECT DISTINCT prod_name FROM join_sales_time_product_mv WHERE amount_sold > 1000 );
If the materialized view join_sales_time_product_mv is partitioned by time_id, then this query is likely to be more efficient than the original query because the original join between sales and products has been avoided.
The query could be rewritten using join_sales_time_product_oj_mv as follows.
SELECT prod_name FROM (SELECT DISTINCT prod_name FROM join_sales_time_product_oj_mv WHERE amount_sold > 1000 AND prod_id IS NOT NULL );
Rewrites with semi-joins are currently restricted to materialized views with joins only and are not available for materialized views with joins and aggregates.
A query delta join is a join that appears in the query but not in the materialized view. Any number and type of delta joins in a query are allowed and they are simply retained when the query is rewritten with a materialized view. Upon rewrite, the materialized view is joined to the appropriate tables in the query delta.
For example, consider the following query:
SELECT p.prod_name, t.week_ending_day, c.cust_city, SUM(s.amount_sold) FROM sales s, products p, times t, customers c WHERE s.time_id=t.time_id AND s.prod_id = p.prod_id AND s.cust_id = c.cust_id GROUP BY prod_name, week_ending_day, cust_city;
Using the materialized view join_sales_time_product_mv, common joins are: s.time_id=t.time_id and s.prod_id=p.prod_id. The delta join in the query is s.cust_id=c.cust_id.
The rewritten form will then join the join_sales_time_product_mv materialized view with the customers table as follows:
SELECT mv.prod_name, mv.week_ending_day, c.cust_city, SUM(mv.amount_sold) FROM join_sales_time_product_mv mv, customers c WHERE mv.cust_id = c.cust_id GROUP BY prod_name, week_ending_day, cust_city;
A materialized view delta join is a join that appears in the materialized view but not the query. All delta joins in a materialized view are required to be lossless with respect to the result of common joins. A lossless join guarantees that the result of common joins is not restricted. A lossless join is one where, if two tables called A and B are joined together, rows in table A will always match with rows in table B and no data will be lost, hence the term lossless join. For example, every row with the foreign key matches a row with a primary key provided no nulls are allowed in the foreign key. Therefore, to guarantee a lossless join, it is necessary to have FOREIGN KEY, PRIMARY KEY, and NOT NULL constraints on appropriate join keys. Alternatively, if the join between tables A and B is an outer join (A being the outer table), it is lossless as it preserves all rows of table A.
All delta joins in a materialized view are required to be non-duplicating with respect to the result of common joins. A non-duplicating join guarantees that the result of common joins is not duplicated. For example, a non-duplicating join is one where, if table A and table B are joined together, rows in table A will match with at most one row in table B and no duplication occurs. To guarantee a non-duplicating join, the key in table B must be constrained to unique values by using a primary key or unique constraint.
Consider the following query that joins sales and times:
SELECT t.week_ending_day, SUM(s.amount_sold) FROM sales s, times t WHERE s.time_id = t.time_id AND t.week_ending_day BETWEEN TO_DATE('01-AUG-1999', 'DD-MON-YYYY') AND TO_DATE('10-AUG-1999', 'DD-MON-YYYY') GROUP BY week_ending_day;
The materialized view join_sales_time_product_mv has an additional join (s.prod_id=p.prod_id) between sales and products. This is the delta join in join_sales_time_product_mv. You can rewrite the query if this join is lossless and non-duplicating. This is the case if s.prod_id is a foreign key to p.prod_id and is not null. The query is therefore rewritten as:
SELECT week_ending_day, SUM(amount_sold) FROM join_sales_time_product_mv WHERE week_ending_day BETWEEN TO_DATE('01-AUG-1999', 'DD-MON-YYYY') AND TO_DATE('10-AUG-1999', 'DD-MON-YYYY') GROUP BY week_ending_day;
The query can also be rewritten with the materialized view join_sales_time_product_mv_oj where foreign key constraints are not needed. This view contains an outer join (s.prod_id=p.prod_id(+)) between sales and products. This makes the join lossless. If p.prod_id is a primary key, then the non-duplicating condition is satisfied as well and optimizer will rewrite the query as follows:
SELECT week_ending_day, SUM(amount_sold) FROM join_sales_time_product_oj_mv WHERE week_ending_day BETWEEN TO_DATE('01-AUG-1999', 'DD-MON-YYYY') AND TO_DATE('10-AUG-1999', 'DD-MON-YYYY') GROUP BY week_ending_day;
Note that the outer join in the definition of join_sales_time_product_mv_oj is not necessary, because the parent key - foreign key relationship between sales and products in the Sales History schema is already lossless. It is used for demonstration purposes only, and would be necessary if sales.prod_id is nullable, thus violating the losslessness of the join condition sales.prod_id = products.prod_id.
Current limitations restrict most rewrites with outer joins to materialized views with joins only. There is limited support for rewrites with materialized aggregate views with outer joins, so those views should rely on foreign key constraints to assure losslessness of materialized view delta joins.
Query rewrite is able to make many transformations based upon the recognition of equivalent joins. Query rewrite recognizes the following construct as being equivalent to a join:
WHERE table1.column1 = F(args) /* sub-expression A */ AND table2.column2 = F(args) /* sub-expression B */
If F(args) is a PL/SQL function that is declared to be deterministic and the arguments to both invocations of F are the same, then the combination of sub-expression A with sub-expression B be can be recognized as a join between table1.column1 and table2.column2. That is, the following expression is equivalent to the previous expression:
WHERE table1.column1 = F(args) /* sub-expression A */ AND table2.column2 = F(args) /* sub-expression B */ AND table1.column1 = table2.column2 /* join-expression J */
Because join-expression J can be inferred from sub-expression A and sub-expression B, the inferred join can be used to match a corresponding join of table1.column1 = table2.column2 in a materialized view.
In this check, the optimizer determines if the necessary column data requested by a query can be obtained from a materialized view. For this, the equivalence of one column with another is used. For example, if an inner join between table A and table B is based on a join predicate A.X = B.X, then the data in column A.X will equal the data in column B.X in the result of the join. This data property is used to match column A.X in a query with column B.X in a materialized view or vice versa. For example, consider this query:
SELECT p.prod_name, s.time_id, t.week_ending_day, SUM(s.amount_sold) FROM sales s, products p, times t WHERE s.time_id=t.time_id AND s.prod_id = p.prod_id GROUP BY p.prod_name, s.time_id, t.week_ending_day;
This query can be answered with join_sales_time_product_mv even though the materialized view does not have s.time_id. Instead, it has t.time_id, which, through a join condition s.time_id=t.time_id, is equivalent to s.time_id.
Thus, the optimizer might select this rewrite:
SELECT prod_name, time_id, week_ending_day, SUM(amount_sold) FROM join_sales_time_product_mv GROUP BY prod_name, time_id, week_ending_day;
If some column data requested by a query cannot be obtained from a materialized view, the optimizer further determines if it can be obtained based on a data relationship called functional dependency. When the data in a column can determine data in another column, such a relationship is called functional dependency or functional determinance. For example, if a table contains a primary key column called prod_id and another column called prod_name, then, given a prod_id value, it is possible to look up the corresponding prod_name. The opposite is not true, which means a prod_name value need not relate to a unique prod_id.
When the column data required by a query is not available from a materialized view, such column data can still be obtained by joining the materialized view back to the table that contains required column data provided the materialized view contains a key that functionally determines the required column data.
For example, consider the following query:
SELECT p.prod_category, t.week_ending_day, SUM(s.amount_sold) FROM sales s, products p, times t WHERE s.time_id=t.time_id AND s.prod_id=p.prod_id AND p.prod_category='CD' GROUP BY p.prod_category, t.week_ending_day;
The materialized view sum_sales_prod_week_mv contains p.prod_id, but not p.prod_category. However, we can join sum_sales_prod_week_mv back to products to retrieve prod_category because prod_id functionally determines prod_category. The optimizer rewrites this query using sum_sales_prod_week_mv as follows:
SELECT p.prod_category, mv.week_ending_day, SUM(mv.sum_amount_sold) FROM sum_sales_prod_week_mv mv, products p WHERE mv.prod_id=p.prod_id AND p.prod_category='CD' GROUP BY p.prod_category, mv.week_ending_day;
Here the products table is called a joinback table because it was originally joined in the materialized view but joined again in the rewritten query.
There are two ways to declare functional dependency:
DETERMINES clause of a dimensionThe DETERMINES clause of a dimension definition might be the only way you could declare functional dependency when the column that determines another column cannot be a primary key. For example, the products table is a denormalized dimension table that has columns prod_id, prod_name, and prod_subcategory, and prod_subcategory functionally determines prod_subcat_desc and prod_category determines prod_cat_desc.
The first functional dependency can be established by declaring prod_id as the primary key, but not the second functional dependency because the prod_subcategory column contains duplicate values. In this situation, you can use the DETERMINES clause of a dimension to declare the second functional dependency.
The following dimension definition illustrates how the functional dependencies are declared:
CREATE DIMENSION products_dim LEVEL product IS (products.prod_id) LEVEL subcategory IS (products.prod_subcategory) LEVEL category IS (products.prod_category) HIERARCHY prod_rollup ( product CHILD OF subcategory CHILD OF category ) ATTRIBUTE product DETERMINES products.prod_name ATTRIBUTE product DETERMINES products.prod_desc ATTRIBUTE subcategory DETERMINES products.prod_subcat_desc ATTRIBUTE category DETERMINES products.prod_cat_desc;
The hierarchy prod_rollup declares hierarchical relationships that are also 1:n functional dependencies. The 1:1 functional dependencies are declared using the DETERMINES clause, as seen when prod_subcategory functionally determines prod_subcat_desc.
Consider the following query:
SELECT p.prod_subcat_desc, t.week_ending_day, SUM(s.amount_sold) FROM sales s, products p, times t WHERE s.time_id=t.time_id AND s.prod_id=p.prod_id AND p.prod_subcat_desc LIKE '%Men' GROUP BY p.prod_subcat_desc, t.week_ending_day;
This can be rewritten by joining sum_sales_pscat_week_mv to the products table so that prod_subcat_desc is available to evaluate the predicate. But the join will be based on the prod_subcategory column, which is not a primary key in the products table; therefore, it allows duplicates. This is accomplished by using an inline view that selects distinct values and this view is joined to the materialized view as shown in the rewritten query.
SELECT iv.prod_subcat_desc, mv.week_ending_day, SUM(mv.sum_amount_sold) FROM sum_sales_pscat_week_mv mv, (SELECT DISTINCT prod_subcategory, prod_subcat_desc FROM products) iv WHERE mv.prod_subcategory=iv.prod_subcategory AND iv.prod_subcat_desc LIKE '%Men' GROUP BY iv.prod_subcat_desc, mv.week_ending_day;
This type of rewrite is possible because of the fact that prod_subcategory functionally determines prod_subcat_desc as declared in the dimension.
This check is required only if both the materialized view and the query contain a GROUP BY clause. The optimizer first determines if the grouping of data requested by a query is exactly the same as the grouping of data stored in a materialized view. In other words, the level of grouping is the same in both the query and the materialized view.
If the grouping of data requested by a query is at a coarser level compared to the grouping of data stored in a materialized view, the optimizer can still use the materialized view to rewrite the query. For example, the materialized view sum_sales_pscat_week_mv groups by week_ending_day, and prod_subcategory. This query groups by prod_subcategory, a coarser grouping granularity:
SELECT p.prod_subcategory, SUM(s.amount_sold) AS sum_amount FROM sales s, products p WHERE s.prod_id=p.prod_id GROUP BY p.prod_subcategory;
Therefore, the optimizer will rewrite this query as:
SELECT p.prod_subcategory, SUM(sum_amount_sold) FROM sum_sales_pscat_week_mv mv, GROUP BY p.prod_subcategory;
In another example, a query requests data grouped by prod_category whereas a materialized view stores data grouped by prod_subcategory. If prod_subcategory is a CHILD OF prod_category (see the dimension example earlier), the grouped data stored in the materialized view can be further grouped by prod_category when the query is rewritten. In other words, aggregates at prod_subcategory level (finer granularity) stored in a materialized view can be rolled up into aggregates at prod_category level (coarser granularity).
For example, consider the following query:
SELECT p.prod_category, t.week_ending_day, SUM(s.amount_sold) AS sum_amount FROM sales s, products p, times t WHERE s.time_id=t.time_id AND s.prod_id=p.prod_id GROUP BY p.prod_category, t.week_ending_day;
Because prod_subcategory functionally determines prod_category, sum_sales_pscat_week_mv can be used with a joinback to products to retrieve prod_category column data, and then aggregates can be rolled up to prod_category level, as shown here:
SELECT pv.prod_subcategory, mv.week_ending_day, SUM(mv.sum_amount_sold) FROM sum_sales_pscat_week_mv mv, (SELECT DISTINCT prod_subcategory, prod_category FROM products) pv WHERE mv.prod_subcategory=mv.prod_subcategory GROUP BY pv.prod_subcategory, mv.week_ending_day;
Note that, for this rewrite, the data sufficiency check determines that a joinback to the products table is necessary, and the grouping compatibility check determines that aggregate rollup is necessary.
This check is required only if both the query and the materialized view contain aggregates. Here the optimizer determines if the aggregates requested by a query can be derived or computed from one or more aggregates stored in a materialized view. For example, if a query requests AVG(X) and a materialized view contains SUM(X) and COUNT(X), then AVG(X) can be computed as SUM(X)/COUNT(X).
If the grouping compatibility check determined that the rollup of aggregates stored in a materialized view is required, then the aggregate computability check determines if it is possible to roll up each aggregate requested by the query using aggregates in the materialized view.
For example, SUM(sales) at the city level can be rolled up to SUM(sales) at the state level by summing all SUM(sales) aggregates in a group with the same state value. However, AVG(sales) cannot be rolled up to a coarser level unless COUNT(sales) is also available in the materialized view. Similarly, VARIANCE(sales) or STDDEV(sales) cannot be rolled up unless COUNT(sales) and SUM(sales) are also available in the materialized view. For example, given the query:
SELECT p.prod_subcategory, AVG(s.amount_sold) AS avg_sales FROM sales s, products p WHERE s.prod_id = p.prod_id GROUP BY p.prod_subcategory;
This statement can be rewritten with materialized view sum_sales_pscat_month_city_mv provided the join between sales and times and sales and customers are lossless and non-duplicating. Further, the query groups by prod_subcategory whereas the materialized view groups by prod_subcategory, calendar_month_desc and cust_city, which means the aggregates stored in the materialized view will have to be rolled up. The optimizer will rewrite the query as:
SELECT mv.prod_subcategory, SUM(mv.sum_amount_sold)/COUNT(mv.count_amount_sold) AS avg_sales FROM sum_sales_pscat_month_city_mv mv GROUP BY mv.prod_subcategory;
The argument of an aggregate such as SUM can be an arithmetic expression like A+B. The optimizer will try to match an aggregate SUM(A+B) in a query with an aggregate SUM(A+B) or SUM(B+A) stored in a materialized view. In other words, expression equivalence is used when matching the argument of an aggregate in a query with the argument of a similar aggregate in a materialized view. To accomplish this, Oracle converts the aggregate argument expression into a canonical form such that two different but equivalent expressions convert into the same canonical form. For example, A*(B-C), A*B-C*A, (B-C)*A, and -A*C+A*B all convert into the same canonical form and, therefore, they are successfully matched.
Oracle supports general query rewrite when the user query contains an inline view, or a subquery in the FROM list. Query rewrite matches inline views in the materialized view with inline views in the request query when the text of the two inline views exactly match. In this case, rewrite treats the matching inline view as it would a named view, and general rewrite processing is possible.
Here is an example where the materialized view contains an inline view, and the query has the same inline view, but the aliases for these views are different. Previously, this query could not be rewritten because neither exact text match nor partial text match is possible.
Here is the materialized view definition:
CREATE MATERIALIZED VIEW inline_example ENABLE QUERY REWRITE AS SELECT t.calendar_month_name, t.calendar_year p.prod_category, SUM(V1.revenue) AS sum_revenue FROM times t, products p, (SELECT time_id, prod_id, amount_sold*0.2 as revenue FROM sales) V1 WHERE t.time_id = V1.time_id AND p.prod_id = V1.prod_id GROUP BY calendar_month_name, calendar_year, prod_category ;
And here is the query that will be rewritten to use the materialized view:
SELECT t.calendar_month_name, t.calendar_year, p.prod_category, SUM(X1.revenue) AS sum_revenue FROM times t, products p, (SELECT time_id, prod_id, amount_sold*0.2 AS revenue FROM sales) X1 WHERE t.time_id = X1.time_id AND p.prod_id = X1.prod_id GROUP BY calendar_month_name, calendar_year, prod_category ;
Query rewrite of queries which contain multiple references to the same tables, or self joins are possible, to the extent that general rewrite can occur when the query and the materialized view definition have the same aliases for the multiple references to a table. This allows Oracle to provide a distinct identity for each table reference and this in turn allows query rewrite.
The following is an example of a materialized view and a query. In this example, the query is missing a reference to a column in a table so an exact text match will not work. But general query rewrite can occur because the aliases for the table references match.
To demonstrate the self-join rewriting possibility with the Sales History schema, we are assuming the following addition to include the actual shipping and payment date in the fact table, referencing the same dimension table times. This is for demonstration purposes only and will not return any results:
ALTER TABLE sales ADD (time_id_ship DATE); ALTER TABLE sales ADD (CONSTRAINT time_id_book_fk FOREIGN key (time_id_ship) REFERENCES times(time_id) ENABLE NOVALIDATE); ALTER TABLE sales MODIFY CONSTRAINT time_id_book_fk RELY; ALTER TABLE sales ADD (time_id_paid DATE); ALTER TABLE sales ADD (CONSTRAINT time_id_paid_fk FOREIGN key (time_id_paid) REFERENCES times(time_id) ENABLE NOVALIDATE); ALTER TABLE sales MODIFY CONSTRAINT time_id_paid_fk RELY;
To reverse the changes, you can simply drop the columns:
ALTER TABLE sales DROP COLUMN time_id_ship; ALTER TABLE sales DROP COLUMN time_id_paid;
Now, we can define a materialized view as follows:
CREATE MATERIALIZED VIEW sales_shipping_lag_mv ENABLE QUERY REWRITE AS SELECT t1.fiscal_week_number, s.prod_id, t2.fiscal_week_number - t1.fiscal_week_number as lag FROM times t1, sales s, times t2 WHERE t1.time_id = s.time_id AND t2.time_id = s.time_id_ship;
The following query fails the exact text match test but is rewritten because the aliases for the table references match:
SELECT s.prod_id, t2.fiscal_week_number - t1.fiscal_week_number AS lag FROM times t1, sales s, times t2 WHERE t1.time_id = s.time_id AND t2.time_id = s.time_id_ship;
Note that Oracle performs other checks to insure the correct match of an instance of a multiply instanced table in the request query with the corresponding table instance in the materialized view. For instance, in the following example, Oracle correctly determines that the matching alias names used for the multiple instances of table time does not establish a match between the multiple instances of table time in the materialized view:
The following query cannot be rewritten using sales_shipping_lag_mv even though the alias names of the multiply instanced table time match because the joins are not compatible between the instances of time aliased by t2:
SELECT s.prod_id, t2.fiscal_week_number - t1.fiscal_week_number AS lag FROM times t1, sales s, times t2 WHERE t1.time_id = s.time_id AND t2.time_id = s.time_id_paid;
This request query joins the instance of the time table aliased by t2 on the s.time_id_paid column, while the materialized views joins the instance of the time table aliased by t2 on the s.time_id_ship column. Because the join conditions differ, Oracle correctly determines that rewrite cannot occur.
There are a few special cases when using query rewrite:
In Oracle9i, when a certain partition of the detail table is updated, only specific sections of the materialized view are marked stale. The materialized view must have information that can identify the partition of the table corresponding to a particular row or group of the materialized view. The simplest scenario is when the partitioning key of the table is available in the SELECT list of the materialized view because this is the easiest way to map a row to a stale partition. The key points when using partially stale materialized views are:
ENFORCED or TRUSTED mode if the rows from the materialized view used to answer the query are known to be FRESH.WHERE clause. We will rewrite a query with this materialized view if its answer is contained within this (restricted) materialized view. Note that support for materialized views with selection predicates is a prerequisite for this type of rewrite.The fact table sales is partitioned based on ranges of time_id as follows:
PARTITION BY RANGE (time_id) (PARTITION SALES_Q1_1998 VALUES LESS THAN (TO_DATE('01-APR-1998', 'DD-MON-YYYY')), PARTITION SALES_Q2_1998 VALUES LESS THAN (TO_DATE('01-JUL-1998', 'DD-MON-YYYY')), PARTITION SALES_Q3_1998 VALUES LESS THAN (TO_DATE('01-OCT-1998', 'DD-MON-YYYY')), ...
Suppose you have a materialized view grouping by time_id as follows:
CREATE MATERIALIZED VIEW sum_sales_per_city_mv ENABLE QUERY REWRITE AS SELECT s.time_id, p.prod_subcategory, c.cust_city, SUM(s.amount_sold) AS sum_amount_sold FROM sales s, products p, customers c WHERE s.cust_id = c.cust_id AND s.prod_id = p.prod_id GROUP BY time_id, prod_subcategory, cust_city;
Suppose new data will be inserted for December 2000, which will end up in the partition sales_q4_2000. For testing purposes, you can apply an arbitrary DML operation on sales, changing a different partition than sales_q1_2000 when this materialized view is fresh. For example:
INSERT INTO SALES VALUES(10,10,'01-dec-2000','S',10,123.45,54321);
Until a refresh is done, the materialized view is generically stale and cannot be used for unlimited rewrite in enforced mode. However, because the table sales is partitioned and not all partitions have been modified, Oracle can identify all partitions that have not been touched. The fresh rows in the materialized view, that means the data of all partitions where Oracle knows that no changes have occurred, can be represented by modifying the materialized view's defining query as follows:
SELECT s.time_id, p.prod_subcategory, c.cust_city, SUM(s.amount_sold) AS sum_amount_sold FROM sales s, products p, customers c WHERE s.cust_id = c.cust_id AND s.prod_id = p.prod_id AND s.time_id < TO_DATE('01-OCT-2000','DD-MON-YYYY') GROUP BY time_id, prod_subcategory, cust_city;
Note that the freshness of partially stale materialized views is tracked on a per partition base, and not on a logical base. Since the partitioning strategy of the sales fact table is on a quarterly base, changes in December 2000 causes the complete partition sales_q4_2000 to become stale.
Consider the following query which asks for sales in quarter 1 and 2 of 2000:
SELECT s.time_id, p.prod_subcategory, c.cust_city, SUM(s.amount_sold) AS sum_amount_sold FROM sales s, products p, customers c WHERE s.cust_id = c.cust_id AND s.prod_id = p.prod_id AND s.time_id BETWEEN TO_DATE('01-JAN-2000', 'DD-MON-YYYY') AND TO_DATE('01-JUL-2000', 'DD-MON-YYYY') GROUP BY time_id, prod_subcategory, cust_city;
Oracle knows that those ranges of rows in the materialized view are fresh and can therefore rewrite the query with the materialized view. The rewritten query looks as follows:
SELECT time_id, prod_subcategory, cust_city, sum_amount_sold FROM sum_sales_per_city_mv WHERE time_id BETWEEN TO_DATE('01-JAN-2000', 'DD-MON-YYYY') AND TO_DATE('01-JUL-2000', 'DD-MON-YYYY');
Instead of the partitioning key, a partition marker (a function that identifies the partition given a rowid) can be present in the select (and GROUP BY list) of the materialized view. You can use the materialized view to rewrite queries that require data from only certain partitions (identifiable by the partition-marker), for instance, queries that reference a partition-extended table-name or queries that have a predicate specifying ranges of the partitioning keys containing entire partitions. See Chapter 8, "Materialized Views" for details regarding the supplied partition marker function DBMS_MVIEW.PMARKER.
The following example illustrates the use of a partition marker in the materialized view instead of the direct usage of the partition key column.
CREATE MATERIALIZED VIEW sum_sales_per_city_2_mv ENABLE QUERY REWRITE AS SELECT DBMS_MVIEW.PMARKER(s.rowid) AS pmarker, t.fiscal_quarter_desc, p.prod_subcategory, c.cust_city, SUM(s.amount_sold) AS sum_amount_sold FROM sales s, products p, customers c, times t WHERE s.cust_id = c.cust_id AND s.prod_id = p.prod_id AND s.time_id = t.time_id GROUP BY DBMS_MVIEW.PMARKER(s.rowid), prod_subcategory, cust_city, fiscal_quarter_desc;
Suppose you know that the partition sales_q1_2000 is fresh and DML changes have taken place for other partitions of the sales table. For testing purposes, you can apply an arbitrary DML operation on sales, changing a different partition than sales_q1_2000 when the materialized view is fresh. For example:
INSERT INTO SALES VALUES(10,10,'01-dec-2000','S',10,123.45,54321);
Although the materialized view sum_sales_per_city_2_mv is now considered generically stale, Oracle can rewrite the following query using this materialized view. This query restricts the data to the partition sales_q1_2000, and selects only certain values of cust_city, as shown in the following:
SELECT p.prod_subcategory, c.cust_city, SUM(s.amount_sold) AS sum_amount_sold FROM sales s, products p, customers c WHERE s.cust_id = c.cust_id AND s.prod_id = p.prod_id AND c.cust_city= 'Nuernberg' AND s.time_id >= TO_DATE('01-JAN-2000','dd-mon-yyyy') AND s.time_id < TO_DATE('01-APR-2000','dd-mon-yyyy') GROUP BY prod_subcategory, cust_city;
The same query could have been expressed with a partition-extended name as in the following statement:
SELECT p.prod_subcategory, c.cust_city, SUM(s.amount_sold) AS sum_amount_sold FROM sales partition (sales_q1_2000) s, products p, customers c WHERE s.cust_id = c.cust_id AND s.prod_id = p.prod_id AND c.cust_city= 'Nuernberg' GROUP BY prod_subcategory, cust_city;
Note that rewrite with a partially stale materialized view that contains a PMARKER function can only take place when the complete data content of one or more partitions is accessed and the predicate condition is on the partitioned fact table itself, as shown in the earlier example.
The DBMS_MVIEW.PMARKER function gives you exactly one distinct value for each partition. This dramatically reduces the number of rows in a potential materialized view compared to the partitioning key itself, but you are also giving up any detailed information about this key. The only thing you know is the partition number and, therefore, the lower and upper boundary values. This is the trade-off for reducing the cardinality of the range partitioning column and thus the number of rows.
Assuming the value of p_marker for partition sales_q1_2000 is 31070, the previously shown queries can be rewritten against the materialized view as:
SELECT mv.prod_subcategory, mv.cust_city, SUM(mv.sum_amount_sold) FROM sum_sales_per_city_2_mv mv WHERE mv.pmarker = 31070 AND mv.cust_city= 'Nuernberg' GROUP BY prod_subcategory, cust_city;
So the query can be rewritten against the materialized view without accessing stale data.
Complex materialized views are views that are not uniquely resolvable for query rewrite. Rewrite capability with complex materialized views is restricted to text match-based rewrite (partial or full). You can define a materialized view using arbitrarily complex SQL query expressions, but such a materialized view is treated as complex by query rewrite.
For example some of the constructs that make a materialized view complex are: set operators (UNION, UNION ALL, INTERSECT, MINUS), START WITH clause, CONNECT BY clause, and so on. Oracle currently supports general rewrite with inline views and self-joins on certain cases. These are the cases when the texts of inline view in the query and materialized view exactly match and the aliases of the duplicate tables in both the query and materialized view exactly match. All other cases involving inline views and self-joins will make a materialized view complex.
Query rewrite is attempted iteratively to take advantage of nested materialized views. Oracle first tries to rewrite a query with a materialized view having aggregates and joins, then with a materialized join view. If any of the rewrites succeeds, Oracle repeats that process again until no rewrites have occurred.
For example, assume that you had created a materialized views join_sales_time_product_mv and sum_sales_time_product_mv:
CREATE MATERIALIZED VIEW join_sales_time_product_mv ENABLE QUERY REWRITE AS SELECT p.prod_id, p.prod_name, t.time_id, t.week_ending_day, s.channel_id, s.promo_id, s.cust_id, s.amount_sold FROM sales s, products p, times t WHERE s.time_id=t.time_id AND s.prod_id = p.prod_id; CREATE MATERIALIZED VIEW sum_sales_time_product_mv ENABLE QUERY REWRITE AS SELECT mv.prod_name, mv.week_ending_day, COUNT(*) cnt_all, SUM(mv.amount_sold) sum_amount_sold, COUNT(mv.amount_sold) cnt_amount_sold FROM join_sales_time_product_mv mv GROUP BY mv.prod_name, mv.week_ending_day;
Consider the following query:
SELECT p.prod_name, t.week_ending_day, SUM(s.amount_sold) FROM sales s, products p, times t WHERE s.time_id=t.time_id AND s.prod_id=p.prod_id GROUP BY p.prod_name, t.week_ending_day;
Oracle first tries to rewrite it with a materialized aggregate view and finds there is none eligible (note that single-table aggregate materialized view sum_sales_store_time_mv cannot yet be used), and then tries a rewrite with a materialized join view and finds that join_sales_time_product_mv is eligible for rewrite. The rewritten query has this form:
SELECT mv.prod_name, mv.week_ending_day, SUM(mv.amount_sold) FROM join_sales_time_product_mv mv GROUP BY mv.prod_name, mv.week_ending_day;
Because a rewrite occurred, Oracle tries the process again. This time the query can be rewritten with single-table aggregate materialized view sum_sales_store_time into this form:
SELECT mv.prod_name, mv.week_ending_day, mv.sum_amount_sold FROM sum_sales_time_product_mv mv;
Oracle9i introduced extensions to the GROUP BY clause in the form of GROUPING SETS, ROLLUP, and their concatenation. These extensions enable you to selectively specify the groupings of interest in the GROUP BY clause of the query. For example, the following is a typical query with Grouping Sets:
SELECT p.prod_subcategory, t.calendar_month_desc, c.cust_city, SUM(s.amount_sold) AS sum_amount_sold FROM sales s, customers c, products p, times t WHERE s.time_id=t.time_id AND s.prod_id = p.prod_id AND s.cust_id = c.cust_id GROUP BY GROUPING SETS ( (p.prod_subcategory, t.calendar_month_desc), (c.cust_city, p.prod_subcategory) );
The term base grouping for queries with GROUP BY extensions denotes all unique expressions present in the GROUP BY clause. In the previous query, the following grouping (p.prod_subcategory, t.calendar_month_desc, c.cust_city,) is a base grouping.
The extensions can be present in user queries and in the queries defining materialized views. In both cases, materialized view rewrite applies and you can distinguish rewrite capabilities into the following scenarios:
When a query contains an extended GROUP BY clause, it can be rewritten with a materialized view if its base grouping can be rewritten using the materialized view as listed in the rewrite rules explained in "When Does Oracle Rewrite a Query?". For example, in the following query:
SELECT p.prod_subcategory, t.calendar_month_desc, c.cust_city, SUM(s.amount_sold) AS sum_amount_sold FROM sales s, customers c, products p, times t WHERE s.time_id=t.time_id AND s.prod_id = p.prod_id AND s.cust_id = c.cust_id GROUP BY GROUPING SETS ( (p.prod_subcategory, t.calendar_month_desc), (c.cust_city, p.prod_subcategory) );
The base grouping is: (p.prod_subcategory, t.calendar_month_desc, c.cust_city, p.prod_subcategory)) and, consequently, Oracle can rewrite the query using sum_sales_pscat_month_city_mv as follows:
SELECT mv.prod_subcategory, mv.calendar_month_desc, mv.cust_city, SUM(mv.sum_amount_sold) AS sum_amount_sold FROM sum_sales_pscat_month_city_mv mv GROUP BY GROUPING SETS ( (mv.prod_subcategory, mv.calendar_month_desc), (mv.cust_city, mv.prod_subcategory) );
A special situation arises if the query uses the EXPAND_GSET_TO_UNION hint. See "Hint for Queries with Extended GROUP BY" for an example of using EXPAND_GSET_TO_UNION.
In order for a materialized view with an extended GROUP BY to be used for rewrite, it must satisfy two additional conditions:
GROUPING_ID function on all GROUP BY expressions. For example, if the GROUP BY clause of the materialized view is GROUP BY CUBE(a, b), then the SELECT list should contain GROUPING_ID(a, b).GROUP BY clause of the materialized view should not result in any duplicate groupings. For example, GROUP BY GROUPING SETS ((a, b), (a, b)) would disqualify an materialized view from general rewrite.A materialized view with an extended GROUP BY contains multiple groupings. Oracle finds the grouping with the lowest cost from which the query can be computed and uses that for rewrite. For example, consider the materialized view:
CREATE MATERIALIZED VIEW sum_grouping_set_mv ENABLE QUERY REWRITE AS SELECT p.prod_category, p.prod_subcategory, c.cust_state_province, c.cust_city, GROUPING_ID(p.prod_category,p.prod_subcategory, c.cust_state_province,c.cust_city) AS gid, SUM(s.amount_sold) AS sum_amount_sold FROM sales s, products p, customers c WHERE s.prod_id = p.prod_id AND s.cust_id = c.cust_id GROUP BY GROUPING SETS ( (p.prod_category, p.prod_subcategory, c.cust_city), (p.prod_category, p.prod_subcategory, c.cust_state_province, c.cust_city), (p.prod_category, p.prod_subcategory) );
In this case, the following query:
SELECT p.prod_subcategory, c.cust_city, SUM(s.amount_sold) AS sum_amount_sold FROM sales s, products p, customers c WHERE s.prod_id = p.prod_id AND s.cust_id = c.cust_id GROUP BY p.prod_subcategory, c.cust_city;
This query will be rewritten with the closest matching grouping from the materialized view. That is, the (prodcategory, prod_subcategory, cust_city) grouping:
SELECT prod_subcategory, cust_city, SUM(sum_amount_sold) AS sum_amount_sold FROM sum_grouping_set_mv WHERE gid = grouping identifier of (prod_category,prod_subcategory, cust_city) GROUP BY prod_subcategory, cust_city;
When both materialized view and the query contain GROUP BY extensions, Oracle uses two strategies for rewrite: grouping match and UNION ALL rewrite. First, Oracle tries grouping match. The groupings in the query are matched against groupings in the materialized view and if all are matched with no rollup, Oracle selects them from the materialized view. For example, the following query:
SELECT p.prod_category, p.prod_subcategory, c.cust_state_province, c.cust_city, SUM(s.amount_sold) AS sum_amount_sold FROM sales s, products p, customers c WHERE s.prod_id = p.prod_id AND s.cust_id = c.cust_id GROUP BY GROUPING SETS ( (p.prod_category, p.prod_subcategory, c.cust_city), (p.prod_category, p.prod_subcategory) );
This query matches two groupings from sum_grouping_set_mv and Oracle rewrites the query as:
SELECT prod_subcategory, cust_city, sum_amount_sold FROM sum_grouping_set_mv WHERE gid = grouping identifier of (prod_category,prod_subcategory, cust_city) OR gid = grouping identifier of (prod_category,prod_subcategory)
In Oracle9i, release 2, if grouping match fails, Oracle tries a general rewrite mechanism called UNION ALL rewrite. Oracle first represents the query with the extended GROUP BY clause as an equivalent UNION ALL query. Every grouping of the original query is placed in a separate UNION ALL branch. The branch will have a simple GROUP BY clause. For example, consider this query:
SELECT p.prod_category, p.prod_subcategory, c.cust_state_province, t.calendar_month_desc, SUM(s.amount_sold) AS sum_amount_sold FROM sales s, products p, customers c WHERE s.prod_id = p.prod_id AND s.cust_id = c.cust_id GROUP BY GROUPING SETS ( (p.prod_subcategory, t.calendar_month_desc), (t.calendar_month_desc), (p.prod_category, p.prod_subcategory, c.cust_state_province), (p.prod_category, p.prod_subcategory) );
This is first represented as UNION ALL with four branches:
SELECT null, p.prod_subcategory, null, t.calendar_month_desc, SUM(s.amount_sold) AS sum_amount_sold FROM sales s, products p, customers c WHERE s.prod_id = p.prod_id AND s.cust_id = c.cust_id GROUP BY p.prod_subcategory, t.calendar_month_desc UNION ALL SELECT null, null, null, t.calendar_month_desc, SUM(s.amount_sold) AS sum_amount_sold FROM sales s, products p, customers c WHERE s.prod_id = p.prod_id AND s.cust_id = c.cust_id GROUP BY t.calendar_month_desc SELECT p.prod_category, p.prod_subcategory, c.cust_state_province, null, SUM(s.amount_sold) AS sum_amount_sold FROM sales s, products p, customers c WHERE s.prod_id = p.prod_id AND s.cust_id = c.cust_id GROUP BY p.prod_category, p.prod_subcategory, c.cust_state_province UNION ALL SELECT p.prod_category, p.prod_subcategory, null, null, SUM(s.amount_sold) AS sum_amount_sold FROM sales s, products p, customers c WHERE s.prod_id = p.prod_id AND s.cust_id = c.cust_id GROUP BY p.prod_category, p.prod_subcategory
Each branch is then rewritten separately using the rules from "When Does Oracle Rewrite a Query?". Using the materialized view sum_grouping_set_mv, Oracle can rewrite only branches 3 (which requires materialized view rollup) and 4 (which matches the materialized view exactly). The unrewritten branches will be converted back to the extended GROUP BY form. Thus, eventually, the query is rewritten as:
SELECT null, p.prod_subcategory, null, t.calendar_month_desc, SUM(s.amount_sold) AS sum_amount_sold FROM sales s, products p, customers c WHERE s.prod_id = p.prod_id AND s.cust_id = c.cust_id GROUP BY GROUPING SETS ( (p.prod_subcategory, t.calendar_month_desc), (t.calendar_month_desc), ) UNION ALL SELECT prod_category, prod_subcategory, cust_state_province, null, SUM(sum_amount_sold) AS sum_amount_sold FROM sum_grouping_set_mv WHERE gid = <grouping id of (prod_category,prod_subcategory, cust_city)> GROUP BY p.prod_category, p.prod_subcategory, c.cust_state_province UNION ALL SELECT prod_category, prod_subcategory, null, null, sum_amount_sold FROM sum_grouping_set_mv WHERE gid = <grouping id of (prod_category,prod_subcategory)>
Observe the following features of UNION ALL rewrite. First, a query with extended GROUP BY is represented as an equivalent UNION ALL and recursively submitted for rewrite optimization. The groupings that cannot be rewritten stay in the last branch of UNION ALL and access the base data instead.
Oracle9i introduced a new hint, the EXPAND_GSET_TO_UNION hint, to force expansion of the query with GROUP BY extensions into the equivalent UNION ALL query. This hint can be in an environment where materialized views have simple GROUP BY clauses only. In this case, we extend rewrite flexibility as each branch can be independently rewritten by a separate materialized view.
| See Also:
Oracle9i Database Performance Tuning Guide and Reference for more information regarding |
Because query rewrite occurs transparently, special steps have to be taken to verify that a query has been rewritten. Of course, if the query runs faster, this should indicate that rewrite has occurred, but that is not proof. Therefore, to confirm that query rewrite does occur, use the EXPLAIN PLAN statement or the DBMS_MVIEW.EXPLAIN_REWRITE procedure.
The EXPLAIN PLAN facility is used as described in Oracle9i SQL Reference. For query rewrite, all you need to check is that the object_name column in PLAN_TABLE contains the materialized view name. If it does, then query rewrite will occur when this query is executed.
In this example, the materialized view cal_month_sales_mv has been created.
CREATE MATERIALIZED VIEW cal_month_sales_mv ENABLE QUERY REWRITE AS SELECT t.calendar_month_desc, SUM(s.amount_sold) AS dollars FROM sales s, times t WHERE s.time_id = t.time_id GROUP BY t.calendar_month_desc;
If EXPLAIN PLAN is used on the following SQL statement, the results are placed in the default table PLAN_TABLE. However, PLAN_TABLE must first be created using the utlxplan.sql script.
EXPLAIN PLAN FOR SELECT t.calendar_month_desc, SUM(s.amount_sold) FROM sales s, times t WHERE s.time_id = t.time_id GROUP BY t.calendar_month_desc;
For the purposes of query rewrite, the only information of interest from PLAN_TABLE is the OBJECT_NAME, which identifies the objects that will be used to execute this query. Therefore, you would expect to see the object name calendar_month_sales_mv in the output as illustrated here.
SELECT object_name FROM plan_table; OBJECT_NAME ----------------------- CALENDAR_MONTH_SALES_MV 2 rows selected.
It can be difficult to understand why a query did not rewrite. The rules governing query rewrite eligibility are quite complex, involving various factors such as constraints, dimensions, query rewrite integrity modes, freshness of the materialized views, and the types of queries themselves. In addition, you may want to know why query rewrite chose a particular materialized view instead of another. To help with this matter, Oracle provides a PL/SQL procedure (DBMS_MVIEW.EXPLAIN_REWRITE) to advise you when a query can be rewritten and, if not, why not. Using the results from DBMS_MVIEW.EXPLAIN_REWRITE, you can take the appropriate action needed to make a query rewrite if at all possible.
You can obtain the output from DBMS_MVIEW.EXPLAIN_REWRITE in two ways. The first is to use a table, while the second is to create a varray. The following shows the basic syntax for using an output table:
DBMS_MVIEW.EXPLAIN_REWRITE ( query VARCHAR2(2000), mv VARCHAR2(30), statement_id VARCHAR2(30) );
You can create an output table named REWRITE_TABLE by executing the Oracle-supplied script utlxrw.sql.
The QUERY parameter is a text string representing the SQL query. The parameter, MV, is a fully qualified materialized view name in the form of SCHEMA.MV. This is an optional parameter. When it is not specified, EXPLAIN_REWRITE returns any relevant error messages regarding all the materialized views considered for rewriting the given query. When SCHEMA is omitted and only MV is specified, EXPLAIN_REWRITE looks for the materialized view in the current schema.
Therefore, to call the EXPLAIN_REWRITE procedure using an output table is as follows:
DBMS_MVIEW.EXPLAIN_REWRITE ( query VARCHAR2(2000), mv VARCHAR2(30), statement_id VARCHAR2(30) );
If you want to direct the output of EXPLAIN_REWRITE to a varray instead of a table, you should call the procedure as follows:
DBMS_MVIEW.EXPLAIN_REWRITE ( query VARCHAR2(2000), mv VARCHAR2(30), output_array SYS.RewriteArrayType );
Output of EXPLAIN_REWRITE can be directed to a table named REWRITE_TABLE. You can create this output table by running the Oracle-supplied script utlxrw.sql. This script can be found in the admin directory. The format of REWRITE_TABLE is as follows.
CREATE TABLE REWRITE_TABLE( statement_id VARCHAR2(30), -- ID for the query mv_owner VARCHAR2(30), -- MV's schema mv_name VARCHAR2(30), -- Name of the MV sequence INTEGER, -- Seq # of error msg query VARCHAR2(2000),-- user query message VARCHAR2(512), -- EXPLAIN_REWRITE error msg pass VARCHAR2(3), -- Query Rewrite pass no flags INTEGER, -- For future use reserved1 INTEGER, -- For future use reserved2 VARCHAR2(256); -- For future use );
An example PL/SQL invocation is:
EXECUTE DBMS_MVIEW.EXPLAIN_REWRITE \ ('SELECT p.prod_name, SUM(amount_sold) ' ||\ 'FROM sales s, products p ' ||\ 'WHERE s.prod_id = p.prod_id ' ||\ ' AND prod_name > ''B%'' ' ||\ ' AND prod_name < ''C%'' ' ||\ 'GROUP BY prod_name', \ 'TestXRW.PRODUCT_SALES_MV', \ 'SH'); SELECT message FROM rewrite_table ORDER BY sequence; MESSAGE -------------------------------------------------------------------------------- QSM-01033: query rewritten with materialized view, PRODUCT_SALES_MV 1 row selected.
Here is another example where you can see a more detailed explanation of why some materialized views were not considered and eventually the materialized view sales_mv was chosen as the best one.
DECLARE qrytext VARCHAR2(500) :='SELECT cust_first_name, cust_last_name, SUM(amount_sold) AS dollar_sales FROM sales s, customers c WHERE s.cust_id= c.cust_id GROUP BY cust_first_name, cust_last_name'; idno VARCHAR2(30) :='ID1'; BEGIN DBMS_MVIEW.EXPLAIN_REWRITE(querytxt, '', idno); END; / SELECT message FROM rewrite_table ORDER BY sequence;
SQL> MESSAGE -------------------------------------------------------------------------------- QSM-01082: Joining materialized view, CAL_MONTH_SALES_MV, with table, SALES, not possible QSM-01022: a more optimal materialized view than PRODUCT_SALES_MV was used to rewrite QSM-01022: a more optimal materialized view than FWEEK_PSCAT_SALES_MV was used to rewrite QSM-01033: query rewritten with materialized view, SALES_MV
You can save the output of EXPLAIN_REWRITE in a PL/SQL varray. The elements of this array are of the type RewriteMessage, which is defined in the SYS schema as shown in the following:
TYPE RewriteMessage IS record( mv_owner VARCHAR2(30), -- MV's schema mv_name VARCHAR2(30), -- Name of the MV sequence INTEGER, -- Seq # of error msg query VARCHAR2(2000),-- user query message VARCHAR2(512), -- EXPLAIN_REWRITE error msg pass VARCHAR2(3), -- Query Rewrite pass no flags INTEGER, -- For future use reserved1 INTEGER, -- For future use reserved2 VARCHAR2(256) -- For future use );
The array type, RewriteArrayType, which is a varray of RewriteMessage objects, is defined in SYS schema as follows:
TYPE RewriteArrayType AS VARRAY(256) OF RewriteMessage;
Using this array type, now you can declare an array variable and specify it in the EXPLAIN_REWRITE statement.
RewriteMessage record provides a message concerning rewrite processing.
The parameters are the same as for REWRITE_TABLE, except for statement_id, which is not used when using a varray as output.
mv_owner field defines the owner of materialized view that is relevant to the message.mv_name field defines the name of a materialized view that is relevant to the message.sequence field defines the sequence in which messages should be ordered.query field contains the first 2000 characters of the query text under analysis.message field contains the text of message relevant to rewrite processing of query.flags, reserved1, and reserved2 fields are reserved for future use.Consider the following query:
SELECT c.cust_state_province, AVG(s.amount_sold) FROM sales s, customers c WHERE s.cust_id = c.cust_id GROUP BY c.cust_state_province;
If that is used with the following materialized view:
CREATE MATERIALIZED VIEW avg_sales_city_state_mv ENABLE QUERY REWRITE AS SELECT c.cust_city, c.cust_state_province, AVG(s.amount_sold) FROM sales s, customers c WHERE s.cust_id = c.cust_id GROUP BY c.cust_city, c.cust_state_province;
The query will not rewrite with this materialized view. This can be quite confusing to a novice user as it seems like all information required for rewrite is present in the materialized view. The user can find out from DBMS_MVIEW.EXPLAIN_REWRITE that AVG cannot be computed from the given materialized view. The problem is that a ROLLUP is required here and AVG requires a COUNT or a SUM to do ROLLUP.
An example PL/SQL block for the previous query, using a varray as its output medium, is as follows:
SET SERVEROUTPUT ON DECLARE Rewrite_Array SYS.RewriteArrayType := SYS.RewriteArrayType(); querytxt VARCHAR2(1500) := 'SELECT S.CITY, AVG(F.DOLLAR_SALES) FROM STORE S, FACT F WHERE S.STORE_KEY = F.STORE_KEY GROUP BY S.CITY'; i NUMBER; BEGIN DBMS_MVIEW.Explain_Rewrite(querytxt, 'MV_CITY_STATE', Rewrite_Array); FOR i IN 1..Rewrite_Array.count LOOP DBMS_OUTPUT.PUT_LINE(Rewrite_Array(i).message); END LOOP; END; /
Following is the output of this EXPLAIN_REWRITE statement:
>> MV_NAME : MV_CITY_STATE >> QUERY : SELECT S.CITY, AVG(F.DOLLAR_SALES) FROM STORE S, FACT F WHERE S.ST ORE_KEY = F.STORE_KEY GROUP BY S.CITY >> MESSAGE : QSM-01065: materialized view, MV_CITY_STATE, cannot compute measure, AVG, in the query DBMS_MVIEW.Explain_Rewrite(querytxt, 'ID1', 'MV_CITY_STATE', user_name, Rewrite_Array);
The following design considerations will help in getting the maximum benefit from query rewrite. They are not mandatory for using query rewrite and rewrite is not guaranteed if you follow them. They are general rules of thumb.
Make sure all inner joins referred to in a materialized view have referential integrity (foreign key - primary key constraints) with additional NOT NULL constraints on the foreign key columns. Since constraints tend to impose a large overhead, you could make them NO VALIDATE and RELY and set the parameter QUERY_REWRITE_INTEGRITY to stale_tolerated or trusted. However, if you set QUERY_REWRITE_INTEGRITY to enforced, all constraints must be enforced to get maximum rewritability.
You can express the hierarchical relationships and functional dependencies in normalized or denormalized dimension tables using the HIERARCHY and DETERMINES clauses of a dimension. Dimensions can express intra-table relationships which cannot be expressed by any constraints. Set the parameter QUERY_REWRITE_INTEGRITY to trusted or stale_tolerated for query rewrite to take advantage of the relationships declared in dimensions.
Another way of avoiding constraints is to use outer joins in the materialized view. Query rewrite will be able to derive an inner join in the query, such as (A.a=B.b), from an outer join in the materialized view (A.a = B.b(+)), as long as the rowid of B or column B.b is available in the materialized view. Most of the support for rewrites with outer joins is provided for materialized views with joins only. To exploit it, a materialized view with outer joins should store the rowid or primary key of the inner table of an outer join. For example, the materialized view join_sales_time_product_mv_oj stores the primary keys prod_id and time_id of the inner tables of outer joins.
If you need to speed up an extremely complex, long-running query, you could create a materialized view with the exact text of the query. Then the materialized view would contain the query results, thus eliminating the time required to perform any complex joins and search through all the data for that which is required.
To get the maximum benefit from query rewrite, make sure that all aggregates which are needed to compute ones in the targeted set of queries are present in the materialized view. The conditions on aggregates are quite similar to those for incremental refresh. For instance, if AVG(x) is in the query, then you should store COUNT(x) and AVG(x) or store SUM(x) and COUNT(x) in the materialized view.
| See Also:
"General Restrictions on Fast Refresh" for requirements for fast refresh |
Aggregating data at lower levels in the hierarchy is better than aggregating at higher levels because lower levels can be used to rewrite more queries. Note, however, that doing so will also take up more space. For example, instead of grouping on state, group on city (unless space constraints prohibit it).
Instead of creating multiple materialized views with overlapping or hierarchically related GROUP BY columns, create a single materialized view with all those GROUP BY columns. For example, instead of using a materialized view that groups by city and another materialized view that groups by month, use a materialized view that groups by city and month.
Use GROUP BY on columns which correspond to levels in a dimension but not on columns that are functionally dependent, because query rewrite will be able to use the functional dependencies automatically based on the DETERMINES clause in a dimension. For example, instead of grouping on prod_name, group on prod_id (as long as there is a dimension which indicates that the attribute prod_id determines prod_name, you will enable the rewrite of a query involving prod_name).
If several queries share the same common subexpression, it is advantageous to create a materialized view with the common subexpression as one of its SELECT columns. This way, the performance benefit due to precomputation of the common subexpression can be obtained across several queries.
When creating a materialized view which aggregates data by folded date granules such as months or quarters or years, always use the year component as the prefix but not as the suffix. For example, TO_CHAR(date_col, 'yyyy-q') folds the date into quarters, which collate in year order, whereas TO_CHAR(date_col, 'q-yyyy') folds the date into quarters, which collate in quarter order. The former preserves the ordering while the latter does not. For this reason, any materialized view created without a year prefix will not be eligible for date folding rewrite.
Optimization with materialized views is based on cost and the optimizer needs statistics of both the materialized view and the tables in the query to make a cost-based choice. Materialized views should thus have statistics collected using the DBMS_STATS package.
|
 Copyright © 1996, 2002 Oracle Corporation. All Rights Reserved. |
|