11 Modifying Default Security Behavior of Oracle Composer Components
You can override the default security definitions at various levels in keeping with your business requirement. For information about the default security behavior of Oracle Composer components, see Section 5.7, "Security and Oracle Composer."
This chapter describes how to override the default security behavior of Oracle Composer components. It contains the following subsections:
-
Section 11.1, "Applying Component-Level Restrictions by Defining Customization Policies"
-
Section 11.3, "Applying Tag-Level Security Using the customizationAllowed Attribute"
11.1 Applying Component-Level Restrictions by Defining Customization Policies
By default, the MDS restricts customization of page components, that is, users cannot customize components or their attributes at runtime. To enable customization, you must lift the default restrictions on components and their attributes. When you add a Page Customizable component to the page and populate it with content, the default customization restrictions on the Page Customizable and all its child components are lifted. However, in some instances, such as when the Page Customizable component is part of the template used for the page, you may need to explicitly allow customization of components and their attributes. This section describes how to apply MDS type-level restrictions or instance-level restrictions on components and their attributes. It contains the following subsections:
-
Section 11.1.1, "How to Define Type-Level Customization Policies"
-
Section 11.1.2, "How to Define Instance-Level Customization Policies"
Note:
For information about creating customizable pages using page templates, see Section 7.1.7, "How to Create a Page Template for Creating Customizable Pages."11.1.1 How to Define Type-Level Customization Policies
When you apply type-level restrictions on a component, all instances of the component are restricted. This is useful if you want to allow only a specific set of users to edit a particular component or its attributes while restricting all other users from editing it. For example, if you want to allow only a page creator or application administrator to change the page layout at runtime, you can define type-level restrictions on the Layout Customizable component and enable only users with admin role to edit this component.
You can enable type-level restrictions on components and their attributes in a standalone XML file and then register this file in the mds-config section of the adf-config.xml file or in an mds-config.xml file. The standalone XML file contains annotations that match the types for which customization restrictions must be specified.
You can create an mds-config.xml file in your application's META-INF directory and register the standalone file in the mds-config.xml file.
To enable customization of selected components or attributes at the type level:
-
Create an XML document, for example
standalone.xml, add the following code, and replace the text in bold with appropriate values:<?xml version="1.0" encoding="UTF-8" ?> <grammarMetadata xmlns="http://xmlns.oracle.com/bali/xml/metadata" xmlns:mds="http://xmlns.oracle.com/mds" namespace="tag_namespace"> <elementMetadata elementName="component_name"> <mds:customizationAllowed>true</mds:customizationAllowed> <attributeMetadata attributeName="attribute_name"> <mds:customizationAllowedBy>security_roles</mds:customizationAllowedBy> </attributeMetadata> </elementMetadata> </grammarMetadata>The
<customizationAllowedBy>tag can appear only once. Multiple values can be specified as a space-separated list of allowed policies as part of the declaration. To enable or disable customization for specific users or roles, the users or roles must be included in the customization policy of the MDS session. For more information, see Section 11.2.3, "How to Customize the SessionOptions Object to Include Customization Policy."The
<customizationAllowed>tag takes a Boolean as its value. A value oftruefor this tag means that anyone can customize the specified component, so long as other inherited customization polices allow it.The
<customizationAllowedBy>tags do not serve any purpose if the same object has been tagged with<customizationAllowed>false</ customizationAllowed>. Additionally, the customization must be allowed at the top level of the object tree. Otherwise the default behavior dictates that no customization can be permitted at a lower level. -
Register this XML file in either of the following ways:
To register the XML file in the
adf-config.xmlfile, add thetype-configelement inside themds-configsection using the following format:<mds-config xmlns="http://xmlns.oracle.com/mds/config"> <type-config> <standalone-definitions> <classpath>File_Path/standalone.xml</classpath> </standalone-definitions> </type-config> </mds-config>Create an
mds-config.xmlfile in your application'sMETA-INFfolder and add atype-configelement inside themds-component-configsection of the file in the following format:<?xml version="1.0" encoding="UTF-8" ?> <mds-component-config version="11.1.1.000" xmlns="http://xmlns.oracle.com/mds/config"> <type-config> <standalone-definitions> <classpath>File_Path/standalone.xml</classpath> </standalone-definitions> </type-config> </mds-component-config> -
Make the standalone files and associated XSDs available in a shared library JAR file; otherwise MDS cannot load them.
At runtime, MDS searches all
mds-configinstances in theMETA-INFdirectories and loads all the customization restrictions specified in standalone files.
11.1.2 How to Define Instance-Level Customization Policies
Instance-level restrictions are useful if you want to allow or restrict customization of a particular instance of a component. The code for instance-level customization policies is similar to that used in the type-level policy definitions. However, instance level policies override type-level policies. That is, instance-level restrictions hold true irrespective of the restrictions from the type. For example, if you have used a form with some UI elements in your login page and in other pages such as a user preferences page, you may want to allow users to customize all instances of the form except on the login page. For this, you can allow customization of the form at the type level and restrict customization only on the instance in the login page.
You can enable customization on a component or any of its attributes at the instance level. To apply customization restriction at the component level, you can set the customizationAllowed and customizationAllowedBy attributes on the component in JDeveloper (see Section 11.1.1, "How to Define Type-Level Customization Policies"). To apply restrictions on a component's attributes, perform the steps described in this section.
Instance-level policies for component attributes are defined in an RDF file. The RDF file is picked up by MDS, and the policies are implemented.
To define instance-level customization policies:
-
Create an RDF file with the same name as the JSPX file, but using the RDF extension, for example
main.jspx.rdf.Create this file in the
application_home/project/public_html/mdssys/mdxfolder. Creating the RDF file in this folder structure ensures that the file is picked up by MDS and the policies defined here are implemented. -
Include tags in the following format to apply restrictions on a component's attribute:
tag_id(xmlns(tag_prefix=tag_namespace))/@tag_prefix:attribute_name
The following example shows how to apply a restriction on a
Go Image Linkcomponent and thetextattribute of aCommand Buttoncomponent:<?xml version="1.0" encoding="UTF-8"?> <rdf:RDF xmlns:rdf="http://www.w3.org/1999/02/22-rdf-syntax-ns#" xmlns:dc="http://purl.org/dc/elements/1.1/"> <rdf:Description rdf:about="/"/> <!-- Opens the customization on a tag, for example, an af:goImageLink whose ID is 'gil1'. --> <rdf:Description rdf:about="gil1"> <customizationAllowed xmlns="http://xmlns.oracle.com/mds">false</customizationAllowed> </rdf:Description> <!-- Restricts customizations on a commandButton component's 'text' attribute. --> <rdf:Description rdf:about="cb1(xmlns(af=http://xmlns.oracle.com/adf/faces/rich))/@af:text"> <customizationAllowed xmlns="http://xmlns.oracle.com/mds">false</customizationAllowed> </rdf:Description>
At runtime, these policies are read and the artifacts are enabled for customization accordingly.
11.2 Applying a Component Instance-Level Customization Restriction By Using Security Roles: Example
This section explains how you can use component-level restrictions to limit access to certain component functions, based on different user roles and responsibilities. Specifically, it describes how to apply an instance-level customization restriction to a Panel Customizable component to provide customization access to only users with admin role. That is, when a user with admin role logs into the system at runtime, the user can customize the Panel Customizable on which the instance-level customization is applied.
In Oracle Composer's Property Inspector, the properties of the Panel Customizable are not displayed to users who do not have admin privileges. The Edit icon or menu item is disabled on restricted components. These users cannot drop any Movable Box into the Panel Customizable because of the applied restriction. Moreover, they cannot rearrange the Show Detail Frames inside this Panel Customizable.
To restrict a functionality based on user roles is one way to apply customization restrictions. You can also use expression language expressions (ELs), which provide roles-based results, to enable or restrict access to a component function.
Note:
MDS customization restrictions are natively honored only byPanel Customizable, Show Detail Frame, and Layout Customizable components, and not ADF Faces components, such as Splitter and showDetailItem.This section contains the following subsections:
-
Section 11.2.2, "How to Define Roles and Grant Privileges in the jazn-data.xml File"
-
Section 11.2.3, "How to Customize the SessionOptions Object to Include Customization Policy"
-
Section 11.2.4, "How to Register the Implementation with Oracle Composer"
-
Section 11.2.6, "How to Apply an Instance-Level Customization Restriction"
11.2.1 How to Configure ADF Security
Before applying an instance-level customization restriction, you must secure your application using ADF security. For information, see Section 3.5.1, "How to Configure ADF Security."
11.2.2 How to Define Roles and Grant Privileges in the jazn-data.xml File
In a previous section, a customization restriction is applied to a Panel Customizable component so that, at runtime, only the user with admin role can access all the features of Panel Customizable, and therefore, can customize its attributes.
In this section, two roles, admin and customer, are created and page permissions are granted to both users. Users with admin role can customize the Panel Customizable (panelCustomizable1) component. However, because of the customization restriction you applied in an earlier section, users with customer role do not have the rights to customize panelCustomizable1, and these users cannot use all the features of panelCustomizable1.
To create roles in the jazn-data.xml file:
-
In the Application Resources panel, right-click the jazn-data.xml file and select Open.
-
Click the Users and Roles tab at the bottom of the editor to open the Users section of the file, shown in Figure 11-1.
-
Click the Application Roles tab.
-
In the Application Roles page, click the New Application Role icon in the Roles table, shown in Figure 11-2.
Figure 11-2 Roles Section in the jazn-data.xml File

Description of "Figure 11-2 Roles Section in the jazn-data.xml File"
-
In the Name field, specify the user name,
admin. -
Optionally, in the Display Name and Description fields, specify a display name and description for the new role.
-
Repeat steps 3 through 6 to add another role,
customer. -
Click the Users tab.
-
In the Users page, create new users by clicking the New User icon and specifying credentials, and assign roles to these users by clicking the Assign Roles icon in the Assigned Roles table and selecting Assign Application Role, as shown in Figure 11-3.
Figure 11-3 Users Section in the jazn-data.xml File

Description of "Figure 11-3 Users Section in the jazn-data.xml File"
-
Click the ADF Policies tab at the bottom of the page.
-
Select the Web Pages tab on the page.
-
From the list of page definitions, select the page on which you want to grant privileges, as shown in Figure 11-4.
Figure 11-4 Page Definitions in the jazn-data.xml File

Description of "Figure 11-4 Page Definitions in the jazn-data.xml File"
-
In the Granted to Roles column, click the Add Application Role icon.
-
In the Select Roles dialog (Figure 11-5), select the
adminandcustomerroles and click OK. -
Select each role and grant all the permissions (View, Customize, Edit, Grant, Personalize), as shown in Figure 11-6.
Figure 11-6 Permissions List in the jazn-data.xml File
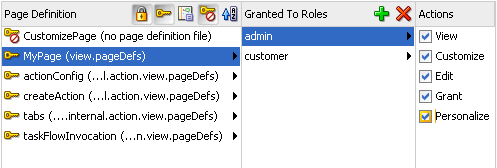
Description of "Figure 11-6 Permissions List in the jazn-data.xml File"
For more information about creating users and roles, see the section "Enabling ADF Security in a Fusion Web Application" in the Oracle Fusion Middleware Fusion Developer's Guide for Oracle Application Development Framework.
11.2.3 How to Customize the SessionOptions Object to Include Customization Policy
To enable the expected runtime behavior of the Panel Customizable component, where only the user with admin role has access to all capabilities of the Panel Customizable, including the ability to customize it, the MDS session for this request must include the user roles in its customization policy. To achieve this, the following customization policy is included in the SessionOptions object:
SecurityContext stx = ADFContext.getCurrent().getSecurityContext(); cPol = new CustomizationPolicy(stx.getUserRoles());
Then the MDS session is created with this customization policy.
To implement the ComposerSessionOptionsFactory class:
-
From the File menu, choose New.
-
In the New Gallery dialog, expand General, select Java, then Java Class, and click OK.
The Create Java Class dialog opens.
-
In the Name field, enter
AppsSessionOptionsFactoryImpl. -
Click OK.
The
AppsSessionOptionsFactoryImpl.javafile is rendered in the Source view. -
Import the following libraries:
import oracle.adf.share.ADFContext; import oracle.adf.share.security.SecurityContext; import oracle.adf.view.page.editor.mds.ComposerSessionOptionsFactory; import oracle.adf.view.page.editor.mode.ModeContext; import oracle.mds.config.CustClassListMapping; import oracle.mds.config.CustConfig; import oracle.mds.core.SessionOptions; import oracle.mds.cust.CustClassList; import oracle.mds.cust.CustomizationClass; import oracle.mds.cust.CustomizationPolicy;
-
Add the following code to implement the
ComposerSessionOptionsFactoryclass and provideSessionOptions:public class AppsSessionOptionsFactoryImpl implements ComposerSessionOptionsFactory { public AppsSessionOptionsFactoryImpl() { } public SessionOptions createSessionOptions(SessionOptions sessionOptions, String mode) { CustomizationClass[] custLayer; CustConfig custConfig = null; CustomizationPolicy cPol = null; if (ModeContext.EDIT_MODE.equals(mode)) { //Mode is Edit, change to SiteCC custLayer = EDIT_LAYER; } else { //Mode is View, change to UserCC + SiteCC custLayer = VIEW_LAYER; } try { CustClassList custClassList = new CustClassList(custLayer); CustClassListMapping custClassListMapping = new CustClassListMapping("/", null, null, custClassList); custConfig = new CustConfig(new CustClassListMapping[] { custClassListMapping }); SecurityContext stx = ADFContext.getCurrent().getSecurityContext(); cPol = new CustomizationPolicy(stx.getUserRoles()); } catch (Exception e) { e.printStackTrace(); } if(sessionOptions.getServletContextAsObject() != null) { return new SessionOptions(sessionOptions.getIsolationLevel(), sessionOptions.getLocale(), custConfig, sessionOptions.getVersionContext(), sessionOptions.getVersionCreatorName(), cPol == null ? sessionOptions.getCustomizationPolicy() : cPol, sessionOptions.getServletContextAsObject()); } else { return new SessionOptions(sessionOptions.getIsolationLevel(), sessionOptions.getLocale(), custConfig, sessionOptions.getVersionContext(), sessionOptions.getVersionCreatorName(), cPol == null ? sessionOptions.getCustomizationPolicy() : cPol); } } //Edit mode SiteCC private static final CustomizationClass[] EDIT_LAYER = new CustomizationClass[] { new SiteCC() }; //View mode SiteCC + USerCC private static final CustomizationClass[] VIEW_LAYER = new CustomizationClass[] { new SiteCC(), new UserCC() }; }
11.2.4 How to Register the Implementation with Oracle Composer
Perform the steps described in Section 10.3.5, "How to Register the Implementation with Oracle Composer" to register the ComposerSessionOptionsFactory class implementation, where user roles were included in the MDS session's customization policy.
11.2.5 How to Configure WebCenterComposerFilter
To configure WebCenterComposerFilter, perform the steps described in Section 10.3.6, "How to Configure WebCenterComposerFilter."
11.2.6 How to Apply an Instance-Level Customization Restriction
In this section, you enable customization for particular role on a Panel Customizable component. At runtime, only the specified role, for example admin, can access all the features of the Panel Customizable, including customizing its attributes. Users with any other roles can use only a limited set of component features.
To apply an instance-level customization restriction:
-
In the JSPX page, add a Change Mode Link component from the Oracle Composer tag library.
-
Add a Page Customizable component below the
Change Mode Linkcomponent. -
Apply an instance-level customization restriction on the component
Panel Customizablein the Page Customizable.This restriction is stored in the following directory:
public_html/mdssys/mdx/<pagename>.jspx.rdf.The Source view should look like this:
<pe:changeModeLink id="cml1"/> <pe:pageCustomizable id="pageCustomizable1"> <cust:panelCustomizable id="panelCustomizable1" layout="scroll"/> <f:facet name="editor"> <pe:pageEditorPanel id="pep1"/> </f:facet> </pe:pageCustomizable>The design view should look like Figure 11-7.
Figure 11-7 Design View: Customization Allowed

Description of "Figure 11-7 Design View: Customization Allowed"
-
Add a
Show Detail Framecomponent within thePanel Customizableand include anotherPanel Customizablecomponent as a child of theShow Detail Framecomponent.
Note:
This step is for illustration purpose only as it is easier to explain runtime behavior by showing multiple components. For detailed information on how to add Oracle Composer components, see Section 3.3.2, "How to Create a Page in a Manually-Created WebCenter Application."11.2.7 What Happens at Runtime
What happens at runtime is influenced by which user is logged on. To see the difference, log in as one user and then the other. For example:
In the Application Navigator, right-click the JSPX page and select Run.
Log in to the page as a user with admin role, and switch to Edit mode. The Add Content button and the Edit icon are displayed on the outer and inner Panel Customizable components. As a user with admin role, you can switch to Source view and access the properties of the outer Panel Customizable, as shown in Figure 11-8. That is, users with admin role can edit this component.
Log in to the page as a user with customer role, and switch to Edit mode. The Add Content button and the Edit icon are not available on the outer Panel Customizable. That is, this component is not editable for users with customer role. In Source view, the Add Content and Edit icons are grayed out for the component, as shown in Figure 11-9.
Figure 11-9 Restricted Component in Page Source View

Description of "Figure 11-9 Restricted Component in Page Source View"
11.3 Applying Tag-Level Security Using the customizationAllowed Attribute
By default, a Page Customizable component enables customization on all components under it. You may want to change this to restrict customization on some components. The Page Customizable component does not enable customization on components that are on a nested page or fragment. You must enable customization on such components manually. To address such requirements, MDS provides the customizationAllowed and customizationAllowedBy attributes. These attributes can be used to enable or restrict customization on specific component instances on a page.
The customizationAllowed attribute controls whether the component can be customized at runtime. If you set this attribute to false, then the component cannot be customized at runtime. That is, in the Component Properties dialog the properties are grayed out and do not allow editing.
The customizationAllowedBy attribute specifies the roles for which customization is enabled.
This section provides examples of enabling and restricting customization on a component. It contains the following subsections:
-
Section 11.3.1, "How to Enable Customization on an Image Component"
-
Section 11.3.2, "How to Restrict Customization on an Image Component"
For more information, see Extended Metadata and Annotation Properties in Oracle Fusion Middleware Fusion Developer's Guide for Oracle Application Development Framework.
11.3.1 How to Enable Customization on an Image Component
To enable customization on an Image component:
-
In the
MyPage.jspxpage that you created in Section 7.2, "Designing Editable Pages Using Oracle Composer Components: Example," add an ADF Faces Image component, for example,brandingImage.gif, inside thePanel CustomizablecalledpanelCustomizable1.Customization is enabled automatically on the
Imagecomponent since it is nested inside aPage Customizablecomponent. -
Run
MyPage.jspx. -
Switch to Edit mode of the page.
-
From the View menu, select Source to switch to Source view of the page.
-
Select the image in the component hierarchy in the Source View panel and click the Show the properties of Image icon.
The Component Properties dialog displays the image properties. You can edit any available property in this dialog. Edit a property and click OK. The property's editable value demonstrates that customization is enabled on the component.
11.3.2 How to Restrict Customization on an Image Component
You can restrict customization of an image on the page by setting the customizationAllowed attribute to false on the image component.
To restrict customization on the Image Component:
-
In Oracle JDeveloper, select the
Imagecomponent that you added in the previous section, and in the Property Inspector set the value for customizationAllowed tofalse. -
Run
MyPage.jspx. -
Switch to page Edit mode.
-
From the View menu, select Source to switch to the Source view of the page.
-
Select the image in the component hierarchy in the Source View panel, and click the Show the properties of Image icon.
In the Component Properties dialog, the properties are grayed out and cannot be edited.
11.4 Applying Attribute-Level Security
You can choose whether specific component attributes can be customized at runtime. Additionally, you can specify whether the changes made to an attribute must be persisted to a persistence store, such as MDS. You can apply attribute-level security in the following ways:
-
By defining property filters
-
By persisting changes at the component level
For information about applying property filters, see Section 8.7.1, "How to Define Property Filters."
This section describes how to persist changes at the component level. It contains the following subsections:
11.4.1 How to Define Change Persistence at the Component Level
If your application is configured to use FilteredPersistenceChangeManager to persist changes, you can use the persist-changes attribute in the adf-config.xml file to specify whether changes to a specific attribute must be persisted.
Note:
For information about change persistence, see Section 9.10, "Configuring the Persistence Change Manager."For information about the Oracle Composer-specific configurations you can make in adf-config.xml, see Section B.2.2, "adf-config.xml."
Example 11-1 shows a sample adf-config.xml file with persist-changes attributes defined for some attributes.
Example 11-1 Using the persist-changes Attribute in the adf-config.xml File
<adf-config xmlns="http://xmlns.oracle.com/adf/config">
<adf-faces-config xmlns="http://xmlns.oracle.com/adf/faces/config">
<persistent-change-manager>
<persistent-change-manager-class>
oracle.adf.view.rich.change.MDSDocumentChangeManager
</persistent-change-manager-class>
</persistent-change-manager>
<taglib-config>
<taglib uri="http://xmlns.oracle.com/adf/pageeditor">
<tag name="imageLink">
<attribute name="destination">
<persist-changes>true</persist-changes>
</attribute>
</tag>
<tag name="customAction">
<attribute name="text">
<persist-changes>true</persist-changes>
</attribute>
<attribute name="icon">
<persist-changes>true</persist-changes>
</attribute>
</tag>
</taglib>
</taglib-config>
</adf-faces-config>
</adf-config>
11.4.2 What Happens at Runtime
If you set persist-changes to true, then a change made to the component attribute is persisted in any instance of that component. If you set persist-changes to false, then even if you change the attribute value in the Component Properties dialog at runtime, the change is not saved.
11.5 Applying Action-Level Restrictions on Panel Customizable and Show Detail Component Actions
The ability of a user to perform actions on Panel Customizable and Show Detail Frame components is inherited from page security. Inheritance is based on the value of the application-wide switch, enableSecurity, in the adf-config.xml file. If you select the WebCenter Application template when you create your application, then the adf-config.xml file is located in the ADF META-INF folder under Descriptors in the Application Resources panel.
This section describes how to apply action-level restrictions on Panel Customizable and Show Detail Frame component actions. It contains the following subsections:
-
Section 11.5.1, "How to Add an enableSecurity Section to adf-config.xml"
-
Section 11.5.2, "Defining Security at the Actions Category Level"
11.5.1 How to Add an enableSecurity Section to adf-config.xml
The enableSecurity element is not available by default in adf-config.xml. To override or extend the page-level security inheritance for Panel Customizable and Show Detail Frame components, you must add the customizableComponentsSecurity section in the adf-config.xml file, as shown in Example 11-2, and set the enableSecurity element in that section to true.
Example 11-2 enableSecurity Element in the Customizable Components Security Section in adf-config.xml
<cust:customizableComponentsSecurity xmlns="http://xmlns.oracle.com/adf/faces/customizable/config"> <cust:enableSecurity value="true"/> <cust:actionsCategory> .......................................... </cust:customizableComponentsSecurity>
Restrictions on actions can be implemented at the following levels:
-
Page level: You can define security for WebCenter Customizable Components so that page-level privileges are inherited by these components. This is the default behavior.
By default, customizable components inherit allowable actions from the defined page-level permissions, such as edit, personalize, or customize. That is, a user who has edit, personalize, or customize privileges on a page can perform View mode personalizations on that page. The
enableSecurityelement enables you to override the security inheritance behavior. It can take either of the following values:-
true: If set totrue(the default when not specified), then the ability of a user to modify a component is first determined from the page permissions and then adjusted according to the current set of actions defined for that type of permission. For example, if a user has customize permission, then the actions that constitute the customize category (move, customize, and so on) are available to the user, but they are overridden by the actions that are defined in theadf-config.xmlfile. -
false: If set tofalse, then all actions are available to users. A user's page permissions and actions configured inadf-config.xmlare ignored.
-
-
Actions category level: You can define security on all actions for
Panel CustomizableandShow Detail Framecomponents.You can add an
actionsCategoryelement in theadf-config.xmlfile to define security on multiple actions simultaneously. Depending on theactionCategoryattributes that you enable, appropriate privileges are provided on the components. -
Actions level: You can define security on individual actions for
Panel CustomizableandShow Detail Framecomponents.You can use the
actionselement in theadf-config.xmlfile to enable or disable individual actions. Depending on theactionsattributes that you enable, appropriate privileges are provided on the components.
Notes:
-
If you set
enableSecuritytotruein theadf-config.xmlfile and define restrictions on actions or action categories, then for these restrictions to take effect you must grant Personalize or Customize privilege on the page, in addition to View privilege.If you are not using the
enableSecurityelement or it is set tofalse, then page-level permissions are honored. In such a case, having View privilege on the page is sufficient as all customizable components actions are rendered by default on the page. -
Privileges can be inherited from the parent only. Inheritance from a component in any other position in the hierarchy is not supported.
-
Restrictions defined at the actions category level or actions level are applicable to all instances of the
Panel CustomizableorShow Detail Framecomponent across the application. You cannot apply restrictions on a single instance of the component.
You can define security for component actions at the application level if enableSecurity is set to true in the adf-config.xml file. A value of true implies that permission checks are made in addition to the actionsCategory and actions values specified in the adf-config.xml.
11.5.2 Defining Security at the Actions Category Level
You can add an actionsCategory element in the customizable components actions security section in the adf-config.xml file to define security on multiple Panel Customizable and Show Detail Frame components actions. Depending on the actionsCategory attributes that you enable, appropriate privileges are provided on the components.
The actions and actionsCategory elements in the adf-config.xml file have certain default mappings. Table 11-1 describes the different actionsCategory attributes and the actions they support by default.
For information about the Oracle Composer-specific configurations you can make in adf-config.xml, see Section B.2.2, "adf-config.xml."
Table 11-1 Actions Categories and Show Detail Frame Actions Mapping
| actionsCategory | Actions Supported |
|---|---|
|
|
showMoveAction showRemoveAction showMinimizeAction showResizer allowAction |
|
|
showEditAction showAddContentAction showSplitAction |
The behavior of components based on a combination of personalizeActionsCategory and customizeActionsCategory settings is as follows:
-
If both
personalizeActionsCategoryandcustomizeActionsCategoryare set tofalse, then users cannot move, expand, collapse, delete, resize, or editShow Detail Framecomponents and they also cannot edit or deletePanel Customizablecomponents or add content inside them. -
If
personalizeActionsCategoryis set totrueandcustomizeActionsCategoryis set tofalse, then users can move, expand, collapse, delete, or resizeShow Detail Framecomponents but not edit them. Additionally, they can deletePanel Customizablecomponents and rearrange components inside them but not edit them or add components to the page.Note:
TheallowActionsetting, along with other actions settings, controls the ability to add content to the page and move or rearrange content on the page. For more information, see Section 11.5.3, "Defining Security at the Actions Level." -
If both
personalizeActionsCategoryandcustomizeActionsCategoryare set totrue, then users can move, expand, collapse, delete, resize, and editShow Detail Framecomponents and they can also edit and deletePanel Customizablecomponents and add content inside them. Users can add content from the Resource Catalog using the Add Content button, add Box components using the Add Box icons, and move components from otherPanel Customizablecomponents by dragging and dropping them.
Note:
It is not recommended that you setpersonalizeActionsCategory to false and customizeActionsCategory to true as privileges cascade from Grant to Customize to Personalize to View. That is, when you enable customization, the user must already have personalize privilege on the page.Example 11-3 shows the actionsCategory entry that you can add to the customizable components actions security section in the adf-config.xml file.
Example 11-3 actionsCategory Element in the Customizable Components Security Section
<cust:customizableComponentsSecurity
xmlns="http://xmlns.oracle.com/adf/faces/customizable/config">
<cust:enableSecurity value="true"/>
<cust:actionsCategory>
<cust:actionCategory name="personalizeActionsCategory" value="true"/>
<cust:actionCategory name="customizeActionsCategory" value="false"/>
</cust:actionsCategory>
<cust:actions>
..........................................
</cust:actions>
</cust:customizableComponentsSecurity>
You can also use EL for these element values, as shown in Example 11-4.
Example 11-4 EL Used in Customizable Components an actionCategory Entry
<cust:actionsCategory>
<cust:actionCategory name="personalizeActionsCategory" value="#{appBusinessRules.InsideCorpNetwork}"/>
</cust:actionsCategory>
For reference, the managed bean, appBusinessRules, is defined as shown in Example 37-7 in Section 37.10, "Overriding Inherited Security on Portlets and Customizable Components."
11.5.3 Defining Security at the Actions Level
You can use the actions element in the customizable components actions security section of the adf-config.xml file to enable or disable individual Show Detail Frame actions. Depending on the actions attributes that you enable, appropriate privileges are provided on the Show Detail Frame components.
For information about Oracle Composer-specific configurations you can make in adf-config.xml, see Section B.2.2, "adf-config.xml."
The allowAction setting, along with other actions settings, controls the ability add content to the page and move or rearrange page content.
In Oracle Composer, users can add and arrange content in the following ways:
-
Add
Boxcomponents using the Add Box icons. -
Add content inside a
Boxcomponent, from the Resource Catalog, using the Add Content button. -
Move
Show Detail Framecomponents within aPanel Customizablecomponent by using the Move Up and Move Down actions on theShow Detail Framecomponent's Actions menu. -
Drag and drop
Show Detail Framecomponents acrossPanel Customizablecomponents.
Table 11-2 explains the ability to add content depending on the allowAction and showAddContentAction settings.
Table 11-2 Actions Settings for Adding Content to a Page
| allowAction Setting | showAddContentAction Setting | Add Content Button Enabled? |
|---|---|---|
|
|
|
Yes |
|
|
|
No |
|
|
true |
No |
|
|
|
No |
Table 11-3 explains the ability to add content using the Add Box icons depending on the allowAction and showSplitAction settings.
Table 11-3 Actions Settings for Rearranging Content on a Page
| allowAction Setting | showSplitAction Setting | Add Box Icons Enabled? |
|---|---|---|
|
|
|
Yes |
|
|
|
No |
|
|
|
No |
|
|
|
No |
Table 11-4 explains the ability to move content on the page depending on the allowAction and showMoveAction settings.
Table 11-4 Actions Settings for Moving Content on a Page
| allowAction Setting | showMoveAction Setting | Move Content on the Page? |
|---|---|---|
|
|
|
Yes |
|
|
|
No |
|
|
|
No |
|
|
|
No |
Note:
-
If you define security both at the actions category level and actions level and the values for some actions contradict, then a value of
falsetakes precedence overtrue. For example, if you setpersonalizeActionsCategorytotrueandallowActiontofalse, then users cannot add content to their application pages at runtime. Similarly, if you setpersonalizeActionsCategorytofalsebut setallowActiontotrue, then too users cannot add content to their application pages at runtime. -
Restrictions using
showEditActionandshowRemoveActionare applicable only in Design view of a page. That is, if you setshowEditActionandshowRemoveActiononShow Detail Framecomponents tofalse, then users cannot edit or delete such components in Design view of the page. However, users can still select such components in Source view and edit or delete them.
Example 11-5 shows the actions entry that you can add to the customizable components actions section of the adf-config.xml file. You can use EL for element values.
Example 11-5 action Elements in the Customizable Components Security Section
<cust:customizableComponentsSecurity
xmlns="http://xmlns.oracle.com/adf/faces/customizable/config">
<cust:enableSecurity value="true"/>
<cust:actionsCategory>
..........................................
</cust:actionsCategory>
<cust:actions>
<cust:action name="showMinimizeAction" value="true"/>
<cust:action name="showMoveAction" value="false"/>
</cust:actions>
</cust:customizableComponentsSecurity>
11.6 Applying Task Flow Restrictions
Task flow permissions, stored in a secured application's jazn-data.xml file, control the ability to zoom into and edit the task flow in Oracle Composer. By default, no permissions are provisioned on task flows. To enable users to edit a task flow at runtime, you must explicitly grant Edit, Customize, or Grant permission on the page.
Since editing task flow permissions has far reaching impact on the expected task flow editing experience, this capability is disabled by default. To enable task flow permission check, run the server with the following startup parameter:
-Doracle.composer.enableTaskflowPermissionCheck=true
To grant or revoke permissions on a task flow in the jazn-data.xml file:
-
From the Application menu, select Secure, and then ADF Policies.
-
In the
jazn-data.xmlfile, select the task flow in the Overview editor and click the Add button in the Granted to Roles column, shown in Figure 11-10.Figure 11-10 Task Flow Security Region in the jazn-data.xml File

Description of "Figure 11-10 Task Flow Security Region in the jazn-data.xml File "
-
In the Select Roles dialog (Figure 11-11), select the application roles to which you want to grant permissions or create a new role by clicking the Add button.
-
Click OK.
-
Select one or more permissions in the Actions column.
-
Save the
jazn-data.xmlfile.
Note:
The permission grant would appear as follows in the source view of the file:
<permissions>
<permission>
<class>oracle.adf.controller.security.TaskFlowPermission</class>
<name>/WEB-INF/task-flow-definition.xml#task-flow-definition</name>
<actions>customize,view</actions>
</permission>
</permissions>
The TaskFlowPermission class defines task flow-specific actions that it maps to the task flow's operations.
For more information about defining permission grants on task flows, see the section titled "How to Define a Security Policy for ADF Bounded Task Flow" in the Oracle Fusion Middleware Fusion Developer's Guide for Oracle Application Development Framework.
11.7 Troubleshooting Problems with Oracle Composer Components Security
This section provides information to assist you in troubleshooting security-related problems you may encounter while using Oracle Composer components.
For information about configuring logging, see "Configuring ADF Logging for Oracle Composer".
The Show Detail Frame and Panel Customizable do not show the Edit icon, or the Panel Customizable does not show the Add Content button. Also, you are not able to move the Show Detail Frame out of a Panel Customizable component or drop it into another Panel Customizable component.
Ensure that the Panel Customizable is not restricted by using MDS and the component actions are not secured by using entries in adf-config.xml.
You are not able to grant permissions on task flows in the jazn-data.xml file.
Ensure that you run the server with the Java startup parameter, as mentioned in Section 11.6, "Applying Task Flow Restrictions."



