S3L FFT (Fast Fourier Transform)

Complex to Complex FFTs

Sun S3L provides two functions for computing the forward and backward Fourier transforms of one-, two-, and three-dimensional complex arrays: S3L_fft and S3L_ifft.

In Sun S3L, the term forward FFT is used for operations with a negative sign in the exponential factors.

Before calling either of these functions, however, an FFT setup must be computed, using S3L_fft_setup. This setup will contain the FFT twiddle factors and other internal data specific to the algorithm that will be used in the FFT computation.

The setup data depend only on the size, type and layout of the S3L array. Consequently, once they are computed they can be applied in the FFT computation of any other S3L arrays that have the same size, type and layout.

The S3L array must already have been allocated before calling S3L_fft_setup. The setup routine specifies the S3L array of interest by using its array handle, which was returned by a previous call to S3L_declare or S3L_declare_detailed.

The following code example shows S3L_fft_setup being used to create a setup for the S3L array a.

Example 3-1

c
    integer*4 setup_id, ier
    integer*8
c
c compute an FFT setup for a parallel
c S3L array identified by a.
c
c Note that a must have been properly allocated via
c a call to S3L_declare or 3L_declare_detailed.
c
    cakk s3l_fft_setup(a,setup_id,ier)

S3L_fft_setup returns a value of type integer*4 (F77/F90) or int (C/C++) in setup_id. Subsequent calls to S3L_fft and S3L_ifft use the setup_id value to reference the FFT setup of interest.

Use S3L_fft to compute a forward FFT.

call s3l_fft(a,setup_id,ier)

Use S3L_ifft to compute the inverse FFT.

call s3l_ifft(a,setup_id,ier)

Note that the same setup can be used for both the forward and the inverse FFT. S3L_fft does not scale the results, so a forward FFT followed by an inverse FFT results in the original data being scaled by the product of the array extents.

Note also that, for one-dimensional FFTs, there are certain requirements regarding the size of the FFT and the number of processes used to compute it. For details, see "S3L_fft " and "S3L_ifft " or the S3L_fft and S3L_ifft man pages.

S3L_fft and S3L_ifft can be used to compute the Discrete Fourier Transform of arrays of up to three dimensions.

When arrays with more than three dimensions are to be transformed or, when more control over how the FFTs are applied to the array dimensions is desired, use S3L_fft_detailed. This function uses the same setup_id as S3L_fft and S3L_ifft, but accepts additional parameters. S3L_fft_detailed allows the programmer to specify

• the axis along which the transform is to be applied

• the direction of the FFT (1 for forward, -1 for inverse)

Once the FFT computations have completed, the resources associated with that FFT setup should be freed by calling S3L_fft_free_setup, as in the following F77 example.

call s3l_fft_free_setup(setup_id,ier)

Sun S3L FFT Optimizations

The Sun S3L FFT is optimized for use by message-passing applications. It works for S3L arrays with arbitrary distributions a multiprocess process grid. For certain data distributions, maximum efficiency can be obtained.

For example, the algorithm used for a two-dimensional complex-to-complex parallel FFT is optimized for arrays distributed along their second dimension, where the number of processes is a power of two. For maximum efficiency, both axes of the array must be divisible by the number of processes.

When the array distribution allows fast algorithms to be used, the two-dimensional FFT consists essentially of multiple one-dimensional FFTs performed along the array columns local to the process. It then transposes the array in such a way that each process has a number of local rows. This is followed by a second set of local one-dimensional FFTs. Finally, the data are transposed back to the original distribution.

This sequence is illustrated by the diagrams in Figure 3-3 through Figure 3-5.

Figure 3-3 Phase 1 of Two-Dimensional FFT Performing Independent One-Dimensional FFT

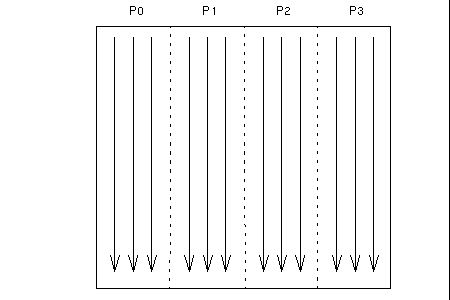
Figure 3-4 Phase 2 of Two-Dimensional FFT Performing Local Transpositions

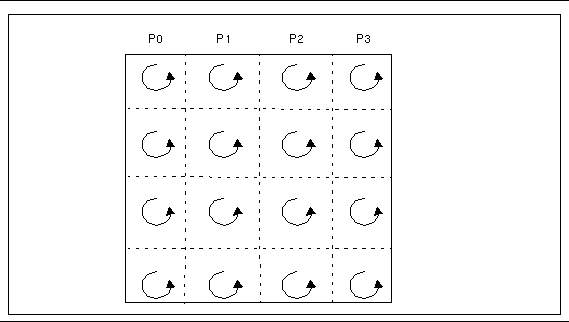
Figure 3-5 Phase 3 of Two-Dimensional FFT Performing Global Transpositions

When the data are distributed in suboptimal ways-- for example, along both dimensions on a rectangular process-grid--a global communication step is usually performed first to redistribute the data to its optimal distribution and then the optimized FFT is performed. This redistribution step increases execution overhead.