| C H A P T E R 2 |
|
IEEE Arithmetic |
This chapter discusses the arithmetic model specified by the ANSI/IEEE Standard 754-1985 for Binary Floating-Point Arithmetic ("the IEEE standard" or "IEEE 754" for short). All SPARC® and x86 processors use IEEE arithmetic. All Sun compiler products support the features of IEEE arithmetic.
This section describes the IEEE 754 specification.
The IEEE single format has a significand precision of 24 bits and occupies 32 bits overall. The IEEE double format has a significand precision of 53 bits and occupies 64 bits overall.
The standard does not prescribe the exact precision and size of these formats, but it does specify the minimum precision and size. For example, an IEEE double extended format must have a significand precision of at least 64 bits and occupy at least 79 bits overall.
The remainder and compare operations must be exact. Each of the other operations must deliver to its destination the exact result, unless there is no such result or that result does not fit in the destination's format. In the latter case, the operation must minimally modify the exact result according to the rules of prescribed rounding modes, presented below, and deliver the result so modified to the operation's destination.
For operands lying within specified ranges, these conversions must produce exact results, if possible, or minimally modify such exact results in accordance with the rules of the prescribed rounding modes. For operands not lying within the specified ranges, these conversions must produce results that differ from the exact result by no more than a specified tolerance that depends on the rounding mode.
The five types of floating-point exceptions are invalid operation, division by zero, overflow, underflow, and inexact.
The IEEE standard also recommends support for user handling of exceptions.
The features required by the IEEE standard make it possible to support interval arithmetic, the retrospective diagnosis of anomalies, efficient implementations of standard elementary functions like exp and cos, multiple precision arithmetic, and many other tools that are useful in numerical computation.
IEEE 754 floating-point arithmetic offers users greater control over computation than does any other kind of floating-point arithmetic. The IEEE standard simplifies the task of writing numerically sophisticated, portable programs not only by imposing rigorous requirements on conforming implementations, but also by allowing such implementations to provide refinements and enhancements to the standard itself.
This section describes how floating-point data is stored in memory. It summarizes the precisions and ranges of the different IEEE storage formats.
A floating-point format is a data structure specifying the fields that comprise a floating-point numeral, the layout of those fields, and their arithmetic interpretation. A floating-point storage format specifies how a floating-point format is stored in memory. The IEEE standard defines the formats, but it leaves to implementors the choice of storage formats.
Assembly language software sometimes relies on using the storage formats, but higher level languages usually deal only with the linguistic notions of floating-point data types. These types have different names in different high-level languages, and correspond to the IEEE formats as shown in TABLE 2-1.
IEEE 754 specifies exactly the single and double floating-point formats, and it defines a class of extended formats for each of these two basic formats. The long double and REAL*16 types shown in TABLE 2-1 refer to one of the class of double extended formats defined by the IEEE standard.
The following sections describe in detail each of the storage formats used for the IEEE floating-point formats on SPARC and x86 platforms.
The IEEE single format consists of three fields: a 23-bit fraction, f; an 8-bit biased exponent, e; and a 1-bit sign, s. These fields are stored contiguously in one 32-bit word, as shown in FIGURE 2-1. Bits 0:22 contain the 23-bit fraction, f, with bit 0 being the least significant bit of the fraction and bit 22 being the most significant; bits 23:30 contain the 8-bit biased exponent, e, with bit 23 being the least significant bit of the biased exponent and bit 30 being the most significant; and the highest-order bit 31 contains the sign bit, s.

TABLE 2-2 shows the correspondence between the values of the three constituent fields s, e and f, on the one hand, and the value represented by the single- format bit pattern on the other; u means don't care, that is, the value of the indicated field is irrelevant to the determination of the value of the particular bit patterns in single format.
Notice that when e < 255, the value assigned to the single format bit pattern is formed by inserting the binary radix point immediately to the left of the fraction's most significant bit, and inserting an implicit bit immediately to the left of the binary point, thus representing in binary positional notation a mixed number (whole number plus fraction, wherein 0 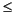 Ò3fraction < 1).
Ò3fraction < 1).
The mixed number thus formed is called the single-format significand. The implicit bit is so named because its value is not explicitly given in the single- format bit pattern, but is implied by the value of the biased exponent field.
For the single format, the difference between a normal number and a subnormal number is that the leading bit of the significand (the bit to left of the binary point) of a normal number is 1, whereas the leading bit of the significand of a subnormal number is 0. Single-format subnormal numbers were called single-format denormalized numbers in IEEE Standard 754.
The 23-bit fraction combined with the implicit leading significand bit provides 24 bits of precision in single-format normal numbers.
Examples of important bit patterns in the single-storage format are shown in TABLE 2-3. The maximum positive normal number is the largest finite number representable in IEEE single format. The minimum positive subnormal number is the smallest positive number representable in IEEE single format. The minimum positive normal number is often referred to as the underflow threshold. (The decimal values for the maximum and minimum normal and subnormal numbers are approximate; they are correct to the number of figures shown.)
|
|
||
|
|
||
A NaN (Not a Number) can be represented with any of the many bit patterns that satisfy the definition of a NaN. The hex value of the NaN shown in TABLE 2-3 is just one of the many bit patterns that can be used to represent a NaN.
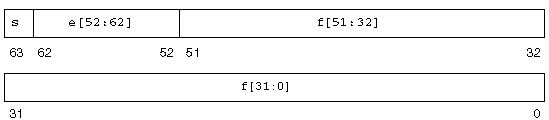
The IEEE double format consists of three fields: a 52-bit fraction, f; an 11-bit biased exponent, e; and a 1-bit sign, s. These fields are stored contiguously in two successively addressed 32-bit words, as shown in FIGURE 2-2.
In the SPARC architecture, the higher address 32-bit word contains the least significant 32 bits of the fraction, while in the x86 architecture the lower address 32-bit word contains the least significant 32 bits of the fraction.
If we denote f[31:0] the least significant 32 bits of the fraction, then bit 0 is the least significant bit of the entire fraction and bit 31 is the most significant of the 32 least significant fraction bits.
In the other 32-bit word, bits 0:19 contain the 20 most significant bits of the fraction, f[51:32], with bit 0 being the least significant of these 20 most significant fraction bits, and bit 19 being the most significant bit of the entire fraction; bits 20:30 contain the 11-bit biased exponent, e, with bit 20 being the least significant bit of the biased exponent and bit 30 being the most significant; and the highest-order bit 31 contains the sign bit, s.
FIGURE 2-2 numbers the bits as though the two contiguous 32-bit words were one 64-bit word in which bits 0:51 store the 52-bit fraction, f; bits 52:62 store the 11-bit biased exponent, e; and bit 63 stores the sign bit, s.
The values of the bit patterns in these three fields determine the value represented by the overall bit pattern.
TABLE 2-4 shows the correspondence between the values of the bits in the three constituent fields, on the one hand, and the value represented by the double-format bit pattern on the other; u means don't care, because the value of the indicated field is irrelevant to the determination of value for the particular bit pattern in double format.
Notice that when e < 2047, the value assigned to the double-format bit pattern is formed by inserting the binary radix point immediately to the left of the fraction's most significant bit, and inserting an implicit bit immediately to the left of the binary point. The number thus formed is called the significand. The implicit bit is so named because its value is not explicitly given in the double-format bit pattern, but is implied by the value of the biased exponent field.
For the double format, the difference between a normal number and a subnormal number is that the leading bit of the significand (the bit to the left of the binary point) of a normal number is 1, whereas the leading bit of the significand of a subnormal number is 0. Double-format subnormal numbers were called double-format denormalized numbers in IEEE Standard 754.
The 52-bit fraction combined with the implicit leading significand bit provides 53 bits of precision in double-format normal numbers.
Examples of important bit patterns in the double-storage format are shown in TABLE 2-5. The bit patterns in the second column appear as two 8-digit hexadecimal numbers. For the SPARC architecture, the left one is the value of the lower addressed 32-bit word, and the right one is the value of the higher addressed 32-bit word, while for the x86 architecture, the left one is the higher addressed word, and the right one is the lower addressed word. The maximum positive normal number is the largest finite number representable in the IEEE double format. The minimum positive subnormal number is the smallest positive number representable in IEEE double format. The minimum positive normal number is often referred to as the underflow threshold. (The decimal values for the maximum and minimum normal and subnormal numbers are approximate; they are correct to the number of figures shown.)
|
|
||
|
|
||
A NaN (Not a Number) can be represented by any of the many bit patterns that satisfy the definition of NaN. The hex value of the NaN shown in TABLE 2-5 is just one of the many bit patterns that can be used to represent a NaN.
The SPARC floating-point environment's quadruple-precision format conforms to the IEEE definition of double-extended format. The quadruple-precision format occupies four 32-bit words and consists of three fields: a 112-bit fraction, f; a 15-bit biased exponent, e; and a 1-bit sign, s. These are stored contiguously as shown in FIGURE 2-3.
The highest addressed 32-bit word contains the least significant 32-bits of the fraction, denoted f[31:0]. The next two 32-bit words contain f[63:32] and f[95:64], respectively. Bits 0:15 of the next word contain the 16 most significant bits of the fraction, f[111:96], with bit 0 being the least significant of these 16 bits, and bit 15 being the most significant bit of the entire fraction. Bits 16:30 contain the 15-bit biased exponent, e, with bit 16 being the least significant bit of the biased exponent and bit 30 being the most significant; and bit 31 contains the sign bit, s.
FIGURE 2-3 numbers the bits as though the four contiguous 32-bit words were one 128-bit word in which bits 0:111 store the fraction, f; bits 112:126 store the 15-bit biased exponent, e; and bit 127 stores the sign bit, s.

The values of the bit patterns in the three fields f, e, and s, determine the value represented by the overall bit pattern.
TABLE 2-6 shows the correspondence between the values of the three constituent fields and the value represented by the bit pattern in quadruple-precision format. u means don't care, because the value of the indicated field is irrelevant to the determination of values for the particular bit patterns.
Examples of important bit patterns in the quadruple-precision double-extended storage format are shown in TABLE 2-7. The bit patterns in the second column appear as four 8-digit hexadecimal numbers. The left-most number is the value of the lowest addressed 32-bit word, and the right-most number is the value of the highest addressed 32-bit word. The maximum positive normal number is the largest finite number representable in the quadruple precision format. The minimum positive subnormal number is the smallest positive number representable in the quadruple precision format. The minimum positive normal number is often referred to as the underflow threshold. (The decimal values for the maximum and minimum normal and subnormal numbers are approximate; they are correct to the number of figures shown.)
|
|
|
|
|
|
|
|
The hex value of the NaN shown in TABLE 2-7 is just one of the many bit patterns that can be used to represent NaNs.
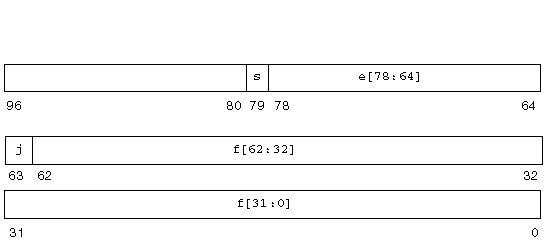
This floating-point environment's double-extended format conforms to the IEEE definition of double-extended formats. It consists of four fields: a 63-bit fraction, f; a 1-bit explicit leading significand bit, j; a 15-bit biased exponent, e; and a 1-bit sign, s.
In the family of x86 architectures, these fields are stored contiguously in ten successively addressed 8-bit bytes. However, the UNIX System V Application Binary Interface Intel 386 Processor Supplement (Intel ABI) requires that double-extended parameters and results occupy three consecutively addressed 32-bit words in the stack, with the most significant 16 bits of the highest addressed word being unused, as shown in FIGURE 2-4.
The lowest addressed 32-bit word contains the least significant 32 bits of the fraction, f[31:0], with bit 0 being the least significant bit of the entire fraction and bit 31 being the most significant of the 32 least significant fraction bits. In the middle addressed 32-bit word, bits 0:30 contain the 31 most significant bits of the fraction, f[62:32], with bit 0 being the least significant of these 31 most significant fraction bits, and bit 30 being the most significant bit of the entire fraction; bit 31 of this middle addressed 32-bit word contains the explicit leading significand bit, j.
In the highest addressed 32-bit word, bits 0:14 contain the 15-bit biased exponent, e, with bit 0 being the least significant bit of the biased exponent and bit 14 being the most significant; and bit 15 contains the sign bit, s. Although the highest order 16 bits of this highest addressed 32-bit word are unused by the family of x86 architectures, their presence is essential for conformity to the Intel ABI, as indicated above.
FIGURE 2-4 numbers the bits as though the three contiguous 32-bit words were one 96-bit word in which bits 0:62 store the 63-bit fraction, f; bit 63 stores the explicit leading significand bit, j; bits 64:78 store the 15-bit biased exponent, e; and bit 79 stores the sign bit, s.
The values of the bit patterns in the four fields f, j, e and s, determine the value represented by the overall bit pattern.
TABLE 2-8 shows the correspondence between the counting number values of the four constituent field and the value represented by the bit pattern. u means don't care, because the value of the indicated field is irrelevant to the determination of value for the particular bit patterns.
Notice that bit patterns in double-extended format do not have an implicit leading significand bit. The leading significand bit is given explicitly as a separate field, j, in the double-extended format. However, when e 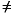 0, any bit pattern with j = 0 is unsupported in the sense that using such a bit pattern as an operand in floating-point operations provokes an invalid operation exception.
0, any bit pattern with j = 0 is unsupported in the sense that using such a bit pattern as an operand in floating-point operations provokes an invalid operation exception.
The union of the disjoint fields j and f in the double extended format is called the significand. When e < 32767 and j = 1, or when e = 0 and j = 0, the significand is formed by inserting the binary radix point between the leading significand bit, j, and the fraction's most significant bit.
In the x86 double-extended format, a bit pattern whose leading significand bit j is 0 and whose biased exponent field e is also 0 represents a subnormal number, whereas a bit pattern whose leading significand bit j is 1 and whose biased exponent field e is nonzero represents a normal number. Because the leading significand bit is represented explicitly rather than being inferred from the value of the exponent, this format also admits bit patterns whose biased exponent is 0, like the subnormal numbers, but whose leading significand bit is 1. Each such bit pattern actually represents the same value as the corresponding bit pattern whose biased exponent field is 1, i.e., a normal number, so these bit patterns are called pseudo-denormals. (Subnormal numbers were called denormalized numbers in IEEE Standard 754.) Pseudo-denormals are merely an artifact of the x86 double-extended format's encoding; they are implicitly converted to the corresponding normal numbers when they appear as operands, and they are never generated as results.
Examples of important bit patterns in the double-extended storage format appear in TABLE 2-9. The bit patterns in the second column appear as one 4-digit hexadecimal counting number, which is the value of the 16 least significant bits of the highest addressed 32-bit word (recall that the most significant 16 bits of this highest addressed 32-bit word are unused, so their value is not shown), followed by two 8-digit hexadecimal counting numbers, of which the left one is the value of the middle addressed 32-bit word, and the right one is the value of the lowest addressed 32-bit word. The maximum positive normal number is the largest finite number representable in the x86 double-extended format. The minimum positive subnormal number is the smallest positive number representable in the double-extended format. The minimum positive normal number is often referred to as the underflow threshold. (The decimal values for the maximum and minimum normal and subnormal numbers are approximate; they are correct to the number of figures shown.)
|
|
|
|
|
|
|
|
A NaN (Not a Number) can be represented by any of the many bit patterns that satisfy the definition of NaN. The hex values of the NaNs shown in TABLE 2-9 illustrate that the leading (most significant) bit of the fraction field determines whether a NaN is quiet (leading fraction bit = 1) or signaling (leading fraction bit = 0).
This section covers the notions of range and precision for a given storage format. It includes the ranges and precisions corresponding to the IEEE single and double formats and to the implementations of IEEE double-extended format on SPARC and x86 architectures. For concreteness, in defining the notions of range and precision we refer to the IEEE single format.
The IEEE standard specifies that 32 bits be used to represent a floating point number in single format. Because there are only finitely many combinations of 32 zeroes and ones, only finitely many numbers can be represented by 32 bits.
What are the decimal representations of the largest and smallest positive numbers that can be represented in this particular format?
Rephrase the question and introduce the notion of range:
What is the range, in decimal notation, of numbers that can be represented by the IEEE single format?
Taking into account the precise definition of IEEE single format, one can prove that the range of floating-point numbers that can be represented in IEEE single format (if restricted to positive normalized numbers) is as follows:
1.175... × (10-38) to 3.402... × (10+38)
A second question refers to the precision (not to be confused with the accuracy or the number of significant digits) of the numbers represented in a given format. These notions are explained by looking at some pictures and examples.
The IEEE standard for binary floating-point arithmetic specifies the set of numerical values representable in the single format. Remember that this set of numerical values is described as a set of binary floating-point numbers. The significand of the IEEE single format has 23 bits, which together with the implicit leading bit, yield 24 digits (bits) of (binary) precision.
One obtains a different set of numerical values by marking the numbers:
(representable by q decimal digits in the significand) on the number line.
FIGURE 2-5 exemplifies this situation:
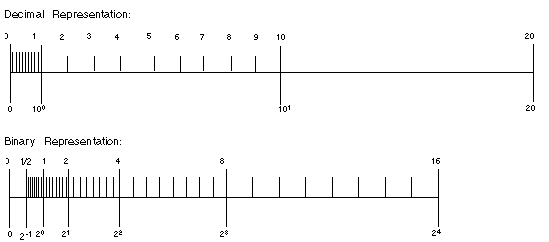
Notice that the two sets are different. Therefore, estimating the number of significant decimal digits corresponding to 24 significant binary digits, requires reformulating the problem.
Reformulate the problem in terms of converting floating-point numbers between binary representations (the internal format used by the computer) and the decimal format (the format users are usually interested in). In fact, you may want to convert from decimal to binary and back to decimal, as well as convert from binary to decimal and back to binary.
It is important to notice that because the sets of numbers are different, conversions are in general inexact. If done correctly, converting a number from one set to a number in the other set results in choosing one of the two neighboring numbers from the second set (which one specifically is a question related to rounding).
Consider some examples. Suppose one is trying to represent a number with the following decimal representation in IEEE single format:
Because there are only finitely many real numbers that can be represented exactly in IEEE single format, and not all numbers of the above form are among them, in general it will be impossible to represent such numbers exactly. For example, let
and run the following Fortran program:
REAL Y, Z Y = 838861.2 Z = 1.3 WRITE(*,40) Y 40 FORMAT("y: ",1PE18.11) WRITE(*,50) Z 50 FORMAT("z: ",1PE18.11) |
The output from this program should be similar to:
The difference between the value 8.388612 × 105 assigned to y and the value printed out is 0.000000125, which is seven decimal orders of magnitude smaller than y. The accuracy of representing y in IEEE single format is about 6 to 7 significant digits, or that y has about six significant digits if it is to be represented in IEEE single format.
Similarly, the difference between the value 1.3 assigned to z and the value printed out is 0.00000004768, which is eight decimal orders of magnitude smaller than z. The accuracy of representing z in IEEE single format is about 7 to 8 significant digits, or that z has about seven significant digits if it is to be represented in IEEE single format.
Assume you convert a decimal floating point number a to its IEEE single format binary representation b, and then translate b back to a decimal number c; how many orders of magnitude are between a and a - c?
What is the number of significant decimal digits of a in the IEEE single format representation, or how many decimal digits are to be trusted as accurate when one represents x in IEEE single format?
The number of significant decimal digits is always between 6 and 9, that is, at least 6 digits, but not more than 9 digits are accurate (with the exception of cases when the conversions are exact, when infinitely many digits could be accurate).
Conversely, if you convert a binary number in IEEE single format to a decimal number, and then convert it back to binary, generally, you need to use at least 9 decimal digits to ensure that after these two conversions you obtain the number you started from.
The complete picture is given in TABLE 2-10:
Base conversion refers to the transformation of a number represented in one base to a number represented in another base. I/O routines such as printf and scanf in C and read, write, and print in Fortran involve base conversion between numbers represented in bases 2 and 10:
In the Solaris environment, the fundamental routines for base conversion in all languages are contained in the standard C library, libc. These routines use table-driven algorithms that yield correctly rounded conversion between any input and output formats subject to modest restrictions on the lengths of the strings of decimal digits involved. In addition to their accuracy, table-driven algorithms reduce the worst-case times for correctly rounded base conversion.
The IEEE standard requires correct rounding for typical numbers whose magnitudes range from 10-44 to 10+44 but permits slightly incorrect rounding for larger exponents. (See section 5.6 of IEEE Standard 754.) The libc table-driven algorithms round correctly throughout the entire range of single, double, and double extended formats.
In C, conversions between decimal strings and binary floating point values are always rounded correctly in accordance with IEEE 754: the converted result is the number representable in the result's format that is nearest to the original value in the direction specified by the current rounding mode. When the rounding mode is round-to-nearest and the original value lies exactly halfway between two representable numbers in the result format, the converted result is the one whose least significant digit is even. These rules apply to conversions of constants in source code performed by the compiler as well as to conversions of data performed by the program using standard library routines.
In Fortran, conversions between decimal strings and binary floating point values are rounded correctly following the same rules as C by default. For I/O conversions, the "round-ties-to-even" rule in round-to-nearest mode can be overridden, either by using the ROUNDING= specifier in the program or by compiling with the -iorounding flag. See the Fortran User's Guide and the f95(1) man page for more information.
See Appendix F for references on base conversion. Particularly good references are Coonen's thesis and Sterbenz's book.
Underflow occurs, roughly speaking, when the result of an arithmetic operation is so small that it cannot be stored in its intended destination format without suffering a rounding error that is larger than usual.
TABLE 2-11 shows the underflow thresholds for single, double, and double-extended precision.
The positive subnormal numbers are those numbers between the smallest normal number and zero. Subtracting two (positive) tiny numbers that are near the smallest normal number might produce a subnormal number. Or, dividing the smallest positive normal number by two produces a subnormal result.
The presence of subnormal numbers provides greater precision to floating-point calculations that involve small numbers, although the subnormal numbers themselves have fewer bits of precision than normal numbers. Producing subnormal numbers (rather than returning the answer zero) when the mathematically correct result has magnitude less than the smallest positive normal number is known as gradual underflow.
There are several other ways to deal with such underflow results. One way, common in the past, was to flush those results to zero. This method is known as Store 0 and was the default on most mainframes before the advent of the IEEE Standard.
The mathematicians and computer designers who drafted IEEE Standard 754 considered several alternatives while balancing the desire for a mathematically robust solution with the need to create a standard that could be implemented efficiently.
IEEE Standard 754 chooses gradual underflow as the preferred method for dealing with underflow results. This method amounts to defining two representations for stored values, normal and subnormal.
Recall that the IEEE format for a normal floating-point number is:
where s is the sign bit, e is the biased exponent, and f is the fraction. Only s, e, and f need to be stored to fully specify the number. Because the implicit leading bit of the significand is defined to be 1 for normal numbers, it need not be stored.
The smallest positive normal number that can be stored, then, has the negative exponent of greatest magnitude and a fraction of all zeros. Even smaller numbers can be accommodated by considering the leading bit to be zero rather than one. In the double-precision format, this effectively extends the minimum exponent from 10-308 to 10-324, because the fraction part is 52 bits long (roughly 16 decimal digits.) These are the subnormal numbers; returning a subnormal number (rather than flushing an underflowed result to zero) is gradual underflow.
Clearly, the smaller a subnormal number, the fewer nonzero bits in its fraction; computations producing subnormal results do not enjoy the same bounds on relative roundoff error as computations on normal operands. However, the key fact about gradual underflow is that its use implies:
Recall that the IEEE format for a subnormal floating-point number is:
where s is the sign bit, the biased exponent e is zero, and f is the fraction. Note that the implicit power-of-two bias is one greater than the bias in the normal format, and the implicit leading bit of the fraction is zero.
Gradual underflow allows you to extend the lower range of representable numbers. It is not smallness that renders a value questionable, but its associated error. Algorithms exploiting subnormal numbers have smaller error bounds than other systems. The next section provides some mathematical justification for gradual underflow.
The purpose of subnormal numbers is not to avoid underflow/overflow entirely, as some other arithmetic models do. Rather, subnormal numbers eliminate underflow as a cause for concern for a variety of computations (typically, multiply followed by add). For a more detailed discussion, see Underflow and the Reliability of Numerical Software by James Demmel and Combatting the Effects of Underflow and Overflow in Determining Real Roots of Polynomials by S. Linnainmaa.
The presence of subnormal numbers in the arithmetic means that untrapped underflow (which implies loss of accuracy) cannot occur on addition or subtraction. If x and y are within a factor of two, then x - y is error-free. This is critical to a number of algorithms that effectively increase the working precision at critical places in algorithms.
In addition, gradual underflow means that errors due to underflow are no worse than usual roundoff error. This is a much stronger statement than can be made about any other method of handling underflow, and this fact is one of the best justifications for gradual underflow.
Most of the time, floating-point results are rounded:
computed result = true result + roundoff
How large can the roundoff be? One convenient measure of its size is called a unit in the last place, abbreviated ulp. The least significant bit of the fraction of a floating-point number in its standard representation is its last place. The value represented by this bit (e.g., the absolute difference between the two numbers whose representations are identical except for this bit) is a unit in the last place of that number. If the computed result is obtained by rounding the true result to the nearest representable number, then clearly the roundoff error is no larger than half a unit in the last place of the computed result. In other words, in IEEE arithmetic with rounding mode to nearest,
Note that an ulp is a relative quantity. An ulp of a very large number is itself very large, while an ulp of a tiny number is itself tiny. This relationship can be made explicit by expressing an ulp as a function: ulp(x) denotes a unit in the last place of the floating-point number x.
Moreover, an ulp of a floating-point number depends on the precision to which that number is represented. For example, TABLE 2-12 shows the values of ulp(1) in each of the four floating-point formats described above:
Recall that only a finite set of numbers can be exactly represented in any computer arithmetic. As the magnitudes of numbers get smaller and approach zero, the gap between neighboring representable numbers narrows. Conversely, as the magnitude of numbers gets larger, the gap between neighboring representable numbers widens.
For example, imagine you are using a binary arithmetic that has only 3 bits of precision. Then, between any two powers of 2, there are 23 = 8 representable numbers, as shown in FIGURE 2-6.
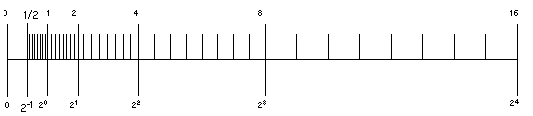
The number line shows how the gap between numbers doubles from one exponent to the next.
In the IEEE single format, the difference in magnitude between the two smallest positive subnormal numbers is approximately 10-45, whereas the difference in magnitude between the two largest finite numbers is approximately 1031!
In TABLE 2-13, nextafter(x,+ ) denotes the next representable number after x as you move along the number line towards +
) denotes the next representable number after x as you move along the number line towards + .
.
Any conventional set of representable floating-point numbers has the property that the worst effect of one inexact result is to introduce an error no worse than the distance to one of the representable neighbors of the computed result. When subnormal numbers are added to the representable set and gradual underflow is implemented, the worst effect of one inexact or underflowed result is to introduce an error no greater than the distance to one of the representable neighbors of the computed result.
In particular, in the region between zero and the smallest normal number, the distance between any two neighboring numbers equals the distance between zero and the smallest subnormal number. The presence of subnormal numbers eliminates the possibility of introducing a roundoff error that is greater than the distance to the nearest representable number.
Because no calculation incurs roundoff error greater than the distance to any of the representable neighbors of the computed result, many important properties of a robust arithmetic environment hold, including these three:
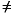 y ⇔ x - y
y ⇔ x - y 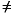 0
0
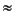 x, to within a rounding error in the larger of x and y
x, to within a rounding error in the larger of x and y
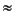 x, when x is a normalized number, implying 1/x
x, when x is a normalized number, implying 1/x 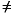 0
0
An alternative underflow scheme is Store 0, which flushes underflow results to zero. Store 0 violates the first and second properties whenever x - y underflows. Also, Store 0 violates the third property whenever 1/x underflows.
Let 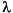 represent the smallest positive normalized number, which is also known as the underflow threshold. Then the error properties of gradual underflow and Store 0 can be compared in terms of
represent the smallest positive normalized number, which is also known as the underflow threshold. Then the error properties of gradual underflow and Store 0 can be compared in terms of 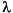 .
.
gradual underflow: |error| < 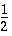 ulp in
ulp in 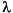
There is a significant difference between half a unit in the last place of 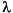 , and
, and 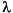 itself.
itself.
The following are two well-known mathematical examples. The first example is code that computes an inner product.
With gradual underflow, the result is as accurate as roundoff allows. In Store 0, a small but nonzero sum could be delivered that looks plausible but is wrong in nearly every digit. However, in fairness, it must be admitted that to avoid just these sorts of problems, clever programmers scale their calculations if they are able to anticipate where minuteness might degrade accuracy.
The second example, deriving a complex quotient, is not amenable to scaling:
It can be shown that, despite roundoff, the computed complex result differs from the exact result by no more than what would have been the exact result if 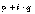 and
and 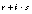 each had been perturbed by no more than a few ulps. This error analysis holds in the face of underflows, except that when both aand bunderflow, the error is bounded by a few ulpsof
each had been perturbed by no more than a few ulps. This error analysis holds in the face of underflows, except that when both aand bunderflow, the error is bounded by a few ulpsof 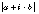 . Neither conclusion is true when underflows are flushed to zero.
. Neither conclusion is true when underflows are flushed to zero.
This algorithm for computing a complex quotient is robust, and amenable to error analysis, in the presence of gradual underflow. A similarly robust, easily analyzed, and efficient algorithm for computing the complex quotient in the face of Store 0 does not exist. In Store 0, the burden of worrying about low-level, complicated details shifts from the implementor of the floating-point environment to its users.
The class of problems that succeed in the presence of gradual underflow, but fail with Store 0, is larger than the fans of Store 0 may realize. Many frequently used numerical techniques fall in this class:
Despite these examples, it can be argued that underflow rarely matters, and so, why bother? However, this argument turns upon itself.
In the absence of gradual underflow, user programs need to be sensitive to the implicit inaccuracy threshold. For example, in single precision, if underflow occurs in some parts of a calculation, and Store 0 is used to replace underflowed results with 0, then accuracy can be guaranteed only to around 10-31, not 10-38, the usual lower range for single-precision exponents.
This means that programmers need to implement their own method of detecting when they are approaching this inaccuracy threshold, or else abandon the quest for a robust, stable implementation of their algorithm.
Some algorithms can be scaled so that computations don't take place in the constricted area near zero. However, scaling the algorithm and detecting the inaccuracy threshold can be difficult and time-consuming for each numerical program.
Copyright © 2005, Sun Microsystems, Inc. All Rights Reserved.