Numerical Computation Guide HomeContentsPreviousNextIndex

Chapter 3

The Math Libraries

This chapter describes the math libraries provided with the Solaris operating environment and Sun WorkShop Compilers. Besides listing each of the libraries along with its contents, this chapter discusses some of the features supported by the math libraries provided with Sun WorkShop Compilers, including IEEE supporting functions, random number generators, and functions that convert data between IEEE and non-IEEE formats.

The contents of the libm and libsunmath libraries are also listed on the intro(3M) man page.

Standard Math Library

The libm math library contains the functions required by the various standards to which the Solaris operating system conforms. This library is bundled with the Solaris operating system in two forms: libm.a, the static version, and libm.so, the shared version.

The default directories for a standard installation of libm are:

/opt/SUNWspro/<release>/lib/libm.a
/opt/SUNWspro/lib/libm.so
/usr/lib/libm.a
/usr/lib/libm.so

The default directories for standard installation of the header files for libm are:

/usr/include/floatingpoint.h
/usr/include/math.h
/usr/include/sys/ieeefp.h

TABLE 3-1 lists the functions in libm.

TABLE 3-1   Contents of libm 
Type Function Name
Algebraic functions cbrt, hypot, sqrt
Elementary transcendental functions asin, acos, atan, atan2, asinh, acosh, atanh, exp, expm1, pow, log, log1p, log10, sin, cos, tan, sinh, cosh, tanh
Higher transcendental functions j0, j1, jn, y0, y1, yn, erf, erfc, gamma, lgamma, gamma_r, lgamma_r
Integral rounding functions ceil, floor, rint
IEEE standard recommended functions copysign, fmod, ilogb, nextafter, remainder, scalbn, fabs
IEEE classification functions isnan
Old style floating-point functions logb, scalb, significand
Error handling routine (user-defined) matherr


Note that the functions gamma_r and lgamma_r are reentrant versions of gamma and lgamma.

As noted above, the standard math library may be installed in two different locations: the libraries located in /usr/lib are bundled with the Solaris operating environment and are installed on all systems, while the libraries located in /opt/SUNWspro are supplied with the Sun WorkShop Compilers and are only available on systems that have access to a compiler installation. While the two sets of libraries provide exactly the same functions with the same interfaces, there are minor differences between the two. First, the functions in the standard math library provided with the compilers may be faster than those in the library bundled with the Solaris operating environment. Second, although both libraries have comparable accuracy, the results delivered by a particular function for a given argument may differ in the least significant bits. Most programs are not particularly sensitive to the numerical differences between these libraries, but the differences can cause minor variations when a program linked with the shared libm.so is run on two different systems, one with the libm.so supplied with the compilers and one with only the default Solaris libm.so. (Minor differences may also be observed when a program is run on systems with different Solaris releases.)

There are several ways to prevent a program from producing varying results depending on the math library it uses.

See the ld(1) and compiler manual pages for more information about dynamic and static linking and the options and environment variables that determine which shared objects are loaded when a program is run.

Additional Math Libraries

Sun Math Library

The library libsunmath is part of the libraries supplied with all Sun language products. The library libsunmath contains a set of functions that were incorporated in previous versions of libm from Sun.

The default directories for a standard installation of libsunmath are:

/opt/SUNWspro/<release>/lib/libsunmath.a
/opt/SUNWspro/lib/libsunmath.so

The default directories for standard installation of the header files for libsunmath are:

/opt/SUNWspro/<release>/include/cc/sunmath.h
/opt/SUNWspro/<release>/include/f77/f77_floatingpoint.h

TABLE 3-2 lists the functions in libsunmath. For each mathematical function, the table gives only the name of the double precision version of the function as it would be called from a C program

TABLE 3-2   Contents of libsunmath  
Type Function Name
Functions from TABLE 3-1 single and extended/quadruple precision available, except for matherr
Elementary transcendental functions exp2, exp10, log2, sincos
Trigonometric functions in degrees asind, acosd, atand, atan2d, sind, cosd, sincosd, tand
Trigonometric functions scaled in 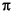asinpi, acospi, atanpi, atan2pi, sinpi, cospi, sincospi, tanpi
Trigonometric functions with double precision argument reduction asinp, acosp, atanp, sinp, cosp, sincosp, tanp
Financial functions annuity, compound
Integral rounding functions aint, anint, irint, nint
IEEE standard recommended functions signbit
IEEE classification functions fp_class, isinf, isnormal, issubnormal, iszero
Functions that supply useful IEEE values min_subnormal, max_subnormal, min_normal, max_normal, infinity, signaling_nan, quiet_nan
Additive random number generators i_addran_, i_addrans_, i_init_addrans_, i_get_addrans_, i_set_addrans_, r_addran_, r_addrans_, r_init_addrans_, r_get_addrans_, r_set_addrans_, d_addran_, d_addrans_, d_init_addrans_, d_get_addrans_, d_set_addrans_, u_addrans_
Linear congruential random number generators i_lcran_, i_lcrans_, i_init_lcrans_, i_get_lcrans_, i_set_lcrans_, r_lcran_, r_lcrans_, d_lcran_, d_lcrans_, u_lcrans_
Multiply-with-carry random number generators i_mwcran_, i_mwcrans_, i_init_mwcrans_, i_get_mwcrans_, i_set_mwcrans, i_lmwcran_, i_lmwcrans_, i_llmwcran_, i_llmwcrans_, u_mwcran_, u_mwcrans_, u_lmwcran_, u_lmwcrans, u_llmwcran_, u_llmwcrans_, r_mwcran_, r_mwcrans_, d_mwcran_, d_mwcrans_, smwcran_
Random number shufflers i_shufrans_, r_shufrans_, d_shufrans_, u_shufrans_
Data conversion convert_external
Control rounding mode and floating-point exception flags ieee_flags
Floating-point trap handling ieee_handler,sigfpe
Show status ieee_retrospective
Enable/disable nonstandard arithmetic standard_arithmetic, nonstandard_arithmetic


.

Optimized Libraries

Optimized versions of some of the routines in libm are provided in the library libmopt. Optimized versions of some of the support routines in libc are provided in the library libcopt. Finally, on SPARC systems, alternate forms of some libc support routines are provided in libcx.

The default directories for a standard installation of libmopt, libcopt, and libcx are:

/opt/SUNWspro/<release>/lib/<arch>/libmopt.a
/opt/SUNWspro/<release>/lib/<arch>/libcopt.a
/opt/SUNWspro/<release>/lib/<arch>/libcx.a (SPARC only)
/opt/SUNWspro/<release>/lib/<arch>/libcx.so.1 (SPARC only)

(Here <arch> denotes one of the architecture-specific library directories. On SPARC, these directories include v7, v8, v8a, v8plus, v8plusa, v8plusb, v9, v9a, and v9b. On x86 platforms, the only directory provided is f80387.)

For a complete description of -xarch, see the Fortran, C, or C++ user's guide.

The routines contained in libcopt are not intended to be called by the user directly. Instead, they replace support routines in libc that are used by the compiler.

The routines contained in libmopt replace corresponding routines in libm. The libmopt versions are generally noticeably faster. Note that unlike the libm versions, which can be configured to provide any of ANSI/POSIX, SVID, X/Open, or IEEE-style treatment of exceptional cases, the libmopt routines only support IEEE-style handling of these cases. (See Appendix E.)

To link with both libmopt and libcopt using cc, give the -lmopt and -lcopt options on the command line. (For best results, put -lmopt immediately before -lm and put -lcopt last.) To link with both libraries using any other compiler, specify the -xlibmopt flag anywhere on the command line.

SPARC: Library libcx contains faster versions of the 128-bit quadruple precision floating point arithmetic support routines. These routines are not intended to be called directly by the user; instead, they are called by the compiler. The Fortran 77 compiler links with libcx automatically unless the -nocx flag is used, but the C compiler does not automatically link with libcx. To use libcx with C programs, link with -lcx.

A shared version of libcx, called libcx.so.1, is also provided. This version can be preloaded at run time by setting the environment variable LD_PRELOAD to the full path name of the libcx.so.1 file. For best performance, use the appropriate version of libcx.so.1 for your system's architecture. For example, on an UltraSPARC system, assuming the library is installed in the default location, set LD_PRELOAD as follows:

csh:

setenv LD_PRELOAD /opt/SUNWspro/lib/v8plus/libcx.so.1

sh:

LD_PRELOAD=/opt/SUNWspro/lib/v8plus/libcx.so.1 export LD_PRELOAD

Vector Math Library (SPARC only)

On SPARC platforms, the library libmvec provides routines that evaluate common mathematical functions for an entire vector of arguments.

The default directory for a standard installation of libmvec is:

/opt/SUNWspro/<release>/lib/<arch>/libmvec.a
/opt/SUNWspro/<release>/lib/<arch>/libmvec_mt.a

TABLE 3-3 lists the functions in libmvec.

TABLE 3-3   Contents of libmvec
Type Function Name
Algebraic functions vhypot_, vhypotf_, vc_abs_, vz_abs_
Exponential and related functions vexp_, vexpf_, vlog_, vlogf_, vpow_, vpowf_, vc_exp_, vz_exp_, vc_log_, vz_log_, vc_pow_, vz_pow_
Trigonometric functions vatan_, vatanf_, vatan2_, vatan2f_, vcos_, vcosf_, vsin_, vsinf_, vsincos_, vsincosf_


Note that libmvec_mt.a provides parallel versions of the vector functions that rely on multiprocessor parallelization. To use libmvec_mt.a, you must link with -xparallel.

See the libmvec(3m) and clibmvec(3m) manual pages for more information.

libm9x Math Library

The libm9x math library contains some of the math and floating-point related functions specified in C99. In the Sun Workshop 6 compilers release, this library contains the <fenv.h> Floating-Point Environment functions as well as enhancements to support improved handling of floating-point exceptions.

The default directory for a standard installation of libm9x is:

/opt/SUNWspro/lib/libm9x.so

The default directories for standard installation of the header files for libm9x are:

/opt/SUNWspro/<release>/include/cc/fenv.h
/opt/SUNWspro/<release>/include/cc/fenv96.h

TABLE 3-4 lists the functions in libm9x. (The precision control functions fegetprec and fesetprec are available only on x86 platforms.)

TABLE 3-4   Contents of libm9x
Type Function Name
C99 standard floating point environment functions feclearexcept, fegetenv, fegetexceptflag, fegetround, feholdexcept, feraiseexcept, fesetenv, fesetexceptflag, fesetround, fetestexcept, feupdateenv
Precision control (x86) fegetprec, fesetprec
Exception handling and retrospective diagnostics fex_get_handling, fex_get_log, fex_getexcepthandler, fex_log_entry, fex_merge_flags, fex_set_handling, fex_set_log, fex_setexcepthandler


Note that libm9x is provided as a shared library only. The cc compiler does not automatically search for libraries in the shared library installation directory when linking. Therefore, to link with libm9x using cc, you must enable both the static linker and the run-time linker to locate the library. You can enable the static linker to locate libm9x in one of three ways:

You can enable the run-time linker to locate libm9x in one of three ways:

All other Sun Workshop Compilers automatically search the shared library installation directory. To link with libm9x using any of these compilers, simply specify -lm9x on the command line. (While libm9x is primarily intended to be used with C/C++ programs, it is possible to use it with Fortran programs; see Appendix A for an example.)

Single, Double, and Long Double Precision

Most numerical functions are available in single, double, and long-double precision. Examples of calling different precision versions from different languages are shown in TABLE 3-5.

TABLE 3-5   Calling Single, Double, and Quadruple Functions
Language Single Double Quadruple
C, C++ #include <sunmath.h>
float x,y,z;
x = sinf(y);
x = fmodf(y,z);
x = max_normalf();
x = r_addran_(); 		#include <math.h>
double x,y,z;
x = sin(y);
x = fmod(y,z);

#include <sunmath.h>
double x,y,z;
x = max_normal();
x = d_addran_(); 		#include <sunmath.h>
long double x,y,z;
x = sinl(y);
x = fmodl(y,z);
x = max_normall();
Fortran REAL x,y,z
x = sin(y)
x = r_fmod(y,z)
x = r_max_normal()
x = r_addran() 		REAL*8 x,y,z
x = sin(y)
x = d_fmod(y,z)
x = d_max_normal()
x = d_addran() 		REAL*16 x,y,z
x = sin(y)
x = q_fmod(y,z)
x = q_max_normal()


In C, names of single-precision functions are formed by appending f to the double-precision name, and names of quadruple-precision functions are formed by adding l. Because Fortran calling conventions differ, libsunmath provides r_..., d_..., and q_... versions for single, double, and quadruple precision functions, respectively. Fortran intrinsic functions can be called by the generic name for all three precisions.

Not all functions have q_... versions. Refer to math.h and sunmath.h for names and definitions of libm and libsunmath functions.

In Fortran programs, remember to declare r_... functions as real, d_... functions as double precision, and q_... functions as real*16. Otherwise, type mismatches might result.

Note – The x86 edition of Fortran supports real and double precision only; it does not support REAL*16. The x86 edition of C, however, supports long double.

IEEE Support Functions

This section describes the IEEE recommended functions, the functions that supply useful values, ieee_flags, ieee_retrospective, and standard_arithmetic and nonstandard_arithmetic. Refer to Chapter 4 for more information on the functions ieee_flags and ieee_handler.

ieee_functions(3m) and ieee_sun(3m)

The functions described by ieee_functions(3m) and ieee_sun(3m) provide capabilities either required by the IEEE standard or recommended in its appendix. These are implemented as efficient bit mask operations.

TABLE 3-6   ieee_functions(3m)  
Function Description
math.h Header file
copysign(x,y) x with y's sign bit
fabs(x) Absolute value of x
fmod(x, y) Remainder of x with respect to y
ilogb(x) Base 2 unbiased exponent of x in integer format
nextafter(x,y) Next representable number after x, in the direction y
remainder(x,y) Remainder of x with respect to y
scalbn(x,n) x × 2n


TABLE 3-7   ieee_sun(3m)  
Function Description
sunmath.h Header file
fp_class(x) Classification function
isinf(x) Classification function
isnormal(x) Classification function
issubnormal(x) Classification function
iszero(x) Classification function
signbit(x) Classification function
nonstandard_arithmetic(void) Toggle hardware
standard_arithmetic(void) Toggle hardware
ieee_retrospective(*f)


The remainder(x,y) is the operation specified in IEEE Standard 754-1985. The difference between remainder(x,y) and fmod(x,y) is that the sign of the result returned by remainder(x,y) might not agree with the sign of either x or y, whereas fmod(x,y) always returns a result whose sign agrees with x. Both functions return exact results and do not generate inexact exceptions.

TABLE 3-8   Calling ieee_functions from Fortran
IEEE Function Single Precision Double Precision Quadruple Precision
copysign(x,y) t=r_copysign(x,y) z=d_copysign(x,y) z=q_copysign(x,y)
ilogb(x) i=ir_ilogb(x) i=id_ilogb(x) i=iq_ilogb(x)
nextafter(x,y) t=r_nextafter(x,y) z=d_nextafter(x,y) z=q_nextafter(x,y)
scalbn(x,n) t=r_scalbn(x,n) z=d_scalbn(x,n) z=q_scalbn(x,n)
signbit(x) i=ir_signbit(x) i=id_signbit(x) i=iq_signbit(x)


TABLE 3-9   

IEEE Function Single Precision Double Precision Quadruple Precision
signbit(x) i=ir_signbit(x) i=id_signbit(x) i=iq_signbit(x)


Calling ieee_sun from Fortran

Note – You must declare d_function as double precision and q_function as REAL*16 in the Fortran program that uses them.

ieee_values(3m)

IEEE values like infinity, NaN, maximum and minimum positive floating-point numbers are provided by the functions described by the ieee_values(3m) man page. TABLE 3-10, TABLE 3-11, TABLE 3-12, and TABLE 3-12 show the decimal values and hexadecimal IEEE representations of the values provided by ieee_values(3m) functions.

TABLE 3-10   IEEE Values: Single Precision 
IEEE value Decimal value
hexadecimal representation		 C, C++
Fortran
max normal 3.40282347e+38
7f7fffff 		r = max_normalf();
r = r_max_normal()
min normal 1.17549435e-38
00800000 		r = min_normalf();
r = r_min_normal()
max subnormal 1.17549421e-38
007fffff 		r = max_subnormalf();
r = r_max_subnormal()
min subnormal 1.40129846e-45
00000001 		r = min_subnormalf();
r = r_min_subnormal()
Infinity
7f800000 		r = infinityf();
r = r_infinity()
quiet NaN NaN
7fffffff 		r = quiet_nanf(0);
r = r_quiet_nan(0)
signaling NaN NaN
7f800001 		r = signaling_nanf(0);
r = r_signaling_nan(0)


TABLE 3-11   IEEE Values: Double Precision 
IEEE value Decimal Value
hexadecimal representation 		C, C++
Fortran
max normal 1.7976931348623157e+308
7fefffff ffffffff 		d = max_normal();
d = d_max_normal()
min normal 2.2250738585072014e-308
00100000 00000000 		d = min_normal();
d = d_min_normal()
max subnormal 2.2250738585072009e-308
000fffff ffffffff 		d = max_subnormal();
d = d_max_subnormal()
min subnormal 4.9406564584124654e-324
00000000 00000001 		d = min_subnormal();
d = d_min_subnormal()
Infinity
7ff00000 00000000 		d = infinity();
d = d_infinity()
quiet NaN NaN
7fffffff ffffffff 		d = quiet_nan(0);
d = d_quiet_nan(0)
signaling NaN NaN
7ff00000 00000001 		d = signaling_nan(0);
d = d_signaling_nan(0)


TABLE 3-12   IEEE Values: Quadruple Precision (SPARC)

IEEE value Decimal value
hexadecimal representation		 C, C++
Fortran
max normal 1.1897314953572317650857593266280070e+4932
7ffeffff ffffffff ffffffff ffffffff 		q = max_normall();
q = q_max_normal()
min normal 3.3621031431120935062626778173217526e-4932
00010000 00000000 00000000 00000000 		q = min_normall();
q = q_min_normal()
max subnormal 3.3621031431120935062626778173217520e-4932
0000ffff ffffffff ffffffff ffffffff 		q = max_subnormall();
q = q_max_subnormal()
min subnormal 6.4751751194380251109244389582276466e-4966
00000000 00000000 00000000 00000001 		q = min_subnormall();
q = q_min_subnormal()
Infinity
7fff0000 00000000 00000000 00000000 		q = infinityl();
q = q_infinity()
quiet NaN NaN
7fff8000 00000000 00000000 00000000 		q = quiet_nanl(0);
q = q_quiet_nan(0)
signaling NaN NaN
7fff0000 00000000 00000000 00000001 		q = signaling_nanl(0);
q = q_signaling_nan(0)


TABLE 3-13   IEEE Values: Double Extended Precision (x86)  
IEEE value Decimal value
hexadecimal representation (80 bits)		 C, C++
max normal 1.18973149535723176505e+4932
7ffe ffffffff ffffffff 		x = max_normall();
min positive normal 3.36210314311209350626e-4932
0001 80000000 00000000 		x = min_normall();
max subnormal 3.36210314311209350608e-4932
0000 7fffffff ffffffff 		x = max_subnormall();
min positive subnormal 1.82259976594123730126e-4951
0000 00000000 00000001 		x = min_subnormall();
Infinity
7fff 80000000 00000000 		x = infinityl();
quiet NaN NaN
7fff c0000000 00000000 		x = q
signaling NaN NaN
7fff 80000000 00000001 		x = signaling_nanl(0);


ieee_flags(3m)

ieee_flags (3m) is the Sun interface to:

The syntax for a call to ieee_flags(3m) is:

i = ieee_flags(action, mode, in, out);

The ASCII strings that are the possible values for the parameters are shown in TABLE 3-14:

TABLE 3-14   Parameter Values for ieee_flags
Parameter C or C++ Type All Possible Values
action char * get, set, clear, clearall
mode char * direction, precision, exception
in char * nearest, tozero, negative, positive, extended, double, single, inexact, division, underflow, overflow, invalid, all, common
out char ** nearest, tozero, negative, positive, extended, double, single, inexact, division, underflow, overflow, invalid, all, common


The ieee_flags(3m) man page describes the parameters in complete detail.

Some of the arithmetic features that can be modified by using ieee_flags are covered in the following paragraphs. Chapter 4 contains more information on ieee_flags and IEEE exception flags.

When mode is direction, the specified action applies to the current rounding direction. The possible rounding directions are: round towards nearest, round towards zero, round towards +, or round towards -. The IEEE default rounding direction is round towards nearest. This means that when the mathematical result of an operation lies strictly between two adjacent representable numbers, the one nearest to the mathematical result is delivered. (If the mathematical result lies exactly halfway between the two nearest representable numbers, then the result delivered is the one whose least significant bit is zero. The round towards nearest mode is sometimes called round to nearest even to emphasize this.)

Rounding towards zero is the way many pre-IEEE computers work, and corresponds mathematically to truncating the result. For example, if 2/3 is rounded to 6 decimal digits, the result is .666667 when the rounding mode is round towards nearest, but .666666 when the rounding mode is round towards zero.

When using ieee_flags to examine, clear, or set the rounding direction, possible values for the four input parameters

TABLE 3-15   ieee_flags Input Values for the Rounding Direction
Parameter Possible value (mode is direction)
action get, set, clear, clearall
in nearest, tozero, negative, positive
out nearest, tozero, negative, positive


are shown in TABLE 3-15.

When mode is precision, the specified action applies to the current rounding precision. On x86 platforms, the possible rounding precisions are: single, double, and extended. The default rounding precision is extended; in this mode, arithmetic operations that deliver a result to a floating point register round their result to the full 64-bit precision of the extended double register format. When the rounding precision is single or double, arithmetic operations that deliver a result to a floating point register round their result to 24 or 53 significant bits, respectively. Although most programs produce results that are at least as accurate, if not more so, when extended rounding precision is used, some programs that require strict adherence to the semantics of IEEE arithmetic will not work correctly in extended rounding precision mode and must be run with the rounding precision set to single or double as appropriate.

Rounding precision cannot be set on systems using SPARC processors. On these systems, calling ieee_flags with mode = precision has no effect on computation.

Finally, when mode is exception, the specified action applies to the current IEEE exception flags. See Chapter 4 for more information about using ieee_flags to examine and control the IEEE exception flags.

ieee_retrospective(3m)

The libsunmath function ieee_retrospective prints information about unrequited exceptions and nonstandard IEEE modes. It reports:

The necessary information is obtained from the hardware floating-point status register.

ieee_retrospective prints information about exception flags that are raised, and exceptions for which a trap is enabled. These two distinct, if related, pieces of information should not be confused. If an exception flag is raised, then that exception occurred at some point during program execution. If a trap is enabled for an exception, then the exception may not have actually occurred (but if it had, a SIGFPE signal would have been delivered). The ieee_retrospective message is meant to alert you about exceptions that may need to be investigated (if the exception flag is raised), or to remind you that exceptions may have been handled by a signal handler (if the exception's trap is enabled.) Chapter 4 discusses exceptions, signals, and traps, and shows how to investigate the cause of a raised exception.

ieee_retrospective can be called anytime, but it is usually called before exit points. Programs compiled with f77 call ieee_retrospective on exit by default.

The syntax for calling this function is:

C, C++ ieee_retrospective(fp);
Fortran call ieee_retrospective()

For the C function, the argument fp specifies the file to which the output will be written. The Fortran function always prints output on stderr.

The following example shows four of the six ieee_retrospective warning messages: 

 Note: IEEE floating-point exception flags raised:  

    Inexact; Underflow; 

 Rounding direction toward zero 

 IEEE floating-point exception traps enabled: 

    overflow; 

 See the Numerical Computation Guide, ieee_flags(3M), 

    ieee_handler(3M), ieee_sun(3m)

A warning message appears only if trapping is enabled or an exception was raised.

You can suppress ieee_retrospective messages from Fortran programs by one of three methods. One approach is to clear all outstanding exceptions, disable traps, and restore round-to-nearest, extended precision, and standard modes before the program exits. To do this, call ieee_flags, ieee_handler, and standard_arithmetic as follows:

character*8 out 

i = ieee_flags('clearall', '', '', out) 

call ieee_handler('clear', 'all', 0)

call standard_arithmetic()

Note – Clearing outstanding exceptions without investigating their cause is not recommended.

Another way to avoid seeing ieee_retrospective messages is to redirect stderr to a file. Of course, this method should not be used if the program sends output other than ieee_retrospective messages to stderr.

The third approach is to include a dummy ieee_retrospective function in the program, for example:

subroutine ieee_retrospective

return

end

nonstandard_arithmetic(3m)

As discussed in Chapter 2, IEEE arithmetic handles underflowed results using gradual underflow. On some SPARC systems, gradual underflow is often implemented partly with software emulation of the arithmetic. If many calculations underflow, this may cause performance degradation.

To obtain some information about whether this is a case in a specific program, you can use ieee_retrospective or ieee_flags to determine if underflow exceptions occur, and check the amount of system time used by the program. If a program spends an unusually large amount of time in the operating system, and raises underflow exceptions, gradual underflow may be the cause. In this case, using non-IEEE arithmetic may speed up program execution.

The function nonstandard_arithmetic causes underflowed results to be flushed to zero on those SPARC implementations that have a mode in hardware in which flushing to zero is faster. The trade-off for speed is accuracy, because the benefits of gradual underflow are lost.

The function standard_arithmetic resets the hardware to use the default IEEE arithmetic. Both functions have no effect on implementations that provide only the default IEEE 754 style of arithmetic--SuperSPARCTM is such an implementation.

C99 Floating Point Environment Functions

This section describes the <fenv.h> floating point environment functions in C99. In the Sun WorkShop 6 compilers release, these functions are available in the libm9x.so library. They provide many of the same capabilities as the ieee_flags function, but they use a more natural C interface, and because they are defined by C99, they may prove to be more portable in the future.

Note – For consistent behavior, do not use both C99 floating point environment functions and exception handling extensions in libm9x.so and the ieee_flags and ieee_handler functions in libsunmath in the same program.

Exception Flag Functions

The fenv.h file defines macros for each of the five IEEE floating point exception flags: FE_INEXACT, FE_UNDERFLOW, FE_OVERFLOW, FE_DIVBYZERO, and FE_INVALID. In addition, the macro FE_ALL_EXCEPT is defined to be the bitwise "or" of all five flag macros. In the following descriptions, the excepts parameter may be a bitwise "or" of any of the five flag macros or the value FE_ALL_EXCEPT. For the fegetexceptflag and fesetexceptflag functions, the flagp parameter must be a pointer to an object of type fexcept_t. (This type is defined in fenv.h.)

C99 defines the following exception flag functions:

TABLE 3-16   C99 Standard Exception Flag Functions
Function Action 
feclearexcept(excepts)
clear specified flags 
fetestexcept(excepts)
return settings of specified flags 
feraiseexcept(excepts)
raise specified exceptions 
fegetexceptflag(flagp, excepts)
save specified flags in *flagp 
fesetexceptflag(flagp, excepts)
restore specified flags from *flagp


The feclearexcept function clears the specified flags. The fetestexcept function returns a bitwise "or" of the macro values corresponding to the subset of flags specified by the excepts argument that are set. For example, if the only flags currently set are inexact, underflow, and division by zero, then 

     i = fetestexcept(FE_INVALID | FE_DIVBYZERO);

would set i to FE_DIVBYZERO.

The feraiseexcept function causes a trap if any of the specified exceptions' trap is enabled. (See Chapter 4 for more information on exception traps.) Otherwise, it merely sets the corresponding flags.

The fegetexceptflag and fesetexceptflag functions provide a convenient way to temporarily save the state of certain flags and later restore them. In particular, the fesetexceptflag function does not cause a trap; it merely restores the values of the specified flags.

Rounding Control

The fenv.h file defines macros for each of the four IEEE rounding direction modes: FE_TONEAREST, FE_UPWARD (toward positive infinity), FE_DOWNWARD (toward negative infinity), and FE_TOZERO. C99 defines two functions to control rounding direction modes: fesetround sets the current rounding direction to the direction specified by its argument (which must be one of the four macros above), and fegetround returns the value of the macro corresponding to the current rounding direction.

On x86 platforms, the fenv.h file defines macros for each of three rounding precision modes: FE_FLTPREC (single precision), FE_DBLPREC (double precision), and FE_LDBLPREC (extended double precision). Although they are not part of C99, libm9x.so on x86 provides two functions to control the rounding precision mode: fesetprec sets the current rounding precision to the precision specified by its argument (which must be one of the three macros above), and fegetprec returns the value of the macro corresponding to the current rounding precision.

Environment Functions

The fenv.h file defines the data type fenv_t, which represents the entire floating point environment including exception flags, rounding control modes, exception handling modes, and, on SPARC, nonstandard mode. In the descriptions that follow, the envp parameter must be a pointer to an object of type fenv_t.

C99 defines four functions to manipulate the floating point environment. libm9x.so provides an additional function that may be useful in multi-threaded programs. These functions are summarized in the following table:

TABLE 3-17   libm9x.so Floating Point Environment Functions
Function Action
fegetenv(envp) save environment in *envp
fesetenv(envp) restore environment from *envp
feholdexcept(envp) save environment in *envp and establish nonstop mode
feupdateenv(envp) restore environment from *envp and raise exceptions
fex_merge_flags(envp) "or" exception flags from *envp


The fegetenv and fesetenv functions respectively save and restore the floating point environment. The argument to fesetenv may be either a pointer to an environment previously saved by a call to fegetenv or feholdexcept or the constant FE_DFL_ENV defined in fenv.h. The latter represents the default environment with all exception flags clear, rounding to nearest (and to extended double precision on x86), nonstop exception handling mode (i.e., traps disabled), and on SPARC, nonstandard mode disabled.

The feholdexcept function saves the current environment and then clears all exception flags and establishes nonstop exception handling mode for all exceptions. The feupdateenv function restores a saved environment (which may be one saved by a call to fegetenv or feholdexcept or the constant FE_DFL_ENV), then raises those exceptions whose flags were set in the previous environment. If the restored environment has traps enabled for any of those exceptions, a trap occurs; otherwise the flags are set. These two functions may be used in conjunction to make a subroutine call appear to be atomic with regard to exceptions, as the following code sample shows: 

#include <fenv.h>

 

void myfunc(...) {

 

    fenv_t env;

 

 

    /* save the environment, clear flags, and disable traps */

 

    feholdexcept(&env);

 

    /* do a computation that may incur exceptions */

 

    ...

 

    /* check for spurious exceptions */

 

    if (fetestexcept(...)) {

 

        /* handle them appropriately and clear their flags */

 

        ...

 

        feclearexcept(...);

 

    }

 

    /* restore the environment and raise relevant exceptions */

 

    feupdateenv(&env);

 

}


  







 






   The fex_merge_flags function performs a logical OR of the exception flags from the saved environment into the current environment without provoking any traps. This function may be used in a multi-threaded program to preserve information in the parent thread about flags that were raised by a computation in a child thread. See Appendix A for an example showing the use of fex_merge_flags.






   Implementation Features of libm and libsunmath 






   This section describes implementation features of libm and libsunmath: 






   About the Algorithms 






   The elementary functions in libm and libsunmath on SPARC systems are implemented with an ever-changing combination of table-driven and polynomial/rational approximation algorithms. Some elementary functions in libm and libsunmath on x86 platforms are implemented using the elementary function kernel instructions provided in the x86 instruction set; other functions are implemented using the same table-driven or polynomial/rational approximation algorithms used on SPARC.






   Both the table-driven and polynomial/rational approximation algorithms for the common elementary functions in libm and the common single precision elementary functions in libsunmath deliver results that are accurate to within one unit in the last place (ulp). On SPARC, the common quadruple precision elementary functions in libsunmath deliver results that are accurate to within one ulp, except for the expm1l and log1pl functions, which deliver results accurate to within two ulps. (The common functions include the exponential, logarithm, and power functions and circular trigonometric functions of radian arguments. Other functions, such as the hyperbolic trig functions and higher transcendental functions, are less accurate.) These error bounds have been obtained by direct analysis of the algorithms. Users can also test the accuracy of these routines using BeEF, the Berkeley Elementary Function test programs, available from netlib in the ucbtest package (http://www.netlib.org/fp/ucbtest.tgz).






   Argument Reduction for Trigonometric Functions 






   Trigonometric functions for radian arguments outside the range [-/4,/4] are usually computed by reducing the argument to the indicated range by subtracting integral multiples of /2. 






   Because  is not a machine-representable number, it must be approximated. The error in the final computed trigonometric function depends on the rounding errors in argument reduction (with an approximate  as well as the rounding), and approximation errors in computing the trigonometric function of the reduced argument. Even for fairly small arguments, the relative error in the final result might be dominated by the argument reduction error, while even for fairly large arguments, the error due to argument reduction may be no worse than the other errors. 






   There is widespread misapprehension that trigonometric functions of all large arguments are inherently inaccurate, and all small arguments relatively accurate. This is based on the simple observation that large enough machine-representable numbers are separated by a distance greater than . 






   There is no inherent boundary at which computed trigonometric function values suddenly become bad, nor are the inaccurate function values useless. Provided that the argument reduction is done consistently, the fact that the argument reduction is performed with an approximation to  is practically undetectable, because all essential identities and relationships are as well preserved for large arguments as for small. 






   libm and libsunmath trigonometric functions use an "infinitely" precise  for argument reduction. The value 2/ is computed to 916 hexadecimal digits and stored in a lookup table to use during argument reduction. 






   The group of functions sinpi, cospi, and tanpi (see TABLE 3-2) scales the input argument by  to avoid inaccuracies introduced by range reduction. 






   Data Conversion Routines 






   In libm and libsunmath, there is a flexible data conversion routine, convert_external, used to convert binary floating-point data between IEEE and non-IEEE formats. 






   Formats supported include those used by SPARC (IEEE), IBM PC, VAX, IBM S/370, and Cray. 






   Refer to the man page on convert_external(3m) for an example of taking data generated on a Cray, and using the function convert_external to convert the data into the IEEE format expected on SPARC systems. 






   Random Number Facilities






   There are three facilities for generating uniform pseudo-random numbers in 32-bit integer, single precision floating point, and double precision floating point formats:






   In addition, the functions described on the shufrans(3m) manual page may be used in conjunction with any of these generators to shuffle an array of pseudo-random numbers, thereby providing even more randomness for applications that need it. (Note that there is no facility for shuffling arrays of 64-bit integers.)






   Each of the random number facilities includes routines that generate one random number at a time (i.e., one per function call) as well as routines that generate an array of random numbers in a single call. The functions that generate one random number at a time deliver numbers that lie in the ranges shown in TABLE 3-18



    

   TABLE 3-18 	  Intervals for Single-Value Random Number Generators
  
 Function
     Lower Bound
     Upper Bound
  

  

    
 i_addran_

    
 -2147483648

    
 2147483647

  

  

    
 r_addran_

    
 0

    
 0.9999999403953552246

  

  

    
 d_addran_

    
 0

    
 0.9999999999999998890

  

  

    
 i_lcran_

    
 1

    
 2147483646

  

  

    
 r_lcran_

    
 4.656612873077392578E-10

    
 1

  

  

    
 d_lcran_

    
 4.656612875245796923E-10

    
 0.9999999995343387127

  

  

    
 i_mwcran_

    
 0

    
 2147483647

  

  

    
 u_mwcran_

    
 0

    
 4294967295

  

  

    
 i_llmwcran_

    
 0

    
 9223372036854775807

  

  

    
 u_llmwcran_

    
 0

    
 18446744073709551615

  

  

    
 r_mwcran_

    
 0

    
 0.9999999403953552246

  

  

    
 d_mwcran_

    
 0

    
 0.9999999999999998890

  








. 






   The functions that generate an entire array of random numbers in a single call allow the user to specify the interval in which the generated numbers will lie. Appendix A gives several examples that show how to generate arrays of random numbers uniformly distributed over different intervals.






   Note that the addrans and mwcrans generators are generally more efficient than the lcrans generators, but their theory is not as refined. "Random Number Generators: Good Ones Are Hard To Find", by S. Park and K. Miller, Communications of the ACM, October 1988, discusses the theoretical properties of linear congruential algorithms. Additive random number generators are discussed in Volume 2 of Knuth's The Art of Computer Programming. 






   

















Sun Microsystems, Inc.

Copyright information. All rights reserved.

Feedback






Library
  |  
Contents
  |  
Previous
  |  
Next
  |  
Index