| Fortran 95 ��ֱ黻�ץ�����ߥ�ե���� |
�Ѹ콸
- �ط��黻��: certainly true (relational operators: certainly true) �Ȥ��Ƥ���������
- cset(expression, set)��ɽ���ϡ����Ȥΰ��������Ф���ɾ������뼰��������Ū��ɽ������˻��Ѥ��ޤ������Ȥ��С��� f(x, y) = xy �ˤĤ��ơ���ּ�[0] [0] × [+
] ���������ʤ���Фʤ�ʤ���ޤ�����ϡ����Τ褦��ɽ����ޤ���
- [0] × [+
]
cset(x × y, {(0,+
)}) = [-
, +
].
- ev (literal_constant) ��ɽ���ϥ�ƥ�����ʸ����ˤ��������줿�����ͤ�ɽ���Τ˻��Ѥ��ޤ������Ȥ��С���� 0.1 �ϥޥ���ɽ���Ǥ��ʤ��Τǡ�0.1 ������Ū�ʶ���ͤ��Ȥ��ʤ���Фʤ�ʤ��Ȥ������¤˴ط��ʤ���ev(0.1) = 1/10 �Ȥʤ�ޤ���
f95�Ǥϡ�INTERVAL ��ͭ�δؿ���ɸ�� Fortran �ؿ��ζ�֥С������ǤϤʤ�����ִؿ��Ǥ������Ȥ��С�WID��MID��INF��SUP��INTERVAL��ͭ�δؿ��Ǥ���
- ���̷��ѥ����� (KTPV) �Ȥ��Ƥ���������
- ��ּ��κ������ἰ�����Τ�ȤǤϡ����٤Ƥζ�֤ϼ������Ǥ�դΥǡ������ܤ� KTPV �κ����ͤؤ��Ѵ�����ޤ������κ����ͤˤϡ�KTPVmax �Ȥ���̾����Ϳ�����Ƥ��ޤ���
- KTPV ����ζ�ּ��ϰۤʤ� KTPV ���������� (�ޤ���) �ѿ���ޤߤޤ������Ȥ��С�[1_4] + [0.2_8] ��KTPV ����ζ�ּ��Ǥ����������ἰ�����Τ�ȤǤϡ�KTPV ����ζ�ּ���������ޤ�������̩�������Τ�ȤǤϵ�����ޤ���
- �ط��黻��: possibly true (relational operators: possibly true) �Ȥ��Ƥ���������
- Fortran �Ǥϡ�����ʸ�ϼ����ͤ��ͤ������黻�� = �α�¦�Ƿ�������¦���ѿ����������ǡ��ޤ��ϡ�����˳�Ǽ���ޤ���
- Fortran ��ƥ������γ����ͤϡ���ƥ�������ʸ����ˤ��������줿����Ū���ͤǤ�����ƥ������γ����ͤ����������Ū�ʶ���ͤ�Ʊ���Ǥ���Ȥϸ¤�ޤ���Ԥϡ�Fortran ɸ��Ǥϥ�ƥ�������ͣ���������줿�ͤǤ���ev(literal_constant) �Ȥ��Ƥ���������
- Fortran �ǡ������ܤγ���ɽ���ϡ����ϥǡ����Ѵ���Ǥ�����˻��Ѥ����ʸ���ޤ��ϡ����ϥǡ����Ѵ����ɽ���˻��Ѥ����ʸ����Τ��ȤǤ���
- ��ĥ��֤��Ѹ�ϡ����ν�λ���� -
�� +
��ޤ�¿��˳�ĥ�Ǥ����֤��̣���ޤ��������ʰ�̣�Ǥϡ����ζ�֤�ޤ���ĥ�¶�֤ν���˴ޤޤ�ޤ���
- ���粼�� (infumum(plural, infima)) �Ȥ��Ƥ���������
- ���ζ�� [empty] �ϡ����С�������ʤ���֤Ǥ������ζ�֤� 2 �Ĥθߤ����Ǥζ�֤��ѽ���Ȥ��ơ�������ȯ�����ޤ������Ȥ��С�[2, 3]��[4, 5] = [empty] �Ȥʤ�ޤ���
- �����
�ϡ����С�������ʤ�����Ǥ������ν���� 2 �Ĥθߤ����Ǥν�����ѽ���Ȥ��Ƽ�����ȯ�����ޤ������Ȥ��С�{2, 3}
{4, 5} =
�Ȥʤ�ޤ���
- �ʳ�Ū����ˡ�ǵ��Ҥ��줿1 �Ĥο��ϡ��������ޤ��ϡ�ͭ�������Ȼؿ����ޤ��ϡ�10 �Τ٤���ǹ�������ޤ���Fortran�� E �Խ����һҤϿ����������ޤ��ϡ�ͭ�������Ȼؿ��������ޤ��ϡ�10 �Τ٤��������ɽ�����ޤ���
- certainly true �ط��黻�ҤȤ��Ƥϡ�{
.CLT.,.CLE.,.CEQ.,.CNE.,.CGE.,.CGT.} ������ޤ���certainly true �ط��黻�Ҥϡ����ڥ��ɶ�֤Τ��٤Ƥ����ǤˤĤ��ơ�����Ȥʤ�ط��� true �Ǥ���С�true �Ȥʤ�ޤ����Ĥޤꡢ���٤Ƥ��ˤĤ��ơ�x .op. y = true �Ǥ���С�[a, b] .Cop. [c, d] = true �Ȥʤ�ޤ���
- ���Ȥ��С�(b < c)�� true �Ǥ���С�[a, b]
.CLT.[c, d] �� true �Ȥʤ�ޤ���
- possibly true �ط��黻�ҤȤ��Ƥϡ�{.
PLT., .PLE., .PEQ., .PNE., .PGE., .PGT.} ������ޤ���possibly true �ط��黻�Ҥϡ����ڥ��ɶ�֤�Ǥ�դ����ǤˤĤ��ơ�����Ȥʤ�ط��� true �Ǥ���С�true �Ȥʤ�ޤ������Ȥ��С�(a < d) �� true �� ����С�[a, b] .PLT. [c, d] if a < d �� true �Ȥʤ�ޤ���
- set �ط��黻�ҤȤ��Ƥϡ�{.
SLT., .SLE., .SEQ., .SNE., .SGE., .SGT.} ������ޤ�������ط��黻�Ҥϡ����ζ�֤ν�λ���ˤĤ��ơ�����Ȥʤ�ط��� true �Ǥ���С�true �Ȥʤ�ޤ������Ȥ��С�(a = c) �� true �Ǥ��ꡢ(b = d)�� true �Ǥ���С�[a, b] .SEQ. [c, d] �� true �Ȥʤ�ޤ���
- ����Ѵ��Ȥϡ����� 10 �ʿ������� 2 �ʿ�����ߤ��Ѵ��ץ������Τ��ȤǤ�������Ѵ��Ͻ����줿�¤Ӥˤ������/���Ϥ���ǹԤ��ޤ���Ʊ������ 2 �ʿ������ƥ�� 10 �ʿ������ƥ�Ǿ��ɽ����ǽ�ʤ櫓�ǤϤ���ޤ��顢��ޤ��ݾڤ��뤿��ˤϡ�����Ѵ����ͭ���δݤ��Ȥʤ�ޤ���
- ��� [a, b] ����
�ζ���ͤǤ����ΤȤ��ޤ���w[a, b] = b - a ����������С�[a, b] �϶�����֤Ǥ��뤳�Ȥˤʤ�ޤ������ [a, b]������������ж����ۤɡ�[a, b] �Ϥ�����Τ� V �˶�����ޤ����Ԥ���ַ�� (sharp interval result)) �⻲�Ȥ��Ƥ���������
- ��֥��르�ꥺ��ϡ���ַ�̤η��˻��Ѥ�����Ϣ�α黻�Ǥ���
- ��ֱ黻�϶�֤�Ȥä����˻��Ѥ���뻻�ѥ����ƥ�Ǥ���
- Fortran �Ǥϡ���ƥ������ζ�ֶ���ͤϥޥ����ɽ����ǽ���ͤǤ���Fortran ɸ��ˤϡ�����Ū�ʶ���ͤ����������郎¸�ߤ��ޤ���
- ���������Ĥ�����������Ǥ����Фο� a
b �ˤ��������줿 [a, b] ={z | a
z
b} �Ǥ���
- �������γ����ͤϡ���������ʸ����ˤ��������줿����Ū���ͤǤ��������� (external value)�Ȥ��Ƥ���������
f95�Ǥϡ�������������Ū�ʶ���ͤϡ�����γ����ͤαԤ�����Ū�ʶ���ͤǤ������Τ��ᡢ���ζ���ͤ�����γ����ͤ�ޤ�Ǥⶹ���ޥ���ɽ����ǽ�ʶ�֤Ȥʤ�ޤ���
- ������ϡ�w([a, b]) = b - a �Τ褦��ɽ����ޤ���
- 1 �Фζ��
�˴ؤ�������黻��
�ϡ�X �� Y��ξ����ޤ�Ǿ��ζ�֤Ǥ� (
�Ȥ�ɽ�����) �����Ȥ��С����Τ褦�ˤʤ�ޤ���
- [2, 3]
[5, 6] = [2, 6].
- ��֥ܥå����ϡ�n �����Υǥ���Ⱥ�ɸ����ʿ�Ԥ��դ����ʿ��ϻ���ΤǤ�����֥ܥå����� n �����ζ�֥٥��ȥ� X = (X1, . . ., Xn)T ��Ȥäƴ��ؤ�ɽ�����뤳�Ȥ��Ǥ��ޤ���
- Fortran �ˤϡ�4 �Ĥ��Ȥ߹��ߤο��ͥǡ������Ȥ��ơ�
INTEGER��REAL��DOUBLE PRECISION REAL��COMPLEX������ޤ������ޥ�ɹԥ��ץ�����-xia�ޤ���-xinterval��Ȥ��ȡ�f95�϶�֤��Ȥ߹��ߤΥǡ������Ȥ���ǧ�����ޤ���
f95�ˤϡ�WID��HULL��MID��INF��SUP��ޤत���������Ȥ߹��ߤ� INTERVAL ��ͭ�δؿ�������ޤ���
- ��̩�������Τ�ȤǤϡ�����ѥ���ϼ�ưŪ�ʷ��Ѵ��ޤ��� KTPV �Ѵ���Ԥ��ޤ����κ���� KTPV �κ��礵�줿��ּ��ϵ�����ޤ���Ǥ�դη��� (�ޤ���) KTPV ���Ѵ�������Ū�˥ץ�����ष�ʤ���Фʤ�ޤ���
- 2 �Ĥμ��Ϥ���餬������Ʊ�� (����礬���٤Ƥβս��Ʊ��) �Ǥ���С���ǽ�Ǥ���
- g ���Ѱ���ˤ��� h ���Ѱ���Τ��٤Ƥ�ñ���� {
} = {x1}
{xn} �ˤĤ��ơ� f({
}) = g(h({
})) �ε���ɤ���ˡ���Ϳ�μ� g �� h ���鿷������ f (������) ��������ޤ���ñ��������ϡ������ؿ��ޤ��ϴط��Τɤ��餫�Ǥ���Ȥ������Ȥ�ż����Ƥ��ޤ���
- ���緿�ζ�ּ��ϰۤʤ뷿�Υǡ������ܤ�ޤߤޤ������Ȥ��С��� [
0.1] +0.2D0�ϡ�[0.1] �� 1 �Ĥζ�֤Ǥ��ꡢ0.2D0��DOUBLE PRECISION������ʤΤǡ����緿�ζ�ּ��Ǥ��������϶���Ʊ�� KTPV = 8 ������ޤ���
- ����⡼�ɤζ�ּ��ϰۤʤ뷿�� KTPV �Υǡ������ܤ�ޤߤޤ������Ȥ��С��� [
0.1] +0.2�Ϻ���⡼�ɼ��Ǥ���[0.1] �� KTPV = 8 ����Ķ������Ǥ�����0.2�� KTPV =4����� REAL ����Ǥ���
- ����Ū�ʥޥ������ 1 �ǽ�����ñ�� (ulp) �ϡ��ޥ���α黻��ǽ��ȤäƼ¹Բ�ǽ�ʺǾ��Υ�����Ȥޤ��ϥǥ�����ȤΤ��ȤǤ������Τ��ᡢ�����줿��֤����� 1 ulp �Ǥ���С�����Ͻ�Ϳ�� KTPV ����ġ���ǽ�ʺǤⶹ��������֤Ȥʤ�ޤ���
- ñ��������/���ϤǤϡ����ۤ˶�֤��ۤ��뤿��ˡ��ǽ�ɽ������Ф� 1�ǽ���ñ�� (uld) �βû��ޤ��ϸ������Ԥ��ޤ���
- ���ν���κǾ���¤ϡ�����ξ�¤ˤ����Ф�ᤤ���Ǥ�������Ͻ��������κ���ο����ޤ��ϡ����������Τ��٤ƤΥ��С������礭���Ǿ��ο��Τ����줫�Ǥ��������� [a, b] �κǾ���� sup([a, b]) �� b �Ǥ���
- ���ν���κ��粼�¤ϡ�����β��¤ˤ����Ф�ᤤ���Ǥ�������ϡ����������κǾ��ο����ޤ��ϡ����������Τ��٤ƤΥ��С����⾮��������ο��Τ����줫�Ǥ��������� [a, b] �κ��粼�� inf([a, b]) �� a �Ǥ���
- �������ἰ�����Τ�ȤǤϡ�����ѥ���ˤ�ꡢ��ưŪ�ʷ��Ѵ��� KTPV �Ѵ����Ԥ��ޤ���Ǥ�դ����֤�ź�����϶�֤˾��ʤ��졢KTPV �� KTPVmax �ؤ����ꤵ��ޤ���
- Fortran �Ǥϡ��������פϡ��ǡ����� (�ޤ���) �黻���������Ƥ��Ƥ����ޤ����Τʤ����¹ԥץ������ΰ���ʬ���̣���ޤ����������ἰ�����Υ������פϡ��ؿ��ȥ��֥롼����θƤӽФ��ˤ�����¤�����ޤ���
- �������ἰ������ �������� (widest-need expression processing: scope)�Ȥ��Ƥ���������
- ��̩������ (strict expression processing) �Ȥ��Ƥ���������
- �������ἰ����(widest-need expression processing) �Ȥ��Ƥ���������
- �������ἰ�����Ǥϡ�����ʸ̮��������� 2 �Ĥ�°���ϡ����η��Ⱥ���KTPV (KTPVmax) �Ǥ���
- ����
�ˤĤ���ɾ�����줿��n �Ĥ��ѿ��μ� f ������ϡ�
��ɽ���졢�ޤ���
�ˤĤ��Ƥϡ����Τ褦���������ޤ���
�ˤĤ��Ƥϡ�
�Ǥ���
- ���٤ƤΥ������� {
}�����
xj �ϡ����� X0 �����ǤǤ���f ������ϡ��嵭������α�¦�ξ�郎�������줿�����٤Ƥβ�ǽ�� f �ν������ν���Ǥ���
is defined for all
.
- ���������ϥ���ѥ���ζ�֥��ݡ��Ȥ���ħ�դ��ޤ������� (narrow width) �϶�֥ǡ������Ѥ��Ȥ߹��ߤΥ���ѥ��饵�ݡ��Ȥˤ������뿷���������ʼ��Ǥ���
- ���������ϡ�����μ��ʡ��ޤ��ϡ�����������°�����ΤǤ���
- ���ष����֤ϥ������ζ�֤Ǥ������ष����֤ϡ�����ͣ������Ǥ����Ǥ���ñ����Ǥ����ۤȤ�ɤξ�硢�����֤� 1 �Ĥ����ȹͤ��뤳�Ȥ��Ǥ��ޤ������Ȥ��С���� [2, 2] �Ͻ��ष�Ƥ��ꡢ��� [2, 3] �Ͻ��ष�Ƥ��ޤ���
- Fortran �Ǥϡ����Ȥ߹��ߥǡ������ϡ��ǡ������μ��� (����) ��������̷��ѥ����� (KTPV) ��Ȥäƥѥ���������ޤ���
f95�ˤϡ�4��8��16 �� 3 �Ĥζ�� KTPV ��¸�ߤ��ޤ����ǥե���Ȥ� KTPV �ϡ�8 �Ǥ���
- �Ǿ���� (supremum(plural, suprema)) �Ȥ��Ƥ���������
- �Ԥ���ַ�̤ϲ�ǽ�ʸ¤궹����������ޤ����Ԥ���ַ�̤ϼ�����ޤ����Ʊ���ˤʤ�ޤ���ͭ�����٤λ��Ѥˤ�����¤��ݤ�����ȡ��Ԥ���ַ�̤ϡ�����������ޤࡢ��ǽ�ʤ�����Ǥⶹ��ͭ�¤ζ�֤Ȥʤ�ޤ���
- ����ʸ�ϡ����η�������� Fortran ʸ�Ǥ���
V =expression- ����ʸ�κ�¦�ϡ��ѿ����������ǡ��ޤ������� V �Ǥ���
- 2 �Ĥθߤ����Ǥζ�֤϶��̤����Ǥ�����ޤ���� [2, 3] �� [4, 5] �ϡ��ߤ����Ǥζ�֤Ǥ���2 �Ĥθߤ����Ǥζ�֤��ѽ���϶��ζ�֤Ȥʤ�ޤ���
- ¿���Ӽ� (MUE) �ϡ����ʤ��Ȥ� 1 �Ĥ���Ω�ѿ���ʣ����и����뼰�Τ��ȤǤ���
- ñ�����Ӽ� (SUE) �ϡ��������dz��ѿ��� 1 �٤�������ȯ�����ʤ����Τ��ȤǤ������Ȥ��С����μ���ñ�����Ӽ��Ǥ�����
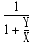
- ���μ��ϡ������ǤϤ���ޤ���
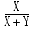
- ñ����֥ǡ����Ѵ��ϡ�
Y�Խ����һҤˤ���ɤ���ñ��ɽ����Ȥä�������֤�ɽ���˻��Ѥ��ޤ���ñ��������/���� (single-number input/output)�Ȥ��Ƥ���������
- ñ��������/���Ϥ϶���Ѥˡ���� [-1, +1]uld �����ۤΤ����˺ǽ�ɽ������ɲä���롢ñ������ɽ������Ѥ��ޤ������դ�ʸ�� uld �ϡ��ǽ���Ǥ�ñ�̤�ɽ��Ƭ���� (Unit in the Last Digit) �Ǥ������Ȥ��С�0.12300 �϶�� 0.12300 + [-1, +1]uld = [0.12299, 0.12301] ��ɽ���ޤ���
- certainly��possibly �ޤ���Ʊ���Ǥʤ�����������̴ط�������Ū�ʴط��ϡ����Ȥ��С�a < b �Τ褦�ˡ��������Ǹ�����ط��Ǥ���
- ����Ū�ʴط��黻�ҤϽ�������ǤǤ�����{<, £, ��, �, >}
- Fortran �Ǥ���������ѿ��ޤ��������ޤߤޤ�������ȥ��ڥ��ɤϴޤ�뤳�Ȥ��Ǥ��ޤ�����
[2,3] + [4,5]��������Ǥ���X���ѿ��Ǥ���С���X + [2,3]��������ǤϤ���ޤ���Y��̾���դ�����Ǥ���С�Y + [2,3]��������Ǥ���
- (��֤���Ω��ǰ�Ȥ��Ƥ�) ���ϡ�1 �Ĥο��Ǥ���N �������֤Ǥ� 1 �Ĥ����ϡ�n �����Υ٥��ȥ� x = (x1, . . . , xn)T ��Ȥä�ɽ����ޤ������Ƚ��ष����֡����뤤�ϡ���֥٥��ȥ��Ʊ����Τȹͤ��뤳�Ȥ��Ǥ��ޤ�����̩�ˤϡ�Ǥ�դζ�֤Ϥ������Ǥ�ʣ�������Ǥ��� 1 �Ĥν���Ǥ���
- Ʃ���ʥǡ�����������Ū�ʶ���ͤι�¤��̤����Τޤޤˤ��ޤ�����֥ǡ������ܤ�Ʃ���Ǥ������Τ��ᡢ�ץ�����ޤ϶�֥ǡ������ܤ�����Ū�˲������̤���ˡ��ɽ������뤳�Ȥ���Ԥ��뤳�Ȥ��Ǥ��ޤ����Ȥ߹��ߤδؿ�
INF��SUP�϶�֤ι������ǤؤΥ������������ޤ������Ȥ�Ǥ�դ�ͭ���ʶ�֤��ۤ���ˤϡ�INTERVAL�����Ҥ�Ȥ����Ȥ��Ǥ��ޤ���
- ̾���դ������
PARAMETERʸ�������������������ޤ���̾���դ�������ͤ�ʸ̮�˰�¸���ʤ��Τǡ�PARAMETER����ǤΥǡ������ܤΤ��Ŭ�ڤ�̾���ϡ����ɤ�������ѿ��פǤ���
- ȿ����Ū�ʴط��� true �Ȥʤꤨ�ʤ����Ȥ���ˤĤ��Ƥ��ĽҤǤ�����̴ط� �� �ϡ�Fortran �Ǥ�ͣ���ȿ����Ū�ʴط��Ǥ���
- Fortran ��
.NE.�� /= �黻�Ҥ�ȿ����Ū�ʴط���������Ƥ��ޤ���certainly��possible����֥��ڥ����Ѥν���С������ϡ����줾�졢.CNE.��.PNE.��.SNE.��ɽ����ޤ���
- 1 �Ĥζ�֤κ�¦�ν�λ���ϡ����κ��粼�¤ޤ��ϲ��¤�Ʊ���Ǥ���
- �������ἰ�����Τ�ȤǤζ�����������Ū�ʶ���ͤϡ�KTPVmax ��Ʊ�� KTPV ����ıԤ���֤ʤΤ�ʸ̮��¸�Ȥʤ�ޤ�����������ǡ������� [a, b] �ˤĤ��Ƥ�Ǥ�դζ���ͤ�Ȥ����Ȥ��Ǥ��ޤ���
- [a,b]
ev(
[a,b]),- �����Ǥϡ�ev([a,b]) �϶����� [a,b] �γ����ͤ�ɽ���ޤ�����ޤΰ�ȿ���ʤ���С�Ǥ�դ�����Ū�ʶ���ͤ����뤳�Ȥ�������ޤ������Ȥ��С�����Ū�ʶ���� [0.1_4]��[0.1_8] �� [0.1_16] �ϡ����٤Ƥ������� ev(0.1) = 1/10 ����������Τ��ᡢ��ޤ�����˰�ȿ���ޤ��������ἰ�����Τ�ȤǤϡ�KTPVmax ��Ʊ�� KTPV ���������Ū�ʶ���ͤ����Ѥ��ޤ���
- �ĺ���֤Ϥ��ν�λ����ޤߤޤ����ĺ���֤��Ľ��� (closed set) �Ǥ���[2, 3] = {z | 2 £ z £ 3}�Ǥ����֤Ϥ��ν�λ�����ޤޤ��Τ��Ĥ����Ƥ��ޤ������ (2, 3) = {z | 2 < z < 3} �Ǥ����֤Ϥ��ν�λ�����ޤޤ�ʤ��Τǡ������Ƥ��ޤ���
f95�Ǽ������줿��ֱ黻�ϡ��ĺ���֤������갷���ޤ���
- �ĺ����إ����ƥ������Ǥϡ�̤����α黻�ҥ��ڥ��ɤ��Ȥ߹�碌��¸�ߤ��ƤϤ����ޤ����ĺ������ƥ�����Ǥ˴ؤ��뤹�٤Ƥ�����Ѥ߱黻�Ϥ��Υ����ƥ�����Ǥ��������ʤ���Фʤ�ޤ��¿������ƥ�ϡ������ˤ����������Υ����ƥ��̤����ʤΤǡ��Ĥ����Ƥ��ޤ���
- �Ľ���Ͻ��������Τ��٤Ƥν����� (limit point �ޤ��� accumulation point) ��ޤߤޤ����Ĥޤꡢ��Ϳ�ν��� S �ȥ�������
�ˤĤ��ơ�S ������ϡ�
�Ȥʤ�ޤ��������Ǥϡ�
�ϥ������� {sj} �ν�������ɽ���ޤ���
- �¿��ν���ϡ�-
�� +
��ޤޤʤ��Τǡ����������� {z | -
< z < +
} �Ǥ�����ĥ�¿��ν���
���Ĥ��Ƥ��ޤ���
- ������������Ľ�Ϳ�μ� f��g��h �ˤĤ��ơ�
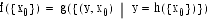
- ������������ϡ����Τ��Ȥ��ޤ���
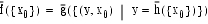
- �� x0 �Ǥ�
������ϡ����λؿ�������Ǥ���
��
��Ʊ���Ǥ���
- ����� (interval hull) �Ȥ��Ƥ���������
- �� h ������� cset(h, {x}) �ϡ�h ��Ǥ�դι��� f({x}) = g(h({x}), {x}) �ι������ǤȤ��ƻȤ���ȡ���ޤ�����˰�ȿ���ʤ��Ǿ��ν���Ȥʤ�ޤ���
- For h(x, y) = x ÷ y �ˤĤ��Ƥϡ�
- cset(h, {(+
, +
)}) = [0, +
] �Ȥʤ�ޤ���
- cset(expression, set) �⻲�Ȥ��Ƥ���������
- �����Τɤ���ʬ��Ʊ���Ǥ����硢2 �Ĥμ���������Ʊ�ͤǤ���
- eval(f, {x}) �����ġ��ι������Ǥ������Ȥäơ��黻���ؿ������뤤�ϡ��ط����ͤΤ�����Ǥ��äƤⲼ�̼����ͤ�����롢�� f �Υ����ɥꥹ�Ȥ�ɾ����ɽ����ΤȤ��ޤ������ξ�硢f ���ؿ��Ǥ��äƤ�ط��Ǥ��äƤ⡢��f({x}) = f({x1}
{xn}) ��Ϳ������ȡ����٤Ƥ�
�ˤĤ��ơ�cset(f, {x0})
eval(f, {x0}) �Ȥʤ�ޤ���
- n �Ĥ��ѿ���Ǥ�դμ� f({x}) = f({x1}
{xn}) ���� x0 ��Ϳ������ȡ��� x0�Ǥ� f ������ϡ�cset(f, {x0}) = f({x0}) �Ȥʤ�ޤ���
- ��ޤμ��Ԥϡ���ޤ�������������ʤ����ԤǤ������Ȥ��С�[1]/[0] �� [empty] �Ǥ������������ȡ���ޤμ��ԤȤʤ�ޤ�������ϡ�
�Ǥʤ� Y �Ǥ��� X=[0]�� Y �ˤĤ��ơ����Τ褦�ʶ�ּ������ꤹ��г�ǧ���뤳�Ȥ��Ǥ��ޤ���
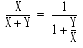
- �ǽ�μ��������� [0] �Ǥ�����������[1]/[0] �� [empty] �Ǥ������������ȡ�2 ���ܤμ���ޤ� [empty] �Ȥʤ�ޤ�������ϡ���ޤμ��ԤǤ���
- ���ष����� [x] �Ǥμ� f �ζ�֤�ɾ�� f([x]) �˴ؤ�����ޤ�����ϡ����Τ褦�ˤʤ�ޤ���
- f([x])
cset(f,{x}),
- �����Ǥϡ�cset(f,{x}) �� f([x]) ���ޤޤʤ���Фʤ�ʤ����٤Ƥβ�ǽ���ͤ�������ɽ���ޤ��������ϡ�(x ÷ y, {(1, 0)}) = {-
, +
}�Ǥ����顢[1] / [0] = hull({-
, +
}) = [-
, +
]�Ȥʤ�ޤ�������� (containment set)�⻲�Ȥ��Ƥ���������
- �Ǿ���� (supremum(plural, suprema)) �Ȥ��Ƥ���������
- ͭ���δݤ�����̤ʸ�������Ĵݤ�Ǥ�����ֱ黻��ʸ̮�Ǥϡ��ݤ��ڤ�夲�� +
�����Ρ��ݤ��ڤ겼���� -
�����θ���������ޤ���ͭ���δݤ��������Ȣ��ˤ�국�沽����ޤ������Τ��ᡢ���� 5 ��λ��Ѥ�Ȥ���硢�� 2.00001 = 2.0001 �Τ褦�ˤʤ�ޤ���ͭ���δݤ�ϡ�����ԥ塼�������ޤ�����˰�ȿ���뤳�Ȥ��ʤ��褦����ֻ��Ѥμ����ǻ��Ѥ��ޤ���
- �ɤ�������ѿ���ɸ�� Fortran ������Ѥߤι�����ǰ�ǤϤ���ޤ�������������Ǥ��ɤ�������ѿ��ϰ��ٽ�������줿����ѹ��Ǥ��ʤ��ʤ�ޤ�����֥��ݡ��ȤΤʤ�ɸ�� Fortran �Ǥϡ�̾���դ�������ɤ�������ѿ�����̤���ɬ�פ�����ޤ����������������ἰ����������γ����ͤ�Ȥ��Τǡ��ɤ�������ѿ���̾���դ��������̤��ʤ���Фʤ�ޤ���f95 �μ����Ǥϡ�
PARAMETER�������ǽ��������뵭��̾���ɤ�������ѿ��Ȥʤ�ޤ���
f95�Ǥϡ���֥�ƥ������ϡ�����γ����ͤ�������뤿��˻��Ѥ����ʸ����Ǥ���
f95�Ǥϡ���ƥ������γ����ͤ������ʸ����ˤ��������줿���ؾ���ͤǤ��������� (external value)�⻲�Ȥ��Ƥ���������
f95�Ǥϡ�����Ū�ʥ�ƥ�����������Ū����ͤϡ�����γ����ͤ�ޤ�Ԥ��ޥ���ɽ����ǽ�ʶ�֤Ǥ���
- IEEE754 ��ư������ɸ��Ǥϡ������ˤ������Τ褦��̤����α黻��¹Ԥ��褦�Ȥ���ȡ��㳰��ȯ�����ޤ���
- 2 �Ĥ��ͤ�ޤࡢ2 �Ĥ��ʹ֤ο���Ϣ�뽸�� a £ b �ϡ�a �� b ��ޤ� a��b �֤Τ��٤Ƥ��ͤ�ޤߤޤ���
|
���ޥ����������ƥॺ������� Copyright information. All rights reserved. |
�ۡ��� | �ܼ� | ���ڡ����� | ���ڡ����� | ���� |