| Fortran 95 区間演算プログラミングリファレンス |
第 1 章
f95で区間演算を使用するには
f95 INTERVAL型と区間演算サポート区間演算は、数の区間を使って計算を行うためのシステムです。区間演算は常に可能なすべての結果値の組み合わせを含む区間を生成するため、区間アルゴリズムはきわめて困難な計算を実現するように開発されました。区間アプリケーションのより詳細な情報については、
READMEの区間演算を参照してください。区間演算の誕生以来、狭幅区間の結果を生成する区間アルゴリズムが開発され、区間言語をサポートするための構文と意味論が設計されてきました。しかし、市場で利用でき、サポートを受けられる区間コンパイラについてはあまり改善されていません。1 つの例 (M77 Minnesota FORTRAN 1977 標準バージョン第 1 版) を除いて、区間システムは、これまで、プリプロセッサ、C++ クラス、あるいは、Fortran 90 のモジュールを基につくられています。
f95で区間データのサポートをコンパイラに組み込んだ目的は次のとおりです。Sun WorkShop 6 の
f95リリースでの区間サポートは、大幅に拡張されています。
f95区間サポートの目的:実装品質
f95における組み込みの区間サポートの目的は、プログラム開発者に、次のような機能を提供することで、商業ベースの区間解決ライブラリとアプリケーションの開発を活性化することです。サポートと機能は、実装品質の構成要素です。このマニュアルでは、全体を通してさまざまな実装品質が説明されています。お客様からの改善提案も受け付けております。
高品質の区間コード
正しい区間サポートコンパイラは、任意の区間式の評価の結果として、可能なすべての結果値の組み合わせを含む区間を生成しなければなりません。可能なすべての結果値の組み合わせを含むという要件は、区間演算の包含の制約と呼ばれます。この包含の制約を満たせない失敗は内部的なエラーです。区間の包含の制約を満たせない隠れた(警告や文書を伴わない) エラーは、任意の区間計算システムで致命的なエラーとなります。この 1 つの制約を満たすことで、区間は新しい計算品質を提供します。
包含の制約が満たされれば、実装品質は、実行時間と区間幅の軸を持つ二次元の平面上の 1 つの点の位置で決まります。両軸上は小さい値ほど良いことになります。実行時間と区間幅間の関係はアプリケーションに依存しますが、実行時間と区間幅は、区間システム品質の明確な尺度となります。区間幅と実行時間は常に実行時に入手して利用できますから、区間アルゴリズムと実装システムの両方の正確性の測定は速度の測定と同様、難しいことではありません。
Sun WorkShop 6 のパフォーマンスプロファイリングツールは区間プログラムの調整に使用できます。しかし、
f95には、アルゴリズムが不要に区間幅を増大する可能性のある場所を特定するための区間固有のツールはありません。「コード開発ツール」で解説しているように、区間のdbxと大域的なプログラム検査 (GPC) のサポートが提供されています。区間固有のコード開発とデバッグツールの追加により、優れた実装品質が得られます。狭幅区間の生成
すべての言語やコンパイラの実装品質の基準となる項目、たとえば速度や使いやすさは区間用のツールにも適用されます。
更に、有効な区間実装システムは、常に包含の制約を満たす一方で計算区間の幅を最小化するという実装品質の基準もあります。
区間の幅が狭いほど、それは「鋭い」と表現されます。所与の浮動小数点精度について、区間幅が狭いほど、生成される区間は鋭くなります。
f95コンパイラにより生成される区間の幅については、次のことがあてはまります。迅速に実行できる区間コード
コンパイラの最適化とハードウェアの命令サポートの提供により、区間演算が対応する
REAL浮動小数点よりも著しく低速になることはありません。f95では、組み込みの区間演算子と算術関数の速度について、次のことがあてはまります。
- 算術演算は適度に高速です。
- デフォルトの区間算術関数の速度は、一般的に、対応する
DOUBLE PRECISIONの 2 倍未満です。KIND=4であれば、組み込みの区間算術関数の速度は調整されません (対応するKIND=8関数とは異なる)。このリリースでは、KIND=16の数学関数は提供されません。しかし、その他のKIND=16区間関数はサポートされます。- 次の組み込み区間配列関数では、パフォーマンスが最適化されています。
使いやすい開発環境
Fortran の組み込みの区間データ型は区間コードの開発、テスト、実行に役立ちます。区間コードを分かりやすくする (読み書きしやすくする) ために、区間構文と意味論が Fortran に追加されています。最終的には、これらの機能がユーザーに受け入れられれば、将来の Fortran 規格に取り入れられることになります。
区間を Fortran への組み込みデータ型として導入することで、Fortran の適用可能なすべての構文と意味論がすぐに利用できるようになります。Sun WorkShop 6 の
f95は、以下のような Fortran 区間機能の拡張を含んでいます。
INTERVALデータ型- 区間算術演算と組み込みの数学関数は閉じた数学システムです。(つまり、ゼロによる除算やその他のゼロや無限大などの不定形式を含む、任意の可能な演算子オペランドの組み合わせに対して有効な結果を生成します。)
- 区間関係演算子の3つの種類
.IX.(積集合) と.IH.(区間包) のような、組み込みの区間固有の演算子INF、SUP、WIDなどの区間固有の関数- 単数の入出力を含む区間の入出力
- 式の文脈依存の区間定数
- 混合モード区間式処理
これらの機能とその他の組み込み機能に関する例とより詳細な情報については、コード例 1-11 からコード例 1-14 までの例と「組み込み区間関数」を参照してください。
第 2 章ではこれらの関数とその他の区間機能を解説しています。
f95区間コードの記述この節の例は、初めて区間に接するプログラマが基本を理解し、有用な区間コードをすぐに記述できるような内容となっています。これらの例を基にして変更したり実際に使ってみることをおすすめします。
本書のすべてのコード例は、次のディレクトリに含まれています。
/opt/SUNWspro/examples/intervalmath/docExamples各例の名前は「
cen-m.f95」となっていますが、n は例の現れる章を、mは例の番号を表しています。また、次のディレクトリには、追加の区間例が含まれています。/opt/SUNWspro/examples/intervalmath/generalコマンド行オプション
f95コマンド行に以下のコマンド行マクロを含めると、組み込みのINTERVALデータ型を認識し、区間式の処理を制御します。組み込みの
INTERVALデータ型がコンパイラにより認識されるためには、f95のコマンド行で、-xiaまたは-xintervalを入力する必要があります。区間と関連するすべてのコマンド行オプションについては、「区間のコマンド行オプション」で解説しています。最大幅要求式と厳密式の処理については、「区間演算式」で解説しています。
コード例 1-1では、
f95の区間サポートを使用した最も簡単なコマンド行呼び出しを示しています。Hello Interval World
別途明示的な解説がない限り、すべてのコード例は、
-xiaコマンド行オプションを使ってコンパイルできます。-xiaコマンド行オプションはf95に対する区間拡張を使用するために必要です。コード例 1-1 は、区間用の「Hello world」です。
コード例 1-1 Hello Interval World
cat ce1-1.f95PRINT *, "[2, 3] + [4, 5] = ", [2, 3] + [4, 5] ! 1 行目ENDmath%f95 -xia ce1-1.f95math%a.out[2, 3] + [4, 5] = [6.0,8.0]コード例 1-1 では、並びによる出力を用いて、区間 [2, 3] と [4, 5] の名前付き合計を表示しています。
区間の宣言と初期化
区間宣言文は、
REAL、INTEGER、COMPLEXの宣言がそれぞれのデータ型に対して行うのと同じ機能を区間データ項目に対して実現します。区間のデフォルト種別型パラメータ値 (KTPV) は、INTEGERのデフォルトの KTPV の 2 倍です。これにより、任意のデフォルトINTEGERを縮退したデフォルトの区間を使って正確に表現できるようになります。より詳細な情報については、「デフォルトの種別型パラメータ値 (KTPV)」を参照してください。コード例 1-2 は、区間変数と初期化を使用して、コード例 1-1 と同じことを実現しています。
コード例 1-2 区間変数を使用した Hello Interval World
cat ce1-2.f95INTERVAL :: X = [2, 3], Y = [4, 5] ! Line 1PRINT *, "[2, 3] + [4, 5] = ", X+Y ! Line 2ENDmath%f95 -xia ce1-2.f95math%a.out[2, 3] + [4, 5] = [6.0,8.0]1 行目では、変数 X と Y をデフォルト型の区間変数と宣言し、それぞれを [2, 3] と [4, 5] に初期化しています。第 2 行目では、並びによる出力を使って、名前付き区間
XとYの合計を表示しています。区間の入出力
区間の読み取りと書き出し用には完全なサポートが提供されます。区間と
COMPLEXデータ項目の読み取りと書き出しは類似しています。区間は囲み記号として丸括弧でなく角括弧を用います。区間データの読み取りと対話形式の入力は冗長になるので単数区間形式が導入されています。単数変換とは、角括弧に含まれない任意の数が、最後の表示桁に 1 単位を加算、減算して下限と上限が構築される 1 つの区間として翻訳されることです。
- 2.345 = [2.344, 2.346],
- 2.34500 = [2.34499, 2.34501],
- 23 = [22, 24].
- [2.34499, 2.34501] = 2.34500 + [-1, +1]uld
ここでは、[-1, +1]uld は、先行する数の最後の桁に区間 [-1, +1] が追加されることを意味します。添字 uld は、「最終桁の単位」(unit in the last digit) のニーモニックです。
縮退した区間を表すには、単一の数を角括弧で囲むことができます。たとえば次のように表されます。
- [2.345] = [2.345, 2.345] = 2.345000000000.....
この変換は、入力と Fortran コードの縮退したリテラルな区間定数の両方に用います。このため、入力値を示す型
[0.1]は、0.1 をマシンが表現できない場合でも、1 つの正確な十進小数となります。たとえば、プログラムに入力中の
[0.1,0.1] = [0.1]は、点 0.1 を表しますが、単数入出力用法での0.1は、次のような区間を表します。
- 0.1 + [-1, +1]uld = [0, 0.2].
f95では、入力変換処理は入力小数値を含む 1 つの鋭い区間を構築します。その値がマシンで表現できる場合は、内部的なマシン近似値は縮退しています。その値がマシンで表現できない場合は、1-ulp (仮数部の最終位置の単位) の幅を持つ区間が構築されます。
注 - uld と ulp は異なります。uld は最終表示桁に対する 1 単位の加減算を行うために、暗黙に、単数入出力形式を用いて区間を構築することを意味します。ulpは内部的なマシン数に与えることのできる最小の可能なインクリメントまたはデクリメントです。
区間データ項目を読み取ったり、印刷する最も簡単な方法は、並びによる入出力を使うことです。
コード例 1-3 は、ユーザーが並びによる
READと
注意 -区間の包含の制約は、入力中と出力中の両方で、丸めを使うことを必要としています。単数入力の直後で単数が出力されると、小数桁精度が失われることになります。実際に、入力値がマシン表現できない場合、入力区間幅は最大で 1-ulp だけ増えます。「単数の入出力」と コード例 1-6 を参照してください。
コード例 1-3 区間の入出力
単数の入出力
区間出力を読み取る際には、区間の最大下限と最小上限を比較して一致する桁数を数えることは手間のかかる作業の一つです。たとえば、コード例 1-4 とコード例 1-5 は、いろいろな幅を持つランダムな区間データを生成します。
注 - コード例 1-4 とコード例 1-5 では、プログラムの出力だけを示しています。この出力を生成するコードは、/opt/SUNWspro/examples/intervalmath/docExamplesディレクトリの例に含まれています。
コード例 1-4 [inf,sup] 区間出力
cat ce1-4.f95f95 -xia ce1-4.f95a.out5,4,05,8,05,16,0コード例 1-4 の出力の読みやすさをコード例 1-5 のものと比較してみてください。
コード例 1-5 単数出力
a.out5,4,15,8,15,16,1単数表示形式では、後続のゼロが意味を持ちます。より詳細な情報については、「入力と出力」を参照してください。
区間は、伝統的な [inf, sup] 表示形式を使って、常に入力、表示することができます。また、角括弧で囲まれた単数は点を表します。たとえば、
コード例 1-6 内部データ変換を伴う文字入力[0.1]の入力は、1/10 に翻訳されます。包含を保証するために、丸めによる方法を使って、1/10 の数を含むことがわかっている区間の近似値が構築されます。
cat ce1-6.f951 FORMAT(" X = ? ")f95 -xia ce1-6.f95a.out1.371.444コード例 1-6 注記:
- 角括弧内部の単数は縮退した区間を表します。
- 単数入力でマシンが表現できない数が読み取られると、10 進数から 2 進数への変換 (基数変換) が行われ、包含の制約によりその数の区間幅が 1-ulp (小数部分の最後の位置の単位) だけ強制的に増やされます。この結果を単数出力を用いて表示すると小数桁の精度が失われた形で現れます。そうではなく、単数区間入力を正確に反映するためには、コード例 1-6 が示しているように、文字入力は内部
READ文のデータ変換と併用されなければなりません。
注 -f95は、空の区間をサポートします。空の区間は、"[empty]"と入力できます。「外部表現」の記述と コード例 2-37 で示しているように、無限区間の終了点もサポートしています。
区間の文と式
f95コンパイラには以下のような区間固有の文、式、拡張が含まれます。
- 表 1-1 で示している、
INTERVALデータ型、関連命令、文がサポートされています。- 実引数を受け入れるすべての組み込み関数は、対応する区間バージョンを持ちます。(整数については当てはまらない既知のエラーが存在します。「整数オーバーフロー」を参照してください。)
- 区間固有の関係演算子や「集合」論関数を含む、多くの組み込みの区間固有の関数と演算子が追加されています。組み込み区間関数と区間演算子の完全なリストについては、「組み込み関数」と 「数学関数」を参照してください。
デフォルトの種別型パラメータ値 (KTPV)
表 1-1 区間固有の文と式
INTERVALINTERVAL(4)INTERVAL(8)INTERVAL(16)INTERVAL型宣言KIND=4のINTERVALKIND=8のINTERVALKIND=16のINTERVAL[a,b](1)INTERVAL文字定数:[a,b][a](2)[a,a]INTERVAL APARAMETER A=[c,d]
名前付き定数:AV =expr (3)FORMAT(E,EN,ES,F,G,VE,VF,VG,VEN,VES,Y)(4)E,EN,ES,F,G,VE,VF,VG,VEN,VES,Y編集記述子(1) 文字 a と b は、 0.1、0.2のような小数文字定数可変部分が入ります。 (2) 角括弧内部の単一の小数定数は縮退した区間定数を表します。入出力でも同様です。 (3) expr が、INTERVAL型の項目を含むかどうかにかかわらず、任意の Fortran 算術式を表すものとします。V=expr の代入文は式 expr を評価しその結果の値を V に代入します。-xia=strictコマンド行オプションのもとでは、混合モードの区間式は使用できません。-xia、または、-xia=widestneedオプションのもとでは、混合モード式は最大幅要求式処理を使って正しく評価されます。最大幅要求のもとでは、式評価の前に、すべての整数と浮動小数点データ項目は、Vを含む式の中で使われている最大の KTPV を持つ区間を含むよう昇格されます。詳細については、「値の代入」を参照してください。 (4) 区間の入出力サポートは、柔軟性、可読性、開発の容易性を提供するよう設計されています。最も重要な新しい編集記述子はYですが、この記述子は単数区間形式を使って区間を読み、表示するために用いられます。区間を処理できるすべての記述子の完全な説明については、「入力と出力」を参照してください。
f95では、デフォルトのINTEGERKTPVは、KIND(0)= 4 です。縮退したデフォルトの区間を使って任意のデフォルトINTEGERを表すためには、デフォルトの区間KTPVであるKIND([0])が、2*KIND(0)= 8 である必要があります。これは次の理由によります。
- 区間は、CDC や Cray のマシンで実行されてきたような数値演算に特化した計算の実行によく用いられます。
- 単一の算術式の評価では、累積した丸めエラー、依存、取り消しのために、区間の幅は必ず増えます。精度を上げることにより、累積した丸めエラーの影響を軽減させることができます。
値の代入
V=expr区間の代入文は、可変部分 expr で表される区間式の値を、区間変数、配列要素、あるいは、配列としての
Vに代入します。構文は次のとおりです。V = exprV は、
INTERVAL型を持たなければならず、また、expr は任意の非COMPLEXの数式を表します。最大幅要求式処理のもとでは、式 expr は、区間式である必要はありません。厳密式処理のもとでは、expr は、Vと同じKTPVを使った区間式でなければなりません。混合型式の評価
混合型の区間式を有効に使用することは、明確な (理解しやすい) 算術式の記述に役立つので、重要で使いやすい機能です。
混合型の区間式は、区間コードの記述と読みを
REALコードと同じように使いやすくするためにサポートされています。区間の包含の制約は、最大幅要求または厳密のいずれかの式処理を用いた混合モード式で満たされます。最大幅要求式処理と厳密式処理
区間定数の幅が、「区間演算式」で解説しているように、式の文脈により動的に定義されている場合には、狭幅区間結果の計算が役立ちます。コード例 1-7 で示しているように、KTPV 混合式の中では、動的に増加する区間変数の KTPV が区間式結果の幅を減少させることもあります。
コード例 1-7 最大幅要求を用いた混合精度
math%cat ce1-7.f95INTERVAL(4) :: X = [1, 2], Y = [3, 4]INTERVAL :: Z1, Z2!最大幅要求コードZ1 = X*Y ! 3 行目
!同等の厳密コードZ2 = INTERVAL(X, KIND=8)*INTERVAL(Y, KIND=8) ! 4 行目IF (Z1 .SEQ. Z2) PRINT *, 'Check.'ENDmath%f95 -xia ce1-7.f95math%a.outCheck.3 行目では、KTPVmax =
KIND(Z)=8となります。この値は、積の計算前に、XとYの KTPV を 8 へと昇格させ、結果をZ1に格納するのに使用されます。これらの手順は、4 行目の同等の厳密コードの中で明示的に示されています。
文を走査して最大 KTPV を決定し必要な昇格を実行するプロセスは、最大幅要求式処理とよばれます。「区間演算式」を参照してください。
区間構成子の構文と意味論については、「組み込み区間演算子の拡張」を参照してください。
(型と KTPV の) 混合モード式
KTPV とデータ型と共に、最大幅要求の原則が用いられると、(型と KTPV の) 混合モード区間式が安全かつ予測的に評価できるようになります。たとえば、コード例 1-8 では、
コード例 1-8 最大幅要求を用いた型混合XとYは区間変数なので、3 行目のY1の式は 1 つの区間式です。
cat ce1-8.f95INTERVAL(16) :: X = [0.1, 0.3]INTERVAL(4) :: Y1, Y2! 最大幅要求コードY1 = X + 0.1 ! 3 行目! 同等の厳密コードY2 = INTERVAL(X + [0.1_16], KIND=4) ! 4 行目IF (Y1 == Y2) PRINT *, "Check."ENDmath%f95 -xia ce1-8.f95math%a.outCheck.包含を保証するためには、定数 0.1 に対する実近似値の代わりに内部的な区間が使用されなければなりません。しかし、
KIND(X)=16なので、KTPVmax = 16 となります。このため、Xの更新には、正確な値 1/10 を含む鋭い KTPV = 16 区間である区間定数 [0.1_16] が使用されます。最後に、この結果が区間を含む KTPV = 4 へと変換され、Yに代入されます。4 行目は同等の厳密コードを含んでいます。厳密式処理のもとでは、混合型または混合 KTPV の式はどちらも許可されません。1. 左側を含む文全体を走査して、任意の区間データ項目を求めます。INTERVAL 型の定数、変数、または、組み込み関数があると、式の型は INTERVAL になります。
2. 区間式を走査して、各INTERVAL、REAL、INTEGER、定数、または変数の KTPV にもとづき、KTPVmax を求めます。
注 - 整数は 2 倍の KTPV を持つ区間に変換されるので、すべての整数値は正確に表現できます。
3. すべての変数と定数を KTPVmaxを持つ区間に昇格させます。4. 式を評価します。5. 左側の KTPV に一致させる必要があれば、結果をより低い KTPV へと変換します。6. 生成された値を左側に代入します。これらの手順は、混合モードの区間式処理が包含の制約を満たし、効果的に合理的な狭い区間結果を生成することを保証します。
最大幅要求式処理を使った混合モードの区間式の評価は、
-xiaコマンド行フラグを使ったデフォルトでサポートされます。-xia=strictを使うと、区間への任意の自動的な型変換と任意の区間変数の自動的な KTPV の増加を行いません。厳密モードでは、すべての区間型と精度の変換が明示的にコード化されなければなりません。演算式
区間データ項目を含む算術式の記述は、簡単で直接的です。区間文字定数と組み込みの区間固有の関数を除けば、区間式は
コード例 1-9 簡単な区間式の例REAL算術式のように見えます。特に、最大幅要求式処理では、REALとINTEGER変数と文字定数は、コード例 1-9 で示しているように、区間式の中のどこででも自由に使用することができます。
cat ce1-9.f95INTEGER :: N = 3REAL :: A = 5.0INTERVAL :: XX = 0.1*A/N ! 5 行目PRINT *, "0.1*A/N = ", XENDmath%f95 -xia ce1-9.f95math%a.out0.1*A/N = [0.16666666666666662,0.16666666666666672]5 行目で代入が行われる変数 X は 1 つの区間ですから、式 0.1 * A/N の評価の前に、次の手順が実行されます。
1. 文字定数 0.1 は、縮退した区間[0.1]を含むデフォルトの区間変数へと変換されます。規格に沿った区間システムの実装での要件ではありませんが、Sun WorkShop 6 の
f95は鋭いデータ変換を実行します。たとえば、区間の近似値 [0.1] は 1-ulp の幅となります。2.REAL変数Aは、縮退した区間[5]に変換されます。3.INTEGER変数Nは、縮退した区間[3]に変換されます。式 [0.1]×[5]/[3] は、区間演算を使用して評価されます。上記手順は最大幅要求式処理の一部であり、これは、混合モードの区間式の評価時の包含の制約を満たすために必要です。「混合型式の評価」を参照してください。
区間代入文は、代入先の変数が区間変数、配列要素または配列でなければならないという 1 つの要件を満たさなければなりません。最大幅要求処理モードに関する詳細情報については、「混合モードの区間式」を参照してください。
Sun WorkShop 6 の
f95で実装された区間システムは閉鎖型ですから、任意の区間式が有効な区間結果の生成に失敗すれば、コンパイラエラーとして表示されます。疑わしいエラーの表示方法については、「コード開発ツール」を、既知のエラーの一覧については、「既知の内部的なエラー」をそれぞれ参照してください。
注 - 算術的に同等の区間式が常に同じ幅を持つ区間を生成するわけではありません。また、単一の区間式を評価するだけでは鋭い結果を計算できないことがよくあります。一般的に、区間の結果としての幅は、区間引数の値と式の形式に依存します。
区間の順位関係
区間の順位付けは点の順位付けよりも複雑です。2 が 3 よりも小さいことをテストするのはあいまいなことではありません。区間を使用すると、区間
[2,3]は区間[4,5]よりも小さいことになりますが、区間[2,3]と[3,4]の場合はどのように表現すべきなのでしょう?区間関係演算子としては、以下の 3 つの異なるクラスが実装されています。
断定的な関係が true となるためには、オペランド区間のすべての要素がその関係を満たさなければなりません。オペランド区間の任意の要素によりその関係が満たされると、可能性のある関係は true となります。集合の関係は、区間を集合として取り扱います。区間関係演算子のこれらの 3 つのクラスは、両方のオペランド区間が共に縮退すると、点に関する通常の関係演算子に収束します。
3 つの演算子クラスを区別するために、通常の 2 文字で表す Fortran のニーモニックには、
C、P、または、S 文字の接頭辞を付けます。f95では、集合演算子.SEQ.と.SNE.は、点型のデフォルト (.EQ.または==、と、.NE.または/=) がサポートされる唯一の演算子となっています。その他のすべてのケースでは、次の例のように、関係演算子クラスが明示的に識別されなければなりません。すべての区間演算子の構文と意味論については、「組み込み演算子」を参照してください。
次のプログラムは、「集合の関係」での等式テストを示しています。
コード例 1-10 集合等式テスト
cat ce1-10.f95INTERVAL :: X = [2, 3], Y = [4, 5] ! 1 行目IF(X+Y .SEQ. [6, 8]) PRINT *, "Check." ! 2 行目ENDmath%f95 -xia ce1-10.f95math%a.outCheck.2 行目では、集合の関係の等式テストを使って、
X+Yが区間 [6, 8] に等しいことを検証しています。IF(X+Y == [6, 8]) PRINT *, "Check." ! 2 行目区間固有の関係演算子の結果を試してみる場合は、コード例 1-11 と コード例 1-12 を使ってください。
コード例 1-11 区間関係演算子
cat ce1-11.f95f95 -xia ce1-11.f95a.out[2] [3]2 3コード例 1-12 は、表 1-2 に掲載した区間固有の演算子用法を例示しています。
表 1-2 区間固有の演算子
区間包 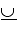
積集合 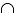
素 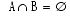
要素 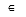
内部 「内部:(X .INT. Y)KAKKOEを参照してください。 真部分集合 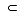
真超集合 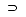
部分集合 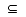
超集合 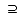
コード例 1-12 集合演算子
cat ce1-12.f951 FORMAT(" X, Y = ? ")f95 -xia ce1-12.f95a.out[1] [2][1,2][1,3]組み込みの区間固有の関数
組み込みの区間固有の関数としてさまざまなものが提供されています。「組み込み関数」を参照してください。コード例 1-13 を使うと、組み込みの区間固有の関数の動作を調べることができます。
コード例 1-13 組み込みの区間固有の関数
cat ce1-13.f951 FORMAT(" X = ?")f95 -xia ce1-13.f95a.out[1.23456,1.234567890][1,10]標準組み込み関数の区間バージョン
Fortran の
コード例 1-14 標準組み込み関数の区間バージョンREAL引数を受け入れるすべての組み込み関数は、区間バージョンを持っています。「組み込み関数」を参照してください。コード例 1-14 を使用すると、いくつかの組み込み関数の動作を調べることができます。
cat ce1-14.f951 FORMAT(" X = ?")f95 -xia ce1-14.f95a.out[1.1,1.2][-0.5,0.5]コード開発ツール
区間コード開発に関する情報はオンラインで利用できます。区間の Web サイト一覧とその他のオンラインのリソースについては、区間演算の
READMEを参照してください。疑わしい区間エラーを報告される場合は、次の宛先に電子メールをお送りください。
sun-dp-comments@Sun.com
WORKSHOP "6.0mm/dd/yy" Intervalデバッグのサポート
Sun Workshop 6 では、区間データ型は dbx により次に示す範囲でサポートされます。
- 各区間変数の値は
- すべての区間変数の値は
dumpコマンドを使用して表示できます。assignコマンドを使って区間変数に新しい値を代入することができます。- 区間式の値の表示はサポートしていません。
- 区間データ配列を表示する手段は提供していません。
- データ型に固有の機能でなければ、すべての一般的な機能が使用できます。
dbx機能に関する追加的な詳細については、「dbx コマンドによるデバッグ」を参照してください。大域的なプログラム検査
Sun WorkShop 6 の Fortran 95 における大域的なプログラム検査 (GPC) は、1 つの区間固有のエラーとして、ユーザー供給ルーチン呼び出しでの
コード例 1-15 INTERVAL 型の不一致INTERVAL型の不一致を検出します。
cat ce1-15.f95INTERVAL XX = [-1.0,+2.9]PRINT *,XCALL SUB(X)ENDSUBROUTINE SUB(Y)INTEGER Y(2)PRINT *,YENDmath%f95 -xia ce1-15.f95 -Xlist--- ce1-15.lst を参照 ---Global Call-Chain Considerata===============================1) <503> At line 4, MainPgm() calls SUB(fileline 6):MainPgm() sends argument 1 as type "Interval(16),"but SUB() expects type "Integer(4)"2) <507> At line 4, MainPgm() calls SUB(fileline 6):MainPgm() sends argument 1 as a "Scalar,"but SUB() expects a "1-D Array"Sun Fortran ライブラリで提供される区間機能
表 1-3 区間ライブラリ 区間組み込み配列関数 libifaiなし 区間組み込みライブラリ libsunimathなし
コードの移植とバイナリファイル
使用上対処の必要な、制限のある古い区間 Fortran コードが存在します。言語の構文と意味論が標準化されるまでは、異なる区間コンパイラ供給者のサポートが異なることは避けらません。お客様からの最も馴染みのある区間構文と意味論を考慮したフィードバックは標準化過程に役立ちます。区間演算の
READMEに一覧表示された電子メールのエイリアスに、コメントを送付することもできます。バイナリファイルでの区間の表現は、コンパイラがより狭い区間システムをサポートするかどうかにより異なります。
並列処理
このリリースでは、
-autoparコンパイラオプションは区間算術演算を含むループ処理に効果がありません。これらのループ処理は自動的には並列処理されません。明示的な並列化指令を付したループの並列化には、-explicitparコンパイラオプションを使用しなければなりません。エラーの検出
次のコード例では、区間固有のエラーメッセージを一覧表示しています。各コード例にはエラーメッセージとエラーを生成したコードが含まれています。
コード例 1-16 無効な終了点
コード例 1-17 区間と非区間の同値
cat ce1-16.f95INTERVAL :: I = [2., 1.]ENDmath%f95 -xia ce1-16.f95INTERVAL :: I = [2., 1.]^"ce1-14.f95", Line = 1, Column = 24: エラー:区間定数の左側の終了点は右 側の終了点以下でなければなりません。f90: コンパイル時間 0.150000 SECONDSf90: 最大フィールド長 4117346 10 進ワードf90: 2 ソース行f90: 1 個のエラー、0 個の警告、 0 個の他のメッセージ、 0 個のANSI
コード例 1-18 異なる KTPV を持つ区間オブジェクトの同値
cat ce1-17.f95INTERVAL :: IREAL :: REQUIVALENCE (I, R)ENDmath%f95 -xia ce1-17.f95EQUIVALENCE (I, R)^"ce1-15.f95", Line = 3, Column = 14: エラー: INTERVAL 実体 "I" と REAL 実体 "R" の結合指定は許可されません。f90: コンパイル時間 0.160000 SECONDSf90: 最大フィールド長 4117346 10 進ワードf90: 4 ソース行f90: 1 個のエラー、0 個の警告、 0 個の他のメッセージ、 0 個のANSI
コード例 1-19 厳密モードでの区間変数への REAL 式の代入
cat ce1-18.f95INTERVAL(4) :: I1INTERVAL(8) :: I2EQUIVALENCE (I1, I2)ENDmath%f95 -xia ce1-18.f95EQUIVALENCE (I1, I2)^"ce1-16.f95", Line = 3, Column = 14: エラー: 異なる種別型パラメータを 持つ INTERVAL 実体 "I1" と "I2" の結合指定はできません。f90: コンパイル時間 0.190000 SECONDSf90: 最大フィールド長 4117346 10 進ワードf90: 4 ソース行f90: 1 個のエラー、0 個の警告、 0 個の他のメッセージ、 0 個のANSI
コード例 1-20 厳密モードでの区間変数への区間式の代入
cat ce1-19.f95INTERVAL :: XREAL :: RX = RENDmath%f95 -xia=strict ce1-19.f95X = R^"ce1-17.f95", Line = 3, Column = 3: エラー: REAL 式を INTERVAL 変数 へ代入することは許可されません。f90: コンパイル時間 0.350000 SECONDSf90: 最大フィールド長 4117346 10 進ワードf90: 4 ソース行f90: 1 個のエラー、0 個の警告、 0 個の他のメッセージ、 0 個のANSI
cat ce1-20.f95INTERVAL :: XINTERVAL(16) :: yX = YENDmath%f95 -xia=strict ce1-20.f95X = Y^"ce1-18.f95", Line = 3, Column = 3: エラー: INTERVAL 変数に対する INTERVAL 式の代入はそれらが異なる種別型パラメータを持つ場合、許可されません。f90: コンパイル時間 0.170000 SECONDSf90: 最大フィールド長 4117346 10 進ワードf90: 4 ソース行f90: 1 個のエラー、0 個の警告、 0 個の他のメッセージ、 0 個のANSI既知の内部的なエラー
内部的なエラーが発生する可能性がある場合は常にコンパイル時の警告が出力される必要があります。このような警告が必要とされる状況は、最大幅要求式処理のスコープの外側で整数式を用いる場合です。
整数オーバーフロー
数の不正確性は、通常は
INTEGER式よりもむしろREAL式と関係します。しかしある意味では、INTEGER式はREAL式よりも危険です。REAL式がオーバーフローすると例外が提起されて IEEE 無限大が生成されます。例外はオーバーフローが発生したという警告です。無限大は、浮動小数点計算で潜在的な問題があることをユーザーに知らせます。オーバーフロー発生時にそれをトラップすることもできます。整数式がオーバーフローすると、それらは場合によっては、反対符号の値へと暗黙のうちに変換されてしまいます。さらに、逆の操作を実行して、すべての整数操作に関し同値テストを行うことが、整数式のオーバーフローの発生時期を検出する唯一の方法です。整数定数式の場合はコンパイル中に評価され、オーバーフローが検出されて警告メッセージが出力されるため安全です。
次の例は最大幅要求式処理のスコープが、
コード例 1-21 INTEGER オーバーフローの内部的なエラーINTEGER指数を使った ** 演算を含む、すべての組み込みのINTEGER演算と関数にまで拡張されると何が起きるのかを示しています。
cat ce1-21.f95INTERVAL :: X = [2], Y = [2]INTEGER :: I = HUGE(0)X = X**(I+1)Y = Y*(Y**I)IF(X .DJ. Y) PRINT *, "X and Y are disjoint."ENDmath%f95 -xia ce1-21.f95math%a.outX and Y are disjoint.このコード例はメッセージを表示しない内部的なエラーを示しています。最大幅要求式処理のスコープは、現在のところ ** 演算の整数指数にまで及ばないので、これは既知のエラーです。べき乗演算子に関する情報については、「べき乗演算子 X**N と X**Y」を参照してください。
注意 -このエラーは、Sun WorkShop 6 の Fortran 95 リリースではまだ修正されていません。また、警告メッセージも出力されません。
|
サン・マイクロシステムズ株式会社 Copyright information. All rights reserved. |
ホーム | 目次 | 前ページへ | 次ページへ | 索引 |