Using Sun Performance Library Fast Fourier Transform Routines

Using Sun Performance Library Fast Fourier Transform Routines

Many problems involve computing the discrete Fourier transform (DFT) of a periodic sequence of length N, where N is the number of data points or samples. The number of calculations required to compute the DFT is proportional to N². The fast Fourier transform (FFT) was developed to efficiently compute the DFT, where the number of calculations required to compute the FFT is proportional to Nlog₂N.

Sun Performance Library^TM provides routines for computing the FFT or inverse transform (synthesis) of a sequence of length N. The FFT routines are based on FFTPACK and VFFTPACK, which are collections of public domain subroutines available from Netlib (http://www.netlib.org). These routines have been enhanced and optimized for SPARC^TM platforms, and then bundled with the Sun Performance Library. The Sun Performance Library also includes two-dimensional FFT routines, three-dimensional FFT routines, and convolution and correlation routines.

This document describes how to use the Sun Performance Library FFT routines and provides examples of their use. This document does not describe the details of the FFT algorithms or the mathematics of the DFT. For more information on these topics, see the sources listed in References.

For information on the Fortran and C interfaces and types of arguments used with each FFT routine, see the section 3P man pages for the individual routines. For example, to display the man page for the RFFTI routine, type man -s 3P rffti. The man page routine names use lowercase letters.

Introduction to the FFTPACK and VFFTPACK Packages

Sun Performance Library contains FFT routines based on FFTPACK and VFFTPACK. Sun Performance Library also contains two-dimensional and three-dimensional FFT routines, which are not a part of FFTPACK or VFFTPACK.

FFTPACK routines operate on a single one-dimensional sequence of length N. After storing the sequence as a vector in an array, the fast sine, fast cosine, fast Fourier transform, or inverse transform of the sequence is computed. To process an additional sequence, the new sequence must be stored in the array before computing the FFT or inverse transform.

VFFTPACK routines are extensions of FFTPACK routines that operate on multiple one-dimensional sequences supplied simultaneously. Rather than storing and processing each sequence separately, the sequences are stored in a two-dimensional array, and then each sequence is processed.

VFFTPACK routines store the multiple one-dimensional sequences in a two-dimensional array, but the routines compute only a one-dimensional Fourier transform of each sequence. The two-dimensional and three-dimensional FFT routines provided with Sun Performance Library differ from the VFFTPACK routines. The two-dimensional FFT routines perform a two-dimensional Fourier transform of a sequence stored in a two-dimensional array, and the three-dimensional FFT routines perform a three-dimensional transform of a sequence stored in a three-dimensional array.

TABLE 1 summarizes some of the similarities and differences between the single vector FFTPACK, multiple vector VFFTPACK routines, two-dimensional FFT routines, and three-dimensional FFT routines.

TABLE 1   Comparison Between Single Vector and Multiple Vector Routines

Single Vector Multiple Vector

One-Dimensional Routines

Input Vector of length N An array of vectors

Output Single transform or inverse transform Multiple transforms or inverse transform (one transform or inverse transform per sequence)

Results Unnormalized^¹ Normalized

Two-Dimensional Routines

Input Two-dimensional array Multiple vector two-dimensional routines are not supported

Output Two-dimensional transform or inverse transform

Results Unnormalized

Three-Dimensional Routines

Input Three-dimensional array Multiple vector three-dimensional routines are not supported

Output Three-dimensional transform or inverse transform

Results Unnormalized

¹ Results of inverse transform must be divided by a normalization factor proportional to N.

Extensions to FFTPACK and VFFTPACK

Sun Performance Library provides the following extensions to the standard Netlib FFTPACK and VFFTPACK packages.

Double precision and double complex transforms. Because routines that process double precision and double complex data are not available in the standard package from Netlib, calls to these routines might not be portable.
Two-dimensional and three-dimensional FFTs. Netlib FFTPACK and VFFTPACK routines support one-dimensional FFTs.
Convolution and correlation routines.
Fortran 95 and C interfaces to FFTPACK and VFFTPACK. Conventions for these interfaces are described in detail in the Sun Performance Library User's Guide.
Optimizations for specific SPARC instruction set architectures.
Support for a 64-bit enabled Solaris^TM Operating Environment.
Support for parallel processing compiler options.
Support for multiple processor hardware options.

The Discrete Fourier Transform (DFT)

The FFT and VFFT routines provide an efficient means of computing the complex or real discrete Fourier transform and the discrete Fourier sine transform or discrete Fourier cosine transform of a real symmetric sequence.

The following definition of the DFT is used when calculating the complex discrete Fourier transform of a periodic sequence, where .

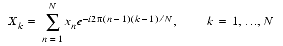
When calculating the inverse complex discrete Fourier transform, the following definition is used.

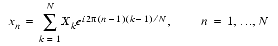
The results on the inverse transform are unnormalized and can be normalized by dividing each value by N.

When computing the DFT of a real sequence, the resulting array of Fourier coefficients is conjugate symmetric, where for k > 1, when using a one-based notation, or for k > 0, when using a zero-based notation. The asterisk * denotes complex conjugation, where . The number of calculations required to compute the DFT is reduced by taking advantage of this symmetry.

When computing the transform of a real sequence, the complex discrete Fourier transform can be rewritten in the real trigonometric form shown in TABLE 2. In TABLE 2, equals the real part of , equals the imaginary part of , and equals the real part of .

TABLE 2   Formulas for Real FFT Routines

Transform

Odd N ,

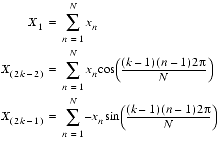
Even N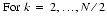

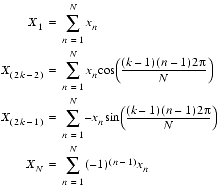
Inverse Transform

Odd N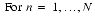

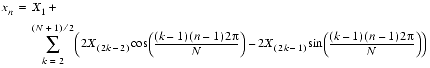
Even N ,

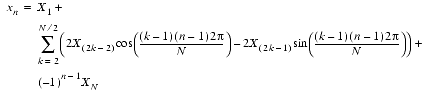
The FFT routines can be used to compute the discrete Fourier cosine transform, discrete Fourier sine transform, and inverse transforms of the functions listed in TABLE 3.

TABLE 3   Symmetries Supported by FFT and VFFT Routines
Symmetry Definition Trigonometric Expansion

Cosine Even-Wave An even function f(t) that satisfies the condition f(-t) = f(t). Trigonometric series containing only cosine terms.

Cosine Quarter-Wave A even function with half-wave symmetry , where T is the period of the function. Trigonometric series containing only cosine terms with odd wave numbers.

Sine Odd-Wave An odd function f(t) that satisfies the condition f(-t) =-f(t). Trigonometric series containing only sine terms.

Sine Quarter-Wave A odd function with half-wave symmetry . Trigonometric series containing only sine terms with odd wave numbers.

The formulas for the symmetries listed in TABLE 3 are shown in TABLE 4.

TABLE 4   Formulas for Symmetries Supported by FFT and VFFT Routines

Cosine Even-Wave^¹

Transform/
Inverse Transform
,

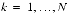
Cosine Quarter-Wave

Transform
,

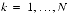
Inverse Transform
,

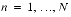
Sine Odd-Wave¹

Transform/
Inverse Transform
,

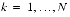
Sine Quarter-Wave

Transform
,

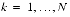
Inverse Transform
,

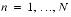
¹ Because the cosine even-wave and sine odd-wave routines perform either the transform or inverse transform, depending upon whether the input array contains the Fourier coefficients or the periodic sequence, only the notation for the transform is shown in this table.

For additional information on the formulas used to calculate the discrete transforms of symmetric sequences, see the documentation provided with FFTPACK, available on Netlib at http://www.netlib.org/fftpack/doc.

Naming Conventions

The name of each FFT or VFFT routine is made up of a base name that denotes the operation performed and a prefix that denotes the operand data type. For example, the routine CFFTF performs a fast Fourier transform of a complex sequence.

Prefixes used with FFT and VFFT base names are shown in TABLE 5.

TABLE 5   Prefix and Operand Data Types

Prefix Operand Data Type

FFT Routines No prefix REAL, REAL*4, REAL(4)

R REAL, REAL*4, REAL(4)

D DOUBLE, REAL*8, REAL(8)

C COMPLEX, COMPLEX*8, COMPLEX(4)

Z DOUBLE COMPLEX, COMPLEX*16, COMPLEX(8)

VFFT Routines VR REAL, REAL*4, REAL(4)

VD DOUBLE, REAL*8, REAL(8)

VC COMPLEX, COMPLEX*8, COMPLEX(4)

VZ DOUBLE COMPLEX, COMPLEX*16, COMPLEX(8)

FFT and VFFT base names are shown in TABLE 6. The last character of the base name is one of the following:

I: Initialize the Fourier transform or inverse Fourier transform routine
F: Compute the forward transform (the Fourier transform)
B: Compute the backward transform (the inverse Fourier transform or synthesis)

TABLE 6   FFT and VFFT Base Names
Base Name Operation

COSQB Inverse cosine quarter-wave transform (synthesis)

COSQF Cosine quarter-wave transform

COSQI Initialize cosine quarter-wave transform or inverse transform

COST Cosine even-wave transform

COSTI Initialize cosine even-wave transform

EZFFTB Inverse EZ transform (synthesis)

EZFFTF EZ transform

EZFFTI Initialize EZ transform

FFTB Inverse transform (synthesis)

FFTF Forward transform

FFTI Initialize before computing a transform or inverse transform

SINQB Inverse sine quarter-wave transform (synthesis)

SINQF Sine quarter-wave transform

SINQI Initialize sine quarter-wave transform or inverse transform

SINT Sine odd-wave transform

SINTI Initialize sine odd-wave transform

In this manual, the following conventions are used when referring to routines that exist for multiple data types:

The prefix x is added to the base name when the information applies to REAL, DOUBLE, COMPLEX, and DOUBLE COMPLEX versions of that routine.
Specific prefixes are listed in square brackets [ ] before the base name when information does not apply to all versions of the routine.

The following example shows samples of these naming conventions.

Convention Routines

xFFTF RFFTF, DFFTF, CFFTF, and ZFFTF

[R,D]FFTI RFFTI or DFFTI

[C,Z]FFTF CFFTF or ZFFTF

V[R,D,C,Z]FFTF VRFFTF, VDFFTF, VCFFTF, or VZFFTF

Sun Performance Library FFT Routines

Sun Performance Library contains the routines shown in TABLE 8. The data type of the arguments follows the conventions shown in TABLE 7.

TABLE 7   Argument Data Types
Argument Data Type

AZERO, A, B, R (EZFFT routines) Real

FULL, PLACE, ROWCOL Character

N, M, K, LDA, LD2A, LDB, LWORK, MDIMX Integer

A, B, X, XT Same as data type of routine called

WSAVE, WORK See TABLE 11

TABLE 8   FFT Routines
Routine Arguments Function

COSQB, DCOSQB N,X,WSAVE Inverse cosine quarter-wave transform

VCOSQB, VDCOSQB M,N,X,XT,MDIMX,WSAVE Inverse cosine quarter-wave transform (Vector)

COSQF, DCOSQF N,X,WSAVE Cosine quarter-wave transform

VCOSQF, VDCOSQF M,N,X,XT,MDIMX,WSAVE Cosine quarter-wave transform (Vector)

COSQI, DCOSQI N,WSAVE Initialize cosine quarter-wave transform and inverse transform

VCOSQI, VDCOSQI N,WSAVE Initialize cosine quarter-wave transform and inverse transform (Vector)

COST, DCOST N,X,WSAVE Cosine even-wave transform

VCOST, VDCOST M,N,X,XT,MDIMX,WSAVE Cosine even-wave transform (Vector)

COSTI, DCOSTI N,WSAVE Initialize cosine even-wave transform

VCOSTI, VDCOSTI N,WSAVE Initialize cosine even-wave transform (Vector)

EZFFTB N,R,AZERO,A,B,WSAVE EZ inverse Fourier transform

EZFFTF N,R,AZERO,A,B,WSAVE EZ Fourier transform

EZFFTI N,WSAVE Initialize EZ Fourier transform and inverse transform

RFFTB, DFFTB, CFFTB, ZFFTB N,X,WSAVE Inverse Fourier transform

VRFFTB, VDFFTB M,N,X,XT,MDIMX,WSAVE Inverse Fourier transform (Vector)

VCFFTB, VZFFTB M,N,X,XT,MDIMX, ROWCOL,WSAVE

RFFTF, DFFTF, CFFTF, ZFFTF N,X,WSAVE Fourier transform

VRFFTF, VDFFTF M,N,X,XT,MDIMX,WSAVE Fourier transform (Vector)

VCFFTF, VZFFTF M,N,X,XT,MDIMX, ROWCOL,WSAVE

RFFTI, DFFTI, CFFTI, ZFFTI N,WSAVE Initialize Fourier transform and inverse transform

VRFFTI, VDFFTI, VCFFTI, VZFFTI N,WSAVE Initialize Fourier transform and inverse transform (Vector)

SINQB, DSINQB N,X,WSAVE Inverse sine quarter-wave transform

VSINQB, VDSINQB M,N,X,XT,MDIMX,WSAVE Inverse sine quarter-wave transform (Vector)

SINQF, DSINQF N,X,WSAVE Sine quarter-wave transform

VSINQF, VDSINQF M,N,X,XT,MDIMX,WSAVE Sine quarter-wave transform (Vector)

SINQI, DSINQI N,WSAVE Initialize sine quarter-wave transform and inverse transform

VSINQI, VDSINQI N,WSAVE Initialize sine quarter-wave transform and inverse transform (Vector)

SINT, DSINT N,X,WSAVE Sine odd-wave transform

VSINT, VDSINT M,N,X,XT,MDIMX,WSAVE Sine odd-wave transform (Vector)

SINTI, DSINT N,WSAVE Initialize sine odd-wave transform

VSINTI, VDSINTI N,WSAVE Initialize sine odd-wave transform (Vector)

RFFT2B, DFFT2B PLACE,M,N,A,LDA, B,LDB,WORK,LWORK Inverse two-dimensional Fourier transform

CFFT2B, ZFFT2B M,N,A,LDA,WORK,LWORK

RFFT2F, DFFT2F PLACE,FULL,M,N,A,LDA, B,LDB,WORK,LWORK Two-dimensional Fourier transform

CFFT2F, ZFFT2F M,N,A,LDA,WORK,LWORK

RFFT2I, DFFT2I, CFFT2I, ZFFT2I M,N,WORK Initialize two-dimensional Fourier transform and inverse transform

RFFT3B, DFFT3B PLACE,M,N,K,A,LDA, B,LDB,WORK,LWORK Inverse three-dimensional Fourier transform

CFFT3B, ZFFT3B M,N,K,A,LDA,LD2A, WORK,LWORK

RFFT3F, DFFT3F PLACE,FULL,M,N,K, A,LDA,B,LDB,WORK,LWORK Three-dimensional Fourier transform

CFFT3F, ZFFT3F M,N,K,A,LDA,LD2A, WORK,LWORK

RFFT3I, DFFT3I, CFFT3I, ZFFT3I M,N,K,WORK Initialize three-dimensional Fourier transform and inverse transform

In addition to the FFT and VFFT routines listed in TABLE 8, the following routines are described in this manual.

TABLE 9   Convolution and Correlation Routines
Routine Arguments Function

SCNVCOR, DCNVCOR, CCNVCOR, ZCNVCOR CNVCOR,FOUR,NX,X,IFX, INCX,NY,NPRE,M,Y,IFY, INC1Y,INC2Y,NZ,K,Z, IFZ,INC1Z,INC2Z,WORK, LWORK Convolution or correlation of two vectors

SCNVCOR2, DCNVCOR2, CCNVCOR2, ZCNVCOR2 CNVCOR,METHOD,TRANSX, SCRATCHX,TRANSY, SCRATCHY,MX,NX,X,LDX, MY,NY,MPRE,NPRE,Y,LDY, MZ,NZ,Z,LDZ,WORKIN, LWORK Convolution or correlation of two matrices

Calling FFT Routines

FFT routines can be called using FORTRAN 77, Fortran 95, or C interfaces. 64-bit interfaces for compiling code that supports a 64-bit Solaris Operating Environment are also provided.

Fortran Interface Conventions

Sun Performance Library FORTRAN 77 and Fortran 95 interfaces use the following conventions:

All arguments are passed by reference.
The number of arguments to a routine is fixed.
Types of arguments must match.
Arrays are stored columnwise.
Indices are based at one, following standard Fortran practice.

C Interface Conventions

Sun Performance Library C interfaces use the following conventions:

Input-only scalars are passed by value rather than by reference. Complex and double complex arguments are not considered scalars because they are not implemented as a scalar type by C.
Complex scalars can be passed as either structures or arrays of length 2.
Types of arguments must match even after C does type conversion. For example, be careful when passing a single precision real value, because a C compiler can automatically promote the argument to double precision.
Arrays are stored columnwise. For Fortran programmers, this is the natural order in which arrays are stored. For C programmers, this is the transpose of the order in which they usually work. References in the documentation and man pages to rows refer to columns and vice versa.
Array indices are based at zero in conformance with C conventions, rather than being based at one in conformance with Fortran conventions.

Using 64-Bit FFT Routines

To compile code for a 64-bit enabled Solaris Operating Environment, use -xarch=v9[a|b] and convert all integer arguments to 64-bit arguments. 64-bit routines require the use of 64-bit integers.

Sun Performance Library provides 32-bit and 64-bit interfaces. To use the 64-bit interfaces:

Modify the Sun Performance Library routine name. For C, FORTRAN 77, and Fortran 95 code, append _64 to the names of Sun Performance Library routines (for example, rfftf_64 or CFFTB_64). For Fortran 95 code with the USE SUNPERF statement, routines can be called using the optional interfaces (interfaces where certain arguments can be omitted), but _64 must still be appended to the Sun Performance Library routine names. The compiler will infer the correct interface and values for the optional arguments, but the compiler cannot determine if the optional arguments are 32-bit integers or 64-bit integers.
Promote integers to 64 bits. Double precision variables and the real and imaginary parts of double complex variables are already 64 bits. Only the integers are promoted to 64 bits.

To control promotion of integer arguments, do one of the following:

To promote all default integers (integers declared without explicit byte sizes) from 32 bits to 64 bits, compile with -xtypemap=integer:64.
When using Fortran, to promote specific integers, change INTEGER or INTEGER*4 declarations to INTEGER*8.
Note – When calling a 32-bit interface, such as ZFFTF, from a 64-bit code, Sun Performance Library internally converts the arguments to 64 bits, and then calls the 64-bit interface (ZFFTF_64). Extra overhead is associated with this argument conversion.

Sequence Length N

The efficiency of the FFT routines depends upon the decomposition and length of the sequence N. Sun Performance Library FFT routines use the divide-and-conquer approach, where the transform of a sequence is a composite of transforms of shorter sequences.

The value of N affects the efficiency of the transform as follows:

If N can be factored into powers of 2, 3, 4, 5, 7, 11, or 13, the transform is computed using the FFT, which is an Nlog₂N operation.
If N is a product of some of these prime factors, along with additional prime factors, the part of N that can be factored into powers of 2, 3, 4, 5, 7, 11, or 13 is computed using the FFT. The transform of the sequence corresponding to the additional prime factors is computed using the DFT, which is an N² operation.
If N cannot be factored into powers of 2, 3, 4, 5, 7, 11, or 13, the transform of the sequence is computed using the DFT.

For example, the transform of a vector of length N = 1024 = 4 × 4 × 4 × 4 × 4 can be computed using an FFT, because 4 is a factor of 1024. If N = 6080 = 4 × 4 × 4 × 5 × 19, the transform of the vector corresponding to 4 × 4 × 4 × 5 is computed using the FFT, but the part of the vector corresponding to 19 is computed using the DFT. The transform of a vector of length N=1019 is computed using the DFT, because 1019 is not the product of small primes.

Computing the Fourier transform is most efficient when N-1 for fast cosine transforms, N+1 for fast sine transforms, and M, N, and K for multi-dimensional FFT routines can be factored into powers of 2, 3, 4, 5, 7, 11, or 13, as summarized in TABLE 10.

TABLE 10   Values That Must Have 2, 3, 4, 5, 7, 11, or 13 as Factors for Best Performance
Routine Values

COST, DCOST, VCOST, VDCOST N - 1

SINT, DSINT, VSINT, VDSINT N + 1

All other one-dimensional FFT and VFFT routines N

Two-dimensional FFT routines M and N

Three-dimensional FFT routines M, N, and K

The function xFFTOPT can be used to determine the optimal sequence length, as shown in CODE EXAMPLE 1.
CODE EXAMPLE 1 RFFTOPT Example

my_system% cat fft_ex01.f

PROGRAM TEST

C

INTEGER N, N1, N2, N3, RFFTOPT

C

N = 1024

N1 = 1019

N2 = 71

N3 = 49

C

PRINT *, 'N Original N Suggested'

PRINT '(I5, I12)', (N, RFFTOPT(N))

PRINT '(I5, I12)', (N1, RFFTOPT(N1))

PRINT '(I5, I12)', (N2, RFFTOPT(N2))

PRINT '(I5, I12)', (N3, RFFTOPT(N3))

C

END

my_system% f95 -dalign fft_ex01.f -xlic_lib=sunperf

my_system% a.out

N Original N Suggested

1024 1024

1019 1024

71 72

49 49
The size of the sequence affects performance. When N is small, such as 8 or 16, the overhead of calling the routine is large compared to the actual computational work performed by the routine. Also, when the size of N is too large for the data to fit in the cache, performance again degrades.

Work Array WSAVE for FFT and VFFT Routines

Each FFT or VFFT routine uses a work array that stores the tabulation of trigonometric functions computed while generating the Fourier transform or inverse transform. WSAVE also stores scratch (temporary) values generated during the transform or inverse transform.

Note – When using the VFFT routines, an extra work array, XT, is used to store temporary values generated from performing Fourier transforms or inverse transforms on multiple sequences.

Before performing the first transform or inverse transform:

1. Specify the minimum dimension and data type of the work array WSAVE.

The minimum dimension and data type depends upon the operand data type and FFT or VFFT routine, as shown in TABLE 11.

2. Initialize the work array by calling the corresponding FFT or VFFT routine whose base name ends with the character I.

For example, when using RFFTF or RFFTB, initialize the work array by calling RFFTI.
INTEGER N

REAL WSAVE (2 * N + 15)

CALL RFFTI (N, WSAVE)
When using CFFTF or CFFTB, initialize the work array by calling CFFTI.
INTEGER N

REAL WSAVE (4 * N + 15)

CALL CFFTI (N, WSAVE)
The same work array can be used for both the transform or inverse transform as long as N remains unchanged. Different WSAVE arrays are required for different values of N. As long as N and WSAVE remain unchanged, subsequent transforms can be obtained faster than the first transform, because the initialization does not have to be repeated between calls to the transform or inverse transform routines.

TABLE 11 Minimum Dimensions and Data Types for WSAVE Work Array
Routine Minimum Work Array Size (WSAVE) Type

One-Dimensional Routines

COSQI, DCOSQI 3N + 15 REAL, REAL*8

COSQB, DCOSQB 3N + 15 REAL, REAL*8

COSQF, DCOSQF 3N + 15 REAL, REAL*8

COST, DCOST 3N + 15 REAL, REAL*8

COSTI, DCOSTI 3N + 15 REAL, REAL*8

EZFFTB 3N + 15 REAL, REAL*8

EZFFTF 3N + 15 REAL, REAL*8

EZFFTI 3N + 15 REAL, REAL*8

RFFTB, DFFTB 2N + 15 REAL, REAL*8

RFFTF, DFFTF 2N + 15 REAL, REAL*8

RFFTI, DFFTI 2N + 15 REAL, REAL*8

CFFTB, ZFFTB 4N + 15 REAL, REAL*8

CFFTF, ZFFTF 4N + 15 REAL, REAL*8

CFFTI, ZFFTI 4N + 15 REAL, REAL*8

SINQB, DSINQB 3N + 15 REAL, REAL*8

SINQF, DSINQF 3N + 15 REAL, REAL*8

SINQI, DSINQI 3N + 15 REAL, REAL*8

SINT, DSINT 2N + N/2 + 15 REAL, REAL*8

SINTI, DSINTI 2N + N/2 + 15 REAL, REAL*8

VFFT Routines

VRFFTB, VDFFTB N + 15 REAL, REAL*8

VRFFTF, VDFFTF N + 15 REAL, REAL*8

VRFFTI, VDFFTI N + 15 REAL, REAL*8

VCFFTB, VZFFTB If transforming rows: 2 * M + 15If transforming columns: 2 * N + 15 REAL, REAL*8

VCFFTF, VZFFTF If transforming rows: 2 * M + 15If transforming columns: 2 * N + 15 REAL, REAL*8

VCFFTI, VZFFTI N + 15 REAL, REAL*8

VCOSQB, VDCOSQB 2 * N + 15 REAL, REAL*8

VCOSQF, VDCOSQF 2 * N + 15 REAL, REAL*8

VCOSQI, VDCOSQI 2 * N + 15 REAL, REAL*8

VCOST, VDCOST 2 * N + 15 REAL, REAL*8

VCOSTI, VDCOSTI 2 * N + 15 REAL, REAL*8

VSINQB, VDSINQB 2 * N + 15 REAL, REAL*8

VSINQF, VDSINQF 2 * N + 15 REAL, REAL*8

VSINQI, VDSINQI 2 * N + 15 REAL, REAL*8

VSINT, VDSINT N + N/2 + 15 REAL, REAL*8

VSINTI, VDSINTI N + N/2 + 15 REAL, REAL*8

Two-Dimensional Routines

RFFT2B, DFFT2B (M + 2N + MAX(M, 2N) + 30) REAL, REAL*8

RFFT2F, DFFT2F (M + 2N + MAX(M, 2N) + 30) REAL, REAL*8

RFFT2I, DFFT2I (M + 2N + MAX(M, 2N) + 30) REAL, REAL*8

CFFT2B, ZFFT2B (4 * (M + N) + 30) REAL, REAL*8

CFFT2F, ZFFT2F (4 * (M + N) + 30) REAL, REAL*8

CFFT2I, ZFFT2I (4 * (M + N) + 30) REAL, REAL*8

Three-Dimensional Routines

RFFT3B, DFFT3B (M + 2 * (N + K) + 4K + 45) REAL, REAL*8

RFFT3F, DFFT3F (M + 2 * (N + K) + 4K + 45) REAL, REAL*8

RFFT3I, DFFT3I (M + 2 * (N + K) + 30) REAL, REAL*8

CFFT3B, ZFFT3B (4 * (M + N + K) + 45) REAL, REAL*8

CFFT3F, ZFFT3F (4 * (M + N + K) + 45) REAL, REAL*8

CFFT3I, ZFFT3I (4 * (M + N + K) + 45) REAL, REAL*8

Parallelization

FFT and VFFT routines have been modified to take advantage of parallelization enhancements, as described in the Sun Performance Library User's Guide. FFT and VFFT routines can also be used in parallelized loops, as shown here.
CALL CFFTI (M, WSAVE)

C$PAR DOALL SHARED(M, WSAVE, N, C), PRIVATE(I)

DO I = 1, N

CALL CFFTF (M, C(1, I), WSAVE)

CALL CFFTB (M, C(1, I), WSAVE)

END DO
Note – The Fortran compiler parallelization features require a Sun WorkShop HPC license.

One-Dimensional FFT and Inverse Transform Routines

The routines in this section use the fast Fourier transform to compute the discrete Fourier transform and the inverse Fourier transforms. Routines are also available that compute the fast cosine transform, fast sine transform, and the inverses of these transforms.

Arguments for One-Dimensional FFT and VFFT Routines

FFT and VFFT routines use the arguments shown in TABLE 12. Some routines use additional arguments that are described in the sections for those routines.

TABLE 12 Arguments for FFT and VFFT Routines
Arguments Description

FFT Routines

N Length of the sequence to be transformed, where N 0.

X On entry, an array of length N containing the sequence to be transformed.

WSAVE On entry, a work array with a minimum dimension that depends upon the type of routine used and the data type of the operands. See TABLE 11 for a complete list of minimum work array dimensions.

VFFT Routines

N Length of the sequence to be transformed, where N 0.

M Number of sequences to be transformed, where M 0.

X A two-dimensional array X(M,N) whose rows contain the sequences to be transformed.

XT A two-dimensional work array with dimensions of (MDIMX * N).

MDIMX Leading dimension of the arrays X and XT as specified in a dimension or type statement, where MDIMX M.

WSAVE On entry, a work array with a minimum dimension that depends upon the type of routine used and the data type of the operands. See TABLE 11 for a complete list of minimum work array dimensions.

Data Storage for One-Dimensional FFT and VFFT Routines

The data storage format for the computed Fourier coefficients depends upon whether the sequence is complex or real.

Storage of Complex Sequences

The results of a complex one-dimensional FFT are stored in-place (in the original input array). Storage problems do not occur when performing the Fourier transform of a complex sequence, because the number of calculated Fourier coefficients equals the number of input values. The real and imaginary values of the Fourier coefficients can be stored in the original complex array without additional storage manipulations.

Storage of Real Sequences

Computing the Fourier transform of a real sequence produces complex Fourier coefficients. The number of computed Fourier coefficients is twice the number of values in the original sequence, because of the real and imaginary parts of the complex Fourier coefficients. The complex vector must be packed before it can be stored in the original real array. This packing is done by not storing the imaginary parts of the one or two Fourier coefficients that are always 0, and by not storing the complex conjugates of the Fourier coefficients.

Given a real sequence x_n, n = 0 : N - 1, of N data points, the transformed output X_k, k = 0 : N - 1, is packed and stored in the original array that holds the input data, as follows.

If N is even:

The real part of X₀is stored.
The imaginary part of X₀ is equal to 0; this part is not stored.
The real and imaginary parts of X₁, up to and including the real part of X₍_N_/2), are stored sequentially.
The imaginary part of X₍_N_/2) is equal to 0; this part is not stored.
X₍_N_-_k₎ is the complex conjugate of X_k, for k = 1 : N/2 - 1 and is not stored.

If N is odd,

The real part of X₀is stored.
The imaginary part of X₀ is equal to 0 and is not stored.
The real and imaginary parts of X₁, up to and including the imaginary part of X₍₍_N_-1)/2), are stored sequentially.
X₍_N_-_k₎ is the complex conjugate of X_k, for k = 1 : ((N-1)/2) - 1 and is not stored.

For example, if N = 6, the input array X contains the following six real data points:

X(1) = x₀

X(2) = x₁

X(3) = x₂

X(4) = x₃

X(5) = x₄

X(6) = x₅

Performing the Fourier transform computes the complex Fourier coefficients X₀, X₁, X₂, X₃, X₄, and X₅, each of which has a real (Re) part and an imaginary (Im) part. Following the transform, the complex Fourier coefficients are stored in the original real array X, as follows:

X(1) = Re(X₀)

X(2) = Re(X₁)

X(3) = Im(X₁)

X(4) = Re(X₂)

X(5) = Im(X₂)

X(6) = Re(X₃)

For even-length vectors, the resulting vector is conjugate-symmetric excluding the first element. The Fourier transform of the vector [1 2 3 4] is:

10+0i -2+2i -2+0i -2-2i

This is stored in a real vector as:

10 -2 2 -2

For odd-length vectors, the resulting vector is also conjugate-symmetric excluding the first element. For example, the Fourier transform of the vector [1 2 3 4 5] is:

15.0+0i -2.5+3.44i -2.5+.81i -2.5-.81i -2.5-3.44i

This is stored in a real vector as:

15 -2.5 3.44 -2.5 0.81

Note – When the transform of complex data is computed, the output is not packed. The transformed sequence contains the same number of real and complex values as the input sequence.

CODE EXAMPLE 2 computes the FFT and inverse of a real or complex sequence for even and odd values of N. The transform of the complex sequence shows all the Fourier coefficients in an unpacked, complex array. The transform of the real sequence shows the Fourier coefficients stored in a packed, real array. Differences between the real arrays for even and odd values of N can also be compared.
CODE EXAMPLE 2 Real and Complex FFT Example

my_system% cat fft_ex02.f

PROGRAM TEST

C

INTEGER I, N_EVEN, N_ODD

REAL XR(9), WORK(1000)

COMPLEX XC(9)

N_EVEN = 8

N_ODD = 9

XR(1:N_EVEN) = (/.60,.25,.74,.26,.14,.93,.28,.04/)

XC(1:N_EVEN) = (/.60,.25,.74,.26,.14,.93,.28,.04/)

C

CALL RFFTI(N_EVEN, WORK)

CALL RFFTF(N_EVEN, XR, WORK)

CALL CFFTI(N_EVEN, WORK)

CALL CFFTF(N_EVEN, XC, WORK)

PRINT 1000

PRINT '(F8.3)',XR(1:N_EVEN)

PRINT 1010

PRINT '(2F8.3,''I'')', (XC(1:N_EVEN))

XR(1:N_ODD) = (/.60,.25,.74,.26,.14,.93,.28,.04,.02/)

XC(1:N_ODD) = (/.60,.25,.74,.26,.14,.93,.28,.04,.02/)

C

CALL RFFTI(N_ODD, WORK)

CALL RFFTF(N_ODD, XR, WORK)

CALL CFFTI(N_ODD, WORK)

CALL CFFTF(N_ODD, XC, WORK)

PRINT 1020

PRINT '(F8.3)',XR(1:N_ODD)

PRINT 1030

PRINT '(2F8.3,''I'')', (XC(1:N_ODD))

1000 FORMAT (1X, "Transform of Real Sequence With Even N")

1010 FORMAT (1X, "Transform of Complex Sequence With Even N")

1020 FORMAT (1X, "Transform of Real Sequence With Odd N")

1030 FORMAT (1X, "Transform of Complex Sequence With Odd N")

C

END

my_system% f95 -dalign fft_ex02.f -xlic_lib=sunperf

my_system% a.out

Transform of real sequence with even N

3.240

-0.176

-0.135

-0.280

-0.880

1.096

0.785

0.280

Transform of complex sequence with even N

3.240 0.000i

-0.176 -0.135i

-0.280 -0.880i

1.096 0.785i

0.280 0.000i

1.096 -0.785i

-0.280 0.880i

-0.176 0.135i

Transform of real sequence with odd N

3.260

-0.333

-0.550

0.464

-0.991

0.080

1.091

0.860

-0.389

Transform of complex sequence with odd N

3.260 0.000i

-0.333 -0.550i

0.464 -0.991i

0.080 1.091i

0.860 -0.389i

0.860 0.389i

0.080 -1.091i

0.464 0.991i

-0.333 0.550i
CODE EXAMPLE 3 shows a C example that uses dfftf to compute the Fourier coefficients of a real sequence.
CODE EXAMPLE 3 C Example Showing How to Extract the Complex Result From the Packet Output of dfftf

my_system% cat fft_ex03.c

#include <sunperf.h>

#include <math.h>

#define N 16

/*

dfftf accepts as input a real vector of length N and

computes its discrete Fourier transform. Since the input

is real, the result of the transform will be conjugate symmetric.

The output of dfftf is a real vector of length N, which is a

packet representation of the complex FFT result. Only the first

half of the complex result is stored since the remaining values

can be obtained via the conjugate symmetry property. In

particular, if A[N] is the complex result of the FFT, the output

of dfftf is related to `a' as follows:

The real part of A[0] is stored in a[0].

A[1] is stored as two consecutive real numbers in a[1] and a[2].

A[2] is stored in a[3] and a[4].

If N is even, the real part of A[N/2-1] is stored in a[N-1]. If

N is odd, the real and imaginary parts of A[(N-1)/2] are stored

in a[N-2] and a[N-1] respectively.

The following example shows how to extract the complex result

from the packet output of dfftf for the case in which N even.

*/

void

main()

{

int i,j;

double a[N];

doublecomplex b[N];

double wa[2*N+15];

for (i=0;i<N;i++) {

a[i]=sin((double)i);

}

dffti(N,wa);

dfftf(N,a,wa);

/* extract the first N/2 complex values

from the packet representation */

b[0].r = a[0];

b[0].i = 0.0;

j=1;

for (i=1;i<N/2;i++) {

b[i].r = a[j];

b[i].i = a[j+1];

j += 2;

}

b[N/2].r = a[N-1];

b[N/2].i = 0.0;

/* extract the remaining N/2 values using the conjugate

symmetry */

for (i=N/2+1;i<N;i++) {

b[i].r = b[N-i].r;

b[i].i = -b[N-i].i;

}

}
FFT: Fast Fourier Transform Routines

The following routines use the fast Fourier transform to compute the discrete Fourier transform or inverse transform of a periodic sequence.

Routine Function

[R,D,C,Z]FFTI Initialize work array WSAVE for [R,D,C,Z]FFTF or [R,D,C,Z]FFTB

[R,D,C,Z]FFTF Compute Fourier coefficients of periodic sequence

[R,D,C,Z]FFTB Compute periodic sequence from Fourier coefficients

V[R,D,C,Z]FFTI Initialize work array for V[R,D,C,Z]FFTF or V[R,D,C,Z]FFTB

V[R,D,C,Z]FFTF Compute Fourier coefficients of multiple periodic sequences

V[R,D,C,Z]FFTB Compute multiple periodic sequences from Fourier coefficients

The xFFT and VxFFT routines, where x denotes R, D, C, or Z, use the arguments defined in Arguments for One-Dimensional FFT and VFFT Routines.

In addition to the VFFT arguments defined in Arguments for One-Dimensional FFT and VFFT Routines, the VCFFTF, VZFFTF, VCFFTB, and VZFFTB routines use one additional argument called ROWCOL. ROWCOL specifies whether to transform the rows or columns of X(M,N). Set ROWCOL equal to `R' or `r' perform the transform or inverse transform on the rows of X(M,N). Set ROWCOL equal to `C' or `c' perform the transform or inverse transform on the columns of X(M,N).

Normalization

The xFFT operations are unnormalized, so a call of xFFTF followed by a call of xFFTB will multiply the input sequence by N. The VxFFT operations are normalized, so a call of VxFFTF followed by a call of VxFFTB will return the original sequence.

Sample Programs: Fast Fourier Transform and Inverse Transform

CODE EXAMPLE 4 uses RFFTF to compute the FFT of a real sequence and RFFTB to compute the inverse transform. The computed Fourier coefficients are packed and stored in the original real array. The inverse transform is unnormalized and can be normalized by dividing each value by N.
CODE EXAMPLE 4 Fast Fourier Transform and Inverse Transform for Real Values

my_system% cat fft_ex04.f

PROGRAM TEST

C

INTEGER N

PARAMETER (N = 9)

C

INTEGER I

REAL PI, R(N), WSAVE(2 * N + 15)

C

EXTERNAL RFFTB, RFFTF, RFFTI

INTRINSIC ACOS, SIN

C

C Initialize array to a real sequence.

C

PI = ACOS (-1.0)

DO 100, I=1, N

R(I) = 3.0 + SIN ((I - 1.0) * 2.0 * PI / N)

100 CONTINUE

C

PRINT 1000

PRINT 1010, (R(I), I = 1, N)

CALL RFFTI (N, WSAVE)

CALL RFFTF (N, R, WSAVE)

PRINT 1020

PRINT 1010, (R(I), I = 1, N)

CALL RFFTB (N, R, WSAVE)

PRINT 1030

PRINT 1010, (R(I), I = 1, N)

C

1000 FORMAT (1X, 'Original Sequence R(I): ')

1010 FORMAT (1X, 100(F4.1, 1X))

1020 FORMAT (1X, 'Transformed Sequence: ')

1030 FORMAT (1X, 'Unnormalized Recovered Sequence (R(I)*N): ')

C

END

my_system% f95 -dalign fft_ex04.f -xlic_lib=sunperf

my_system% a.out

Original Sequence R(I):

3.0 3.6 4.0 3.9 3.3 2.7 2.1 2.0 2.4

Transformed Sequence:

27.0 0.0 -4.5 0.0 0.0 0.0 0.0 0.0 0.0

Unnormalized Recovered Sequence (R(I)*N):

27.0 32.8 35.9 34.8 30.1 23.9 19.2 18.1 21.2
CODE EXAMPLE 5 uses CFFTF to compute the FFT of a complex sequence and CFFTB to compute the inverse transform. Because the number of calculated Fourier coefficients equals the number of input values, the real and imaginary values of the Fourier coefficients can be stored in the original array without additional storage manipulations. The inverse transform is unnormalized and can be normalized by dividing each value by N.
CODE EXAMPLE 5 Fast Fourier Transform and Inverse Transform for Complex Values

my_system% cat fft_ex05.f

PROGRAM TEST

C

INTEGER N

PARAMETER (N = 4)

C

INTEGER I

REAL PI, WSAVE(4 * N + 15), X, Y

COMPLEX C(N)

C

EXTERNAL CFFTB, CFFTF, CFFTI

INTRINSIC ACOS, CMPLX, COS, SIN

C

C Initialize the array C to a complex sequence.

C

PI = ACOS (-1.0)

DO 100, I=1, N

X = SIN ((I - 1.0) * 2.0 * PI / N)

Y = COS ((I - 1.0) * 2.0 * PI / N)

C(I) = CMPLX (X, Y)

100 CONTINUE

C

PRINT 1000

PRINT 1010, (C(I), I = 1, N)

CALL CFFTI (N, WSAVE)

CALL CFFTF (N, C, WSAVE)

PRINT 1020

PRINT 1010, (C(I), I = 1, N)

CALL CFFTB (N, C, WSAVE)

PRINT 1030

PRINT 1010, (C(I), I = 1, N)

C

1000 FORMAT (1X, 'Original Sequence C(I):')

1010 FORMAT (1X, 100(F5.1, ' +',F4.1,'i '))

1020 FORMAT (1X, 'Transformed Sequence:')

1030 FORMAT (1X, 'Unnormalized Recovered Sequence (C(I)*N):')

C

END

my_system% f95 -dalign fft_ex05.f -xlic_lib=sunperf

my_system% a.out

Original Sequence C(I):

0.0 + 1.0i 1.0 + 0.0i 0.0 +-1.0i -1.0 + 0.0i

Transformed Sequence:

0.0 + 0.0i 0.0 + 0.0i 0.0 + 0.0i 0.0 + 4.0i

Unnormalized Recovered Sequence (C(I)*N):

0.0 + 4.0i 4.0 + 0.0i 0.0 +-4.0i -4.0 + 0.0i
EZFFT: EZ Fourier Transform Routines

The following routines are used to perform a Fourier transform or inverse transform of a real periodic sequence. The EZ Fourier or inverse transform routines are simplified but slower versions of the Fast Fourier Transform routines.

Routine Function

EZFFTI Initialize work array WSAVE for EZFFTF or EZFFTB

EZFFTF Compute Fourier coefficients of periodic sequence

EZFFTB Compute periodic sequence from Fourier coefficients

The EZFFT routines use the arguments shown in TABLE 13.

TABLE 13 Arguments for EZFFT Routines
Argument Definition

N Sequence length

R For EZFFTF, a real array containing the sequence to be transformed, unchanged on exit. For EZFFTB, a real array containing the Fourier coefficients of the inputs.

AZERO The Fourier constant A₀

A Real array containing the real parts of the complex Fourier coefficients. If N is even, then A is length N/2, otherwise A is length (N-1)/2.

B Real array containing the imaginary parts of the complex Fourier coefficients. If N is even, then B is length N/2, otherwise B is length (N-1)/2.

WSAVE Work array initialized by EZFFTI

Sample Program: EZ Fourier Transform and Inverse Transform

CODE EXAMPLE 6 uses EZFFTF to compute a Fourier transform of a real sequence and EZFFTB to compute the inverse transform. When using EZFFTF, the computed Fourier coefficients are stored in the arrays A and B. The input array R is not overwritten. Unlike the output of RFFTF and DFFTF, no packing is performed, and the complex conjugates are retained.
CODE EXAMPLE 6 EZ Fourier Transform and Inverse Transform

my_system% cat fft_ex06.f

PROGRAM TEST

C

INTEGER N

PARAMETER (N = 9)

C

INTEGER I

REAL A(N), B(N), AZERO, PI, R(N)

REAL WSAVE(3 * N + 15)

C

EXTERNAL EZFFTB, EZFFTF, EZFFTI

INTRINSIC ACOS, COS, SIN

C

C Initialize array to a sequence of real numbers.

C

PI = ACOS (-1.0)

DO 100, I=1, N

R(I) = 3.0 + SIN ((I - 1.0) * 2.0 * PI / N) +

$ 4.0 * COS ((I - 1.0) * 8.0 * PI / N)

100 CONTINUE

C

CALL EZFFTI (N, WSAVE)

PRINT 1000

PRINT 1010, (R(I), I = 1, N)

CALL EZFFTF (N, R, AZERO, A, B, WSAVE)

PRINT 1020, AZERO

PRINT 1030

PRINT 1010, (A(I), I = 1, N)

PRINT 1040

PRINT 1010, (B(I), I = 1, N)

CALL EZFFTB (N, R, AZERO, A, B, WSAVE)

PRINT 1050

PRINT 1010, (R(I), I = 1, N)

C

1000 FORMAT (1X, 'Original Sequence: ')

1010 FORMAT (100(F6.1, 1X))

1020 FORMAT (1X, 'Azero = ', F4.1)

1030 FORMAT (1X, 'A = ')

1040 FORMAT (1X, 'B = ')

1050 FORMAT (1X, 'Recovered Sequence: ')

C

END

my_system% f95 -dalign fft_ex06.f -xlic_lib=sunperf

my_system% a.out

Original Sequence:

7.0 -0.1 7.0 1.9 4.0 3.4 0.1 5.1 -1.4

Azero = 3.0

A =

0.0 0.0 0.0 4.0 0.0 0.0 0.0 0.0 0.0

B =

1.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0

Recovered Sequence:

7.0 -0.1 7.0 1.9 4.0 3.4 0.1 5.1 -1.4
COSQ: Cosine Quarter-Wave Routines

The following routines are used to perform a discrete Fourier cosine transform or inverse transform of a cosine series with only odd wave numbers.

Routine Function

[D]COSQI Initialize work array WSAVE for [D]COSQF or [D]COSQB

[D]COSQF Compute Fourier coefficients of cosine series with odd wave numbers

[D]COSQB Compute periodic sequence from Fourier coefficients

V[D]COSQI Initialize work array for V[D]COSQF or V[D]COSQB

V[D]COSQF Compute Fourier coefficients of multiple cosine series with odd wave numbers

V[D]COSQB Compute multiple periodic sequences from Fourier coefficients

Because of the assumption of symmetry, the sequence used as input to the cosine quarter-wave routine only needs to contain the part of the sequence that is sufficient to determine the entire sequence.

Normalization

The xCOSQ operations are unnormalized inverses of themselves, so a call to xCOSQF followed by a call to xCOSQB will multiply the input sequence by 4 × N. The VxCOSQ operations are normalized, so a call of VxCOSQF followed by a call of VxCOSQB will return the original sequence.

Sample Programs: Cosine Quarter-Wave Transform and Inverse Transform

CODE EXAMPLE 7 uses COSQF to compute the cosine quarter-wave transform of a real sequence and COSQB to compute the inverse transform. The computed Fourier coefficients are packed and stored in the original real array. The inverse transform is unnormalized and can be normalized by dividing each value by 4*N.
CODE EXAMPLE 7 Cosine Quarter-Wave Transform and Inverse Transform

my_system% cat fft_ex07.f

PROGRAM TEST

C

INTEGER N

PARAMETER (N = 6)

INTEGER I

REAL PI, WSAVE(3 * N + 15), X(N)

C

EXTERNAL COSQB, COSQF, COSQI

INTRINSIC ACOS, COS

C

C Initialize array X to a real even quarter-wave sequence,

C that is, it can be expanded in terms of a cosine series

C with only odd wave numbers.

C

PI = ACOS (-1.0)

DO 100, I=1, N

X(I) = COS((I - 1) * PI / (2.0 * N))

100 CONTINUE

C

CALL COSQI (N, WSAVE)

PRINT 1000

PRINT 1010, (X(I), I = 1, N)

CALL COSQF (N, X, WSAVE)

PRINT 1020

PRINT 1010, (X(I), I = 1, N)

CALL COSQB (N, X, WSAVE)

PRINT 1030

PRINT 1010, (X(I), I = 1, N)

C

1000 FORMAT(1X, 'Original Sequence: ')

1010 FORMAT(1X, 100(F7.3, 1X))

1020 FORMAT(1X, 'Transformed Sequence: ')

1030 FORMAT(1X, 'Recovered Sequence: ')

END

my_system% f95 -dalign fft_ex07.f -xlic_lib=sunperf

my_system% a.out

Original Sequence:

1.000 0.966 0.866 0.707 0.500 0.259

Transformed Sequence:

6.000 0.000 0.000 0.000 0.000 0.000

Recovered Sequence:

24.000 23.182 20.785 16.971 12.000 6.212
CODE EXAMPLE 8 uses VCOSQF to compute the cosine quarter-wave transform of a single real sequence and VCOSQB to compute the inverse transform. The computed Fourier coefficients are packed and stored in the original real array. The inverse transform is normalized.
CODE EXAMPLE 8 Cosine Quarter-Wave Transform and Inverse Transform Using Vector Routines

my_system% cat fft_ex08.f

PROGRAM TEST

C

INTEGER M, N

PARAMETER (M = 1)

PARAMETER (N = 6)

C

INTEGER I

REAL PI, WSAVE(3 * N + 15), X(M, N), XT(M, N)

C

EXTERNAL VCOSQB, VCOSQF, VCOSQI

INTRINSIC ACOS, COS

C

C Initialize the first row of the array to a real even

C quarter-wave sequence, that is, it can be expanded in

C terms of a cosine series with only odd wave numbers.

C

PI = ACOS (-1.0)

DO 100, I=1, N

X(M,I) = 40.0 * COS ((I - 1) * PI / (2.0 * N))

100 CONTINUE

C

PRINT 1000

PRINT 1010, (X(M, I), I = 1, N)

CALL VCOSQI (N, WSAVE)

CALL VCOSQF (M, N, X, XT, M, WSAVE)

PRINT 1020

PRINT 1010, (X(M, I), I = 1, N)

CALL VCOSQB (M, N, X, XT, M, WSAVE)

PRINT 1030

PRINT 1010, (X(M, I), I = 1, N)

C

1000 FORMAT (1X, 'Original Sequence: ')

1010 FORMAT (1X, 100(F5.1, 1X))

1020 FORMAT (1X, 'Transformed Sequence: ')

1030 FORMAT (1X, 'Recovered Sequence: ')

C

END

my_system% f95 -dalign fft_ex08.f -xlic_lib=sunperf

my_system% a.out

Original Sequence:

40.0 38.6 34.6 28.3 20.0 10.4

Transformed Sequence:

49.0 0.0 0.0 0.0 0.0 0.0

Recovered Sequence:

40.0 38.6 34.6 28.3 20.0 10.4
CODE EXAMPLE 9 uses VCOSQF to compute the cosine quarter-wave transform of multiple real sequences and VCOSQB to compute the inverse transforms. The computed Fourier coefficients of each sequence are packed and stored in the rows of the original real array. The inverse transforms are normalized.
CODE EXAMPLE 9 Cosine Quarter-Wave Transform and Inverse Transform Using Vector Routines

my_system% cat fft_ex09.f

PROGRAM TEST

C

INTEGER M, N

PARAMETER (M = 4)

PARAMETER (N = 6)

C

INTEGER I, J

REAL PI, WSAVE(N + 15), X(M, N), XT(M, N)

C

EXTERNAL VCOSQB, VCOSQF, VCOSQI

INTRINSIC ACOS, COS

C

C Initialize the array to m real even quarter-wave sequences,

C that is, they can be expanded in terms of a cosine series

C with only odd wave numbers.

C

PI = ACOS (-1.0)

DO 110, J=1, M

DO 100, I=1, N

X(J,I) = 40.0 * J * COS ((I-1) * PI / 2.0 / N )

100 CONTINUE

110 CONTINUE

C

CALL VCOSQI (N, WSAVE)

PRINT 1000

DO 120, J=1, M

PRINT 1010, J, (X(J, I), I = 1, N)

120 CONTINUE

CALL VCOSQF (M, N, X, XT, M, WSAVE)

PRINT 1020

DO 130, J=1, M

PRINT 1010, J, (X(J, I), I = 1, N)

130 CONTINUE

CALL VCOSQB (M, N, X, XT, M, WSAVE)

PRINT 1030

DO 140, J=1, M

PRINT 1010, J, (X(J, I), I = 1, N)

140 CONTINUE

C

1000 FORMAT (1X, 'Original Sequence: ')

1010 FORMAT(1X, ' Sequence', I2, ': ', 100(F5.1, 1X))

1020 FORMAT (1X, 'Transformed Sequence: ')

1030 FORMAT (1X, 'Recovered Sequence: ')

C

END

my_system% f95 -dalign fft_ex09.f -xlic_lib=sunperf

my_system% a.out

Original Sequence:

Sequence 1: 40.0 38.6 34.6 28.3 20.0 10.4

Sequence 2: 80.0 77.3 69.3 56.6 40.0 20.7

Sequence 3: 120.0 115.9 103.9 84.9 60.0 31.1

Sequence 4: 160.0 154.5 138.6 113.1 80.0 41.4

Transformed Sequence:

Sequence 1: 49.0 0.0 0.0 0.0 0.0 0.0

Sequence 2: 98.0 0.0 0.0 0.0 0.0 0.0

Sequence 3: 147.0 0.0 0.0 0.0 0.0 0.0

Sequence 4: 196.0 0.0 0.0 0.0 0.0 0.0

Recovered Sequence:

Sequence 1: 40.0 38.6 34.6 28.3 20.0 10.4

Sequence 2: 80.0 77.3 69.3 56.6 40.0 20.7

Sequence 3: 120.0 115.9 103.9 84.9 60.0 31.1

Sequence 4: 160.0 154.5 138.6 113.1 80.0 41.4
COST: Cosine Even-Wave Routines

The following routines are used to perform a discrete fourier cosine transform of an even sequence.

Routine Function

[D]COSTI Initialize work array WSAVE for [D]COSTF or [D]COSTB

[D]COST Compute the Fourier coefficients or inverse transform of an even sequence

V[D]COSTI Initialize work array for V[D]COSTF or V[D]COSTB

V[D]COST Compute Fourier coefficients or inverse transform of multiple even sequences

The cosine even-wave routines are their own inverse. xCOST computes the Fourier coefficients from a periodic sequence or the periodic sequence from the Fourier coefficients. xCOSTF and xCOSTB routines do not exist for cosine even-wave transforms.

Because of the assumption of symmetry, the sequence used as input to the cosine even-wave routine only needs to contain the part of the sequence that is sufficient to determine the entire sequence.

Normalization

The xCOST transforms are unnormalized inverses of themselves, so a call of xCOST followed by another call of xCOST will multiply the input sequence by 2 × (N-1). The VxCOST transforms are normalized, so a call of VxCOST followed by a call of VxCOST will return the original sequence.

Sample Program: Cosine Even-Wave Transform and Inverse Transform

CODE EXAMPLE 10 uses COST to compute the cosine even-wave transform of a real sequence and the inverse transform. The computed Fourier coefficients are packed and stored in the original real array. The inverse transform is unnormalized and can be normalized by dividing each value by 2*(N-1).
CODE EXAMPLE 10 Cosine Even-Wave Transform and Inverse Transform

my_system% cat fft_ex10.f

PROGRAM TEST

C

INTEGER N

PARAMETER (N = 9)

INTEGER I

REAL PI, X(N), WSAVE(3 * N + 15)

C

EXTERNAL COST, COSTI

INTRINSIC ACOS, COS

C

C Initialize the array X to an even sequence, that is, it

C can be expanded in terms of a trigonometric series that

C contains only cosine terms.

C

PI = ACOS (-1.0)

DO 100, I=1, N

X(I) = COS ((I - 1.0) * 2.0 * PI / (N - 1.0))

100 CONTINUE

C

CALL COSTI (N, WSAVE)

PRINT 1000

PRINT 1010, (X(I), I = 1, N)

CALL COST (N, X, WSAVE)

PRINT 1020

PRINT 1010, (X(I), I = 1, N)

CALL COST (N, X, WSAVE)

PRINT 1030

PRINT 1010, (X(I), I = 1, N)

C

1000 FORMAT (1X, 'Original Sequence: ')

1010 FORMAT (1X, 100(F5.1, 1X))

1020 FORMAT (1X, 'Transformed Sequence: ')

1030 FORMAT (1X, 'Recovered Sequence: ')

END

my_system% f95 -dalign fft_ex10.f -xlic_lib=sunperf

my_system% a.out

Original Sequence:

1.0 0.7 0.0 -0.7 -1.0 -0.7 0.0 0.7 1.0

Transformed Sequence:

0.0 0.0 8.0 0.0 0.0 0.0 0.0 0.0 0.0

Recovered Sequence:

16.0 11.3 0.0 -11.3 -16.0 -11.3 0.0 11.3 16.0
SINQ: Sine Quarter-Wave Routines

The following routines are used to compute a a discrete Fourier sine transform or inverse transform of a of a sine series that contains only odd wave numbers.

Routine Function

[D]SINQI Initialize work array WSAVE for [D]SINQF or [D]SINQB

[D]SINQF Compute Fourier coefficients of sine series with only odd wave numbers

[D]SINQB Compute periodic sequence from Fourier coefficients

V[D]SINQI Initialize work array for V[D]SINQF or V[D]SINQB

V[D]SINQF Compute Fourier coefficients of multiple sine series with only odd wave numbers

V[D]SINQB Compute multiple periodic sequences from Fourier coefficients

Because of the assumption of symmetry, the sequence used as input to the sine quarter-wave routine only needs to contain the part of the sequence that is sufficient to determine the entire sequence.

Normalization

The xSINQ operations are unnormalized inverses of themselves, so a call to xSINQF followed by a call to xSINQB will multiply the input sequence by 4 × N. The VxSINQ operations are normalized, so a call of VxSINQF followed by a call of VxSINQB will return the original sequence.

Sample Programs: Sine Quarter-Wave Transform and Inverse Transform

CODE EXAMPLE 11 uses SINQF to compute sine quarter-wave transform of a real sequence and SINQB to compute the inverse transform. The computed Fourier coefficients are packed and stored in the original real array. The inverse transform is unnormalized and can be normalized by dividing each value by 4*N.
CODE EXAMPLE 11 Sine Quarter-Wave Transform and Inverse Transform

my_system% cat fft_ex11.f

PROGRAM TEST

C

INTEGER N

PARAMETER (N = 6)

INTEGER I

REAL PI, WSAVE(3 * N + 15), X(N)

C

EXTERNAL SINQB, SINQF, SINQI

INTRINSIC ACOS, SIN

C

C Initialize array X to a real odd quarter-wave sequence,

C that is, it can be expanded in terms of a sine series with

C only odd wave number.

C

PI = ACOS (-1.0)

DO 100, I=1, N

X(I) = 40.0 * SIN (I * PI / (2.0 * N))

100 CONTINUE

C

PRINT 1000

PRINT 1010, (X(I), I = 1, N)

CALL SINQI (N, WSAVE)

CALL SINQF (N, X, WSAVE)

PRINT 1020

PRINT 1010, (X(I), I = 1, N)

CALL SINQB(N, X, WSAVE)

PRINT 1030

PRINT 1010, (X(I), I = 1, N)

C

1000 FORMAT (1X, 'Original Sequence: ')

1010 FORMAT (1X, 100(F6.1, 1X))

1020 FORMAT (1X, 'Transformed Sequence: ')

1030 FORMAT (1X, 'Recovered Sequence: ')

C

END

my_system% f95 -dalign fft_ex11.f -xlic_lib=sunperf

my_system% a.out

Original Sequence:

10.4 20.0 28.3 34.6 38.6 40.0

Transformed Sequence:

240.0 0.0 0.0 0.0 0.0 0.0

Recovered Sequence:

248.5 480.0 678.8 831.4 927.3 960.0
CODE EXAMPLE 12 uses VSINQF to compute the sine quarter-wave transform of a single real sequence and VSINQB to compute the inverse transform. The computed Fourier coefficients are packed and stored in the original real array. The inverse transform is normalized.
CODE EXAMPLE 12 Sine Quarter-Wave Transform and Inverse Transform Using Vector Routines

my_system% cat fft_ex12.f

PROGRAM TEST

C

INTEGER M, N

PARAMETER (M = 1)

PARAMETER (N = 6)

C

INTEGER I

REAL PI, WSAVE(N + 15), X(M, N), XT(M, N)

C

EXTERNAL VSINQB, VSINQF, VSINQI

INTRINSIC ACOS, SIN

C

C Initialize the first row of the array to a real odd

C quarter-wave sequence, that is, it can be expanded in

C terms of a cosine series with only odd wave numbers.

C

PI = ACOS (-1.0)

DO 100, I=1, N

X(M,I) = 40.0 * SIN ((I * PI / (2.0 * N)))

100 CONTINUE

C

CALL VSINQI (N, WSAVE)

PRINT 1000

PRINT 1010, (X(M, I), I = 1, N)

CALL VSINQF (M, N, X, XT, M, WSAVE)

PRINT 1020

PRINT 1010, (X(M, I), I = 1, N)

CALL VSINQB (M, N, X, XT, M, WSAVE)

PRINT 1030

PRINT 1010, (X(M, I), I = 1, N)

C

1000 FORMAT (1X, 'Original Sequence: ')

1010 FORMAT (1X, 100(F5.1, 1X))

1020 FORMAT (1X, 'Transformed Sequence: ')

1030 FORMAT (1X, 'Recovered Sequence: ')

C

END

my_system% f95 -dalign fft_ex12.f -xlic_lib=sunperf

my_system% a.out

Original Sequence:

10.4 20.0 28.3 34.6 38.6 40.0

Transformed Sequence:

49.0 0.0 0.0 0.0 0.0 0.0

Recovered Sequence:

10.4 20.0 28.3 34.6 38.6 40.0
CODE EXAMPLE 13 uses VSINQF to compute the sine quarter-wave transform of multiple real sequences and VSINQB to compute the inverse transforms. The computed Fourier coefficients of each sequence are packed and stored in the rows of the original real array. The inverse transforms are normalized.
CODE EXAMPLE 13 Sine Quarter-Wave Transform and Inverse Transform Using Vector Routines

my_system% cat fft_ex13.f

PROGRAM TEST

INTEGER M, N

PARAMETER (M = 4)

PARAMETER (N = 6)

INTEGER I, J

REAL PI, WSAVE(N + 15), X(M, N+1), XT(M, N + 1)

C

EXTERNAL VSINQB, VSINQF, VSINQI

INTRINSIC ACOS, SIN

C

C Initialize the array to m real odd quarter-wave sequence,

C that is, they can be expanded in terms of a cosine series

C with only odd wave numbers.

C

PI = ACOS (-1.0)

DO 110, J=1, M

DO 100, I=1, N

X(J,I) = 40.0 * J * SIN (I * PI / (2.0 * N))

100 CONTINUE

110 CONTINUE

C

CALL VSINQI (N, WSAVE)

PRINT 1000

DO 120, J=1, M

PRINT 1010, J, (X(J, I), I = 1, N)

120 CONTINUE

CALL VSINQF (M, N, X, XT, M, WSAVE)

PRINT 1020

DO 130, J=1, M

PRINT 1010, J, (X(J, I), I = 1, N)

130 CONTINUE

CALL VSINQB (M, N, X, XT, M, WSAVE)

PRINT 1030

DO 140, J=1, M

PRINT 1010, J, (X(J, I), I = 1, N)

140 CONTINUE

C

1000 FORMAT (1X, 'Original Sequence: ')

1010 FORMAT (1X, ' Sequence', I2, ': ', 100(F5.1, 1X))

1020 FORMAT (1X, 'Transformed Sequence: ')

1030 FORMAT (1X, 'Recovered Sequence: ')

C

END

my_system% f95 -dalign fft_ex13.f -xlic_lib=sunperf

my_system% a.out

Original Sequence:

Sequence 1: 10.4 20.0 28.3 34.6 38.6 40.0

Sequence 2: 20.7 40.0 56.6 69.3 77.3 80.0

Sequence 3: 31.1 60.0 84.9 103.9 115.9 120.0

Sequence 4: 41.4 80.0 113.1 138.6 154.5 160.0

Transformed Sequence:

Sequence 1: 49.0 0.0 0.0 0.0 0.0 0.0

Sequence 2: 98.0 0.0 0.0 0.0 0.0 0.0

Sequence 3: 147.0 0.0 0.0 0.0 0.0 0.0

Sequence 4: 196.0 0.0 0.0 0.0 0.0 0.0

Recovered Sequence:

Sequence 1: 10.4 20.0 28.3 34.6 38.6 40.0

Sequence 2: 20.7 40.0 56.6 69.3 77.3 80.0

Sequence 3: 31.1 60.0 84.9 103.9 115.9 120.0

Sequence 4: 41.4 80.0 113.1 138.6 154.5 160.0
SINT: Sine Odd-Wave Transform Routines

The following routines are used to perform a discrete Fourier sine transform of an odd sequence.

Routine Function

[D]SINTI Initialize work array WSAVE for [D]SINQF or [D]SINQB

[D]SINT Compute the Fourier coefficients or inverse transform of a sine series with only odd wave numbers

V[D]SINTI Initialize work array for V[D]SINQF or V[D]SINQB

V[D]SINT Compute the Fourier coefficients or inverse transform of multiple sine series with only odd wave numbers

The sine odd-wave routines are their own inverse. xSINT computes the Fourier coefficients from a periodic sequence or the periodic sequence from the Fourier coefficients. xSINTF and xSINTB routines do not exist for sine odd-wave transforms.

Because of the assumption of symmetry, the sequence used as input to the sine odd-wave routine only needs to contain the part of the sequence that is sufficient to determine the whole sequence.

Normalization

The xSINT transforms are unnormalized inverses of themselves, so a call of xSINT followed by another call of xSINT will multiply the input sequence by 2 × (N+1). The VxSINT transforms are normalized, so a call of VxSINT followed by a call of VxSINT will return the original sequence.

Sample Program: Sine Odd-Wave Transform

CODE EXAMPLE 14 uses SINT to compute the sine odd-wave transform of a real sequence and the inverse transform. The computed Fourier coefficients are packed and stored in the original real array. The inverse transform is unnormalized and can be normalized by dividing each value by 2*(N+1).
CODE EXAMPLE 14 Sine Odd-Wave Transform and Inverse Transform

my_system% cat fft_ex14.f

PROGRAM TEST

C

INTEGER N

PARAMETER (N = 9)

C

INTEGER I

REAL PI, WSAVE(3 * N + 15), X(N)

C

EXTERNAL SINT, SINTI

INTRINSIC ACOS, SIN

C

C Initialize the array X to an odd sequence, that is, it

C can be expanded in terms of a trigonometric series that

C contains only sine terms.

C

PI = ACOS (-1.0)

DO 100, I=1, N

X(I) = SIN ( I * 2.0 * PI / (N + 1.0))

100 CONTINUE

C

PRINT 1000

PRINT 1010, (X(I), I = 1, N)

CALL SINTI (N, WSAVE)

CALL SINT (N, X, WSAVE)

PRINT 1020

PRINT 1010, (X(I), I = 1, N)

CALL SINT (N, X, WSAVE)

PRINT 1030

PRINT 1010, (X(I), I = 1, N)

C

1000 FORMAT (1X, 'Original Sequence: ')

1010 FORMAT (1X, 100(F7.3, 1X))

1020 FORMAT (1X, 'Transformed Sequence: ')

1030 FORMAT (1X, 'Recovered Sequence: ')

C

END

my_system% f95 -dalign fft_ex14.f -xlic_lib=sunperf

my_system% a.out

Original Sequence:

0.588 0.951 0.951 0.588 0.000 -0.588 -0.951 -0.951 -0.588

Transformed Sequence:

0.000 10.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000

Recovered Sequence:

11.756 19.021 19.021 11.756 0.000 -11.756 -19.021 -19.021 -11.756
Two-Dimensional FFT and Inverse Transform Routines

The following routines are used to compute a two-dimensional fast Fourier transform or inverse transform of a two-dimensional periodic sequence.

Routine Function

[R,D,C,Z]FFT2I Initialize the work array WORK for [R,D,C,Z]FFT2F or [R,D,C,Z]FFT2B

[R,D,C,Z]FFT2F Compute Fourier coefficients of two-dimensional periodic sequence

[R,D,C,Z]FFT2B Compute periodic sequence from Fourier coefficients

The xFFT2F routines compute the two-dimensional FFT by doing the following:

Perform a one-dimensional transform of the columns of the input vector.
Transpose the result matrix.
Perform a one-dimensional transform of the columns of the result matrix.
Transpose the result matrix to restore the original order of the data points.

Arguments for Two-Dimensional FFT Routines

Complex two-dimensional FFT routines use the arguments shown in TABLE 14.

TABLE 14   Arguments for Complex Two-Dimensional FFT Routines
Argument Definition

M Number of rows to be transformed

N Number of columns to be transformed

A Two-dimensional array A(LDA,N) containing the sequences to be transformed and the results of an in-place transform

LDA Leading dimension of array containing data to be transformed

WORK Work array initialized by xFFT2I

LWORK Dimension of work array WORK

Arguments for PLACE, FULL, B, and LDB are not used with the complex two-dimensional FFT routines, because the transformed sequence is stored in the original input array without any additional manipulations.

Real two-dimensional FFT routines use the arguments shown in TABLE 15.

TABLE 15   Arguments for Real Two-Dimensional FFT Routines
Argument Definition

PLACE `I' or `i' specifies that an in-place transform is performed.
`O' or `o' specifies that an out-of-place transform is performed.

FULL RFFT2F or DFFT2F only:
`F' or `f' specifies that a full result matrix is generated.
Any other character specifies that a partial result matrix is generated.

M Number of rows to be transformed

N Number of columns to be transformed

A Two-dimensional array A(LDA,N) containing the sequences to be transformed and the results of an in-place transform

LDA Leading dimension of array containing data to be transformed

B Two-dimensional array B(2*LDB,N) that stores the results of an out-of-place transform

LDB One half of the actual leading dimension of array that stores results of out-of-place transform

WORK Work array initialized by xFFT2I

LWORK Dimension of work array WORK

Normalization

The xFFT2 operations are unnormalized, so a call of xFFT2F followed by a call of xFFT2B will multiply the input sequence by M*N.

Data Storage for Two-Dimensional FFT Routines

The data storage format for the computed Fourier coefficients depends upon whether the sequence is complex or real.

Storage of Complex Two-Dimensional Sequences

When CFFT2F or ZFFT2F computes the two-dimensional FFT of a complex sequence, all Fourier coefficients are retained, and the results are stored in the original array. Additional storage options for complex two-dimensional sequences are not needed.

Storage of Real Two-Dimensional Sequences

The result of using RFFT2F or DFFT2F to compute the two-dimensional FFT of a real sequence is a complex vector that contains twice the number of values as the input sequence.

The data storage format of real two-dimensional FFT routines depends upon the following storage options.

In-place or Out-of-place. When using In-Place, the results are stored in the modified input array that contains one or two additional rows, depending upon whether M is odd or even. When using Out-of-Place, the results are stored in a separate array.
Full or Partial. When using Full, the complex conjugates are retained. When using Partial, the complex conjugates are discarded.

When computing a real one-dimensional FFT, the complex result can be packed and stored in the original array, because the values identically equal to zero and the complex conjugates are not stored. When computing the real two-dimensional FFT using the in-place and partial storage options, the complex conjugates are not stored, but the values identically equal to zero are stored. Saving the values identically equal to zero simplifies the indexing that occurs when computing the two-dimensional FFT. However, the size of the original array is modified to contain one or two additional rows, which are needed to store the values identically equal to zero.

The values of the arguments used with the real two-dimensional FFT routines depend upon whether an in-place or out-of place transform is performed, and whether the results are stored in a full or partial result matrix, as shown in TABLE 16.

TABLE 16   Relationships Between Values of Arguments for Real Two-Dimensional FFT Routines

Full Result Matrix Partial Result Matrix

In-Place Transform B unused B unused

LDB unused LDB unused

LDA must be even LDA must be even

LDA 2*M LDA M+2 if M is even
LDA M+1 if M is odd

A(1:2*M, 1:N) A(1:M+2, 1:N) if M is even
A(1:M+1, 1:N) if M is odd

Out-of-Place Transform A unchanged A unchanged

LDA M LDA M

2*LDB M 2*LDB M+2 if M is even
2*LDB M+1 if M is odd

B(1:2*M, 1:N) B(1:M+2, 1:N) if M is even
B(1:M+1, 1:N) if M is odd

When computing the real two-dimensional FFT of an input sequence of M rows and N columns, the computed Fourier coefficients will be stored in a result matrix with 2*M rows and N columns when using the Full storage option. When using the Partial storage option, the Fourier coefficients will be stored in a result matrix with M+2 rows and N columns when M is even, or in a result matrix with M+1 rows and N columns when M is odd.

For example, if M=4 and N=2, the Fourier coefficients will be stored in the output array as follows:
Full Storage Option

X(1,1) = Re(X_0) X(1,2) = Re(X_0)

X(2,1) = Im(X_0) X(2,2) = Im(X_0)

X(3,1) = Re(X_1) X(3,2) = Re(X_1)

X(4,1) = Im(X_1) X(4,2) = Im(X_1)

X(5,1) = Re(X_2) X(5,2) = Re(X_2)

X(6,1) = Im(X_2) X(6,2) = Im(X_2)

X(7,1) = Re(X_3) X(7,2) = Re(X_3)

X(8,1) = Im(X_3) X(8,2) = Im(X_3)

Partial Storage Option

X(1,1) = Re(X_0) X(1,2) = Re(X_0)

X(2,1) = Im(X_0) X(2,2) = Im(X_0)

X(3,1) = Re(X_1) X(3,2) = Re(X_1)

X(4,1) = Im(X_1) X(4,2) = Im(X_1)

X(5,1) = Re(X_2) X(5,2) = Re(X_2)

X(6,1) = Im(X_2) X(6,2) = Im(X_2)
Using Two-Dimensional FFT Routines to Perform Two-Dimensional Convolution

Sun Performance Library provides the [S,D,C,Z]CNVCOR routines for computing the convolution or correlation of a filter with one or more input vectors and the [S,D,C,Z]CNVCOR2 routines for computing the two-dimensional convolution or correlation of two matrices. These routines are described in Section Convolution and Correlation Routines. The two-dimensional FFT routines can also be used to compute the two-dimensional convolutions of the two two-dimensional arrays A and B, as described in the following procedure.

1. Compute the two-dimensional FFT of A.

2. Compute the two-dimensional FFT of B.

3. Perform pointwise multiplication of A and B.

4. Compute the inverse two-dimensional FFT of the previous result.

The second transpose can be avoided for increased performance by using the VFFT and [SDCZ]TRANS routines to explicitly compute the transposed two-dimensional FFT, as described in the following procedure.

1. Use VFFT to compute one dimensional FFTs along the columns of A.

2. Use ZTRANS to transpose A.

3. Use VFFT to compute one-dimensional FFTs along the columns of the new A.

4. Use VFFT to compute one-dimensional FFTs along the columns of B.

5. Use ZTRANS to transpose B.

6. Use VFFT to compute one-dimensional FFTs along the columns of the new B.

7. Perform pointwise multiplication of A and B.

8. Use VFFT to compute inverse one-dimensional FFTs along the columns of the result.

9. Use ZTRANS to transpose the result back into its original order.

Sample Program: Two-Dimensional FFT and Inverse Transform

CODE EXAMPLE 15 uses CFFT2F to compute the two-dimensional FFT of a two-dimensional complex sequence and CFFT2B to compute the inverse transform. The computed Fourier coefficients are stored in the original complex array. The inverse transform is unnormalized and can be normalized by dividing each value by M*N.
CODE EXAMPLE 15 Two-Dimensional FFT and Inverse of Complex Sequence

my_system: cat fft_ex15.f

PROGRAM TEST

C

INTEGER LWORK, M, N

PARAMETER (M = 2)

PARAMETER (N = 4)

PARAMETER (LWORK = 4 * (M + N + N) + 40)

INTEGER I, J

REAL PI, WORK(LWORK)

REAL X, Y

COMPLEX A(M,N)

C

EXTERNAL CFFT2B, CFFT2F, CFFT2I

INTRINSIC ACOS, CMPLX, COS, SIN

C

C Initialize the array C to a complex sequence.

C

PI = ACOS (-1.0)

DO 110, J = 1, N

DO 100, I = 1, M

X = SIN ((I - 1.0) * 2.0 * PI / N)

Y = COS ((J - 1.0) * 2.0 * PI / M)

A(I,J) = CMPLX (X, Y)

100 CONTINUE

110 CONTINUE

C

PRINT 1000

DO 200, I = 1, M

PRINT 1010, (A(I,J), J = 1, N)

200 CONTINUE

CALL CFFT2I (M, N, WORK)

CALL CFFT2F (M, N, A, M, WORK, LWORK)

PRINT 1020

DO 300, I = 1, M

PRINT 1010, (A(I,J), J = 1, N)

300 CONTINUE

CALL CFFT2B (M, N, A, M, WORK, LWORK)

PRINT 1030

DO 400, I = 1, M

PRINT 1010, (A(I,J), J = 1, N)

400 CONTINUE

C

1000 FORMAT (1X, 'Original Sequences:')

1010 FORMAT (1X, 100(F4.1,' +',F4.1,'i '))

1020 FORMAT (1X, 'Transformed Sequences:')

1030 FORMAT (1X, 'Recovered Sequences:')

C

END

my_system: f95 -dalign fft_ex15.f -xlic_lib=sunperf

my_system: a.out

Original Sequences:

0.0 + 1.0i 0.0 +-1.0i 0.0 + 1.0i 0.0 +-1.0i

1.0 + 1.0i 1.0 +-1.0i 1.0 + 1.0i 1.0 +-1.0i

Transformed Sequences:

4.0 + 0.0i 0.0 + 0.0i 0.0 + 8.0i 0.0 + 0.0i

-4.0 + 0.0i 0.0 + 0.0i 0.0 + 0.0i 0.0 + 0.0i

Recovered Sequences:

0.0 + 8.0i 0.0 +-8.0i 0.0 + 8.0i 0.0 +-8.0i

8.0 + 8.0i 8.0 +-8.0i 8.0 + 8.0i 8.0 +-8.0i
CODE EXAMPLE 15 uses RFFT2F to compute the two-dimensional FFT of a real two-dimensional sequence and RFT2B to compute the inverse transform. This example uses the FULL storage option and PLACE set to 'O' for out-of-place storage.

The computed Fourier coefficients are stored in a (2*M, N) array where one row contains the real part of the complex coefficient and the next row contains the imaginary part of the complex coefficient. In CODE EXAMPLE 15, to better display the complex conjugate symmetry, the real and imaginary parts of each complex coefficient are displayed on one line. For example, the following output:
  Transformed Out-of-Place, Full
   (   6.241,   0.000)  (   1.173,   0.000)
   (  -0.018,   1.169)  (   0.304,   0.111)
represents the following values for the Fourier coefficients.

Column 1 Column 2

Re(X₀) Im(X₀) Re(X₀) Im(X₀)

Re(X₁) Im(X₁) Re(X₁) Im(X₁)

The inverse transform is unnormalized and can be normalized by dividing each value by M*N.
CODE EXAMPLE 16 RFFT2F and RFFT2B Example Showing In-Place and Out-of-Place Storage

my_system% cat fft_ex16.f

PROGRAM TESTFFT

INTEGER M, N

PARAMETER(M = 6, N = 2)

CALL FFT(M,N)

END

SUBROUTINE FFT(M, N)

CHARACTER*1 IS_FULL

INTEGER I, J, M, N, ISTAT, LWORK, LDA, LDB, LDB_ACTUAL

REAL RNUM, RAND

EXTERNAL RFFT2F, RFFT2B, RFFT2I, RAND

REAL, DIMENSION(:,:), ALLOCATABLE :: AT, B, INPUT

REAL, DIMENSION(:), ALLOCATABLE :: WT

LDA = 2*M

LDB = 2*M

LWORK = M+2*N+MAX(M,2*N)+30

ALLOCATE(AT(LDA,N), INPUT(LDA,N), WT(LWORK), B(LDB_ACTUAL,N))

CALL RFFT2I (M, N, WT)

DO I = 1, N

DO J = 1, M

INPUT(J,I) = RAND(0)

END DO

END DO

AT = INPUT

*

PRINT *, 'Original Sequence'

DO I = 1, M

PRINT '(100(F8.3))', (AT(I,J), J = 1, N)

END DO

PRINT *

*

* Example 1

* Out-of-place, full

* leading dimension of B (2*LDB) must be at least 2*M

*

IS_FULL = 'F'

LDB = M

CALL RFFT2F ('O', IS_FULL, M, N, AT, LDA, B, LDB, WT, LWORK)

PRINT *, 'Transformed Out-of-Place, Full'

DO I = 1, LDB_ACTUAL, N

PRINT '(100('' ('', F8.3, '','', F8.3, '')'' :))',

$ (B(I,J), B(I+1,J), J = 1, N)

END DO

* B(M+3:LDB,1:N) = 0

* PRINT *, 'Transformed, last half clear:'

* DO I = 1, LDB, N

* PRINT '(100('' ('', F8.3, '','', F8.3, '')'' :))',

* $ (B(I,J), B(I+1,J), J = 1, N)

* END DO

CALL RFFT2B ('O', M, N, AT, LDA, B, LDB, WT, LWORK)

PRINT *, 'Inverse: Scaled Output, Out-of-Place, Full'

DO I = 1, M

PRINT '(100(F8.3))', (AT(I,J) / (M * N), J = 1, N)

END DO

PRINT *

*

* Example 2

* in-place, full

* LDA must be at least 2*M

*

AT = INPUT

IS_FULL = 'F'

CALL RFFT2F ('I', IS_FULL, M, N, AT, LDA, 0, 0, WT, LWORK)

PRINT *, 'Transformed In-Place, Full'

DO I = 1, LDA, 2

PRINT '(100('' ('', F8.3, '','', F8.3, '')'' :))',

$ (AT(I,J), AT(I+1,J), J = 1, N)

END DO

CALL RFFT2B ('I', M, N, AT, LDA, 0, 0, WT, LWORK)

PRINT *, 'Inverse: Scaled Output, In-Place, Full'

DO I = 1, M

PRINT '(100(F8.3))', (AT(I,J) / (M * N), J = 1, N)

END DO

PRINT *

DEALLOCATE(AT,WT,B)

END SUBROUTINE

my_system% f95 -dalign fft_ex16.f -xlic_lib=sunperf

my_system% a.out

Original Sequence

0.968 0.654

0.067 0.021

0.478 0.512

0.910 0.202

0.352 0.940

0.933 0.204

Transformed Out-of-Place, Full

( 6.241, 0.000) ( 1.173, 0.000)

( -0.018, 1.169) ( 0.304, 0.111)

( 0.981, 0.647) ( 0.945, 1.071)

( 1.569, 0.000) ( -1.790, 0.000)

( 0.981, -0.647) ( 0.945, -1.071)

( -0.018, -1.169) ( 0.304, -0.111)

Inverse: Scaled Output, Out-of-Place, Full

0.968 0.654

0.067 0.021

0.478 0.512

0.910 0.202

0.352 0.940

0.933 0.204

Transformed In-Place, Full

( 6.241, 0.000) ( 1.173, 0.000)

( -0.018, 1.169) ( 0.304, 0.111)

( 0.981, 0.647) ( 0.945, 1.071)

( 1.569, 0.000) ( -1.790, 0.000)

( 0.981, -0.647) ( 0.945, -1.071)

( -0.018, -1.169) ( 0.304, -0.111)

Inverse: Scaled Output, In-Place, Full

0.968 0.654

0.067 0.021

0.478 0.512

0.910 0.202

0.352 0.940

0.933 0.204
CODE EXAMPLE 17 is a C example that uses zfft2f to compute the two-dimensional FFT of a two-dimensional complex sequence and zfft2b to compute the inverse transform. The computed Fourier coefficients are stored in the original complex array. The inverse transform is unnormalized and can be normalized by dividing each value by m*n.
CODE EXAMPLE 17 ZFFT2F and ZFFT2B Example Using C

my_system%cat fft_ex17.c

#include <sunperf.h>

#include <math.h>

#include <stdlib.h>

/*

* This code demonstrates the use of zfft2i, zfft2f, zfft2b

*/

void

main()

{

int i,j,ip;

int m,n,max_mn;

int lwork,lda;

doublecomplex *a;

double *work;

double scale;

double err,maxerr;

m = 16; n = 8;

a = (doublecomplex *)malloc(m*n*sizeof(doublecomplex));

max_mn = m; if (n > m) max_mn = n;

lwork = 2*(m+n+max_mn)+40;

work = (double *)malloc(lwork*sizeof(double));

/* initialize a as complex(sin(i),sin(j)) */

ip = 0;

for (j=0;j<n;j++) {

for (i=0;i<m;i++) {

a[ip].r=sin((double)i);

a[ip].i=sin((double)j);

ip++;

}

}

zfft2i(m,n,work);

lda = m;

/* compute the forward fft */

zfft2f(m,n,a,lda,(doublecomplex *)&work,lwork);

/* compute the inverse fft. Note that the same work array can

be used for both the forward and the inverse fft */

zfft2b(m,n,a,lda,(doublecomplex *)&work,lwork);

/* the reconstruction result will be scaled by m*n */

scale = (double)(m*n);

maxerr = 0.0;

ip = 0;

for (j=0;j<n;j++) {

for (i=0;i<m;i++) {

err = fabs(a[ip].r/scale-sin((double)i))+
fabs(a[ip].i/scale-sin((double)j));

if (err > maxerr) maxerr = err;

ip++;

}

}

printf("reconstruction error %g \n",maxerr);

/* clean up */

free(a);

free(work);

}
CODE EXAMPLE 18 is a C example that uses rfft2f to compute the two-dimensional FFT of a two-dimensional real sequence and rfft2b to compute the inverse transform. The computed Fourier coefficients are stored in the original real array using the partial storage option. The inverse transform is unnormalized and can be normalized by dividing each value by m*n.
CODE EXAMPLE 18 Example of Using the Partial Storage Option

my_system% fft_ex18.c

#include <sunperf.h>

#include <math.h>

#include <stdlib.h>

/*

This code demonstrates the use of dfft2i, dfft2f

a is being initialized as a 2D real array of size

m x n = 8 x 4:

a =

0.700000 1.375463 -0.296165 1.493668

0.995520 1.127380 -0.225815 1.638000

1.264642 0.841120 -0.072764 1.698543

1.483327 0.542254 0.149314 1.669890

1.632039 0.257480 0.420585 1.554599

1.697495 0.012234 0.716814 1.362969

1.673848 -0.171576 1.011541 1.112118

1.563209 -0.277530 1.278440 0.824454

The 2D FFT of a is:

A =

Columns 0 through 2:

29.05310 + 0.00000i 8.02813 + 7.64742i -1.06904 + 0.00000i

-1.09423 - 0.24829i -1.78923 - 3.37830i -2.81937 + 7.27093i

-0.21980 - 0.09124i -0.16036 - 1.30903i -2.62181 + 2.67179i

-0.08924 - 0.03707i 0.20683 - 0.80372i -2.59231 + 1.08567i

-0.06281 + 0.00000i 0.38653 - 0.53453i -2.58634 + 0.00000i

-0.08924 + 0.03707i 0.50611 - 0.32973i -2.59231 - 1.08567i

-0.21980 + 0.09124i 0.57617 - 0.14256i -2.62181 - 2.67179i

-1.09423 + 0.24829i 0.21514 - 0.20391i -2.81937 - 7.27093i

Column 3:

8.02813 - 7.64742i

0.21514 + 0.20391i

0.57617 + 0.14256i

0.50611 + 0.32973i

0.38653 + 0.53453i

0.20683 + 0.80372i

-0.16036 + 1.30903i

-1.78923 + 3.37830i

To use dfft2f with the 'in-place' and 'partial storage' options,

a has to be embedded into an (m+2) x n = 10 x 8 real array (case

m even). After calling dfft2f, this array contains the (m/2+1) x n =

5 x 4 upper half of the complex result (the lower part can be determined

via the conjugate symmetry property of the result along the first

dimension.

The result of dfft2f will be:

A(0:4,:) =

Columns 0 through 2:

29.05310 + 0.00000i 8.02813 + 7.64742i -1.06904 + 0.00000i

-1.09423 - 0.24829i -1.78923 - 3.37830i -2.81937 + 7.27093i

-0.21980 - 0.09124i -0.16036 - 1.30903i -2.62181 + 2.67179i

-0.08924 - 0.03707i 0.20683 - 0.80372i -2.59231 + 1.08567i

-0.06281 + 0.00000i 0.38653 - 0.53453i -2.58634 + 0.00000i

Column 3:

8.02813 - 7.64742i

0.21514 + 0.20391i

0.57617 + 0.14256i

0.50611 + 0.32973i

0.38653 + 0.53453i

This result is stored in the original real array, i.e. a(0,0) contains

29.05310, a(1,0) contains 0.00000, a(2,0) contains -1.09423 etc.

*/

void

main()

{

int i,j,ipa;

int ip;

int m,n,max_m2n,max_mn;

int lwork,lda;

double *a;

double *work_a;

char place,full;

m = 8; n = 4;

lda = m+2;

a = (double *)malloc(lda*n*sizeof(double));

max_m2n = m; if (2*n > m) max_m2n = 2*n;

lwork = 2*(m+n+max_m2n)+30;

work_a = (double *)malloc(lwork*sizeof(double));

/* initialize a */

ipa = 0;

ip = 0;

for (j=0;j<n;j++) {

for (i=0;i<m;i++) {

a[ipa]=sin(.3*ip)+.7;

ipa++;

ip++;

}

ipa+=2;

}

dfft2i(m,n,work_a);

full = 'N';

place = 'I';

dfft2f(place,full,m,n,a,lda,NULL,0,work_a,lwork);

/* clean up */

free¹);

free(work_a);

}
Three-Dimensional FFT and Inverse Transform Routines

The following routines are used to perform a three-dimensional fast Fourier transform or inverse transform of a three-dimensional periodic sequence.

Routine Function

[R,D,C,Z]FFT3I Initialize the work array WORK for [R,D,C,Z]FFT3F or [R,D,C,Z]FFT3B

[R,D,C,Z]FFT3F Compute Fourier coefficients of three-dimensional periodic sequence

[R,D,C,Z]FFT3B Compute periodic sequence from Fourier coefficients

The xFFT3F routines compute the three-dimensional FFT by doing the following:

Perform a one-dimensional transform of the columns of the input vector.
Transpose the result matrix.
Perform a one-dimensional transform of the columns of the result matrix.
Reflect the result matrix so that the planes become columns.
Perform a one-dimensional transform of the columns of the result matrix.
Reflect and transpose the result matrix to restore the original order of the data points.

Arguments for Three-Dimensional FFT Routines

Complex three-dimensional FFT routines use the arguments shown in TABLE 17.

TABLE 17   Arguments for Complex Three-Dimensional FFT Routines
Argument Definition

M Number of rows to be transformed

N Number of columns to be transformed

K Number of planes to be transformed

A Three-dimensional array A(LDA,N,K) containing the sequences to be transformed and the results of an in-place transform

LDA Leading dimension of array containing data to be transformed, where LDA M

LD2A Second dimension of array to be transformed, where LD2A N

WORK Work array initialized by xFFT3I

LWORK Dimension of work array WORK

Arguments for PLACE, FULL, B, and LDB are not used with the complex three-dimensional FFT routines, because the transformed sequence is stored in the original input array without any additional manipulations.

Real three-dimensional FFT routines use the arguments shown in TABLE 18.

TABLE 18   Arguments for Real Three-Dimensional FFT Routines
Argument Definition

PLACE `I' or `i' specifies that an in-place transform is performed.
`O' or `o' specifies that an out-of-place transform is performed.

FULL RFFT3F or DFFT3F only:
`F' or `f' specifies that a full result matrix is generated.
Any other character specifies that a partial result matrix is generated.

M Number of rows to be transformed

N Number of columns to be transformed

K Number of planes to be transformed

A Three-dimensional array A(LDA,N,K) containing the sequences to be transformed and the results of an in-place transform

LDA Leading dimension of array containing data to be transformed

B Three-dimensional array B(2*LDB,N,K) that stores the results of an out-of-place transform

LDB Leading dimension of array that stores results of out-of-place transform

WORK Work array initialized by xFFT3I

LWORK Dimension of work array WORK

Normalization

The xFFT3 operations are unnormalized, so a call of xFFT3F followed by a call of xFFT3B will multiply the input sequence by M*N*K.

Data Storage for Three-Dimensional FFT Routines

The data storage format for the computed Fourier coefficients depends upon whether the sequence is complex or real.

Storage of Complex Three-Dimensional Sequences

When CFFT3F or ZFFT3F computes the three-dimensional FFT of a complex sequence, all Fourier coefficients are retained, and the results are stored in the original three-dimensional array A(LDA, LD2A, K). Additional storage options for complex three-dimensional sequences are not required.

Storage of Real Three-Dimensional Sequences

The result of using RFFT3F or DFFT3F to compute the three-dimensional FFT of a real sequence is a complex vector that contains twice the number of values as the input sequence.

The data storage format of real three-dimensional FFT routines depends upon the following storage options.

In-place or Out-of-place. When using In-Place, the results are stored in the modified input array that contains one or two additional rows, depending upon whether M is odd or even. When using Out-of-Place, the results are stored in a separate array.
Full or Partial. When using Full, complex conjugates are retained. When using Partial, the complex conjugates are discarded.

When computing a real one-dimensional FFT, the complex result can be packed and stored in the original array, because the values identically equal to zero and the complex conjugates are not stored. When computing the real three-dimensional FFT using the in-place and partial storage options, the complex conjugates are not stored, but the values identically equal to zero are stored. Saving the values identically equal to zero simplifies the indexing that occurs when computing the three-dimensional FFT. However, the size of the original array is modified to contain one or two additional rows, which are needed to store the values identically equal to zero.

The values of the arguments used with the real three-dimensional FFT routines depend upon whether an in-place or out-of place transform is performed, and whether the results are stored in a full or partial result matrix, as shown in TABLE 19.

TABLE 19   Relationship Between Values of Arguments for Real Three-Dimensional FFT Routines

Full Result Array Partial Result Array

In-Place Transform B unused B unused

LDB unused LDB unused

LDA must be even LDA must be even

LDA 2*M LDA M+2 if M is even
LDA M+1 if M is odd

A(1:2*M, 1:N) A(1:M+2, 1:N) if M is even
A(1:M+1, 1:N) if M is odd

Out-of-Place Transform A unchanged A unchanged

LDA M LDA M

LDB 2*M LDB M/2+1 if M is even
LDB (M-1)/2+1 if M is odd

B(1:2*M, 1:N, 1:K) B(1:M+2, 1:N, 1:K) if M is even
B(1:M+1, 1:N, 1:K) if M is odd

When computing the real 3D FFT of an input sequence of M rows, N columns, and K planes, the computed Fourier coefficients will be stored in a result matrix with 2*M rows, N columns for each value of K when using the Full storage option. When using the Partial storage option, the Fourier coefficients will be stored in a result matrix with M+2 rows and N columns for each value of K when M is even, or in M+1 rows and N columns when M is odd. For each value of K, the storage format of the Fourier coefficients in the M rows and N columns is the same as for the real two-dimensional FFT routines. See Storage of Real Two-Dimensional Sequences.

Sample Program: Three-Dimensional FFT and Inverse Transform

CODE EXAMPLE 19 uses CFFT3F to compute the three-dimensional FFT of a three-dimensional complex sequence and CFFT3B to compute the inverse transform. The computed Fourier coefficients are stored in the original complex array. The inverse transform is unnormalized and can be normalized by dividing each value by M*N*K.
CODE EXAMPLE 19 Three-Dimensional Fast Fourier Transform and Inverse Transform

my_system% cat fft_ex19.f

PROGRAM TEST

INTEGER LWORK, M, N, K

PARAMETER (K = 2)

PARAMETER (M = 2)

PARAMETER (N = 4)

PARAMETER (LWORK = 4 * (M + N + N) + 45)

C

INTEGER I, J, L

REAL PI, WORK(LWORK)

REAL X, Y

COMPLEX C(M,N,K)

C

EXTERNAL CFFT3B, CFFT3F, CFFT3I

INTRINSIC ACOS, CMPLX, COS, SIN

C Initialize the array C to a complex sequence.

PI = ACOS (-1.0)

DO 120, L = 1, K

DO 110, J = 1, N

DO 100, I = 1, M

X = SIN ((I - 1.0) * 2.0 * PI / N)

Y = COS ((J - 1.0) * 2.0 * PI / M)

C(I,J,L) = CMPLX (X, Y)

100 CONTINUE

110 CONTINUE

120 CONTINUE

C

PRINT 1000

DO 210, L = 1, K

PRINT 1010, L

DO 200, I = 1, M

PRINT 1020, (C(I,J,L), J = 1, N)

200 CONTINUE

210 CONTINUE

CALL CFFT3I (M, N, K, WORK)

CALL CFFT3F (M, N, K, C, M, N, WORK, LWORK)

PRINT 1030

DO 310, L = 1, K

PRINT 1010, L

DO 300, I = 1, M

PRINT 1020, (C(I,J,L), J = 1, N)

300 CONTINUE

310 CONTINUE

CALL CFFT3B (M, N, K, C, M, N, WORK, LWORK)

PRINT 1040

DO 410, L = 1, K

PRINT 1010, L

DO 400, I = 1, M

PRINT 1020, (C(I,J,L), J = 1, N)

400 CONTINUE

410 CONTINUE

C

1000 FORMAT (1X, 'Original Sequences:')

1010 FORMAT (1X, ' Plane', I2)

1020 FORMAT (5X, 100(F5.1,' +',F5.1,'i '))

1030 FORMAT (/1X, 'Transformed Sequences:')

1040 FORMAT (/1X, 'Recovered Sequences:')

C

END

my_system% f95 -dalign fft_ex19.f -xlic_lib=sunperf

my_system% a.out

Original Sequences:

Plane 1

0.0 + 1.0i 0.0 + -1.0i 0.0 + 1.0i 0.0 + -1.0i

1.0 + 1.0i 1.0 + -1.0i 1.0 + 1.0i 1.0 + -1.0i

Plane 2

0.0 + 1.0i 0.0 + -1.0i 0.0 + 1.0i 0.0 + -1.0i

1.0 + 1.0i 1.0 + -1.0i 1.0 + 1.0i 1.0 + -1.0i

Transformed Sequences:

Plane 1

8.0 + 0.0i 0.0 + 0.0i 0.0 + 16.0i 0.0 + 0.0i

-8.0 + 0.0i 0.0 + 0.0i 0.0 + 0.0i 0.0 + 0.0i

Plane 2

0.0 + 0.0i 0.0 + 0.0i 0.0 + 0.0i 0.0 + 0.0i

0.0 + 0.0i 0.0 + 0.0i 0.0 + 0.0i 0.0 + 0.0i

Recovered Sequences:

Plane 1

0.0 + 16.0i 0.0 +-16.0i 0.0 + 16.0i 0.0 +-16.0i

16.0 + 16.0i 16.0 +-16.0i 16.0 + 16.0i 16.0 +-16.0i

Plane 2

0.0 + 16.0i 0.0 +-16.0i 0.0 + 16.0i 0.0 +-16.0i

16.0 + 16.0i 16.0 +-16.0i 16.0 + 16.0i 16.0 +-16.0i
Convolution and Correlation Routines

The [S,D,C,Z]CNVCOR routines are used to compute the convolution or correlation of a filter with one or more input vectors. The [S,D,C,Z]CNVCOR2 routines are used to compute the two-dimensional convolution or correlation of two matrices.

Arguments for Convolution and Correlation Routines

The one-dimensional convolution and correlation routines use the arguments shown in TABLE 20.

TABLE 20   Arguments for One-Dimensional Convolution and Correlation Routines SCNVCOR, DCNVCOR, CCNVCOR, and ZCNVCOR
Argument Definition

CNVCOR `V' or `v' specifies that convolution is computed.
`R' or `r' specifies that correlation is computed.

FOUR `T' or `t' specifies that the Fourier transform method is used.
`D' or `d' specifies that the direct method is used, where the convolution or correlation is computed from the definition of convolution and correlation. (See Note 1)

NX Length of filter vector, where NX 0.

X Filter vector

IFX Index of first element of X, where NX IFX 1

INCX Stride between elements of the vector in X, where INCX > 0.

NY Length of input vectors, where NY 0.

NPRE Number of implicit zeros prefixed to the Y vectors, where NPRE 0.

M Number of input vectors, where M 0.

Y Input vectors.

IFY Index of the first element of Y, where NY IFY 1

INC1Y Stride between elements of the input vectors in Y, where INC1Y > 0.

INC2Y Stride between input vectors in Y, where INC2Y > 0.

NZ Length of the output vectors, where NZ 0.

K Number of Z vectors, where K 0. If K < M, only the first K vectors will be processed. If K > M, all input vectors will be processed and the last M-K output vectors will be set to zero on exit.

Z Result vectors

IFZ Index of the first element of Z, where NZ IFZ 1

INC1Z Stride between elements of the output vectors in Z, where INCYZ > 0.

INC2Z Stride between output vectors in Z, where INC2Z > 0.

WORK Work array

LWORK Length of work array

Note 1. When the lengths of the two sequences to be convolved are similar, the FFT method is faster than the direct method. However, when one sequence is much larger than the other, such as when convolving a large time-series signal with a small filter, the direct method performs faster than the FFT-based method.

The two-dimensional convolution and correlation routines use the arguments shown in TABLE 21.

TABLE 21   Arguments for Two-Dimensional Convolution and Correlation Routines SCNVCOR2, DCNVCOR2, CCNVCOR2, and ZCNVCOR2
Argument Definition

CNVCOR `V' or `v' specifies that convolution is computed.
`R' or `r' specifies that correlation is computed.

METHOD `T' or `t' specifies that the Fourier transform method is used.
`D' or `d' specifies that the direct method is used, where the convolution or correlation is computed from the definition of convolution and correlation. (See Note 1)

TRANSX `N' or `n' specifies that X is the filter matrix
`T' or `t' specifies that the transpose of X is the filter matrix

SCRATCHX `N' or `n' specifies that X must be preserved
`S' or `s' specifies that X can be used for scratch space. The contents of X are undefined after returning from a call where X is used for scratch space.

TRANSY `N' or `n' specifies that Y is the input matrix
`T' or `t' specifies that the transpose of Y is the input matrix

SCRATCHY `N' or `n' specifies that Y must be preserved
`S' or `s' specifies that Y can be used for scratch space. The contents of X are undefined after returning from a call where Y is used for scratch space.

MX Number of rows in the filter matrix X, where MX 0

NX Number of columns in the filter matrix X, where NX 0

X Filter matrix. X is unchanged on exit when SCRATCHX is `N' or `n' and undefined on exit when SCRATCHX is `S' or `s'.

LDX Leading dimension of array containing the filter matrix X.

MY Number of rows in the input matrix Y, where MY 0.

NY Number of columns in the input matrix Y, where NY 0

MPRE Number of implicit zeros prefixed to each row of the input matrix Y vectors, where MPRE 0.

NPRE Number of implicit zeros prefixed to each column of the input matrix Y, where NPRE 0.

Y Input matrix. Y is unchanged on exit when SCRATCHY is `N' or `n' and undefined on exit when SCRATCHY is `S' or `s'.

LDY Leading dimension of array containing the input matrix Y.

MZ Number of output vectors, where MZ 0.

NZ Length of output vectors, where NZ 0.

Z Result vectors

LDZ Leading dimension of the array containing the result matrix Z, where LDZ MAX(1,MZ).

WORKIN Work array

LWORK Length of work array

Note 1. When the sizes of the two matrices to be convolved are similar, the FFT method is faster than the direct method. However, when one sequence is much larger than the other, such as when convolving a large data set with a small filter, the direct method performs faster than the FFT-based method.

Work Array WORK for Convolution and Correlation Routines

The minimum dimensions for the WORK work arrays used with the one-dimensional and two-dimensional convolution and correlation routines are shown in TABLE 24. The minimum dimensions for one-dimensional convolution and correlation routines depend upon the values of the arguments NPRE, NX, NY, and NZ.

The minimum dimensions for two-dimensional convolution and correlation routines depend upon the values of the arguments shown TABLE 22.

TABLE 22   Arguments Affecting Minimum Work Array Size for Two-Dimensional Routines: SCNVCOR2, DCNVCOR2, CCNVCOR2, and ZCNVCOR2
Argument Definition

MX Number of rows in the filter matrix

MY Number of rows in the input matrix

MZ Number of output vectors

NX Number of columns in the filter matrix

NY Number of columns in the input matrix

NZ Length of output vectors

MPRE Number of implicit zeros prefixed to each row of the input matrix

NPRE Number of implicit zeros prefixed to each column of the input matrix

MPOST MAX(0,MZ-MYC)

NPOST MAX(0,NZ-NYC)

MYC MPRE + MPOST + MYC_INIT, where MYC_INIT depends upon filter and input matrices, as shown in TABLE 23

NYC NPRE + NPOST + NYC_INIT, where NYC_INIT depends upon filter and input matrices, as shown in TABLE 23

MYC_INIT and NYC_INIT depend upon the following, where X is the filter matrix and Y is the input matrix.

TABLE 23   MYC_INIT and NYC_INIT Dependencies

Y Transpose(Y)

X Transpose(X) X Transpose(X)

MYC_INIT MAX(MX,MY) MAX(NX,MY) MAX(MX,NY) MAX(NX,NY)

NYC_INIT MAX(NX,NY) MAX(MX,NY) MAX(NX,MY) MAX(MX,MY)

The values assigned to the minimum work array size is shown in TABLE 24.

TABLE 24   Minimum Dimensions and Data Types for WORK Work array Used With Convolution and Correlation Routines
Routine Minimum Work Array Size (WORK) Type

SCNVCOR, DCNVCOR 4*(MAX(NX,NPRE+NY) + MAX(0,NZ-NY)) REAL, REAL*8

CCNVCOR, ZCNVCOR 2*(MAX(NX,NPRE+NY) + MAX(0,NZ-NY))) COMPLEX, COMPLEX*16

SCNVCOR2^¹, DCNVCOR2¹ MY + NY + 30 COMPLEX, COMPLEX*16

CCNVCOR2¹, ZCNVCOR2¹ If MY = NY:MYC + 8If MY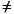 NY: MYC + NYC + 16 COMPLEX, COMPLEX*16

¹ Memory will be allocated within the routine if the workspace size, indicated by LWORK, is not large enough.

Sample Program: Convolution

CODE EXAMPLE 20 uses CCNVCOR to perform FFT convolution of two complex vectors.
CODE EXAMPLE 20 One-Dimensional Convolution Using Fourier Transform Method and COMPLEX Data

my_system% cat con_ex20.f

PROGRAM TEST

C

INTEGER LWORK

INTEGER N

PARAMETER (N = 3)

PARAMETER (LWORK = 4 * N + 15)

C

COMPLEX P1(N), P2(N), P3(2*N-1), WORK(LWORK)

C

DATA P1 / 1, 2, 3 /, P2 / 4, 5, 6 /

C

EXTERNAL CCNVCOR

C

PRINT *, 'P1:'

PRINT 1000, P1

PRINT *, 'P2:'

PRINT 1000, P2

C

CALL CCNVCOR ('V', 'T', N, P1, 1, 1, N, 0, 1, P2, 1, 1, 1,

$ 2 * N - 1, 1, P3, 1, 1, 1, WORK, LWORK)

C

PRINT *, 'P3:'

PRINT 1000, P3

C

1000 FORMAT (1X, 100(F4.1,' +',F4.1,'i '))

C

END

my_system% f95 -dalign con_ex20.f -xlic_lib=sunperf

my_system% a.out

P1:

1.0 + 0.0i 2.0 + 0.0i 3.0 + 0.0i

P2:

4.0 + 0.0i 5.0 + 0.0i 6.0 + 0.0i

P3:

4.0 + 0.0i 13.0 + 0.0i 28.0 + 0.0i 27.0 + 0.0i 18.0 + 0.0i
If any vector overlaps a writable vector, either because of argument aliasing or ill-chosen values of the various INC arguments, the results are undefined and can vary from one run to the next.

The most common form of the computation, and the case that executes fastest, is applying a filter vector X to a series of vectors stored in the columns of Y with the result placed into the columns of Z. In that case, INCX = 1, INC1Y = 1, INC2Y NY, INC1Z = 1, INC2Z NZ. Another common form is applying a filter vector X to a series of vectors stored in the rows of Y and store the result in the row of Z, in which case INCX = 1, INC1Y NY, INC2Y = 1, INC1Z NZ, and INC2Z = 1.

Convolution can be used to compute the products of polynomials. CODE EXAMPLE 21 uses SCNVCOR to compute the product of 1 + 2x + 3x² and 4 + 5x + 6x².
CODE EXAMPLE 21 One-Dimensional Convolution Using Fourier Transform Method and REAL Data

my_system% cat con_ex21.f

PROGRAM TEST

C

INTEGER LWORK, NX, NY, NZ

PARAMETER (NX = 3)

PARAMETER (NY = NX)

PARAMETER (NZ = 2*NY-1)

PARAMETER (LWORK = 4*NZ+32)

REAL X(NX), Y(NY), Z(NZ), WORK(LWORK)

C

DATA X / 1, 2, 3 /, Y / 4, 5, 6 /, WORK / LWORK*0 /

C

PRINT 1000, 'X'

PRINT 1010, X

PRINT 1000, 'Y'

PRINT 1010, Y

CALL SCNVCOR ('V', 'T', NX, X, 1, 1,

$NY, 0, 1, Y, 1, 1, 1, NZ, 1, Z, 1, 1, 1, WORK, LWORK)

PRINT 1020, 'Z'

PRINT 1010, Z

C

1000 FORMAT (1X, 'Input vector ', A1)

1010 FORMAT (1X, 300F5.0)

1020 FORMAT (1X, 'Output vector ', A1)

END

my_system% f95 -dalign con_ex21.f -xlic_lib=sunperf

my_system% a.out

Input vector X

1. 2. 3.

Input vector Y

4. 5. 6.

Output vector Z

4. 13. 28. 27. 18.
Making the output vector longer than the input vectors, as in the example above, implicitly adds zeros to the end of the input. No zeros are actually required in any of the vectors, and none are used in the example, but the padding provided by the implied zeros has the effect of an end-off shift rather than an end-around shift of the input vectors.

CODE EXAMPLE 22 will compute the product between the vector [ 1, 2, 3 ] and the circulant matrix defined by the initial column vector [ 4, 5, 6 ]:
CODE EXAMPLE 22 Convolution Used to Compute the Product of a Vector and Circulant Matrix

my_system% cat con_ex22.f

PROGRAM TEST

C

INTEGER LWORK, NX, NY, NZ

PARAMETER (NX = 3)

PARAMETER (NY = NX)

PARAMETER (NZ = NY)

PARAMETER (LWORK = 4*NZ+32)

C

REAL X(NX), Y(NY), Z(NZ), WORK(LWORK)

C

DATA X / 1, 2, 3 /, Y / 4, 5, 6 /, WORK / LWORK*0 /

C

PRINT 1000, 'X'

PRINT 1010, X

PRINT 1000, 'Y'

PRINT 1010, Y

CALL SCNVCOR ('V', 'T', NX, X, 1, 1,

$NY, 0, 1, Y, 1, 1, 1, NZ, 1, Z, 1, 1, 1,

$WORK, LWORK)

PRINT 1020, 'Z'

PRINT 1010, Z

C

1000 FORMAT (1X, 'Input vector ', A1)

1010 FORMAT (1X, 300F5.0)

1020 FORMAT (1X, 'Output vector ', A1)

C

END

my_system% f95 -dalign con_ex22.f -xlic_lib=sunperf

my_system% a.out

Input vector X

1. 2. 3.

Input vector Y

4. 5. 6.

Output vector Z

31. 31. 28.
The difference between this example and the previous example is that the length of the output vector is the same as the length of the input vectors, so there are no implied zeros on the end of the input vectors. With no implied zeros to shift into, the effect of an end-off shift from the previous example does not occur and the end-around shift results in a circulant matrix product.
CODE EXAMPLE 23 Two-Dimensional Convolution Using Direct Method

my_system% cat con_ex23.f

PROGRAM TEST

C

INTEGER M, N

PARAMETER (M = 2)

PARAMETER (N = 3)

C

INTEGER I, J

COMPLEX P1(M,N), P2(M,N), P3(M,N)

DATA P1 / 1, -2, 3, -4, 5, -6 /, P2 / -1, 2, -3, 4, -5, 6 /

EXTERNAL CCNVCOR2

C

PRINT *, 'P1:'

PRINT 1000, ((P1(I,J), J = 1, N), I = 1, M)

PRINT *, 'P2:'

PRINT 1000, ((P2(I,J), J = 1, N), I = 1, M)

C

CALL CCNVCOR2 ('V', 'Direct', 'No Transpose X', 'No Overwrite X',

$ 'No Transpose Y', 'No Overwrite Y', M, N, P1, M,

$ M, N, 0, 0, P2, M, M, N, P3, M, 0, 0)

C

PRINT *, 'P3:'

PRINT 1000, ((P3(I,J), J = 1, N), I = 1, M)

C

1000 FORMAT (3(F5.1,' +',F5.1,'i '))

C

END

my_system% f95 -dalign con_ex23.f -xlic_lib=sunperf

my_system% a.out

P1:

1.0 + 0.0i 3.0 + 0.0i 5.0 + 0.0i

-2.0 + 0.0i -4.0 + 0.0i -6.0 + 0.0i

P2:

-1.0 + 0.0i -3.0 + 0.0i -5.0 + 0.0i

2.0 + 0.0i 4.0 + 0.0i 6.0 + 0.0i

P3:

-83.0 + 0.0i -83.0 + 0.0i -59.0 + 0.0i

80.0 + 0.0i 80.0 + 0.0i 56.0 + 0.0i
References

For additional information on the DFT or FFT, see the following sources.

Briggs, William L., and Henson, Van Emden. The DFT: An Owner's Manual for the Discrete Fourier Transform. Philadelphia, PA: SIAM, 1995.

Brigham, E. Oran. The Fast Fourier Transform and Its Applications. Upper Saddle River, NJ: Prentice Hall, 1988.

Chu, Eleanor, and George, Alan. Inside the FFT Black Box: Serial and Parallel Fast Fourier Transform Algorithms. Boca Raton, FL: CRC Press, 2000.

Press, William H., Teukolsky, Saul A., Vetterling, William T., and Flannery, Brian P. Numerical Recipes in C: The Art of Scientific Computing. 2 ed. Cambridge, United Kingdom: Cambridge University Press, 1992.

Ramirez, Robert W. The FFT: Fundamentals and Concepts. Englewood Cliffs, NJ: Prentice-Hall, Inc., 1985.

Rodrigue, Garry ed. Parallel Computations. New York: Academic Press, Inc., 1982.

Strang, Gilbert. Linear Algebra and Its Applications. 3 ed. Orlando, FL: Harcourt Brace & Company, 1988.

Van Loan, Charles. Computational Frameworks for the Fast Fourier Transform. Philadelphia, PA: SIAM, 1992.

Walker, James S. Fast Fourier Transforms. Boca Raton, FL: CRC Press, 1991.

**TABLE 1** Comparison Between Single Vector and Multiple Vector Routines
	Single Vector	Multiple Vector
One-Dimensional Routines
Input	Vector of length N	An array of vectors
Output	Single transform or inverse transform	Multiple transforms or inverse transform (one transform or inverse transform per sequence)
Results	Unnormalized^¹	Normalized
Two-Dimensional Routines
Input	Two-dimensional array	Multiple vector two-dimensional routines are not supported
Output	Two-dimensional transform or inverse transform
Results	Unnormalized
Three-Dimensional Routines
Input	Three-dimensional array	Multiple vector three-dimensional routines are not supported
Output	Three-dimensional transform or inverse transform
Results	Unnormalized

**TABLE 2** Formulas for Real FFT Routines
	Transform
Odd N	,
Even N
	Inverse Transform
Odd N
Even N	,

**TABLE 3** Symmetries Supported by FFT and VFFT Routines
Symmetry	Definition	Trigonometric Expansion
Cosine Even-Wave	An even function f(t) that satisfies the condition f(-t) = f(t).	Trigonometric series containing only cosine terms.
Cosine Quarter-Wave	A even function with half-wave symmetry , where T is the period of the function.	Trigonometric series containing only cosine terms with odd wave numbers.
Sine Odd-Wave	An odd function f(t) that satisfies the condition f(-t) =-f(t).	Trigonometric series containing only sine terms.
Sine Quarter-Wave	A odd function with half-wave symmetry .	Trigonometric series containing only sine terms with odd wave numbers.

**TABLE 4** Formulas for Symmetries Supported by FFT and VFFT Routines
	Cosine Even-Wave^¹
Transform/ Inverse Transform	,
	Cosine Quarter-Wave
Transform	,
Inverse Transform	,
	Sine Odd-Wave¹
Transform/ Inverse Transform	,
	Sine Quarter-Wave
Transform	,
Inverse Transform	,

**TABLE 5** Prefix and Operand Data Types
	Prefix	Operand Data Type
FFT Routines	No prefix	`REAL`, `REAL*4`, `REAL(4)`
	`R`	`REAL`, `REAL*4`, `REAL(4)`
	`D`	`DOUBLE`, `REAL*8`, `REAL(8)`
	`C`	`COMPLEX`, `COMPLEX*8`, `COMPLEX(4)`
	`Z`	`DOUBLE` `COMPLEX`, `COMPLEX*16`, `COMPLEX(8)`
VFFT Routines	`VR`	`REAL`, `REAL*4`, `REAL(4)`
	`VD`	`DOUBLE`, `REAL*8`, `REAL(8)`
	`VC`	`COMPLEX`, `COMPLEX*8`, `COMPLEX(4)`
	`VZ`	`DOUBLE` `COMPLEX`, `COMPLEX*16`, `COMPLEX(8)`

**TABLE 6** FFT and VFFT Base Names
Base Name	Operation
`COSQB`	Inverse cosine quarter-wave transform (synthesis)
`COSQF`	Cosine quarter-wave transform
`COSQI`	Initialize cosine quarter-wave transform or inverse transform
`COST`	Cosine even-wave transform
`COSTI`	Initialize cosine even-wave transform
`EZFFTB`	Inverse EZ transform (synthesis)
`EZFFTF`	EZ transform
`EZFFTI`	Initialize EZ transform
`FFTB`	Inverse transform (synthesis)
`FFTF`	Forward transform
`FFTI`	Initialize before computing a transform or inverse transform
`SINQB`	Inverse sine quarter-wave transform (synthesis)
`SINQF`	Sine quarter-wave transform
`SINQI`	Initialize sine quarter-wave transform or inverse transform
`SINT`	Sine odd-wave transform
`SINTI`	Initialize sine odd-wave transform

Convention	Routines
x`FFTF`	`RFFTF`, `DFFTF`, `CFFTF`, and `ZFFTF`
`[R,D]FFTI`	`RFFTI` or `DFFTI`
`[C,Z]FFTF`	`CFFTF` or `ZFFTF`
`V[R,D,C,Z]FFTF`	`VRFFTF`, `VDFFTF`, `VCFFTF`, or `VZFFTF`

**TABLE 7** Argument Data Types
Argument	Data Type
`AZERO`, `A`, `B`, `R` (EZFFT routines)	Real
`FULL`, `PLACE`, `ROWCOL`	Character
`N`, `M`, `K`, `LDA`, `LD2A`, `LDB`, `LWORK`, `MDIMX`	Integer
`A`, `B`, `X`, `XT`	Same as data type of routine called
`WSAVE`, `WORK`	See TABLE 11

**TABLE 8** FFT Routines
Routine	Arguments	Function
`COSQB`, `DCOSQB`	`N,X,WSAVE`	Inverse cosine quarter-wave transform
`VCOSQB`, `VDCOSQB`	`M,N,X,XT,MDIMX,WSAVE`	Inverse cosine quarter-wave transform (Vector)
`COSQF`, `DCOSQF`	`N,X,WSAVE`	Cosine quarter-wave transform
`VCOSQF`, `VDCOSQF`	`M,N,X,XT,MDIMX,WSAVE`	Cosine quarter-wave transform (Vector)
`COSQI`, `DCOSQI`	`N,WSAVE`	Initialize cosine quarter-wave transform and inverse transform
`VCOSQI`, `VDCOSQI`	`N,WSAVE`	Initialize cosine quarter-wave transform and inverse transform (Vector)
`COST`, `DCOST`	`N,X,WSAVE`	Cosine even-wave transform
`VCOST`, `VDCOST`	`M,N,X,XT,MDIMX,WSAVE`	Cosine even-wave transform (Vector)
`COSTI`, `DCOSTI`	`N,WSAVE`	Initialize cosine even-wave transform
`VCOSTI`, `VDCOSTI`	`N,WSAVE`	Initialize cosine even-wave transform (Vector)
`EZFFTB`	`N,R,AZERO,A,B,WSAVE`	EZ inverse Fourier transform
`EZFFTF`	`N,R,AZERO,A,B,WSAVE`	EZ Fourier transform
`EZFFTI`	`N,WSAVE`	Initialize EZ Fourier transform and inverse transform
`RFFTB`, `DFFTB`, `CFFTB`, `ZFFTB`	`N,X,WSAVE`	Inverse Fourier transform
`VRFFTB`, `VDFFTB`	`M,N,X,XT,MDIMX,WSAVE`	Inverse Fourier transform (Vector)
`VCFFTB`, `VZFFTB`	`M,N,X,XT,MDIMX, ROWCOL,WSAVE`
`RFFTF`, `DFFTF`, `CFFTF`, `ZFFTF`	`N,X,WSAVE`	Fourier transform
`VRFFTF`, `VDFFTF`	`M,N,X,XT,MDIMX,WSAVE`	Fourier transform (Vector)
`VCFFTF`, `VZFFTF`	`M,N,X,XT,MDIMX, ROWCOL,WSAVE`
`RFFTI`, `DFFTI`, `CFFTI`, `ZFFTI`	`N,WSAVE`	Initialize Fourier transform and inverse transform
`VRFFTI`, `VDFFTI, VCFFTI`, `VZFFTI`	`N,WSAVE`	Initialize Fourier transform and inverse transform (Vector)
`SINQB`, `DSINQB`	`N,X,WSAVE`	Inverse sine quarter-wave transform
`VSINQB`, `VDSINQB`	`M,N,X,XT,MDIMX,WSAVE`	Inverse sine quarter-wave transform (Vector)
`SINQF`, `DSINQF`	`N,X,WSAVE`	Sine quarter-wave transform
`VSINQF`, `VDSINQF`	`M,N,X,XT,MDIMX,WSAVE`	Sine quarter-wave transform (Vector)
`SINQI`, `DSINQI`	`N,WSAVE`	Initialize sine quarter-wave transform and inverse transform
`VSINQI`, `VDSINQI`	`N,WSAVE`	Initialize sine quarter-wave transform and inverse transform (Vector)
`SINT`, `DSINT`	`N,X,WSAVE`	Sine odd-wave transform
`VSINT`, `VDSINT`	`M,N,X,XT,MDIMX,WSAVE`	Sine odd-wave transform (Vector)
`SINTI`, `DSINT`	`N,WSAVE`	Initialize sine odd-wave transform
`VSINTI`, `VDSINTI`	`N,WSAVE`	Initialize sine odd-wave transform (Vector)
`RFFT2B`, `DFFT2B`	`PLACE,M,N,A,LDA, B,LDB,WORK,LWORK`	Inverse two-dimensional Fourier transform
`CFFT2B`, `ZFFT2B`	`M,N,A,LDA,WORK,LWORK`
`RFFT2F`, `DFFT2F`	`PLACE,FULL,M,N,A,LDA, B,LDB,WORK,LWORK`	Two-dimensional Fourier transform
`CFFT2F`, `ZFFT2F`	`M,N,A,LDA,WORK,LWORK`
`RFFT2I`, `DFFT2I, CFFT2I`, `ZFFT2I`	`M,N,WORK`	Initialize two-dimensional Fourier transform and inverse transform
`RFFT3B`, `DFFT3B`	`PLACE,M,N,K,A,LDA, B,LDB,WORK,LWORK`	Inverse three-dimensional Fourier transform
`CFFT3B`, `ZFFT3B`	`M,N,K,A,LDA,LD2A, WORK,LWORK`
`RFFT3F`, `DFFT3F`	`PLACE,FULL,M,N,K, A,LDA,B,LDB,WORK,LWORK`	Three-dimensional Fourier transform
`CFFT3F`, `ZFFT3F`	`M,N,K,A,LDA,LD2A, WORK,LWORK`
`RFFT3I`, `DFFT3I, CFFT3I`, `ZFFT3I`	`M,N,K,WORK`	Initialize three-dimensional Fourier transform and inverse transform

**TABLE 9** Convolution and Correlation Routines
Routine	Arguments	Function
`SCNVCOR`, `DCNVCOR`, `CCNVCOR`, `ZCNVCOR`	`CNVCOR,FOUR,NX,X,IFX, INCX,NY,NPRE,M,Y,IFY, INC1Y,INC2Y,NZ,K,Z, IFZ,INC1Z,INC2Z,WORK, LWORK`	Convolution or correlation of two vectors
`SCNVCOR2`, `DCNVCOR2`, `CCNVCOR2`, `ZCNVCOR2`	`CNVCOR,METHOD,TRANSX, SCRATCHX,TRANSY, SCRATCHY,MX,NX,X,LDX, MY,NY,MPRE,NPRE,Y,LDY, MZ,NZ,Z,LDZ,WORKIN, LWORK`	Convolution or correlation of two matrices

**TABLE 10** Values That Must Have 2, 3, 4, 5, 7, 11, or 13 as Factors for Best Performance
Routine	Values
`COST`, `DCOST`, `VCOST,` `VDCOST`	`N` `-` `1`
`SINT`, `DSINT`, `VSINT,` `VDSINT`	`N` `+` `1`
All other one-dimensional FFT and VFFT routines	`N`
Two-dimensional FFT routines	`M` and `N`
Three-dimensional FFT routines	`M`, `N`, and `K`

INTEGER N REAL WSAVE (2 * N + 15) CALL RFFTI (N, WSAVE)

INTEGER N REAL WSAVE (4 * N + 15) CALL CFFTI (N, WSAVE)

**TABLE 11** Minimum Dimensions and Data Types for `WSAVE` Work Array
Routine	Minimum Work Array Size (`WSAVE`)	Type
One-Dimensional Routines
`COSQI, DCOSQI`	`3N + 15`	`REAL, REAL*8`
`COSQB, DCOSQB`	`3N + 15`	`REAL, REAL*8`
`COSQF, DCOSQF`	`3N + 15`	`REAL, REAL*8`
`COST, DCOST`	`3N + 15`	`REAL, REAL*8`
`COSTI, DCOSTI`	`3N + 15`	`REAL, REAL*8`
`EZFFTB`	`3N + 15`	`REAL, REAL*8`
`EZFFTF`	`3N + 15`	`REAL, REAL*8`
`EZFFTI`	`3N + 15`	`REAL, REAL*8`
`RFFTB, DFFTB`	`2N + 15`	`REAL, REAL*8`
`RFFTF, DFFTF`	`2N + 15`	`REAL, REAL*8`
`RFFTI, DFFTI`	`2N + 15`	`REAL, REAL*8`
`CFFTB, ZFFTB`	`4N + 15`	`REAL, REAL*8`
`CFFTF, ZFFTF`	`4N + 15`	`REAL, REAL*8`
`CFFTI, ZFFTI`	`4N + 15`	`REAL, REAL*8`
`SINQB, DSINQB`	`3N + 15`	`REAL, REAL*8`
`SINQF, DSINQF`	`3N + 15`	`REAL, REAL*8`
`SINQI, DSINQI`	`3N + 15`	`REAL, REAL*8`
`SINT, DSINT`	`2N + N/2 + 15`	`REAL, REAL*8`
`SINTI, DSINTI`	`2N + N/2 + 15`	`REAL, REAL*8`
VFFT Routines
`VRFFTB, VDFFTB`	`N + 15`	`REAL, REAL*8`
`VRFFTF, VDFFTF`	`N + 15`	`REAL, REAL*8`
`VRFFTI, VDFFTI`	`N + 15`	`REAL, REAL*8`
`VCFFTB, VZFFTB`	If transforming rows: `2 * M + 15`If transforming columns: `2 * N + 15`	`REAL, REAL*8`
`VCFFTF, VZFFTF`	If transforming rows: `2 * M + 15`If transforming columns: `2 * N + 15`	`REAL, REAL*8`
`VCFFTI, VZFFTI`	`N + 15`	`REAL, REAL*8`
`VCOSQB, VDCOSQB`	`2 * N + 15`	`REAL, REAL*8`
`VCOSQF, VDCOSQF`	`2 * N + 15`	`REAL, REAL*8`
`VCOSQI, VDCOSQI`	`2 * N + 15`	`REAL, REAL*8`
`VCOST, VDCOST`	`2 * N + 15`	`REAL, REAL*8`
`VCOSTI, VDCOSTI`	`2 * N + 15`	`REAL, REAL*8`
`VSINQB, VDSINQB`	`2 * N + 15`	`REAL, REAL*8`
`VSINQF, VDSINQF`	`2 * N + 15`	`REAL, REAL*8`
`VSINQI, VDSINQI`	`2 * N + 15`	`REAL, REAL*8`
`VSINT, VDSINT`	`N + N/2 + 15`	`REAL, REAL*8`
`VSINTI, VDSINTI`	`N + N/2 + 15`	`REAL, REAL*8`
Two-Dimensional Routines
`RFFT2B, DFFT2B`	`(M + 2N + MAX(M, 2N) + 30)`	`REAL, REAL*8`
`RFFT2F, DFFT2F`	`(M + 2N + MAX(M, 2N) + 30)`	`REAL, REAL*8`
`RFFT2I, DFFT2I`	`(M + 2N + MAX(M, 2N) + 30)`	`REAL, REAL*8`
`CFFT2B, ZFFT2B`	`(4 * (M + N) + 30)`	`REAL, REAL*8`
`CFFT2F, ZFFT2F`	`(4 * (M + N) + 30)`	`REAL, REAL*8`
`CFFT2I, ZFFT2I`	`(4 * (M + N) + 30)`	`REAL, REAL*8`
Three-Dimensional Routines
`RFFT3B, DFFT3B`	`(M + 2 * (N + K) + 4K + 45)`	`REAL, REAL*8`
`RFFT3F, DFFT3F`	`(M + 2 * (N + K) + 4K + 45)`	`REAL, REAL*8`
`RFFT3I, DFFT3I`	`(M + 2 * (N + K) + 30)`	`REAL, REAL*8`
`CFFT3B, ZFFT3B`	`(4 * (M + N + K) + 45)`	`REAL, REAL*8`
`CFFT3F, ZFFT3F`	`(4 * (M + N + K) + 45)`	`REAL, REAL*8`
`CFFT3I, ZFFT3I`	`(4 * (M + N + K) + 45)`	`REAL, REAL*8`

CALL CFFTI (M, WSAVE) C$PAR DOALL SHARED(M, WSAVE, N, C), PRIVATE(I) DO I = 1, N CALL CFFTF (M, C(1, I), WSAVE) CALL CFFTB (M, C(1, I), WSAVE) END DO

**TABLE 12** Arguments for FFT and VFFT Routines
Arguments	Description
FFT Routines
`N`	Length of the sequence to be transformed, where `N` 0.
`X`	On entry, an array of length `N` containing the sequence to be transformed.
`WSAVE`	On entry, a work array with a minimum dimension that depends upon the type of routine used and the data type of the operands. See TABLE 11 for a complete list of minimum work array dimensions.
VFFT Routines
`N`	Length of the sequence to be transformed, where `N` 0.
`M`	Number of sequences to be transformed, where `M` 0.
`X`	A two-dimensional array `X(M,N)` whose rows contain the sequences to be transformed.
`XT`	A two-dimensional work array with dimensions of `(MDIMX` * `N)`.
`MDIMX`	Leading dimension of the arrays `X` and `XT` as specified in a dimension or type statement, where `MDIMX` `M`.
`WSAVE`	On entry, a work array with a minimum dimension that depends upon the type of routine used and the data type of the operands. See TABLE 11 for a complete list of minimum work array dimensions.

Routine	Function
`[R,D,C,Z]FFTI`	Initialize work array `WSAVE` for `[R,D,C,Z]FFTF` or `[R,D,C,Z]FFTB`
`[R,D,C,Z]FFTF`	Compute Fourier coefficients of periodic sequence
`[R,D,C,Z]FFTB`	Compute periodic sequence from Fourier coefficients
`V[R,D,C,Z]FFTI`	Initialize work array for `V[R,D,C,Z]FFTF` or `V[R,D,C,Z]FFTB`
`V[R,D,C,Z]FFTF`	Compute Fourier coefficients of multiple periodic sequences
`V[R,D,C,Z]FFTB`	Compute multiple periodic sequences from Fourier coefficients

Routine	Function
`EZFFTI`	Initialize work array `WSAVE` for `EZFFTF` or `EZFFTB`
`EZFFTF`	Compute Fourier coefficients of periodic sequence
`EZFFTB`	Compute periodic sequence from Fourier coefficients

**TABLE 13** Arguments for EZFFT Routines
Argument	Definition
`N`	Sequence length
`R`	For `EZFFTF`, a real array containing the sequence to be transformed, unchanged on exit. For `EZFFTB`, a real array containing the Fourier coefficients of the inputs.
`AZERO`	The Fourier constant A₀
`A`	Real array containing the real parts of the complex Fourier coefficients. If `N` is even, then `A` is length `N`/2, otherwise `A` is length (`N`-1)/2.
`B`	Real array containing the imaginary parts of the complex Fourier coefficients. If `N` is even, then `B` is length `N`/2, otherwise `B` is length (`N`-1)/2.
`WSAVE`	Work array initialized by `EZFFTI`

Routine	Function
`[D]COSQI`	Initialize work array `WSAVE` for `[D]COSQF` or `[D]COSQB`
`[D]COSQF`	Compute Fourier coefficients of cosine series with odd wave numbers
`[D]COSQB`	Compute periodic sequence from Fourier coefficients
`V[D]COSQI`	Initialize work array for `V[D]COSQF` or `V[D]COSQB`
`V[D]COSQF`	Compute Fourier coefficients of multiple cosine series with odd wave numbers
`V[D]COSQB`	Compute multiple periodic sequences from Fourier coefficients

Routine	Function
`[D]COSTI`	Initialize work array `WSAVE` for `[D]COSTF` or `[D]COSTB`
`[D]COST`	Compute the Fourier coefficients or inverse transform of an even sequence
`V[D]COSTI`	Initialize work array for `V[D]COSTF` or `V[D]COSTB`
`V[D]COST`	Compute Fourier coefficients or inverse transform of multiple even sequences

Routine	Function
`[D]SINQI`	Initialize work array `WSAVE` for `[D]SINQF` or `[D]SINQB`
`[D]SINQF`	Compute Fourier coefficients of sine series with only odd wave numbers
`[D]SINQB`	Compute periodic sequence from Fourier coefficients
`V[D]SINQI`	Initialize work array for `V[D]SINQF` or `V[D]SINQB`
`V[D]SINQF`	Compute Fourier coefficients of multiple sine series with only odd wave numbers
`V[D]SINQB`	Compute multiple periodic sequences from Fourier coefficients

Library | Contents | Previous | Next | Index

Routine	Function
`[D]SINTI`	Initialize work array `WSAVE` for `[D]SINQF` or `[D]SINQB`
`[D]SINT`	Compute the Fourier coefficients or inverse transform of a sine series with only odd wave numbers
`V[D]SINTI`	Initialize work array for `V[D]SINQF` or `V[D]SINQB`
`V[D]SINT`	Compute the Fourier coefficients or inverse transform of multiple sine series with only odd wave numbers

Routine	Function
`[R,D,C,Z]FFT2I`	Initialize the work array `WORK` for `[R,D,C,Z]FFT2F` or `[R,D,C,Z]FFT2B`
`[R,D,C,Z]FFT2F`	Compute Fourier coefficients of two-dimensional periodic sequence
`[R,D,C,Z]FFT2B`	Compute periodic sequence from Fourier coefficients

Argument	Definition
`M`	Number of rows to be transformed
`N`	Number of columns to be transformed
`A`	Two-dimensional array `A(LDA,N)` containing the sequences to be transformed and the results of an in-place transform
`LDA`	Leading dimension of array containing data to be transformed
`WORK`	Work array initialized by xFFT2I
`LWORK`	Dimension of work array `WORK`

Argument	Definition
`PLACE`	`I' or `i' specifies that an in-place transform is performed. `O' or `o' specifies that an out-of-place transform is performed.
`FULL`	`RFFT2F` or `DFFT2F` only: `F' or `f' specifies that a full result matrix is generated. Any other character specifies that a partial result matrix is generated.
`M`	Number of rows to be transformed
`N`	Number of columns to be transformed
`A`	Two-dimensional array `A(LDA,N)` containing the sequences to be transformed and the results of an in-place transform
`LDA`	Leading dimension of array containing data to be transformed
`B`	Two-dimensional array `B(2*LDB,N`) that stores the results of an out-of-place transform
`LDB`	One half of the actual leading dimension of array that stores results of out-of-place transform
`WORK`	Work array initialized by xFFT2I
`LWORK`	Dimension of work array `WORK`

	Full Result Matrix	Partial Result Matrix
In-Place Transform	`B` unused	`B` unused
	`LDB` unused	`LDB` unused
	`LDA` must be even	`LDA` must be even
	`LDA` `2*M`	`LDA` `M+2` if `M` is even `LDA` `M+1` if `M` is odd
	`A(1:2*M`, `1:N)`	`A(1:M+2,` `1:N)` if `M` is even `A(1:M+1,` `1:N)` if `M` is odd
Out-of-Place Transform	`A` unchanged	`A` unchanged
	`LDA` `M`	`LDA` `M`
	`2*LDB` `M`	`2LDB` `M+2` if `M` is even `2LDB` `M+1` if `M` is odd
	`B(1:2*M`, `1:N)`	`B(1:M+2`, `1:N)` if `M` is even `B(1:M+1`, `1:N)` if `M` is odd

Column 1		Column 2
Re(X₀)	Im(X₀)	Re(X₀)	Im(X₀)
Re(X₁)	Im(X₁)	Re(X₁)	Im(X₁)

Routine	Function
`[R,D,C,Z]FFT3I`	Initialize the work array `WORK` for `[R,D,C,Z]FFT3F` or `[R,D,C,Z]FFT3B`
`[R,D,C,Z]FFT3F`	Compute Fourier coefficients of three-dimensional periodic sequence
`[R,D,C,Z]FFT3B`	Compute periodic sequence from Fourier coefficients

Argument	Definition
`M`	Number of rows to be transformed
`N`	Number of columns to be transformed
`K`	Number of planes to be transformed
`A`	Three-dimensional array `A(LDA,N,K)` containing the sequences to be transformed and the results of an in-place transform
`LDA`	Leading dimension of array containing data to be transformed, where `LDA` `M`
`LD2A`	Second dimension of array to be transformed, where `LD2A` `N`
`WORK`	Work array initialized by xFFT3I
`LWORK`	Dimension of work array `WORK`

Argument	Definition
`CNVCOR`	`V' or `v' specifies that convolution is computed. `R' or `r' specifies that correlation is computed.
`FOUR`	`T' or `t' specifies that the Fourier transform method is used. `D' or `d' specifies that the direct method is used, where the convolution or correlation is computed from the definition of convolution and correlation. (See Note 1)
`NX`	Length of filter vector, where `NX` 0.
`X`	Filter vector
`IFX`	Index of first element of `X`, where `NX` `IFX` 1
`INCX`	Stride between elements of the vector in `X`, where `INCX` > 0.
`NY`	Length of input vectors, where `NY` 0.
`NPRE`	Number of implicit zeros prefixed to the `Y` vectors, where `NPRE` 0.
`M`	Number of input vectors, where `M` 0.
`Y`	Input vectors.
IFY	Index of the first element of `Y`, where `NY` `IFY` 1
INC1Y	Stride between elements of the input vectors in `Y`, where `INC1Y` > 0.
INC2Y	Stride between input vectors in `Y`, where `INC2Y` > 0.
NZ	Length of the output vectors, where `NZ` 0.
K	Number of `Z` vectors, where `K` 0. If `K` < `M`, only the first `K` vectors will be processed. If `K` > `M`, all input vectors will be processed and the last `M`-`K` output vectors will be set to zero on exit.
Z	Result vectors
IFZ	Index of the first element of `Z`, where `NZ` `IFZ` 1
INC1Z	Stride between elements of the output vectors in `Z`, where `INCYZ` > 0.
INC2Z	Stride between output vectors in `Z`, where `INC2Z` > 0.
WORK	Work array
LWORK	Length of work array

Argument	Definition
`CNVCOR`	`V' or `v' specifies that convolution is computed. `R' or `r' specifies that correlation is computed.
`METHOD`	`T' or `t' specifies that the Fourier transform method is used. `D' or `d' specifies that the direct method is used, where the convolution or correlation is computed from the definition of convolution and correlation. (See Note 1)
`TRANSX`	`N' or `n' specifies that `X` is the filter matrix `T' or `t' specifies that the transpose of `X` is the filter matrix
`SCRATCHX`	`N' or `n' specifies that `X` must be preserved `S' or `s' specifies that `X` can be used for scratch space. The contents of `X` are undefined after returning from a call where `X` is used for scratch space.
`TRANSY`	`N' or `n' specifies that `Y` is the input matrix `T' or `t' specifies that the transpose of `Y` is the input matrix
`SCRATCHY`	`N' or `n' specifies that `Y` must be preserved `S' or `s' specifies that `Y` can be used for scratch space. The contents of `X` are undefined after returning from a call where `Y` is used for scratch space.
`MX`	Number of rows in the filter matrix `X`, where `MX` 0
`NX`	Number of columns in the filter matrix `X`, where `NX` 0
`X`	Filter matrix. `X` is unchanged on exit when `SCRATCHX` is `N' or `n' and undefined on exit when `SCRATCHX` is `S' or `s'.
`LDX`	Leading dimension of array containing the filter matrix `X`.
`MY`	Number of rows in the input matrix `Y`, where `MY` 0.
NY	Number of columns in the input matrix `Y`, where `NY` 0
MPRE	Number of implicit zeros prefixed to each row of the input matrix `Y` vectors, where `MPRE` 0.
NPRE	Number of implicit zeros prefixed to each column of the input matrix `Y`, where `NPRE` 0.
Y	Input matrix. `Y` is unchanged on exit when `SCRATCHY` is `N' or `n' and undefined on exit when `SCRATCHY` is `S' or `s'.
LDY	Leading dimension of array containing the input matrix `Y`.
MZ	Number of output vectors, where `MZ` 0.
NZ	Length of output vectors, where `NZ` 0.
Z	Result vectors
LDZ	Leading dimension of the array containing the result matrix `Z`, where `LDZ` `MAX(1,MZ)`.
WORKIN	Work array
LWORK	Length of work array

Argument	Definition
`MX`	Number of rows in the filter matrix
`MY`	Number of rows in the input matrix
`MZ`	Number of output vectors
`NX`	Number of columns in the filter matrix
`NY`	Number of columns in the input matrix
`NZ`	Length of output vectors
`MPRE`	Number of implicit zeros prefixed to each row of the input matrix
`NPRE`	Number of implicit zeros prefixed to each column of the input matrix
`MPOST`	`MAX(0,MZ-MYC)`
`NPOST`	`MAX(0,NZ-NYC)`
`MYC`	`MPRE` + `MPOST` + `MYC_INIT`, where `MYC_INIT` depends upon filter and input matrices, as shown in TABLE 23
`NYC`	`NPRE` + `NPOST` + `NYC_INIT`, where `NYC_INIT` depends upon filter and input matrices, as shown in TABLE 23

	Y		Transpose(Y)
	X	Transpose(X)	X	Transpose(X)
`MYC_INIT`	`MAX(MX,MY)`	`MAX(NX,MY)`	`MAX(MX,NY)`	`MAX(NX,NY)`
`NYC_INIT`	`MAX(NX,NY)`	`MAX(MX,NY)`	`MAX(NX,MY)`	`MAX(MX,MY)`

Routine	Minimum Work Array Size (`WORK`)	Type
`SCNVCOR, DCNVCOR`	`4*(MAX(NX,NPRE+NY)` `+ MAX(0,NZ-NY))`	`REAL, REAL*8`
`CCNVCOR, ZCNVCOR`	`2*(MAX(NX,NPRE+NY)` `+ MAX(0,NZ-NY)))`	`COMPLEX, COMPLEX*16`
`SCNVCOR2`^¹`, DCNVCOR2`¹	`MY` `+` `NY` `+` `30`	`COMPLEX, COMPLEX*16`
`SCNVCOR2`^¹`, DCNVCOR2`¹	`MY` `+` `NY` `+` `30`	`COMPLEX, COMPLEX*16`
`CCNVCOR2`¹`, ZCNVCOR2`¹	If `MY` = `NY`:`MYC + 8`If `MY` `NY: MYC + NYC + 16`	`COMPLEX, COMPLEX*16`

Using Sun Performance Library Fast Fourier Transform Routines

Introduction to the FFTPACK and VFFTPACK Packages

Extensions to FFTPACK and VFFTPACK

The Discrete Fourier Transform (DFT)

Naming Conventions

Sun Performance Library FFT Routines

Calling FFT Routines

Fortran Interface Conventions

C Interface Conventions

Using 64-Bit FFT Routines

Sequence Length N

Work Array WSAVE for FFT and VFFT Routines

Parallelization

One-Dimensional FFT and Inverse Transform Routines

Arguments for One-Dimensional FFT and VFFT Routines

Data Storage for One-Dimensional FFT and VFFT Routines

Storage of Complex Sequences

Storage of Real Sequences

FFT: Fast Fourier Transform Routines

Normalization

Sample Programs: Fast Fourier Transform and Inverse Transform

EZFFT: EZ Fourier Transform Routines

Sample Program: EZ Fourier Transform and Inverse Transform

COSQ: Cosine Quarter-Wave Routines

Normalization

Sample Programs: Cosine Quarter-Wave Transform and Inverse Transform

COST: Cosine Even-Wave Routines

Normalization

Sample Program: Cosine Even-Wave Transform and Inverse Transform

SINQ: Sine Quarter-Wave Routines

Normalization

Sample Programs: Sine Quarter-Wave Transform and Inverse Transform

SINT: Sine Odd-Wave Transform Routines

Normalization

Sample Program: Sine Odd-Wave Transform

Two-Dimensional FFT and Inverse Transform Routines

Arguments for Two-Dimensional FFT Routines

Normalization

Data Storage for Two-Dimensional FFT Routines

Storage of Complex Two-Dimensional Sequences

Storage of Real Two-Dimensional Sequences

Using Two-Dimensional FFT Routines to Perform Two-Dimensional Convolution

Sample Program: Two-Dimensional FFT and Inverse Transform

Three-Dimensional FFT and Inverse Transform Routines

Arguments for Three-Dimensional FFT Routines

Normalization

Data Storage for Three-Dimensional FFT Routines

Storage of Complex Three-Dimensional Sequences

Storage of Real Three-Dimensional Sequences

Sample Program: Three-Dimensional FFT and Inverse Transform

Convolution and Correlation Routines

Arguments for Convolution and Correlation Routines

Work Array WORK for Convolution and Correlation Routines

Sample Program: Convolution

References

Work Array `WSAVE` for FFT and VFFT Routines

Work Array `WORK` for Convolution and Correlation Routines