| C H A P T E R 3 |
|
Parallelizing Sun C Code |
The Sun C compiler can optimize code to run on SPARC shared-memory multiprocessor machines. The process is called parallelizing. The compiled code can execute in parallel using the multiple processors on the system. This chapter explains how you can take advantage of the compiler's parallelizing features.
The C compiler generates parallel code for those loops that it determines are safe to parallelize. Typically, these loops have iterations that are independent of each other. For such loops, it does not matter in what order the iterations are executed or if they are executed in parallel. Many, though not all, vector loops fall into this category.
Because of the way aliasing works in C, it is difficult to determine the safety of parallelization. To help the compiler, Sun C offers pragmas and additional pointer qualifications to provide aliasing information known to the programmer that the compiler cannot determine.
The following example illustrates how to enable and control parallelized C:
% cc -fast -xO4 -xautopar example.c -o example |
This generates an executable called example, which can be executed normally. If you wish to take advantage of multiprocessor execution, see Section A.3.65, -xautopar.
You can compile your code so that it complies with the OpenMP specification. For more information on the OpenMP specification for C, visit the web site at http://www.openmp.org/specs/.
To take advantage of the compiler's OpenMP support, you need to issue the compiler's -xopenmp option. See Section A.3.101, -xopenmp[=i].
The OpenMP runtime system can issue warnings for non-fatal errors. Use the following function to register a call back function to handle these warnings:
int sunw_mp_register_warn(void (*func) (void *) )
You can access the prototype for this function by issuing a #include preprocessor directive for <sunw_mp_misc.h>.
If you do not want to register a function, set the environment variable SUNW_MP_WARN to TRUE and the warning messages are sent to stderr. For more information on SUNW_MP_WARN, see SUNW_MP_WARN.
For information specific to this implementation of OpenMP, see Appendix G.
There are four environment variables that relate to parallelized C:
Set the PARALLEL environment variable if you can take advantage of multiprocessor execution. The PARALLEL environment variable specifies the number of processors available to the program. The following example shows that PARALLEL is set to two:
% setenv PARALLEL 2 |
If the target machine has multiple processors, the threads can map to independent processors. Running the program leads to the creation of two threads that execute the parallelized portions of the program.
Currently, the starting thread of a program creates bound threads. Once created, these bound threads participate in executing the parallel part of a program (parallel loop, parallel region, etc.) and keep spin-waiting while the sequential part of the program runs. These bound threads never sleep or stop until the program terminates. Having these threads spin-wait generally gives the best performance when a parallelized program runs on a dedicated system. However, threads that are spin-waiting use system resources.
Use the SUNW_MP_THR_IDLE environment variable to control the status of each thread after it finishes its share of a parallel job.
% setenv SUNW_MP_THR_IDLE value |
You can substitute either spin or sleep[n s|n ms] for value. The default is spin, which means the thread should spin (or busy-wait) after completing a parallel task, until a new parallel task arrives.
The other choice, sleep[n s|n ms] puts the thread to sleep after spin-waiting n units. The wait unit can be seconds (s, the default unit) or milliseconds (ms), where 1s means one second, and 10ms means ten milliseconds. sleep with no arguments puts the thread to sleep immediately after completing a parallel task. sleep, sleep0, sleep0s, and sleep0ms are all equivalent.
If a new job arrives before n units is reached, the thread stops spin-waiting and starts doing the new job. If SUNW_MP_THR_IDLE contains an illegal value or isn't set, spin is used as the default.
Set this environment variable to TRUE to print warning messages from OpenMP and other parallelization runtime-systems.
% setenv SUNW_MP_WARN TRUE |
If you registered a function by using sunw_mp_register_warn() to handle warning messages, then SUNW_MP_WARN prints no warning messages, even if you set it to TRUE. If you did not register a function and set SUNW_MP_WARN to TRUE, SUNW_MP_WARN prints the warning messages to stderr. If you do not register a function and you do not set SUNW_MP_WARN, no warning messages are issued. For more information on sunw_mp_register_warn() see Section 3.2.1, Handling OpenMP Runtime Warnings.
The executing program maintains a main memory stack for the master thread and distinct stacks for each slave thread. Stacks are temporary memory address spaces used to hold arguments and automatic variables over subprogram invocations.
The default size of the main stack is about eight megabytes. Use the limit command to display the current main stack size as well as set it.
Each slave thread of a multithreaded program has its own thread stack. This stack mimics the main stack of the master thread but is unique to the thread. The thread's private arrays and variables (local to the thread) are allocated on the thread stack. All slave threads have the same stack size, which is one megabyte for 32-bit applications and two megabytes for 64-bit applications by default. The size is set with the STACKSIZE environment variable:
% setenv STACKSIZE 8192 <- Set thread stack size to 8 Mb |
Setting the thread stack size to a value larger than the default may be necessary for most parallelized code.
Sometimes the compiler may generate a warning message that indicates a bigger stack size is needed. However, it may not be possible to know just how large to set it, except by trial and error, especially if private/local arrays are involved. If the stack size is too small for a thread to run, the program will abort with a segmentation fault.
The keyword restrict can be used with parallelized C. The proper use of the keyword restrict helps the optimizer in understanding the aliasing of data required to determine if a code sequence can be parallelized. Refer to See C99 Keywords for details.
The C compiler performs analysis on loops in programs to determine if it is safe to execute different iterations of the loops in parallel. The purpose of this analysis is to determine if any two iterations of the loop could interfere with each other. Typically this happens if one iteration of a variable could read a variable while another iteration is writing the very same variable. Consider the following program fragment:
for (i=1; i < 1000; i++) { sum = sum + a[i]; /* S1 */ } |
In CODE EXAMPLE 3-1 any two successive iterations, i and i+1, will write and read the same variable sum. Therefore, in order for these two iterations to execute in parallel some form of locking on the variable would be required. Otherwise it is not safe to allow the two iterations to execute in parallel.
However, the use of locks imposes overhead that might slowdown the program. The C compiler will not ordinarily parallelize the loop in CODE EXAMPLE 3-1. In CODE EXAMPLE 3-1 there is a data dependence between two iterations of the loop. Consider another example:
for (i=1; i < 1000; i++) { a[i] = 2 * a[i]; /* S1 */ } |
In this case each iteration of the loop references a different array element. Therefore different iterations of the loop can be executed in any order. They may be executed in parallel without any locks because no two data elements of different iterations can possibly interfere.
The analysis performed by the compiler to determine if two different iterations of a loop could reference the same variable is called data dependence analysis. Data dependences prevent loop parallelization if one of the references writes to the variable. The dependence analysis performed by the compiler can have three outcomes:
In CODE EXAMPLE 3-3, whether or not two iterations of the loop write to the same element of array a depends on whether or not array b contains duplicate elements. Unless the compiler can determine this fact, it assumes there is a dependence and does not parallelize the loop.
for (i=1; i < 1000; i++) { a[b[i]] = 2 * a[i]; } |
The parallel execution of loops is performed by Solaris threads. The thread starting the initial execution of the program is called the master thread. At program start-up the master thread creates multiple slave threads as shown in the following figure. At the end of the program all the slave threads are terminated. Slave thread creation is performed exactly once to minimize the overhead.
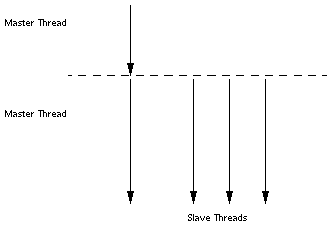
After start-up, the master thread starts the execution of the program while slave threads wait idly. When the master thread encounters a parallel loop, different iterations of the loop are distributed among the slave and master threads which start the execution of the loop. After each thread finishes execution of its chunk it synchronizes with the remaining threads. This synchronization point is called a barrier. The master thread cannot continue executing the remainder of the program until all the threads have finished their work and reached the barrier. The slave threads go into a wait state after the barrier waiting for more parallel work, and the master thread continues to execute the program.
During this process, various overheads can occur:
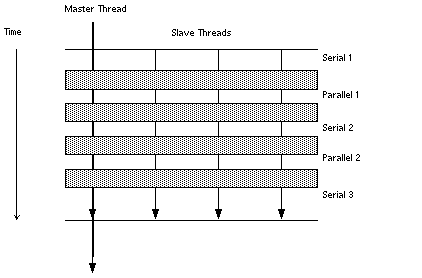
In general, there may be some parallel loops for which the amount of useful work performed is not enough to justify the overhead. For such loops, there may be appreciable slowdown. In the following figure, a loop is parallelized. However the barriers, represented by horizontal bars, introduce significant overhead. The work between the barriers is performed serially or in parallel as indicated. The amount of time required to execute the loop in parallel is considerably less than the amount of time required to synchronize the master and slave threads at the barriers.
There are some data dependences for which the compiler may still be able to parallelize a loop. Consider the following example.
for (i=1; i < 1000; i++) { t = 2 * a[i]; /* S1 */ b[i] = t; /* S2 */ } |
In this example, assuming that arrays a and b are non-overlapping arrays, there appears to be a data dependence in any two iterations due to the variable t. The following statements execute during iterations one and two.
t = 2*a[1]; /* 1 */ b[1] = t; /* 2 */ t = 2*a[2]; /* 3 */ b[2] = t; /* 4 */ |
Because statements one and three modify the variable t, the compiler cannot execute them in parallel. However, the value of t is always computed and used in the same iteration so the compiler can use a separate copy of t for each iteration. This eliminates the interference between different iterations due to such variables. In effect, we have made variable t as a private variable for each thread executing that iteration. This can be illustrated as follows:
for (i=1; i < 1000; i++) { pt[i] = 2 * a[i]; /* S1 */ b[i] = pt[i]; /* S2 */ } |
CODE EXAMPLE 3-6 is essentially the same example as CODE EXAMPLE 3-3, but each scalar variable reference t is now replaced by an array reference pt. Each iteration now uses a different element of pt, and this results in eliminating any data dependencies between any two iterations. Of course one problem with this illustration is that it may lead to an extra large array. In practice, the compiler only allocates one copy of the variable for each thread that participates in the execution of the loop. Each such variable is, in effect, private to the thread.
The compiler can also privatize array variables to create opportunities for parallel execution of loops. Consider the following example:
for (i=1; i < 1000; i++) { for (j=1; j < 1000; j++) { x[j] = 2 * a[i]; /* S1 */ b[i][j] = x[j]; /* S2 */ } } |
In CODE EXAMPLE 3-7, different iterations of the outer loop modify the same elements of array x, and thus the outer loop cannot be parallelized. However, if each thread executing the outer loop iterations has a private copy of the entire array x, then there would be no interference between any two iterations of the outer loop. This is illustrated as follows:
for (i=1; i < 1000; i++) { for (j=1; j < 1000; j++) { px[i][j] = 2 * a[i]; /* S1 */ b[i][j] = px[i][j]; /* S2 */ } } |
As in the case of private scalars, it is not necessary to expand the array for all the iterations, but only up to the number of threads executing in the systems. This is done automatically by the compiler by allocating one copy of the original array in the private space of each thread.
Privatization of variables can be very useful for improving the parallelism in the program. However, if the private variable is referenced outside the loop then the compiler needs to assure that it has the right value. Consider the following example:
for (i=1; i < 1000; i++) { t = 2 * a[i]; /* S1 */ b[i] = t; /* S2 */ } x = t; /* S3 */ |
In CODE EXAMPLE 3-9 the value of t referenced in statement S3 is the final value of t computed by the loop. After the variable t has been privatized and the loop has finished executing, the right value of t needs to be stored back into the original variable. This is called storeback. This is done by copying the value of t on the final iteration back to the original location of variable t. In many cases the compiler can do this automatically. But there are situations where the last value cannot be computed so easily:
for (i=1; i < 1000; i++) { if (c[i] > x[i] ) { /* C1 */ t = 2 * a[i]; /* S1 */ b[i] = t; /* S2 */ } } x = t*t; /* S3 */ |
For correct execution, the value of t in statement S3 is not, in general, the value of t on the final iteration of the loop. It is in fact the last iteration for which the condition C1 is true. Computing the final value of t is quite hard in the general cases. In cases like this the compiler will not parallelize the loop.
There are cases when there is a real dependence between iterations of a loop and the variables causing the dependence cannot simply be privatized. This can arise, for example, when values are being accumulated from one iteration to the next.
for (i=1; i < 1000; i++) { sum += a[i]*b[i]; /* S1 */ } |
In CODE EXAMPLE 3-11, the loop computes the vector product of two arrays into a common variable called sum. This loop cannot be parallelized in a simple manner. The compiler can take advantage of the associative nature of the computation in statement S1 and allocate a private variable called psum[i] for each thread. Each copy of the variable psum[i] is initialized to 0. Each thread computes its own partial sum in its own copy of the variable psum[i]. Before crossing the barrier, all the partial sums are added onto the original variable sum. In this example, the variable sum is called a reduction variable because it computes a sum-reduction. However, one danger of promoting scalar variables to reduction variables is that the manner in which rounded values are accumulated can change the final value of sum. The compiler performs this transformation only if you specifically give permission for it to do so.
If the compiler does not parallelized a portion of a program where a significant amount of time is spent, then no speedup occurs. This is basically a consequence of Amdahls Law. For example, if a loop that accounts for five percent of the execution time of a program is parallelized, then the overall speedup is limited to five percent. However, there may not be any improvement depending on the size of the workload and parallel execution overheads.
As a general rule, the larger the fraction of program execution that is parallelized, the greater the likelihood of a speedup.
Each parallel loop incurs a small overhead during start-up and shutdown. The start overhead includes the cost of work distribution, and the shutdown overhead includes the cost of the barrier synchronization. If the total amount of work performed by the loop is not big enough then no speedup will occur. In fact the loop might even slow down. So if a large amount of program execution is accounted by a large number of short parallel loops, then the whole program may slow down instead of speeding up.
The compiler performs several loop transformations that try to increase the granularity of the loops. Some of these transformations are loop interchange and loop fusion. So in general, if the amount of parallelism in a program is small or is fragmented among small parallel regions, then the speedup is less.
Often scaling up a problem size improves the fraction of parallelism in a program. For example, consider a problem that consists of two parts: a quadratic part that is sequential, and a cubic part that is parallelizable. For this problem the parallel part of the workload grows faster than the sequential part. So at some point the problem will speedup nicely, unless it runs into resource limitations.
It is beneficial to try some tuning, experimentation with directives, problem sizes and program restructuring in order to achieve benefits from parallel C.
Fixed problem-size speedup is generally governed by Amdahl's law. Amdahl's Law simply says that the amount of parallel speedup in a given problem is limited by the sequential portion of the problem.The following equation describes the speedup of a problem where F is the fraction of time spent in sequential region, and the remaining fraction of the time is spent uniformly among P processors. If the second term of the equation drops to zero, the total speedup is bounded by the first term, which remains fixed.
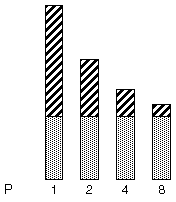
The following figure illustrates this concept diagrammatically. The darkly shaded portion represents the sequential part of the program, and remains constant for one, two, four, and eight processors, while the lightly shaded portion represents the parallel portion of the program that can be divided uniformly among an arbitrary number of processors.
 [ D ]
[ D ]
In reality, however, you may incur overheads due to communication and distribution of work to multiple processors. These overheads may or may not be fixed for arbitrary number of processors used.
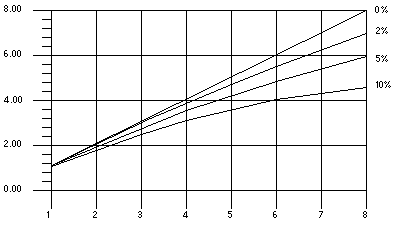
FIGURE 3-4 illustrates the ideal speedups for a program containing 0%, 2%, 5%, and 10% sequential portions. Here, no overhead is assumed.
 [ D ]
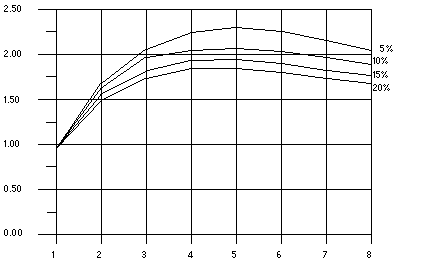
[ D ]Once the overheads are incorporated in the model the speedup curves change dramatically. Just for the purposes of illustration we assume that overheads consist of two parts: a fixed part which is independent of the number of processors, and a non-fixed part that grows quadratically with the number of the processors used:
In this equation, K1 and K2 are some fixed factors. Under these assumptions the speedup curve is shown in the following figure. It is interesting to note that in this case the speedups peak out. After a certain point adding more processors is detrimental to performance as shown in the following figure.
 [ D ]
[ D ]Amdahls Law can be misleading for predicting parallel speedups in real problems. The fraction of time spent in sequential sections of the program sometimes depends on the problem size. That is, by scaling the problem size, you may improve the chances of speedup. The following example demonstrates this.
Assume an ideal overhead of zero and assume that only the second loop nest is executed in parallel. It is easy to see that for small problem sizes (i.e. small values of n), the sequential and parallel parts of the program are not so far from each other. However, as n grows larger, the time spent in the parallel part of the program grows faster than the time spent in the sequential part. For this problem, it is beneficial to increase the number of processors as the problem size increases.
Loop scheduling is the process of distributing iterations of a parallel loop to multiple threads. In order to maximize the speedup, it is important that the work be distributed evenly among the threads while not imposing too much overhead. The compiler offers several types of scheduling for different situations.
It is beneficial to divide the work evenly among the different threads on the system when the work performed by different iterations of a loop is the same. This approach is known as static scheduling.
for (i=1; i < 1000; i++) { sum += a[i]*b[i]; /* S1 */ } |
Under static or chunk scheduling, each thread will get the same number of iterations. If there were 4 threads, then in the above example, each thread will get 250 iterations. Provided there are no interruptions and each thread progresses at the same rate, all the threads will complete at the same time.
Static scheduling will not achieve good load balance, in general, when the work performed by each iteration varies. In static scheduling, each thread grabs the same chunk of iterations. Each thread, except the master thread, upon completion of its chunk waits to participate in the next parallel loop execution. The master thread continues execution of the program. In self scheduling, each thread grabs a different small chunk of iteration and after completion of its assigned chunk, tries to acquire more chunks from the same loop.
In guided self scheduling (GSS), each thread gets successively smaller number of chunks. In cases where the size of each iteration varies, GSS can help balance the load.
The compiler performs several loop restructuring transformations to help improve the parallelization of a loop in programs. Some of these transformations can also improve the single processor execution of loops as well. The transformations performed by the compiler are described below.
Often loops contain a few statements that cannot be executed in parallel and many statements that can be executed in parallel. Loop Distribution attempts to remove the sequential statements into a separate loop and gather the parallelizable statements into a different loop. This is illustrated in the following example:
for (i=0; i < n; i++) { x[i] = y[i] + z[i]*w[i]; /* S1 */ a[i+1] = (a[i-1] + a[i] + a[i+1]/3.0; /* S2 */ y[i] = z[i] - x[i]; /* S3 */ } |
Assuming that arrays x, y, w, a, and z do not overlap, statements S1 and S3 can be parallelized but statement S2 cannot be. Here is how the loop looks after it is split or distributed into two different loops:
After this transformation, loop L1 does not contain any statements that prevent the parallelization of the loop and may be executed in parallel. Loop L2, however, still has a non-parallelizable statement from the original loop.
Loop distribution is not always profitable or safe to perform. The compiler performs analysis to determine the safety and profitability of distribution.
If the granularity of a loop, or the work performed by a loop, is small, the performance gain from distribution may be insignificant. This is because the overhead of parallel loop start-up is too high compared to the loop workload. In such situations, the compiler uses loop fusion to combine several loops into a single parallel loop, and thus increase the granularity of the loop. Loop fusion is easy and safe when loops with identical trip counts are adjacent to each other. Consider the following example:
The two short parallel loops are next to each other, and can be safely combined as follows:
/* L3: a larger parallel loop */ for (i=0; i < 100; i++) { a[i] = a[i] + b[i]; /* S1 */ b[i] = a[i] * d[i]; /* S2 */ } |
The new loop generates half the parallel loop execution overhead. Loop fusion can also help in other ways. For example if the same data is referenced in two loops, then combining them can improve the locality of reference.
However, loop fusion is not always safe to perform. If loop fusion creates a data dependence that did not exist before then the fusion may result in incorrect execution. Consider the following example:
If the loops in CODE EXAMPLE 3-18 are fused, a data dependence is created from statement S2 to S1. In effect, the value of a[i] in the right hand side of statement S1 is computed in statement S2. If the loops are not fused, this would not happen. The compiler performs safety and profitability analysis to determine if loop fusion should be done. Often, the compiler can fuse an arbitrary number of loops. Increasing the granularity in this manner can sometimes push a loop far enough up for it to be profitable for parallelization.
It is generally more profitable to parallelize the outermost loop in a nest of loops, since the overheads incurred are small. However, it is not always safe to parallelize the outermost loops due to dependences that might be carried by such loops. This is illustrated in the following:
for (i=0; i <n; i++) { for (j=0; j <n; j++) { a[j][i+1] = 2.0*a[j][i-1]; } } |
In this example, the loop with the index variable i cannot be parallelized, because of a dependency between two successive iterations of the loop. The two loops can be interchanged and the parallel loop (the j-loop) becomes the outer loop:
for (j=0; j<n; j++) { for (i=0; i<n; i++) { a[j][i+1] = 2.0*a[j][i-1]; } } |
The resulting loop incurs an overhead of parallel work distribution only once, while previously, the overhead was incurred n times. The compiler performs safety and profitability analysis to determine whether to perform loop interchange.
ISO C aliasing can often prevent loops from getting parallelized. Aliasing occurs when there are two possible references to the same memory location. Consider the following example:
void copy(float a[], float b[], int n) { int i; for (i=0; i < n; i++) { a[i] = b[i]; /* S1 */ } } |
Since variables a and b are parameters, it is possible that a and b may be pointing to overlapping regions of memory; e.g, if copy were called as follows:
copy (x[10], x[11], 20); |
In the called routine, two successive iterations of the copy loop may be reading and writing the same element of the array x. However, if the routine copy were called as follows then there is no possibility of overlap in any of the 20 iterations of the loop:
copy (x[10], x[40], 20); |
In general, it is not possible for the compiler to analyze this situation correctly without knowing how the routine is called. The compiler provides a keyword extension to ISO C that lets you convey this kind of aliasing information. See Section 3.8.2, Restricted Pointers for more information.
Part of the aliasing problem is that the C language can define array referencing and definition through pointer arithmetic. In order for the compiler to effectively parallelize loops, either automatically or explicitly with pragmas, all data that is laid out as an array must be referenced using C array reference syntax and not pointers. If pointer syntax is used, the compiler cannot determine the relationship of the data between different iterations of a loop. Thus it will be conservative and not parallelize the loop.
In order for a compiler to effectively perform parallel execution of a loop, it needs to determine if certain lvalues designate distinct regions of storage. Aliases are lvalues whose regions of storage are not distinct. Determining if two pointers to objects are aliases is a difficult and time consuming process because it could require analysis of the entire program. Consider function vsq() below:
void vsq(int n, double * a, double * b) { int i; for (i=0; i<n; i++) { b[i] = a[i] * a[i]; } } |
The compiler can parallelize the execution of the different iterations of the loops if it knows that pointers a and b access different objects. If there is an overlap in objects accessed through pointers a and b then it would be unsafe for the compiler to execute the loops in parallel. At compile time, the compiler does not know if the objects accessed by a and b overlap by simply analyzing the function vsq(); the compiler may need to analyze the whole program to get this information.
Restricted pointers are used to specify pointers which designate distinct objects so that the compiler can perform pointer alias analysis. The following is an example of function vsq() in which function parameters are declared as restricted pointers:
void vsq(int n, double * restrict a, double * restrict b) |
Pointers a and b are declared as restricted pointers, so the compiler knows that a and b point to distinct regions of storage. With this alias information, the compiler is able to parallelize the loop.
The keyword restrict is a type-qualifier, like volatile, and it shall only qualify pointer types. restrict is recognized as a keyword when you use -xc99=%all (except with -Xs). There are situations in which you may not want to change the source code. You can specify that pointer-valued function-parameters be treated as restricted pointers by using the following command line option:
-xrestrict=[func1,...,funcn] |
If a function list is specified, then pointer parameters in the specified functions are treated as restricted; otherwise, all pointer parameters in the entire C file are treated as restricted. For example, -xrestrict=vsq, qualifies the pointers a and b given in the first example of the function vsq() with the keyword restrict.
It is critical that you use restrict correctly. If pointers qualified as restricted pointers point to objects which are not distinct, the compiler can incorrectly parallelize loops resulting in undefined behavior. For example, assume that pointers a and b of function vsq() point to objects which overlap, such that b[i] and a[i+1] are the same object. If a and b are not declared as restricted pointers the loops will be executed serially. If a and b are incorrectly qualified as restricted pointers the compiler may parallelize the execution of the loops, which is not safe, because b[i+1] should only be computed after b[i] is computed.
Often, there is not enough information available for the compiler to make a decision on the legality or profitability of parallelization. Sun ISO C supports pragmas that allow the programmer to effectively parallelize loops that otherwise would be too difficult or impossible for the compiler to handle.
There are two serial pragmas, and both apply to for loops:
The #pragma MP serial_loop pragma indicates to the compiler that the next for loop is not to be automatically parallelized.
The #pragma MP serial_loop_nested pragma indicates to the compiler that the next for loop and any for loops nested within the scope of this for loop are not to be automatically parallelized. The scope of the serial_loop_nested pragma does not extend beyond the scope of the loop to which it applies.
There is one parallel pragma: #pragma MP taskloop [options].
The MP taskloop pragma can, optionally, take one or more of the following arguments.
Only one option can be specified per MP taskloop pragma; however, the pragmas are cumulative and apply to the next for loop encountered within the current block in the source code:
#pragma MP taskloop maxcpus(4) #pragma MP taskloop shared(a,b) #pragma MP taskloop storeback(x) |
These options may appear multiple times prior to the for loop to which they apply. In case of conflicting options, the compiler will issue a warning message.
An MP taskloop pragma applies to the next for loop within the current block. There is no nesting of parallelized for loops by parallelized C.
An MP taskloop pragma suggests to the compiler that, unless otherwise disallowed, the specified for loop should be parallelized.
Any for loop with irregular control flow and unknown loop iteration increment is ineligible for parallelization. For example, for loops containing setjmp, longjmp, exit, abort, return, goto, labels, and break should not be considered as candidates for parallelization.
Of particular importance is to note that for loops with inter-iteration dependencies can be eligible for explicit parallelization. This means that if an MP taskloop pragma is specified for such a loop the compiler will simply honor it, unless the for loop is disqualified. It is the user's responsibility to make sure that such explicit parallelization will not lead to incorrect results.
If both the serial_loop or serial_loop_nested and taskloop pragmas are specified for a for loop, the last one specified will prevail.
Consider the following example:
#pragma MP serial_loop_nested for (i=0; i<100; i++) { # pragma MP taskloop for (j=0; j<1000; j++) { ... } } |
The i loop will not be parallelized but the j loop might be.
#pragma MP taskloop maxcpus (number_of_processors) specifies the number of processors to be used for this loop, if possible.
The value of maxcpus must be a positive integer. If maxcpus equals 1, then the specified loop will be executed in serial. (Note that setting maxcpus to be 1 is equivalent to specifying the serial_loop pragma.) The smaller of the values of maxcpus or the interpreted value of the PARALLEL environment variable will be used. When the environment variable PARALLEL is not specified, it is interpreted as having the value 1.
If more than one maxcpus pragma is specified for a for loop, the last one specified will prevail.
A variable used in a loop is classified as being either a private, shared, reduction, or readonly variable. The variable belongs to only one of these classifications. A variable can only be classified as a reduction or readonly variable through an explicit pragma. See #pragma MP taskloop reduction and #pragma MP taskloop readonly. A variable can be classified as being either a private or shared variable through an explicit pragma or through the following default scoping rules.
A private variable is one whose value is private to each processor processing some iterations of a for loop. In other words, the value assigned to a private variable in one iteration of a for loop is not propagated to other processors processing other iterations of that for loop. A shared variable, on the other hand, is a variable whose current value is accessible by all processors processing iterations of a for loop. The value assigned to a shared variable by one processor working on iterations of a loop may be seen by other processors working on other iterations of the loop. Loops being explicitly parallelized through use of #pragma MP taskloop directives, that contain references to shared variables, must ensure that such sharing of values does not cause any correctness problems (such as race conditions). No synchronization is provided by the compiler on updates and accesses to shared variables in an explicitly parallelized loop.
In analyzing explicitly parallelized loops, the compiler uses the following "default scoping rules" to determine whether a variable is private or shared:
It is highly recommended that all variables used in an explicitly parallelized for loop be explicitly classified as one of shared, private, reduction, or readonly, to avoid the "default scoping rules."
Since the compiler does not perform any synchronization on accesses to shared variables, extreme care must be exercised before using an MP taskloop pragma for a loop that contains, for example, array references. If inter-iteration data dependencies exist in such an explicitly parallelized loop, then its parallel execution may give erroneous results. The compiler may or may not be able to detect such a potential problem situation and issue a warning message. In any case, the compiler will not disable the explicit parallelization of loops with potential shared variable problems.
#pragma MP taskloop private (list_of_private_variables)
Use this pragma to specify all the variables that should be treated as private variables for this loop. All other variables used in the loop that are not explicitly specified as shared, readonly, or reduction variables, are either shared or private as defined by the default scoping rules.
A private variable is one whose value is private to each processor processing some iterations of a loop. In other words, the value assigned to a private variable by one of the processors working on iterations of a loop is not propagated to other processors processing other iterations of that loop. A private variable has no initial value at the start of each iteration of a loop and must be set to a value within the iteration of a loop prior to its first use within that iteration. Execution of a program with a loop containing an explicitly declared private variable whose value is used prior to being set will result in undefined behavior.
#pragma MP taskloop shared (list_of_shared_variables)
Use this pragma to specify all the variables that should be treated as shared variables for this loop. All other variables used in the loop that are not explicitly specified as private, readonly, storeback or reduction variables, are either shared or private as defined by the default scoping rules.
A shared variable is a variable whose current value is accessible by all processors processing iterations of a for loop. The value assigned to a shared variable by one processor working on iterations of a loop may be seen by other processors working on other iterations of the loop.
#pragma MP taskloop readonly (list_of_readonly_variables)
readonly variables are a special class of shared variables that are not modified in any iteration of a loop. Use this pragma to indicate to the compiler that it may use a separate copy of that variable's value for each processor processing iterations of the loop.
#pragma MP taskloop storeback (list_of_storeback_variables)
Use this pragma to specify all the variables to be treated as storeback variables.
A storeback variable is one whose value is computed in a loop, and this computed value is then used after the termination of the loop. The last loop iteration values of storeback variables are available for use after the termination of the loop. Such a variable is a good candidate to be declared explicitly via this directive as a storeback variable when the variable is a private variable, whether by explicitly declaring the variable private or by the default scoping rules.
Note that the storeback operation for a storeback variable occurs at the last iteration of the explicitly parallelized loop, regardless of whether or not that iteration updates the value of the storeback variable. In other words, the processor that processes the last iteration of a loop may not be the same processor that currently contains the last updated value for a storeback variable. Consider the following example:
#pragma MP taskloop private(x) #pragma MP taskloop storeback(x) for (i=1; i <= n; i++) { if (...) { x=... } } printf ("%d", x); |
In the previous example the value of the storeback variable x printed out via the printf() call may not be the same as that printed out by a serial version of the i loop, because in the explicitly parallelized case, the processor that processes the last iteration of the loop (when i==n), which performs the storeback operation for x may not be the same processor that currently contains the last updated value for x. The compiler will attempt to issue a warning message to alert the user of such potential problems.
In an explicitly parallelized loop, variables referenced as arrays are not treated as storeback variables. Hence it is important to include them in the list_of_storeback_variables if such storeback operation is desired (for example, if the variables referenced as arrays have been declared as private variables).
Use this pragma to specify all the private variables of a loop that you want to be treated as storeback variables. The syntax of this pragma is as follows:
It is often convenient to use this form, rather than list out each private variable of a loop when declaring each variable as storeback variables.
#pragma MP taskloop reduction (list_of_reduction_variables) specifies that all the variables appearing in the reduction list will be treated as reduction variables for the loop. A reduction variable is one whose partial values can be individually computed by each of the processors processing iterations of the loop, and whose final value can be computed from all its partial values. The presence of a list of reduction variables can facilitate the compiler in identifying that the loop is a reduction loop, allowing generation of parallel reduction code for it. Consider the following example:
#pragma MP taskloop reduction(x) for (i=0; i<n; i++) { x = x + a[i]; } |
the variable x is a (sum) reduction variable and the i loop is a(sum) reduction loop.
The Sun ISO C compiler supports several pragmas that can be used in conjunction with the taskloop pragma to control the loop scheduling strategy for a given loop. The syntax for this pragma is:
#pragma MP taskloop schedtype (scheduling_type)
This pragma can be used to specify the specific scheduling_type to be used to schedule the parallelized loop. Scheduling_type can be one of the following:
#pragma MP taskloop maxcpus(4) #pragma MP taskloop schedtype(static) for (i=0; i<1000; i++) { ... } |
#pragma MP taskloop maxcpus(4) #pragma MP taskloop schedtype(self(120)) for (i=0; i<1000; i++) { ... } |
#pragma MP taskloop maxcpus(4) #pragma MP taskloop schedtype(gss(10)) for (i=0; i<1000; i++) { ... } |
Copyright © 2002, Sun Microsystems, Inc. All rights reserved.