CMS Help: Understanding Certificates
Previous Next Contents


Chapter 1 Understanding Certificates

This guide describes how to get a new certificate, renew an existing certificate, and perform other operations with Netscape Certificate Management System. It is intended for users and server administrators who are not familiar with certificates or with Netscape Certificate Management System.

The following sections introduce you to basic concepts that will help you understand certificates and use Certificate Management System. For brief definitions of terms, see the Glossary.


Internet Security Issues
Communication over the Internet uses the Transmission Control Protocol/Internet Protocol (TCP/IP). TCP/IP allows information to be sent from one computer to another through a variety of intermediate computers and separate networks before it reaches its destination.

The great flexibility of TCP/IP has led to its worldwide acceptance as the basic Internet and intranet communications protocol. At the same time, the fact that TCP/IP allows information to pass through intermediate computers makes it possible for a third party to interfere with communications in the following ways:

Normally, users of the many cooperating computers that make up the Internet or other networks don't monitor or interfere with the network traffic that continuously passes through their machines. However, many sensitive personal and business communications over the Internet require precautions that address the threats listed above. Fortunately, some well-established techniques and standards collectively known as public-key cryptography make it relatively easy to take such precautions.

Public-key cryptography and related techniques facilitate the following tasks:

The sections that follow introduce the concepts of public-key cryptography that underlie these capabilities.


Encryption and Decryption
Encryption is the process of scrambling information so it is unintelligible to anyone but the intended recipient. Decryption is the process of unscrambling encrypted information so that it is intelligible again. A cryptographic algorithm, also called a cipher, is set of rules or directions used to encrypt or decrypt data. In most cases, two related algorithms are employed, one for encryption and the other for decryption.

With most modern cryptography, the ability to keep encrypted information secret is based not on the cryptographic algorithm, which is widely known, but on a number called a key that must be used with the algorithm to produce an encrypted result or to decrypt previously encrypted information. Decryption with the correct key is simple. Decryption without the correct key is very difficult, and in some cases impossible for all practical purposes.


Public-Key Cryptography
Public-key cryptography is the name for some well-established techniques and standards that allow an entity to verify its identity electronically or to sign and encrypt electronic data. It involves a pair of keys--a public key and a private key--associated with the entity. The most commonly used implementations of public-key cryptography are based on algorithms patented by RSA Data Security. Therefore, this section describes the RSA approach.

Each public key is published, and the corresponding private key is kept secret. Data encrypted with your public key can be decrypted only with your private key. Figure 1.1 shows a simplified view of the way public-key encryption works.

Figure 1.1    Public-key encryption

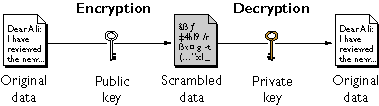
The scheme shown in Figure 1.1 lets you freely distribute a public key, and only you will be able to read data encrypted using this key. In general, to send encrypted data to someone, you encrypt the data with that person's public key, and the person receiving the encrypted data decrypts it with the corresponding private key.

As it happens, the reverse of the scheme shown in Figure 1.1 also works: data encrypted with your private key can be decrypted only with your public key. This would not be a desirable way to encrypt sensitive data, however, because it means that anyone with your public key, which is by definition published, could decrypt the data. Nevertheless, private-key encryption is useful, because it means you can use your private key to sign data with your digital signature--an important requirement for electronic commerce and other commercial applications of cryptography. Client software such as Communicator can then use your public key to confirm that the message was signed with your private key and that it hasn't been tampered with since being signed.


Digital Signatures
Encryption and decryption address the problem of eavesdropping, one of the three Internet security issues mentioned at the beginning of this chapter. But encryption and decryption, by themselves, do not address the other two problems mentioned in Internet Security Issues: tampering and impersonation.

This section describes how public-key cryptography addresses the problem of tampering. The section that follows describes how it addresses the problem of impersonation.

Tamper detection and related authentication techniques rely on a mathematical function called a one-way hash (also called a message digest). A one-way hash is a number of fixed length with the following characteristics:

As mentioned in Public-Key Cryptography, it's possible to use your private key for encryption and your public key for decryption. Although this is not desirable when you are encrypting sensitive information, it is a crucial part of digitally signing any data. Instead of encrypting the data itself, the signing software creates a one-way hash of the data, then uses your private key to encrypt the hash. The encrypted hash, along with other information, such as the name of the hashing algorithm, is known as a digital signature.

Figure 1.2 shows a simplified view of the way a digital signature can be used to validate the integrity of signed data.

Figure 1.2    Using a digital signature to validate data integrity

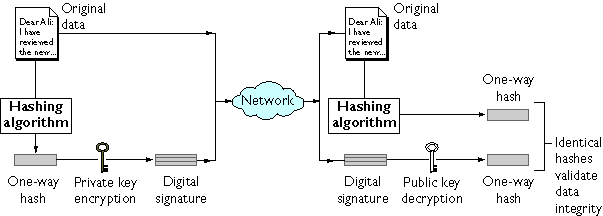
 Figure 1.2 shows two items transferred to the recipient of some signed data: the original data and the digital signature, which is basically a one-way hash (of the original data) that has been encrypted with the signer's private key. To validate the integrity of the data, the receiving software first uses the signer's public key to decrypt the hash. It then uses the same hashing algorithm that generated the original hash to generate a new one-way hash of the same data. (Information about the hashing algorithm used is sent with the digital signature, although this isn't shown in the figure.) Finally, the receiving software compares the new hash against the original hash. If the two hashes match, the data has not changed since it was signed. If they don't match, the data may have been tampered with since it was signed, or the signature may have been created with a private key that doesn't correspond to the public key presented by the signer.

If the two hashes match, the recipient can be certain that the public key used to decrypt the digital signature corresponds to the private key used to create the digital signature. Confirming the identity of the signer, however, also requires some way of confirming that the public key really belongs to a particular person or other entity. Digital identification documents called certificates, which are described in the next section, address this issue.

The significance of a digital signature is comparable to the significance of a handwritten signature. Once you have signed some data, it is difficult to deny doing so later--assuming that the private key has not been compromised or out of the owner's control. This quality of digital signatures provides a high degree of nonrepudiation--that is, digital signatures make it difficult for the signer to deny having signed the data. In some situations, a digital signature may be as legally binding as a handwritten signature.


Certificates
A certificate is an electronic document used to identify an individual, a server, a company, or some other entity and to associate that identity with a public key. Like a driver's license, a credit card, a passport, or other commonly used personal IDs, a certificate provides generally recognized proof of a person's identity. Public-key cryptography uses certificates to address the problem of impersonation (see Internet Security Issues).

To get a driver's license, you typically apply to a government agency, such as the Department of Motor Vehicles, which verifies your identity, your ability to drive, your address, and other information before issuing the license. To get a credit card, you apply to a company that performs a credit check before issuing the ID. To get a library card, you may need to provide only your name and a utility bill with your address on it.

Certificates work much the same way as any of these familiar forms of identification. Certificate authorities (CAs) are entities that validate identities and issue certificates. They can be either independent third parties or organizations running their own certificate-issuing server software (such as Certificate Management System). The methods used to validate an identity vary depending on the policies of a given CA--just as the methods to validate other forms of identification vary depending on who is issuing the ID and the purpose for which it will be used. In general, before issuing a certificate, the CA must use published verification procedures to ensure that an entity requesting a certificate is in fact who it claims to be.

The certificate issued by the CA binds a particular public key to the name of the entity the certificate identifies (such as the name of an employee). Certificates help prevent the use of fake public keys for impersonation. Only the public key certified by the certificate will work with the corresponding private key possessed by the entity identified by the certificate.

In addition to a public key, a certificate always includes the name of the entity it identifies, an expiration date, the name of the CA that issued the certificate, a serial number, and other information. Most importantly, a certificate always includes the digital signature of the issuing CA. The CA's digital signature allows the certificate to function as a "letter of introduction" for users who know and trust the CA but don't know the entity identified by the certificate.


What You Do with Certificate Management System
Certificate Management System allows you to perform the following tasks:

 

Copyright © 2000 Sun Microsystems, Inc. Some preexisting portions Copyright © 2000 Netscape Communications Corp. All rights reserved.