| Skip Navigation Links | |
| Exit Print View | |
|
Application Packaging Developer's Guide Oracle Solaris 10 1/13 Information Library |
| Skip Navigation Links | |
| Exit Print View | |
|
Application Packaging Developer's Guide Oracle Solaris 10 1/13 Information Library |
3. Enhancing the Functionality of a Package (Tasks)
4. Verifying and Transferring a Package
5. Case Studies of Package Creation
6. Advanced Techniques for Creating Packages
The Administrative Defaults File
Becoming Comfortable With Uncertainty
Using Parametric Base Directories
Examples--Using Parametric Base Directories
Example--Analysis Scripts That Walk a BASEDIR
Using Relative Parametric Paths
Example--A request Script That Walks a Relative Parametric Path
Supporting Relocation in a Heterogeneous Environment
Example-A Traditional Relocatable Package
Example-A Traditional Absolute Package
Example-A Traditional Solution
Another Look at Composite Packages
Making Absolute Path Names Look Relocatable
Making Packages Remotely Installable
Example - Installing to a Client System
Example - Installing to a Server or Standalone System
A class archive package, which is an enhancement to the Application Binary Interface (ABI), is one in which certain sets of files have been combined into single files, or archives, and optionally compressed or encrypted. Class archive formats increase initial install speed by up to 30% and improves reliability during installation of packages and patches onto potentially active file systems.
The following sections provide information about the archive package directory structure, keywords, and faspac utility.
The package entry shown in the figure below represents the directory containing the package files. This directory must be the same name as the package.
Figure 6-1 Package Directory Structure
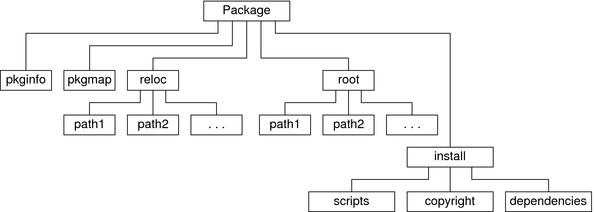
The following lists the functions of the files and directories contained within the package directory.
|
The class archive format allows the package builder to combine files from the reloc and root directories into archives which can be compressed, encrypted, or otherwise processed in any desired way in order to increase install speed, reduce package size, or increase package security.
The ABI allows any file within a package to be assigned to a class. All files within a specific class may be installed to the disk using a custom method defined by a class action script. This custom method may make use of programs available on the target system or programs delivered with the package. The resulting format looks much like the standard ABI format. As shown in the following illustration, another directory is added. Any class of files intended for archive is simply combined into a single file and placed into the archive directory. All archived files are removed from the reloc and root directories and an install class action script is placed into the install directory.
Figure 6-2 Archive Package Directory Structure
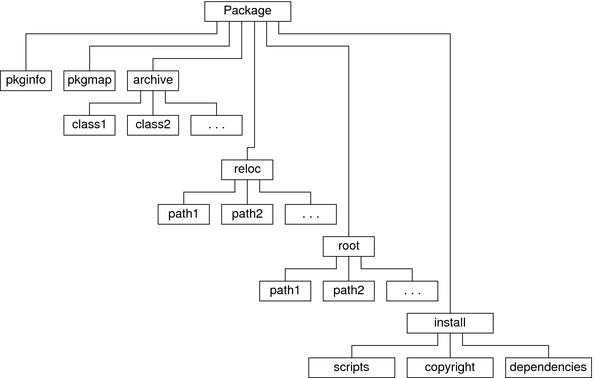
In order to support this new class archive format, three new interfaces in the form of keywords have special meaning within the pkginfo file. These keywords are used to designate classes requiring special treatment. The format of each keyword statement is: keyword=class1[class2 class3 ...]. Each keyword values are defined in the following table.
|
For each archived class a class action script is required. This is a file containing Bourne shell commands which is executed by pkgadd to actually install the files from the archive. If a class action script is found in the install directory of the package, pkgadd turns all responsibility for installation over to that script. The class action script is run with root permissions and can place its files just about anywhere on the target system.
Note - The only keyword that is absolutely necessary in order to implement a class archive package is PKG_SRC_NOVERIFY. The others may be used to increase installation speed or conserve code.
The faspac utility converts a standard ABI package into a class archive format used for bundled packages. This utility archives using cpio and compresses using compress. The resulting package has an additional directory in the top directory called archive. In this directory will be all of the archives named by class. The install directory will contain the class action scripts necessary to unpack each archive. Absolute paths are not archived.
The faspac utility has the following format:
faspac [-m Archive Method] -a -s -q [-d Base Directory] / [-x Exclude List] [List of Packages]
Each faspac command option is described in the following table.
|