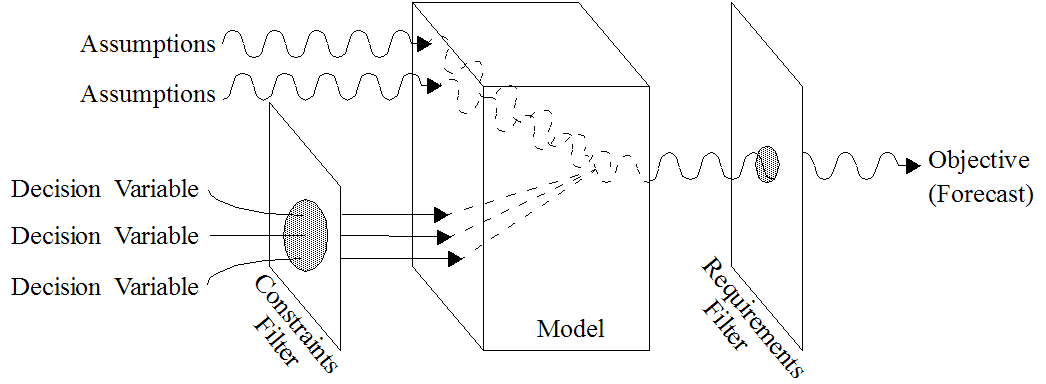
In many cases, however, a deterministic optimization model can’t capture all the relevant intricacies of a practical decision environment. When model data are uncertain and can only be described probabilistically, the objective will have some probability distribution for any chosen set of decision variables. You can find this probability distribution by simulating the model using Crystal Ball. This type of model is called stochastic.
A stochastic optimization model has several additional elements:
Assumptions — Capture the uncertainty of model data using probability distributions.
Forecasts — Are frequency distributions of possible results for the model.
Forecast statistics — Are summary values of a forecast distribution, such as the mean, standard deviation, or variance. You control the optimization by maximizing or minimizing forecast statistics, or setting them to a target.
Requirements — Are additional restrictions on forecast statistics. You can set upper and lower limits for any statistic of a forecast distribution.
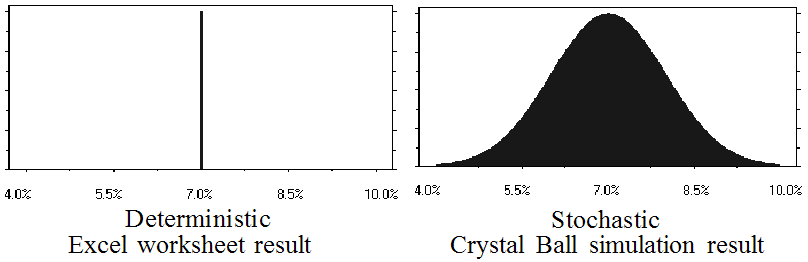
Stochastic models are much more difficult to optimize because they require simulation to compute the objective. While Crystal Ball is designed to solve stochastic models using Crystal Ball, it is also capable of solving deterministic models. Figure 67, Comparison of deterministic and stochastic results shows that deterministic results are a single value, while stochastic results are distributed over a curve.