Except where indicated, this example uses the recommended Crystal Ball run preferences. See Setting Crystal Ball Run Preferences. |
 Perform these steps:
Perform these steps:
With Portfolio Revisited EF.xls open in Crystal Ball, set the number of trials per simulation to 2000 in the Run Preferences dialog.
Start OptQuest from the Crystal Ball Run menu.
As you click Next to step through the problem, note that the objective, decision variables, and constraints are the same as for the original example (Tutorial 2 — Portfolio Allocation Model ).
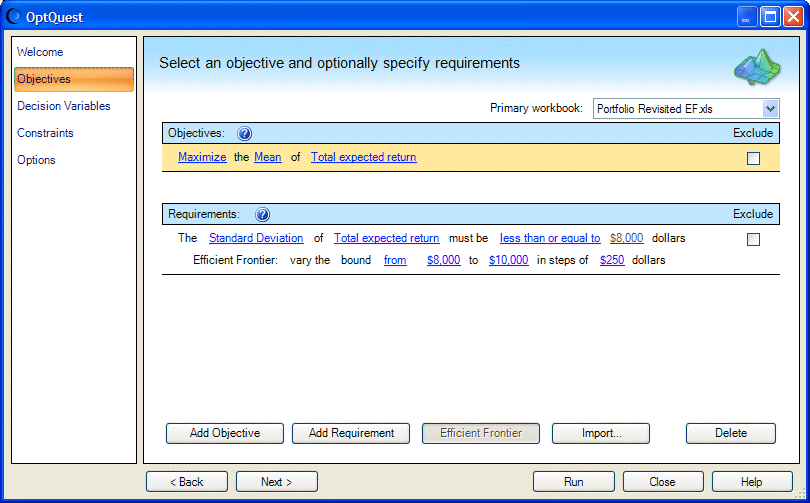
Figure 48, Objectives panel with a variable requirement shows the Objectives panel with the variable requirement needed for efficient frontier testing.
The requirement has a variable upper bound for the standard deviation statistic (less than or equal to $8,000)..
The variable requirement bounds are $8,000 for the lower bound and $10,000 for the upper bound in steps of $250..
Run the optimization for 2000 simulations (set in the Options panel of the OptQuest wizard)..
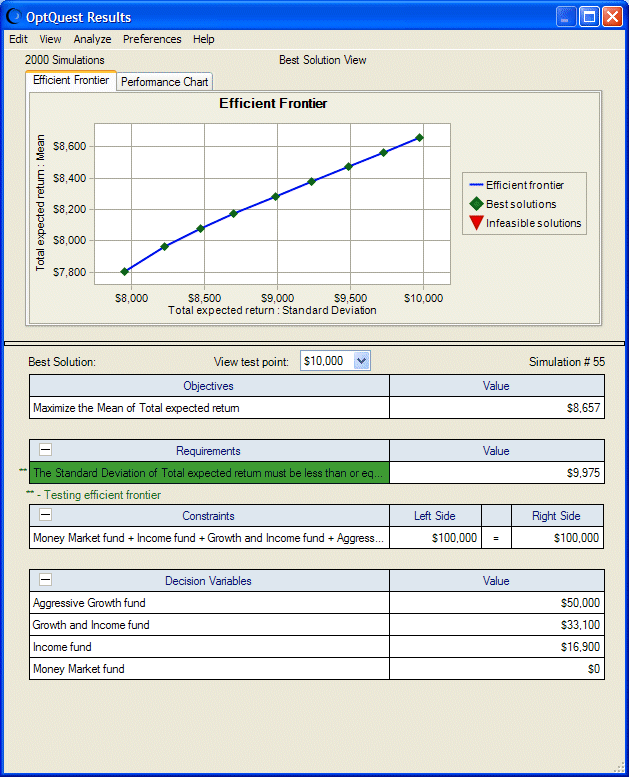
The results are shown in Figure 49, Portfolio Revisited Efficient Frontier optimization results. The mean of total expected return is maximized at $8,657 with fund allocations as follows: Aggressive Growth fund = $50,000; Growth and Income fund = $33,100; Income fund = $16,900; and Money Market fund = $0.
When should you use the Efficient Frontier function? This method is useful when it is difficult to determine reasonable lower or upper bounds for requirement statistics.