L'esempio di analisi dello strumento Simulazione 2D utilizza il modello di Crystal Ball denominato Toxic Waste Site.xlsx (Figura 9.15, «Modello di foglio di calcolo Discarica rifiuti tossici»). Questo modello prevede il rischio di contrarre il cancro da parte della popolazione a causa di una discarica di rifiuti tossici. Il foglio di calcolo contiene due ipotesi di variabilità e due ipotesi di incertezza.
Per generare i risultati, le preferenze di esecuzione di Crystal Ball vengono innanzitutto impostate per l'utilizzo della simulazione Monte Carlo con la stessa sequenza di numeri casuali e un valore iniziale pari a 999. Lo strumento Simulazione 2D viene quindi eseguito con Accertamento rischio come previsione target, Peso corporeo e Volume acqua giornaliero inclusi nell'elenco Variabilità nel riquadro Tipi di ipotesi e le seguenti impostazioni di Opzioni:
Lo strumento Simulazione 2D esegue innanzitutto una prova in un singolo passo per generare un nuovo set di valori per le ipotesi di incertezza. Congela quindi queste ipotesi ed esegue una simulazione per le ipotesi di variabilità nel loop interno.
Lo strumento recupera le informazioni sulle previsioni di Crystal Ball dopo l'esecuzione di ogni loop. Reimposta quindi la simulazione e ripete il processo finché l'esecuzione del loop esterno non viene completata per il numero specificato di simulazioni.
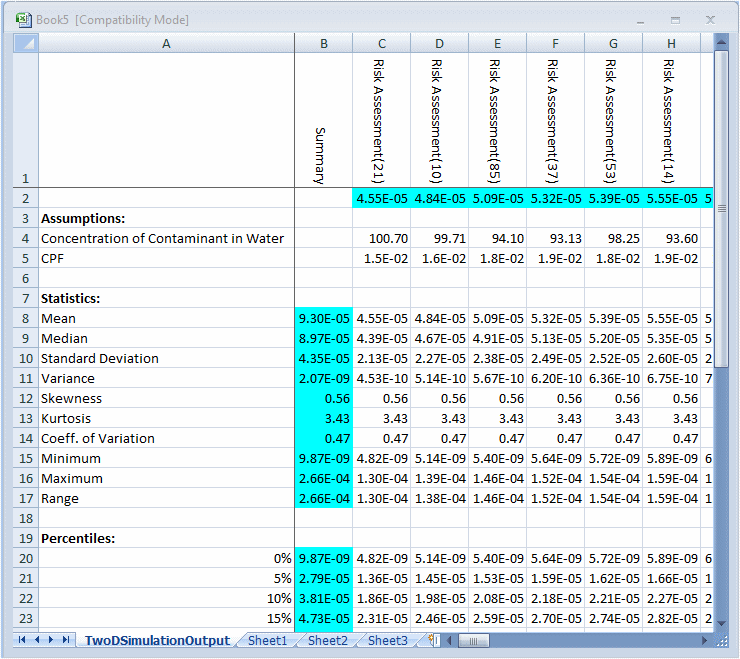
I risultati delle simulazioni vengono visualizzati in una tabella contenente le medie di previsione, i valori delle ipotesi di incertezza e le statistiche (inclusi i percentili) della distribuzione di previsione per ogni simulazione (Figura 9.18, «Tabella dei risultati dello strumento Simulazione 2D»).
Lo strumento rappresenta inoltre graficamente i risultati delle simulazioni bidimensionali in un grafico overlay e in un grafico di tendenza.
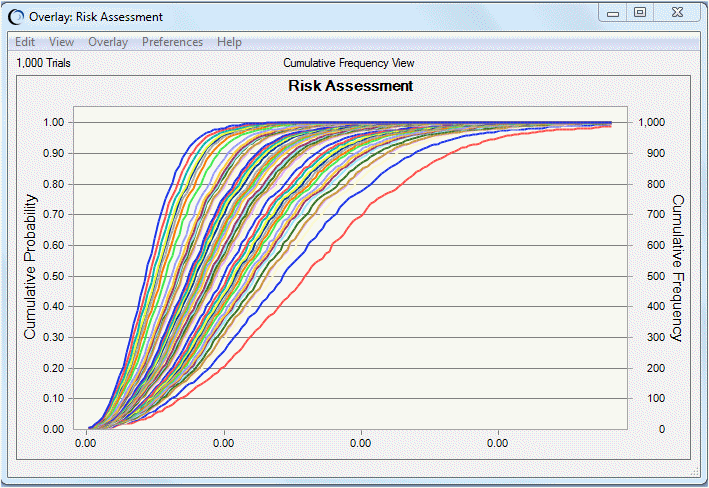
È possibile impostare le preferenze del grafico overlay in modo da mostrare le curve di rischio per le simulazioni per diversi set di valori di ipotesi di incertezza. A tale scopo, impostare l'opzione Tipo di grafico per ogni serie su A linee e selezionare la vista Frequenza cumulativa. Per comodità, utilizzare i tasti di scelta rapida per i grafici, ovvero CTRL+T per il tipo di grafico e CTRL+D per la vista. Facoltativamente, utilizzare CTRL+N per spostare o rimuovere la legenda e CTRL+M per spostarsi in sequenza tra le linee indicatore di tendenza centrali.
Per questo esempio, la Figura 9.19, «Grafico overlay delle curve di rischio» mostra che le curve di rischio sono per lo più raggruppate densamente verso il centro, mentre poche curve più esterne sono disseminate verso l'asse Frequenza cumulativa, indicando la scarsa probabilità di un rischio molto più elevato.
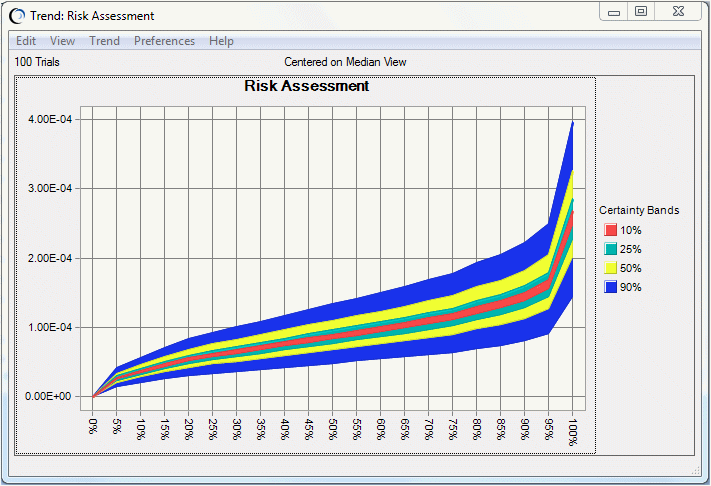
Il grafico di tendenza (Figura 9.20, «Suddivisioni certezza del grafico di tendenza») mostra le suddivisioni della certezza per i percentili delle curve di rischio. La larghezza della suddivisione mostra la quantità di incertezza a ogni livello di percentile per tutte le distribuzioni.
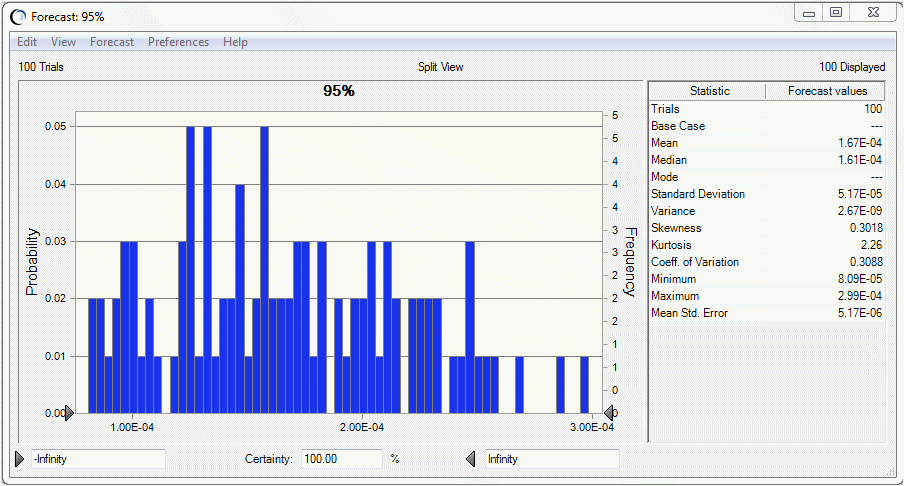
È possibile concentrare l'attenzione su un particolare livello di percentile, ad esempio il novantacinquesimo percentile, visualizzando le statistiche della previsione corrispondente, illustrata nella Figura 9.21, «Statistiche di previsione del novantacinquesimo percentile». Ad esempio, questa figura mostra 100 prove, il numero di novantacinquesimi percentili nella previsione.
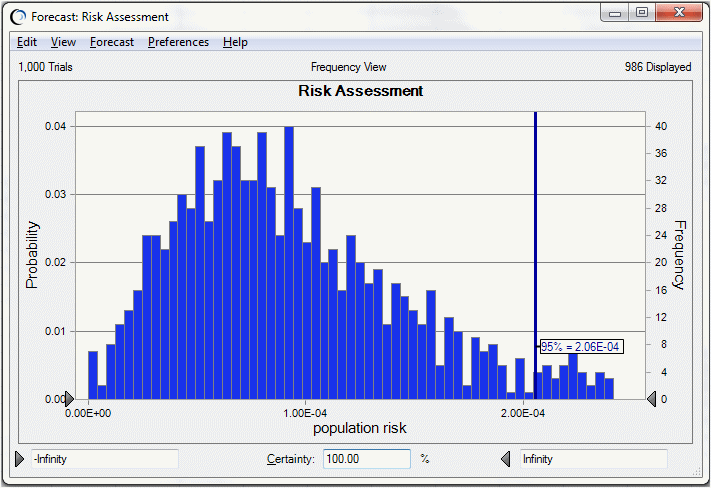
Confrontare i risultati di una simulazione bidimensionale con una simulazione unidimensionale (con incertezza e variabilità combinate tra loro) dello stesso modello di rischio, come illustrato nella Figura 9.22, «Grafico di previsione per una simulazione unidimensionale».
La media dei novantacinquesimi percentili nella Figura 9.21, «Statistiche di previsione del novantacinquesimo percentile», ovvero 1.45E-4, è inferiore al rischio relativo al novantacinquesimo percentile della simulazione unidimensionale illustrata nella Figura 9.22, «Grafico di previsione per una simulazione unidimensionale», ovvero 2.06E-4. Ciò indica la tendenza dei risultati della simulazione unidimensionale a sovrastimare il rischio per la popolazione, specialmente per le distribuzioni fortemente asimmetriche.
Spesso i parametri delle ipotesi sono correlati. Ad esempio, è normale correlare una media più alta con una deviazione standard più alta o una media più bassa con una deviazione standard più bassa. La definizione di coefficienti di correlazione tra distribuzioni di parametri può aumentare la precisione della simulazione bidimensionale. Avendo a disposizione dei dati, ad esempio i pesi corporei di una popolazione, è possibile utilizzare lo strumento Bootstrap per stimare le distribuzioni di campionamento dei parametri e le correlazioni tra di essi. |
Ipotesi di secondo ordine
Alcune ipotesi contengono elementi sia di incertezza che di variabilità. Ad esempio, un'ipotesi può descrivere la distribuzione del peso corporeo in una popolazione, ma i parametri della distribuzione possono essere incerti. Le ipotesi di questo tipo sono denominate ipotesi di secondo ordine (anche variabili casuali di secondo ordine; vedere i riferimenti su Burmaster e Wilson, 1996, nella bibliografia). È possibile modellare questi tipi di ipotesi in Crystal Ball inserendo i parametri di incertezza della distribuzione in celle separate e definendo tali celle come ipotesi. I parametri dell'ipotesi di variabilità vengono quindi collegati alle ipotesi di incertezza mediante riferimenti di cella.
 Per illustrare questo procedimento per il foglio di calcolo Toxic Waste Site.xlsx, procedere come segue.
Per illustrare questo procedimento per il foglio di calcolo Toxic Waste Site.xlsx, procedere come segue.
Inserire i valori
70e10rispettivamente nelle celle G4 e H4.Si tratta della media e della deviazione standard dell'ipotesi Peso corporeo nella cella C4, definita come distribuzione normale.
Definire un'ipotesi per la cella G4 utilizzando una distribuzione normale con una media pari a 70 e una deviazione standard pari a 2.
Definire un'ipotesi per la cella H4 utilizzando una distribuzione normale con una media pari a 10 e una deviazione standard pari a 1.
Inserire i riferimenti a queste celle nell'ipotesi Peso corporeo (Figura 9.23, «Ipotesi che utilizza riferimenti di cella per la media e la deviazione standard»).
Quando si esegue lo strumento per le ipotesi di secondo ordine, l'incertezza dei parametri delle ipotesi viene modellata nella simulazione esterna, mentre la distribuzione dell'ipotesi stessa viene modellata (per diversi set di parametri) nella simulazione interna.