反覆抽樣是一種抽樣技術,可估計預測統計資料或其他樣本資料的可靠度或準確性。典型的方法有賴於數學公式以描述樣本統計的準確性。當統計的抽樣分配未常態分佈或不易找到時,這些典型的方法則難以使用或無效。
透過重覆地抽樣資料並建立每一個抽樣之不同統計資料的分佈,以反覆抽樣分析樣本統計。反覆抽樣 (bootstrap) 一詞源自於「靠自己的努力出人頭地」(to pull oneself up by one’s own bootstraps),因為此方法利用本身統計資料的分佈以分析統計資料的準確性。
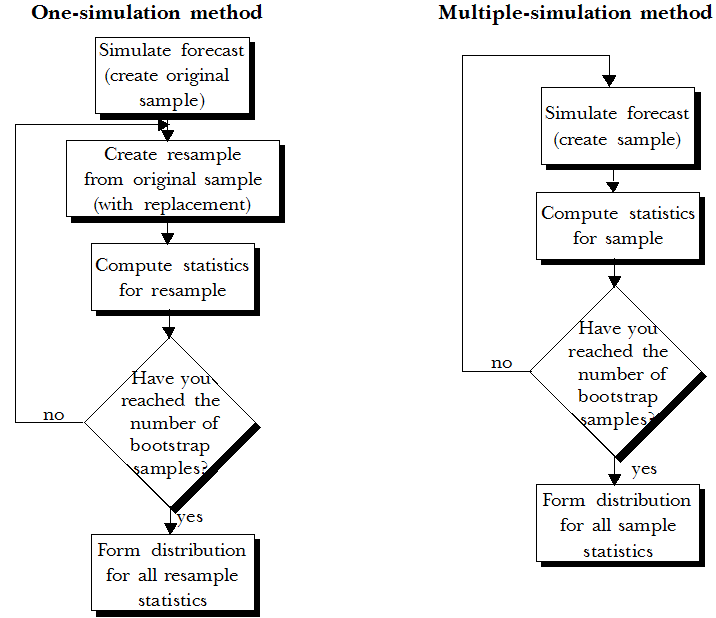
單一模擬方法 — 模擬模型資料一次 (建立原始樣本),然後反覆地抽樣這些模擬試驗 (原始樣本值)。重新抽樣會以替代項目從原始樣本建立一個新樣本。也就是說,它會先將選取的值傳回給樣本,然後再選取其他值,讓選取器可以重複選取相同值。接著,會建立每次重新抽樣所計算得出的統計分佈。此方法假設只有原始模擬資料準確地描繪真實的預測分佈,如果樣本足夠大,這是有可能發生的。此方法不會比多重模擬方法準確,但是其耗費的執行時間明顯比較少。
多重模擬方法 — 重複地模擬模型,然後建立每一個模擬的統計分佈。此方法比單一模擬方法準確,但是其耗費的時間非常多。
因為反覆抽樣技術不會假設抽樣分配是常態分佈的情況,您可以用此方法來估計任何統計資料的抽樣分佈,即使是非常規的統計資料,例如預測的最小值或最大值。您也可以輕鬆地估算複雜的統計資料,例如兩個資料集的相關性係數,或統計資料組合,例如變異數的平均比值。