2.3 下溢

简而言之，下溢发生在以下情况下：算法运算的结果非常小，必须允许存在大于常规情况的舍入误差，才能以其预期的目标格式存储它。

2.3.1 下溢阈值

表 11显示了单精度、双精度和双精度扩展格式的下溢阈值。

表 11  下溢阈值

目标精度 下溢阈值 单精度 最小正规数 最大次正规数 1.17549435e–38 1.17549421e–38 双精度 最小正规数 最大次正规数 2.2250738585072014e–308 2.2250738585072009e–308 四倍精度 最小正规数 最大次正规数 3.3621031431120935062626778173217526e–4932 3.3621031431120935062626778173217520e–4932 双精度扩展 (x86) 最小正规数 最大次正规数 3.36210314311209350626e–4932 3.36210314311209350590e–4932

正次正规数是介于最小正规数和零之间的数。 从最小正规数减去两个与之接近的（正）微小数可以生成次正规数。另外，用最小正正规数除以二也可以生成次正规数。

虽然次正规数本身的精度位数少于正规数，但利用次正规数可以提高微小数字的浮点计算精度。在数学计算中，当生成的正确结果的数量级低于最小正正规数时，就会生成次正规数（而不是返回零），这称为渐进下溢。

要处理这种下溢结果，还有其他几种方法可供使用。一种过去常用的方法是，将这些结果刷新为零。 这种方法称为突然下溢，在引入 IEEE 标准之前，这是大多数大型机的缺省设置。

一方面是获取一种强有力的数学解决方案的愿望，另一方面是创建一种可以有效实施的标准，在权衡这两方面的过程中，起草 IEEE 标准 754 的数学家和计算机设计人员考虑过多种方法。

2.3.2 IEEE 算法如何处理下溢？

IEEE 标准 754 选择渐进下溢作为处理下溢结果的首选方法。这种方法可以归结为定义两种存储值的表示方法：正规数和次正规数。

请记住，正规浮点数的 IEEE 格式：

(-1)^s × (2^(e–bias)) × 1.f

其中 s 是符号位，e 是偏置指数，f 是小数。要完整地指定数字，仅需要存储 s、e 和 f。由于对于正规数，将有效数字的隐式前导位定义为 1，所以需要存储它。

于是，可以存储的最小正正规数具有负的最大数量级指数和全为零的小数。如果前导位是零而不是一，则可以容纳更小的数字。在双精度格式中，由于小数部分的长度为 52 位（约 16 位十进制数字），这可以有效地将最小指数从 10‐308 扩展到 10‐324。这些是次正规数；返回次正规数（而不是将下溢结果刷新为零）就是渐进下溢。

很明显，次正规数越小，其小数中的非零位就越少；生成次正规数结果的计算与正规操作数计算所遵循的相对舍入误差边界不同。但是，有关渐进下溢的主要事实是其使用以下隐含条件：

• 下溢结果不必允许牺牲比普通舍入误差更大的准确性。

• 当结果非常小时，加法、减法、比较和余数运算都总是准确的。

请记住，次正规浮点数的 IEEE 格式：

(-1)^s × (2^(-bias+1)) × 0.f

其中 s 是符号位，偏置指数 e 是零，f 是小数。请注意，隐式 2 的幂偏差比正规格式偏差大一，隐式前导小数位是零。

渐进下溢允许扩展可表示数的下限。它不是使值出行问题的最小限度，而是其他相关的误差。算法使用的是较其他系统误差界限更小的次正规数。下一节将介绍渐进下溢的数学根据。

2.3.3 为什么使用渐进下溢？

次正规数的用途不是为了完全避免下溢/溢出，这与其他一些数学算法模型是不同的。次正规数使人们不再担心下溢会引起各种计算问题，通常是在执行加法后再执行乘法。有关更详细的讨论，请参见 James Demmel 编著的《Underflow and the Reliability of Numerical Software》和 S. Linnainmaa 编著的《Combating the Effects of Underflow and Overflow in Determining Real Roots of Polynomials》。

在算法中使用次正规数，在执行加法或减法运算时，就不会出现未捕获的下溢（这意味着牺牲准确性）了。如果 x 和 y 是 2 以内的因子，则 x – y 是没有误差的。对于一些需要有效提高关键位置工作精度的算法来说，这是非常重要的。

另外，渐进下溢意味着下溢引起的误差不会比一般的舍入误差更糟糕。相对于其他处理下溢的方法，这种说法更有说服力，从而，这一事实成为使用渐进下溢的最佳根据。

2.3.4 渐进下溢的误差属性

在大多数情况下，浮点结果都是舍入的：

computed result = true result + round-off

用来表示误差大小的一种简便尺度称为最后位置单元，简称 ulp。用标准表示法表示的浮点数小数的最低有效位即是其最后一位。用这一位表示的值（例如，除了这一位外，表示法完全相同的两个数字绝对差值）是该数字的最后位置单元。如果计算结果是通过将真正结果舍入到最接近的可表示数字得到的，则显然，舍入误差不会大于计算结果最后位置单元的一半。换而言之，在采用就近舍入模式的 IEEE 算法中，其计算结果如下所示：

0 ≤ |舍入| ≤½ulp

请注意，ulp 是相对值。如果数字非常大，其 ulp 本身就非常大，而如果数字非常小，其 ulp 本身也非常小。将 ulp 表示为函数，这种关系会更明显：ulp(x) 表示浮点数 x 最后位置单元。

另外，浮点数的 ulp 还取决于该数字的表示精度。例如，表 12显示了上述四个浮点格式的 ulp(1) 值：

表 12  四种不同精度的 ulp(1)

精度 值 单精度 ulp(1) = 2^-23 ~ 1.192093e-07 双精度 ulp(1) = 2^-52 ~ 2.220446e-16 双精度扩展 (x86) ulp(1) = 2^-63 ~ 1.084202e-19 四倍精度 ulp(1) = 2^-112 ~ 1.925930e-34

请记住，只有有限数字集才能用计算机算法准确表示。随着数字的数量级的降低并接近零，相邻可表示数字之间的差距会变小。相反，当数字的数量级增加时，相邻可表示数字之间的差距将变大。

例如，假定您要使用只有三个精度位的二进制算法。那么，在任意两个 2 的幂之间，有 2³ = 8 个可表示数字，如下图所示。

图 6  数轴

数轴显示了数字之间的差距是随着指数增加而加倍增加的。

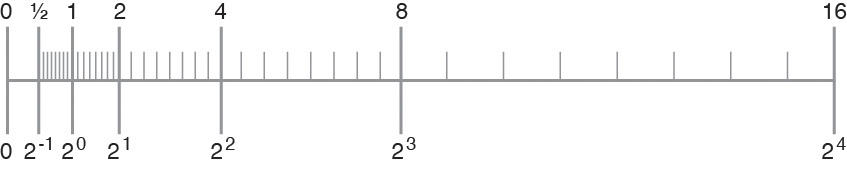
在 IEEE 单精度格式中，两个最小正次正规数之间的差大约是 10^{- 45}，而两个最大有限数之间的数量级差大约是 10³¹！

在表 13中，nextafter(x,+∞) 表示在沿着数轴向 +∞ 移动的过程中，x 之后的下一个可表示数字。

表 13  可表示的单精度格式浮点数之间的差距

x nextafter(x, +·) 差距 0.0 1.4012985e–45 1.4012985e–45 1.1754944e–38 1.1754945e–38 1.4012985e–45 1.0 1.0000001 1.1920929e–07 2.0 2.0000002 2.3841858e–07 16.000000 16.000002 1.9073486e–06 128.00000 128.00002 1.5258789e–05 1.0000000e+20 1.0000001e+20 8.7960930e+12 9.9999997e+37 1.0000001e+38 1.0141205e+31

所有传统的可表示浮点数集都有一个属性，不准确结果的最差情况是：引入一个不大于计算结果中可表示相邻数字之间的距离的误差。将次正规数加到可表示集上并实施渐进下溢时，不准确结果或下溢结果的最差情况是：引入一个不大于计算结果中可表示相邻数字之间的距离的误差。

尤其是，在零与最小正规数之间的区域，任意两个相邻数字之间的距离等于零与最小次正规数之间的距离。 利用次正规数，可以避免出现以下情况：引入的舍入误差大于最近可表示数字之间的距离。

由于没有计算引起的舍入误差会大于与计算结果任意可表示相邻数字的距离，所以许多强大的算法环境都符合以下三条属性：

• x ≠ y 当且仅当 x – y ≠ 0

• (x – y) + y ≈ x，在 x 和 y 二者中较大者的舍入误差内

• 1/(1/x) ≈ x，当 x 是正规化数时，表示 1/x ≠ 0，甚至对于最大正规化 x 也是如此

另一种下溢方案是突然下溢，它是将下溢结果刷新为零。 只要 x – y 出现下溢，突然下溢就会违反第一条和第二条属性。另外，当 1/x 出现下溢时，突然下溢还将违反第三条属性。

我们用 λ 表示最小正正规化数，也称为下溢阈值。 这样，就可以用 λ 来比较渐进下溢和突然下溢的误差属性。

渐进下溢：|误差| < ½λ 的 ulp

突然下溢：|误差| ≈ λ

用 λ 最后位置单元的一半与 λ 本身存在着显著的差别。

2.3.5 有关渐进下溢与突然下溢的两个示例

以下是两个有名的数学示例。第一个示例是计算内积的代码。

sum = 0; 
for (i = 0; i < n; i++) {
 sum = sum + a[i] * y[i]; 
} 
return sum;

利用渐进下溢，结果的精确度为舍入的精确度。在突然下溢中，可能会在几乎所有数字中传递看上去合理实则错误的微小非零和。然而，公平来讲，我们必须承认，为了避免出现这些问题，聪明的编程人员在预见到会出现微小值影响精确度时，会扩大其计算范围。

第二个示例源于复数商，不适用于缩放：

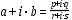假定 |r / s|≤1

。

可以显示出，虽然进行了舍入，但得出的复数结果与准确结果之间的差不大于以下条件下得出的结果与准确结果之间的差：p + i · q 和 r + i · s 每个值的误差都不大于几个 ulp。除了当 a 和 b 都出现下溢外，这种误差分析是面向下溢的，误差是通过以下值的几个 ulp 来界定的：|a + i · b|。将下溢刷新为零时，就不会得出这样的结论。

这种计算复数商的算法非常强大，并且适用于渐进下溢时的误差分析。要在突然下溢的情况下找到同样强大、易于分析且有效的计算复数商的算法是不可能的。在突然下溢的情况下，考虑低级、复杂细节的麻烦从浮点环境的实现工具转移到了用户那里。

利用渐进下溢成功解决但利用突然下溢却失败的问题类要比支持使用突然下溢的人想像的多。许多常用的数值技术都无法成功解决此类问题：

• 线性方程求解

• 多项式方程求解

• 数值积分

• 收敛性加速

• 复数除法

2.3.6 下溢有问题吗？

尽管举了以上示例，但下溢算法基本上没有任何问题，因此，我们有什么理由不使用它呢？事实上，这一观点是不言而喻的。

如果没有渐进下溢，用户程序需要对隐含的精确度阈值特别敏感。 例如，在单精度计算中，如果计算的某些部分发生了下溢，在使用突然下溢的情况下，会将下溢结果替换为 0，则所能保证的精确度只能达到大约 10^-31，而不是 10^-38，即单精度指数的一般下限。

这意味着，编程人员需要在接近不准确阈值时实施自己的检测方法，否则，将不得不放弃寻求强大、稳定的实施其算法的努力。

我们可以缩放某些算法，这样，在接近零的限定区域将不会执行计算。不过，缩放算法和检测不准确阈值都比较困难且耗时，即使对于大多数数据而言也是没有必要的。