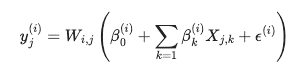地理的重み付け回帰
地理的加重回帰(GWR)モデルは、空間異種性の存在下で使用され、これはリージョン変動の兆候として識別できます。
GWRモデルは、データセット内のすべての観測に対して局所線形回帰モデルを作成します。 近傍の観測からターゲット変数と説明変数を取り込み、独立変数と従属変数間の関係を近傍性によって変えることができます。
次に、GWRモデルの式を示します:
前述の方程式で、Wは空間加重マトリックス、yj(i)は観測jのターゲット変数の推定です(ロケーションi)。
GWRRegressorクラスは、データセット内のすべてのサンプルのローカル線形回帰をトレーニングし、指定された帯域幅内に収まるロケーションの依存変数および独立変数を組み込みます。
次の表に、GWRRegressorクラスの主なメソッドを示します。
| メソッド | 説明 |
|---|---|
fit |
アルゴリズムには帯域幅が必要です。この帯域幅は、ユーザーがbandwidthパラメータを使用するか、spatial_weights_definitionパラメータを指定して設定できます。
bandwidthパラメータもspatial_weights_definitionパラメータも定義されていない場合、帯域幅はジオメトリに基づいて内部的に推定されます。
|
predict |
予測を行うために、GWRは、トレーニング・データからの隣接する観測値を使用して、予測セット上の各観測のモデルを作成します。 次に、これらのモデルを使用してターゲット変数を見積もります。 |
fit_predict |
トレーニング・データを使用して、fitおよびpredictメソッドを順番にコールします。
|
score |
指定されたデータのR平方統計を返します。 |
詳細は、「Oracle Spatial AI Python APIリファレンス」のGWRRegressorクラスを参照してください。
次の例では、block_groups SpatialDataFrameおよびGWRRegressorを使用して、ターゲット変数MEDIAN_INCOMEを予測するモデルをトレーニングします。 トレーニング・セットを使用してモデルをトレーニングし、テスト・セットを使用してターゲット変数の予測を行い、R平方統計を取得します。
from oraclesai.preprocessing import spatial_train_test_split
from oraclesai.weights import DistanceBandWeightsDefinition
from oraclesai.regression import GWRRegressor
from oraclesai.pipeline import SpatialPipeline
from sklearn.preprocessing import StandardScaler
# Define target and explanatory variables
X = block_groups[['MEDIAN_INCOME', 'MEAN_AGE', 'MEAN_EDUCATION_LEVEL', 'HOUSE_VALUE', 'INTERNET', 'geometry']]
# Use a referenced coordinate system
X = X.to_crs("epsg:3857")
# Define training and test sets
X_train, X_test, _, _, _, _ = spatial_train_test_split(X, y="MEDIAN_INCOME", test_size=0.1, random_state=32)
# Define the spatial weights
weights_definition = DistanceBandWeightsDefinition(threshold=10000)
# Create an instance of GWR passing the spatial weights
gwr_model = GWRRegressor(spatial_weights_definition=weights_definition)
# Add the regressor to a pipeline along with a preprocessing step
gwr_pipeline = SpatialPipeline([('scale', StandardScaler()), ('gwr_regression', gwr_model)])
# Train the model specifying the target variable
gwr_pipeline.fit(X_train, "MEDIAN_INCOME")
# Print the predictions with the test set
gwr_predictions_test = gwr_pipeline.predict(X_test.drop(["MEDIAN_INCOME"])).flatten()
print(f"\n>> predictions (X_test):\n {gwr_predictions_test[:10]}")
# Print the score with the test set
gwr_r2_score = gwr_pipeline.score(X_test, y="MEDIAN_INCOME")
print(f"\n>> r2_score (X_test):\n {gwr_r2_score}")プログラムの出力は次のようになります:
>> predictions (X_test):
[111751.58871802 123406.64795915 25850.4248602 23565.60954771
180171.51825151 47052.37667604 118800.80714934 31067.07113894
62079.81316461 30673.82128591]
>> r2_score (X_test):
0.6942389040067138summaryプロパティには、OLSおよびGWRモデルの統計が含まれます。 推定パラメータについては、すべてのローカル・モデルの平均値が表示されます。
===========================================================================
Model type Gaussian
Number of observations: 3093
Number of covariates: 5
Global Regression Results
---------------------------------------------------------------------------
Residual sum of squares: 1816309978579.363
Log-likelihood: -35614.052
AIC: 71238.104
AICc: 71240.132
BIC: 1816309953761.425
R2: 0.635
Adj. R2: 0.634
Variable Est. SE t(Est/SE) p-value
------------------------------- ---------- ---------- ---------- ----------
X0 69761.518 436.080 159.974 0.000
X1 2555.817 564.452 4.528 0.000
X2 5613.607 843.158 6.658 0.000
X3 19204.921 602.745 31.862 0.000
X4 10031.929 637.215 15.743 0.000
Geographically Weighted Regression (GWR) Results
---------------------------------------------------------------------------
Spatial kernel: Fixed bisquare
Bandwidth used: 10000.000
Diagnostic information
---------------------------------------------------------------------------
Residual sum of squares: 1247690194588.343
Effective number of parameters (trace(S)): 117.770
Degree of freedom (n - trace(S)): 2975.230
Sigma estimate: 20478.262
Log-likelihood: -35033.321
AIC: 70304.183
AICc: 70313.751
BIC: 71021.184
R2: 0.749
Adjusted R2: 0.739
Adj. alpha (95%): 0.002
Adj. critical t value (95%): 3.075
Summary Statistics For GWR Parameter Estimates
---------------------------------------------------------------------------
Variable Mean STD Min Median Max
-------------------- ---------- ---------- ---------- ---------- ----------
X0 62341.157 12808.790 -66225.562 64262.819 94371.705
X1 2998.233 3153.236 -12716.566 3338.876 18130.392
X2 10539.611 7148.106 -7226.756 9336.382 70067.037
X3 16577.403 9934.050 -9579.528 16819.683 47874.385
X4 9771.744 4232.729 1656.213 9326.487 44417.212
===========================================================================