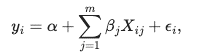OLSを使用した空間診断
空間モデリングの最初のステップは、多線形性、正規分布バイアス、空間異種性、空間依存性の分析など、空間診断を行うことです。 これはOrdinary Least Squre (OLS)モデルを使用して実行できます。
OLSアルゴリズムは、トレーニング・セットの平均平方誤差(MSE)を最小限にして新しい値を予測する行に適合します。 通常の線形回帰の式は次のようになります:
前述の算式:αはインターセプト・パラメータまたは定数パラメータ、βはパラメータのベクトルで、各変数がターゲット変数yとどの程度関連しているか、εiがエラーを表すかに関する情報を提供します。 OLSモデルをトレーニングする際の目標は、パラメータαおよびβを見積り、Xの新しい値についてyの値を予測することです。
空間AIのOLSRegressorクラスは、一般的なOLSモデルにspatial_weights_definitionパラメータを追加します。これにより、モデルのトレーニング後に空間統計を取得できます。 これらの統計は、空間依存性または空間異種性の存在を識別し、別のアルゴリズムが必要かどうかを判断するのに役立ちます。 したがって、OLSRegressorは、ユーザーがデータを診断して特別な空間関係があるかどうかを確認できるようにすることを目的としています。この関係は、特定のタスクに使用する空間回帰アルゴリズムの決定に役立ちます。 統計の詳細は、「空間回帰のメトリック」を参照してください。
次の表に、OLSRegressorクラスの主なメソッドを示します。
| メソッド | 説明 |
|---|---|
fit |
spatial_weights_definitionパラメータが指定されている場合、OLSモデルを指定されたトレーニング・データからトレーニングし、空間統計を取得します。
|
predict |
トレーニング済パラメータを使用して、指定されたデータのターゲット変数を見積もります。 |
fit_predict |
トレーニング・データを使用して、fitおよびpredictメソッドを順番にコールします。
|
score |
指定されたデータのR平方統計。 |
詳細は、「Oracle Spatial AI Python APIリファレンス」のOLSRegressorクラスを参照してください。
次の例では、block_groups を使用して、SpatialDataFrame spatial_weights_definitionパラメータを定義するOLSモデルを作成します。 モデルのトレーニング後、predictおよびscoreメソッドをコールします。 最後に、空間統計を含むモデルのサマリーが出力されます。
from oraclesai.preprocessing import spatial_train_test_split
from oraclesai.regression import OLSRegressor
from oraclesai.weights import KNNWeightsDefinition
# Define the training and test set.
X = block_groups[["MEDIAN_INCOME", "MEAN_AGE", "HOUSE_VALUE", "INTERNET", "geometry"]]
X_train, X_test, _, _, _, _ = spatial_train_test_split(X, y="MEDIAN_INCOME", test_size=0.2)
# Create the OLSRegressor defining the spatial_weights
spatial_ols_model = OLSRegressor(KNNWeightsDefinition(k=10))
# Train the model and specify the target variable
spatial_ols_model.fit(X_train, "MEDIAN_INCOME")
# Print the predictions of the test set
ols_predictions_test = spatial_ols_model.predict(X_test.drop(["MEDIAN_INCOME"])).flatten()
print(f"\n>> predictions (X_test):\n {ols_predictions_test[:10]}")
# Print the R-squared score of the test set
ols_r2_score = spatial_ols_model.score(X_test, y="MEDIAN_INCOME")
print(f"\n>> r2_score (X_test):\n {ols_r2_score}")
# Prints a summary of the model
print(spatial_ols_model.summary)プログラム出力には次のものが含まれます:
predictメソッドは、テスト・セットに対するターゲット変数の推定値を返します。scoreメソッドは、テスト・セットからモデルのR平方メトリックを返します。summaryプロパティは、複数の統計および各説明変数に関連付けられたパラメータを提供します。 また、spatial_weights_definitionパラメータに基づく空間統計も含まれます。
>> predictions (X_test):
[84333.95556955 88819.9988673 52445.40662329 66192.50638257
66613.63752196 53802.16810985 65151.54020825 29424.26087764
37296.49147829 85676.22038382]
>> r2_score (X_test):
0.6009367861353069
REGRESSION
----------
SUMMARY OF OUTPUT: ORDINARY LEAST SQUARES
-----------------------------------------
Data set : unknown
Weights matrix : unknown
Dependent Variable : dep_var Number of Observations: 2750
Mean dependent var : 70051.6531 Number of Variables : 4
S.D. dependent var : 40235.8666 Degrees of Freedom : 2746
R-squared : 0.6385
Adjusted R-squared : 0.6381
Sum squared residual:1608810557754.003 F-statistic : 1616.7374
Sigma-square :585874201.658 Prob(F-statistic) : 0
S.E. of regression : 24204.838 Log likelihood : -31659.426
Sigma-square ML :585022021.001 Akaike info criterion : 63326.852
S.E of regression ML: 24187.2285 Schwarz criterion : 63350.529
------------------------------------------------------------------------------------
Variable Coefficient Std.Error t-Statistic Probability
------------------------------------------------------------------------------------
CONSTANT -61472.5132881 3718.3646558 -16.5321368 0.0000000
MEAN_AGE 798.8367637 94.5268152 8.4509011 0.0000000
HOUSE_VALUE 0.0558167 0.0014696 37.9805274 0.0000000
INTERNET 85961.1765144 3867.7192944 22.2252883 0.0000000
------------------------------------------------------------------------------------
REGRESSION DIAGNOSTICS
MULTICOLLINEARITY CONDITION NUMBER 20.388
TEST ON NORMALITY OF ERRORS
TEST DF VALUE PROB
Jarque-Bera 2 955.683 0.0000
DIAGNOSTICS FOR HETEROSKEDASTICITY
RANDOM COEFFICIENTS
TEST DF VALUE PROB
Breusch-Pagan test 3 1198.122 0.0000
Koenker-Bassett test 3 526.447 0.0000
DIAGNOSTICS FOR SPATIAL DEPENDENCE
TEST MI/DF VALUE PROB
Moran's I (error) 0.2395 29.493 0.0000
Lagrange Multiplier (lag) 1 426.035 0.0000
Robust LM (lag) 1 4.674 0.0306
Lagrange Multiplier (error) 1 854.940 0.0000
Robust LM (error) 1 433.579 0.0000
Lagrange Multiplier (SARMA) 2 859.614 0.0000
================================ END OF REPORT =====================================