Von automatischen Insights generierte Visualisierungstypen
Automatische Insights generieren verschiedene Visualisierungstypen, die spezifische Einblicke in Ihre Daten liefern. Jede dieser Visualisierungen verwendet andere Spalten aus Ihren Daten. Die Rangfolge hängt vom Wert der Insight im Kontext Ihrer Daten ab.
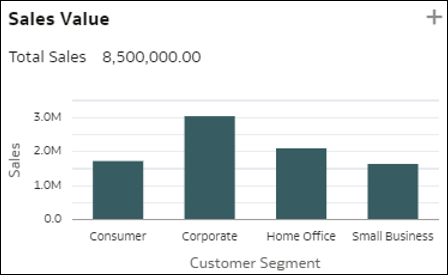
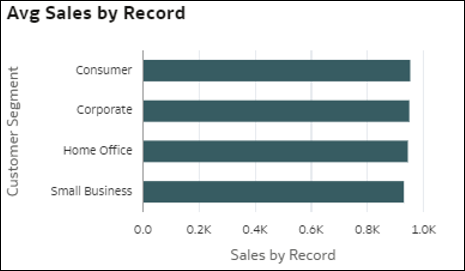
- Dimensionsaufschlüsselungen: Diese Visualisierungen aggregieren einen Kennzahlwert für die verschiedenen Elemente einer Dimension in Ihren Daten. So erhalten Sie einen schnellen Überblick darüber, wie die ausgewählte Metrik in Bezug auf eine gegebene Dimension verteilt ist. Bei der Kennzahl kann es sich um eine Metrik aus Ihrem Dataset, eine Datensatzanzahl oder einen durchschnittlichen Wert der Metrik je Datensatz handeln.
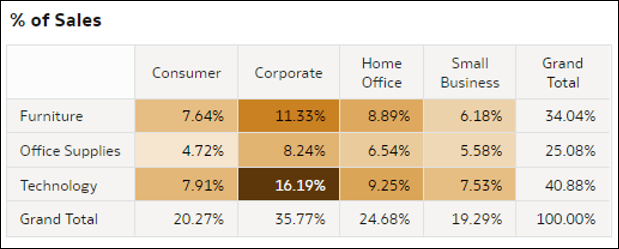
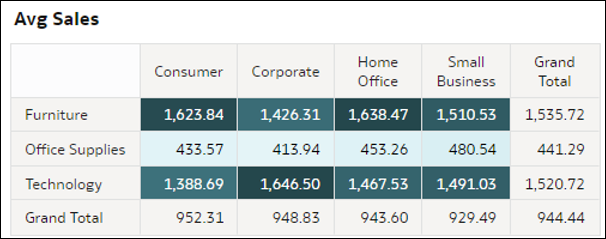
- Heatmap-Pivot-Tabellen: Diese Visualisierungen aggregieren einen Kennzahlwert für die Schnittmengen zweier Dimensionen in Ihren Daten. Jede Zelle in der Pivot-Tabelle stellt eine Schnittmenge der Elemente der beiden ausgewählten D2-Dimensionen dar. Mit diesen Visualisierungen können Sie schnell verstehen, wo sich die höchsten Werte für die Kennzahl befinden, indem Sie die dunkelsten Zellen in den Tabellen betrachten. Kennzahlen können in dieser Visualisierung eine Metrik aus Ihrem Dataset, eine Datensatzanzahl, ein durchschnittlicher Wert einer Metrik je Datensatz oder ein Prozentsatz sein, der eine beliebige dieser Optionen darstellt (Gesamtsumme rechts 100%).
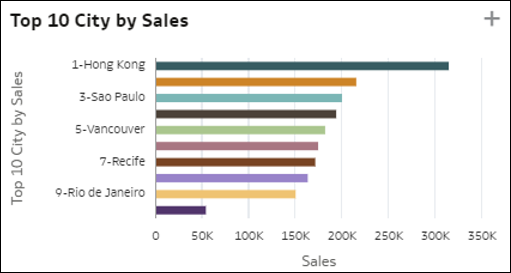
- Top 10 Einzelne: Diese Visualisierung zeigt die höchstwertigen Elemente einer Dimension nach Wert der Kennzahl in Ihrem Dataset in absteigender Ordnung. Der letzte Balken im Diagramm zeigt den durchschnittlichen Wert der Kennzahl für alle Elemente, die nicht zu den Top 9 gehören. Das ist der durchschnittliche Wert von M1 für alle Einzelelemente, die nicht in der Top-Rangliste enthalten sind. Diese Information zeigt, wie groß der Vorsprung der ranghöchsten Einzelelemente vor dem Durchschnitt des Rests der Population ist.
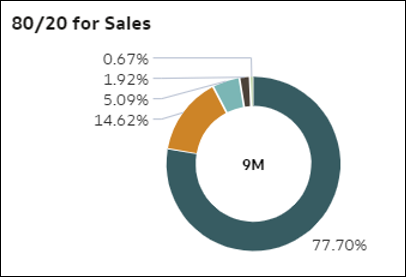
- 80/20: Diese Visualisierung zeigt für eine gegebene Kennzahl, welches Gewicht die Datensätze in den Top 20% Ihrer Daten im gesamten Dataset haben. Die Top 20% werden auf der Basis der Detailzeilen in Ihrem Dataset berechnet. Das Ringdiagramm zeigt die Bedeutung der wichtigsten Einzelelemente in Ihren Daten für die Kennzahl. Die Bögen des Ringdiagramms stellen Quintile von Datensätzen dar, also aufeinanderfolgende Abschnitte von je 20% der Datensätze, absteigend geordnet nach Zeilenanzahl (wichtigste 20% der Einzelelemente, dann die nächsten 20% usw.). Die Größe der Bögen stellt den aggregierten Gesamtwert der Kennzahl für jedes Quintil dar.
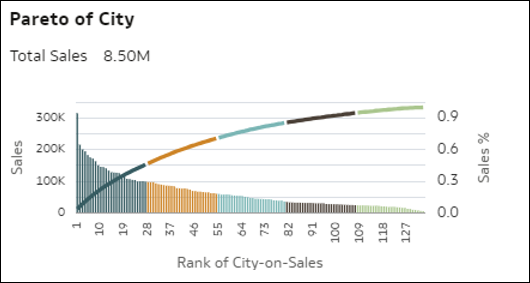
- Pareto: Diese Pareto-Diagrammvisualisierung zeigt jedes Element einer Dimension (mittlere Kardinalität), absteigend geordnet nach Wert einer Kennzahl. Jeder Balken stellt diese Kennzahl für ein Element dar, und die Linie stellt den kumulativen Prozentsatz des Kennzahlwertes dar (mit Summe 1,0 = 100%), wenn die Anteile der Elemente kumulativ addiert werden. Ein Pareto-Diagramm rückt die Bereiche mit dem größten relativen Wert oder der größten Häufigkeit in den Fokus.
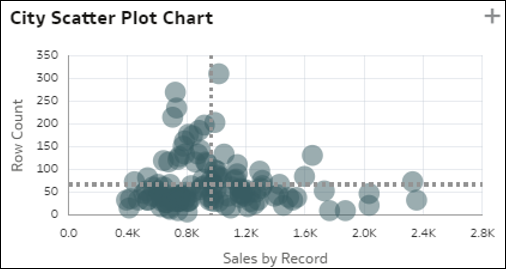
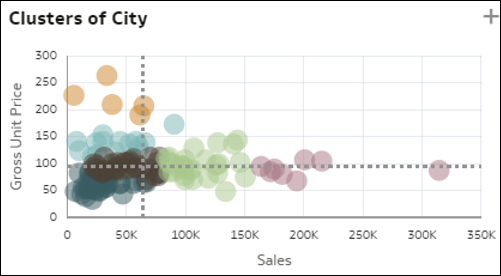
- Streudiagramme und Cluster. Die Streudiagrammvisualisierung zeigt alle Elemente einer Dimension (mittlere Kardinalität) in einem Raster mit zwei verschiedenen Kennzahlen aus Ihren Daten für die Achsen. Jede Kennzahl ist nach dem durchschnittlichen Einheitswert abgestuft. Die Streuung dieser Datensätze und die potenziellen Ausreißer bieten interessante Einblicke in Ihre Dimensionselemente. Dieses Diagramm gibt Ihnen einen schnellen Einblick, wie gut die beiden Metriken bei den B1-Elementen miteinander korrelieren, und Sie können leicht erkennen, welche Elemente in welchen Quadranten fallen. Eine Variante des Streudiagramms zeigt ein automatisches Clustering Ihrer Datensätze in sechs zusammenhängende Gruppen.
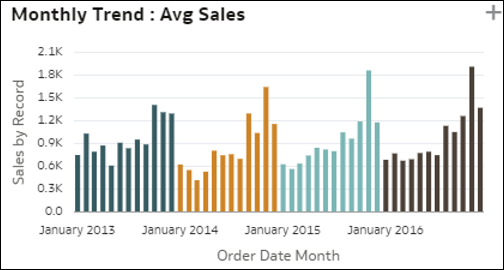
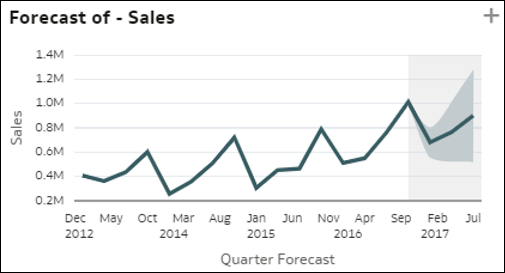
- Einfache Trendbalkendiagramme: Diese Visualisierung stellt die trendbasierte Entwicklung einer Kennzahl über eine Zeitspalte in Ihrem Dataset dar. Sie können interessante Trendmuster wie Wachstum oder Rückgang aufzeigen. Die Kennzahl kann eine Metrik aus Ihrem Dataset, eine Datensatzanzahl oder ein Durchschnittswert einer Kennzahl pro Datensatz sein. Die gleiche Insight kann auch mit einer zusätzlichen Prognoselinie rechts im Diagramm angezeigt werden.
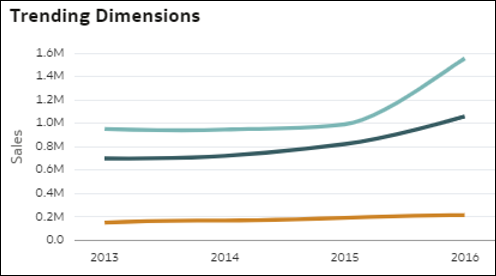
- Trendvergleich nach Dimension: Diese Visualisierung vergleicht, wie sich der Wert einer Kennzahl für jedes Element einer Dimension im Zeitverlauf entwickelt hat. Jede Linie zeigt die Entwicklung einer Kennzahl für ein gegebenes Element der Dimension. Wachstum oder Rückgang des Kennzahlwertes sind nicht bei allen Elementen in der Dimension einheitlich, was eine interessante Insight darstellen kann: Welches Element entwickelt sich anders als die anderen?
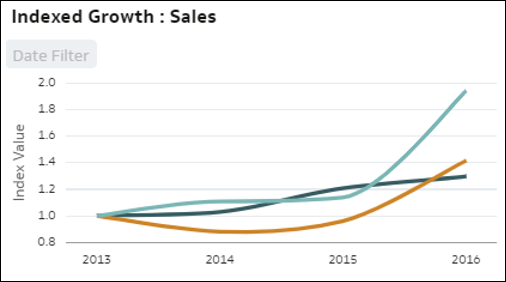
- Indexierter Trendvergleich: Diese Visualisierung vergleicht das relative Wachstum einer Kennzahl im Zeitverlauf für jedes Element einer Dimensionsspalte in Ihren Daten. Jede Linie stellt ein Element der Dimension dar, wobei für einen anfänglichen Zeitraum ein Basisindexwert von 1,00 festgelegt wird. Die Entwicklung im Zeitverlauf zeigt den relativen Wert in den Folgezeiträumen relativ zum anfänglichen Indexwert von 1,00. Die Verwendung von indexierten statt absoluten Werten ermöglicht einen guten Vergleich zwischen verschiedenen Trends, da die Linien die wirkliche relative Entwicklung zeigen und so das Wachstum aller Elemente direkt vergleichen. Beim Betrachten der absoluten Werte von Metriken anstelle der indizierten Werte, ist es aufgrund der Abweichungen in den Werten oft unmöglich, Wachstum oder Rückgang richtig zu vergleichen. Durch die Verwendung eines Indexwertes ist das tatsächliche relative Verhalten leichter zu erkennen.
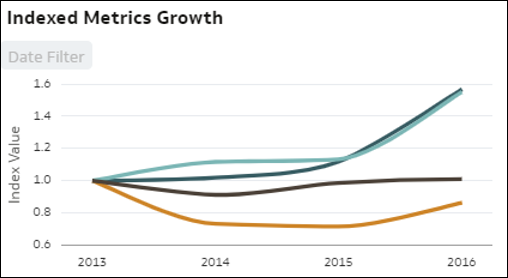
- Indexierter Trend nach Kennzahl: Diese Visualisierung vergleicht die relative Entwicklung mehrerer Kennzahlen im Dataset im Zeitverlauf. Das Liniendiagramm visualisiert den indexierten Wert verschiedener Metriken im Dataset im Zeitverlauf. Jede Linie stellt eine Kennzahl dar. Die Verwendung von indexierten statt absoluten Werten ermöglicht einen guten Vergleich zwischen verschiedenen Trends, da die direkte Betrachtung der absoluten Werte der Metriken den Vergleich zwischen Wachstum oder Rückgang erschwert. Ein Anfangsindexwert (1,00) aller Metriken wird für einen Anfangszeitraum festgelegt, und die Linie zeigt die relative Entwicklung jeder Metrik im Vergleich zu ihrem Ausgangspunkt im Diagramm (Index).
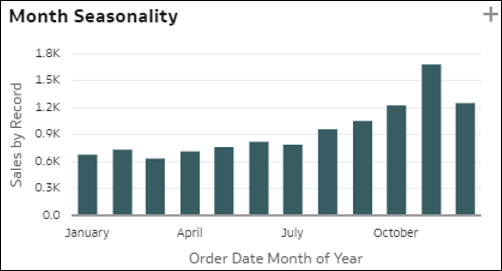
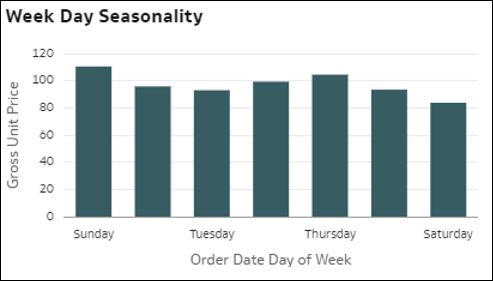
- Saisonalität: Die Balken in dieser Visualisierung stellen die Verteilung einer Kennzahl nach Monat im Jahr, Tag im Monat oder Wochentag eines Zeitobjekts in Ihrem Dataset dar. Das ist ein Hinweis auf eine mögliche Saisonalität des Verhältniswertes im Monatsverlauf. Anhand von Saisonalitätsdiagrammen lassen sich wiederkehrende Muster in Daten über bestimmte Zeiträume hinweg erkennen. Das kann entscheidend zum Verständnis der saisonalen Schwankung von Kennzahlwerten beitragen.
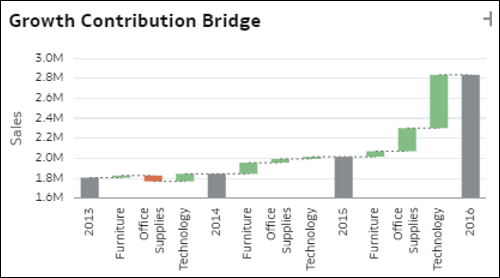
- Wasserfalldiagramm der Elementbeiträge: Dieses Wasserfalldiagramm zeigt den Beitrag jedes Elements einer Dimension in Ihrem Dataset zur Variation eines Kennzahlwertes im Zeitverlauf. Es gibt Aufschluss darüber, welche Elemente in einem Zeitraum am stärksten zu einem Wachstum oder Rückgang beigetragen haben. Jeder graue Balken in dem Diagramm stellt den Gesamtwert einer Kennzahl für einen Zeitraum T1 dar. Die grünen und roten Balken zwischen zwei Zeiträumen zeigen, welche Elemente gewachsen oder zurückgegangen sind. So wird deutlich, wie sie zur Gesamtveränderung beigetragen haben.
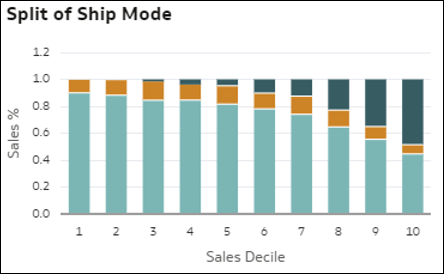
- Aufschlüsselung der Dimensionselemente (Mix) vs. Kennzahlwert: Diese Visualisierung gibt Aufschluss über den (aufgeschlüsselten) Mix aller Elemente einer Dimension in Ihren Daten bei wachsendem Kennzahlwert. Die Balken stellen die relativen Werte der Kennzahl dar: Dezil 1 = niedriger Kennzahlwert nach Datensatz (die ersten 10% der Datensätze), Dezil 2 = zweite 10% usw. bis Dezil 10 = hoher Kennzahlwert nach Datensatz. In jedem Balken zeigen die Farben den Anteil jedes Elements der Dimension am Gesamtwert der Kennzahl für das jeweilige Dezil. Dadurch wird deutlich, dass sich die Struktur des Elementmix verändert, wenn sich der Kennzahlwert verändert.
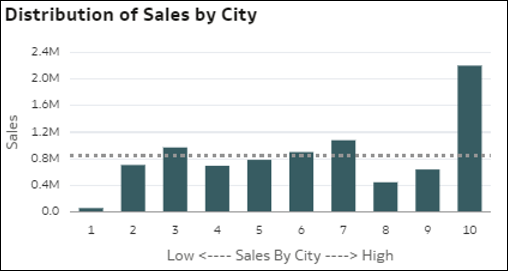
- Histogramm einer Kennzahl nach Datensatz-Bins: Diese Visualisierung zeigt, wie eine Kennzahl auf die Bins einer anderen Metrik verteilt ist. Die Balken in dem Diagramm zeigen die Aggregation der Kennzahl, und jeder Balken stellt einen Bin für eine Kennzahl dar: Bin 1 = niedriger Kennzahlwert nach Datensatz und Bin 10 = hoher Kennzahlwert nach Datensatz.
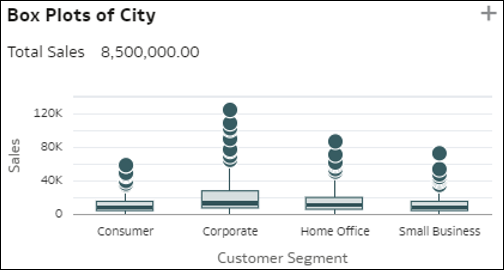
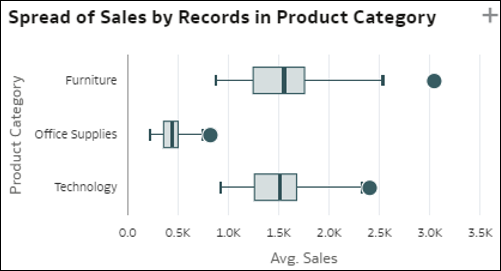
- Boxplot der Dimensionselemente: Diese Boxplotvisualisierung vergleicht die Streuung der Einzelelemente einer Dimension D1 (mittlere Kardinalität) in Ihren Daten (Punkten) mit dem Wert einer Kennzahl. Dieser wird für jedes Element der anderen Dimension D2 (Balken) dargestellt. Die vertikalen Linien im Boxplot zeigen die verschiedenen Elemente von D2. Jeder Punkt innerhalb einer Linie repräsentiert ein einzelnes Element von D1. Die Y-Achse gibt den durchschnittlichen Wert der Metrik für jedes Element an. Jeder Balken stellt drei Werte für das Element von D2 dar: den Wert für das erste Quartil unten im Balken, den durchschnittlichen Wert in der Mitte und das dritte Quartil oben. Diese Visualisierung dient dazu, die Streuung der Datensätze in einer Dimension D1 zu erkennen und Unterschiede in dieser Verteilung zwischen Elementen einer Dimension D2 zu vergleichen.
- Streuung von Datensatzwerten nach einer Dimension: Diese Diagrammvisualisierung zeigt die Streuung (Dispersion) von Datensätzen nach Wert einer Kennzahl für jedes der Elemente einer Dimension (Balken). Die X-Achse zeigt den durchschnittlichen Wert der Kennzahl nach Datensatz. Die Punkte in jedem der Balken stellen zufällige Gruppen granularer Datensätze aus dem Dataset dar. Diese Visualisierung gibt Aufschluss darüber, wie sich die Streuung zwischen verschiedenen Elementen einer Dimension (verschiedenen horizontalen Balken auf der Visualisierung) unterscheiden kann.
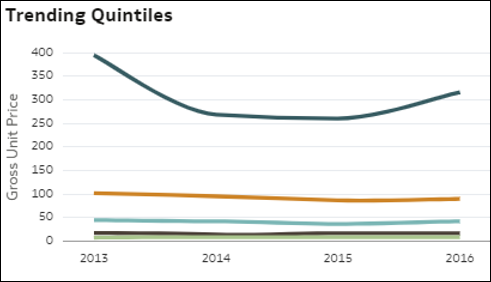
- Quintiltrendvergleich Diese Visualisierung vergleicht, wie sich jede der 20%-Gruppen von Datensätzen (Quintilen) in den Daten (sortiert nach dem Wert einer Kennzahl) von den Top-Performern bis zu den Bottom-Performern im Zeitverlauf entwickelt hat. War das Wachstum oder der Rückgang in den oberen und unteren Gruppen einheitlich oder nicht? Bei welcher Populationsgruppe entwickelt sich die Kennzahl anders? Jede Linie in dem Diagramm stellt ein Quintil dar und zeigt die Entwicklung des Wertes von M1 im Zeitverlauf. Quintile sind Gruppen von 20% der Datensätze im Dataset. Sie sind absteigend nach Kennzahlwert geordnet: Die 20% der Datensätze mit den höchsten Kennzahlwerten, gefolgt von den nächsten 20% usw.