Typy wizualizacji generowanych przez automatyczne spostrzeżenia
Funkcja automatycznych spostrzeżeń generuje różnego typu wizualizacje, które przedstawiają konkretne spostrzeżenia dotyczące danych. Każda z tych wizualizacji wykorzystuje różne kolumny z danych i jest uszeregowana w zależności od wartości danego spostrzeżenia w kontekście aktualnych danych.
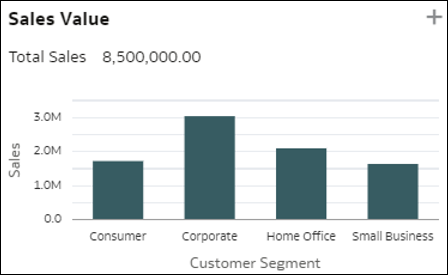
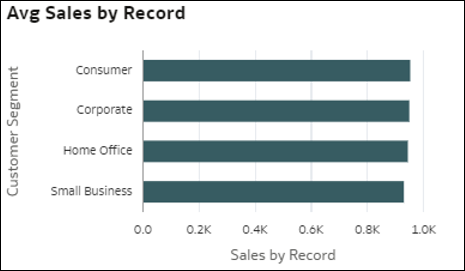
- Rozkłady wymiaru - te wizualizacje agregują wartość miary dla różnych elementów wymiaru w danych. Pozwala to uzyskać szybki wgląd w rozkład wybranej miary w danym wymiarze. Tą miarą może być miara ze zbioru danych, liczba rekordów lub średnia wartość miary na rekord.
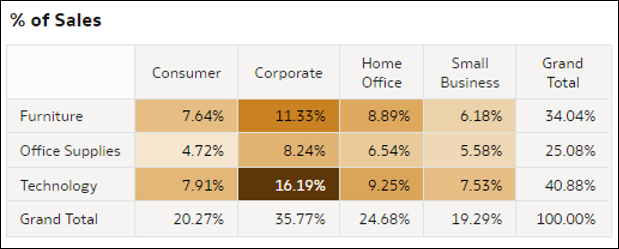
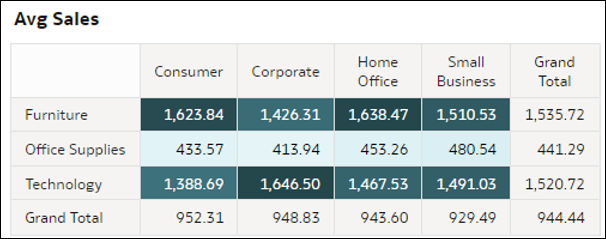
- Tabele przestawne mapy termicznej - te wizualizacje agregują wartość miary na przecięciach dwóch wymiarów w danych. Każda komórka w tabeli przestawnej reprezentuje przecięcie elementów dwóch wybranych wymiarów D2. Te wizualizacje pomagają szybko stwierdzić, gdzie znajdują się najwyższe wartości miary, gdyż są one przedstawiane za pomocą najciemniejszych komórek w tabelach. Miarami w tej wizualizacji mogą być: miara ze zbioru danych, liczba rekordów, średnia wartość metryki na rekord lub wartość procentowa reprezentująca dowolną z tych opcji (z sumą w prawym górnym rogu równą 100%).
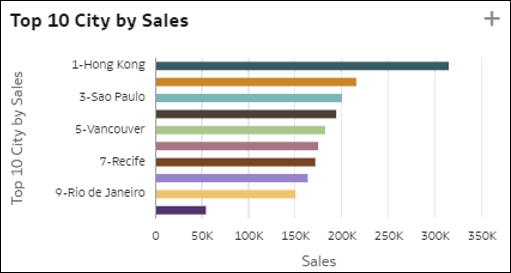
- 10 czołowych elementów - ta wizualizacja przedstawia czołowe elementy wymiaru według ich malejącej wartości dla miary w zbiorze danych. Ostatni słupek na wykresie przedstawia średnią wartość miary dla wszystkich elementów, które nie znajdują się wśród dziewięciu czołowych. Innymi słowy jest to średnia wartość M1 ze wszystkich elementów, które nie zostały zaliczone do czołowych. Stanowi to informację o tym, jak bardzo czołowe elementy odbiegają od wartości średniej z pozostałej części populacji.
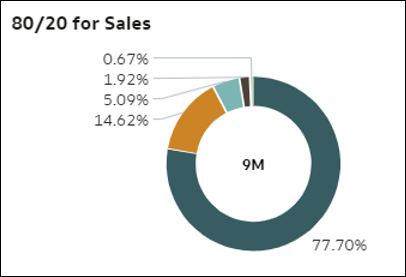
- 80/20 - ta wizualizacja pokazuje (dla danej miary), jak duża jest waga rekordów w czołowych 20% danych w odniesieniu do całego zbioru danych. Czołowe 20% jest obliczane na podstawie szczegółowych wierszy w zbiorze danych. Wykres torusowy przedstawia istotność czołowych elementów w danych dla określonej miary. Łuki na wykresie torusowym reprezentują kwintyle rekordów, czyli kolejne fragmenty po 20% rekordów, uporządkowane zgodnie z malejącą liczbą wierszy (20% czołowych elementów, potem następne 20% itd.). Wielkość łuków reprezentuje całkowitą zagregowaną wartość miary dla każdego kwintyla.
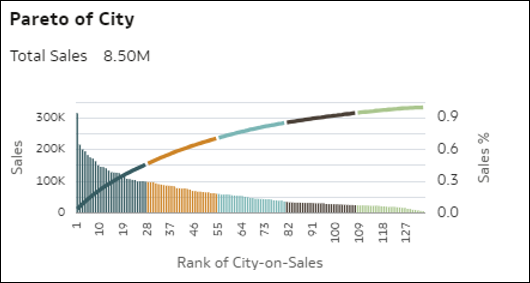
- Pareto - wizualizacja z wykresem Pareto przedstawia wszystkie elementy wymiaru (o średniej kardynalności) uporządkowane zgodnie z malejącą wartością miary. Każdy słupek reprezentuje tę miarę dla elementu, a linia reprezentuje skumulowany procent wartości miary (sumujący się do 1.0 = 100%), gdyż każdy element wymiaru jest dodawany kumulatywnie. Wykres Pareto pomaga skupić zainteresowanie na obszarach, które wykazują największą względną wartość lub częstotliwość.
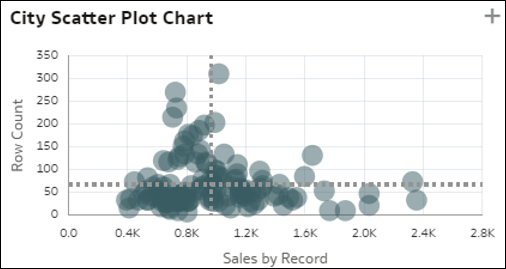
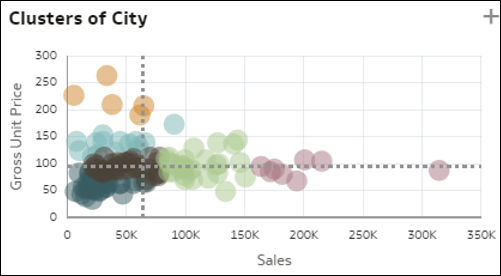
- Wykresy punktowe i klastry - wizualizacja z wykresem punktowym przedstawia wszystkie elementy wymiaru (o średniej kardynalności) na siatce, na której osiami są dwie dystynktywne miary występujące w danych. Każda miara jest wyskalowana według średniej wartości jednostkowej. Rozrzut między tymi wszystkimi rekordami i potencjalne wartości odstające są podstawą do interesujących spostrzeżeń dotyczących elementów wymiaru. Ten wykres daje szybki wgląd w to, jak bardzo te dwie miary korelują ze sobą w elementach B1 i pozwala łatwo zrozumieć, które elementy mieszczą się w którym kwadrancie. Wariant wykresu punktowego przedstawia automatyczne klastrowanie rekordów w sześć koherentnych grup.
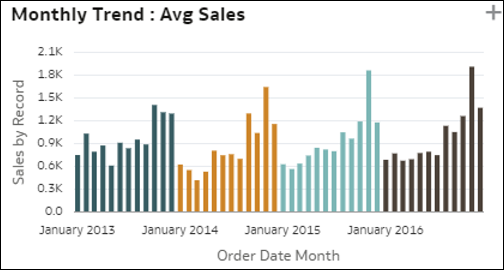
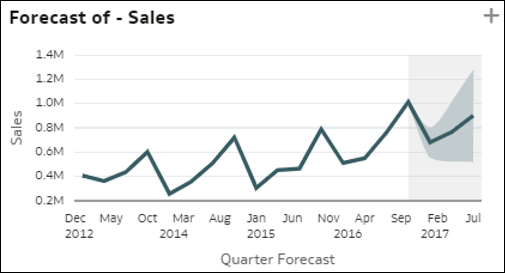
- Proste wykresy słupkowe trendów - ta wizualizacja przedstawia wykazującą trend ewolucję miary w kolumnie czasu w zbiorze danych. Może ona ujawnić interesujące wzorce trendów, takie jak wzrost lub spadek. Ta miara może być miarą ze zbioru danych, liczbą rekordów lub wartością średnią miary na rekord. To samo spostrzeżenie może być również wyświetlane z dodatkową linią prognozy po prawej stronie wykresu.
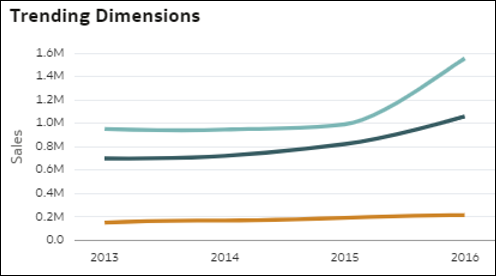
- Porównanie trendów według wymiaru - ta wizualizacja umożliwia porównanie, w jaki sposób wartość miary wykazywała trend wraz z upływem czasu dla każdego elementu wymiaru występującego w danych. Każda linia na tym wykresie reprezentuje ewolucję miary dla danego elementu wymiaru. Wzrost lub spadek wartości miary może nie być spójny we wszystkich elementach wymiaru, co może być interesującym spostrzeżeniem na temat tego, które elementy wykazują trendy inne od pozostałych.
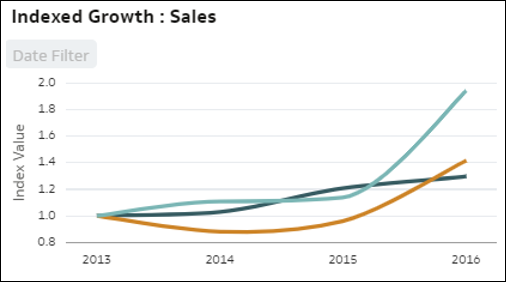
- Porównanie trendów indeksowanych - ta wizualizacja umożliwia porównanie względnego wzrostu miary w czasie dla każdego elementu kolumny wymiaru występującego w danych. Każda linia reprezentuje jeden element wymiaru, przy czym dla okresu początkowego jest ustalona bazowa wartość indeksu wynosząca 1.00. Ewolucja w czasie pokazuje wartość względną w następnych okresach w porównaniu do wartości indeksu wynoszącej 1.00 w okresie początkowym. Korzystanie z indeksowania zamiast wartości bezwzględnych pozwala na rzetelne porównanie różnych trendów, ponieważ linie przedstawiają prawdziwą względną ewolucję, co umożliwia prawidłowe wzajemne porównanie wzrostu wszystkich elementów. W przypadku analizowania wartości bezwzględnych miar zamiast ich wartości indeksowanych, rozbieżności w wartościach często uniemożliwiają prawidłowe porównanie wzrostu lub spadku. Korzystanie z indeksów pomaga zrozumieć rzeczywiste względne relacje.
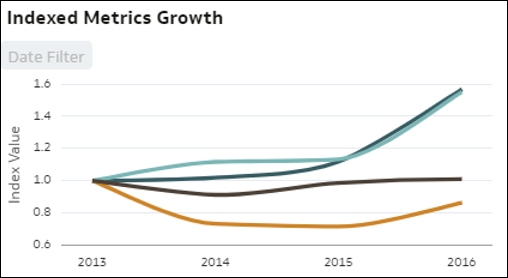
- Trendy indeksowane według miar - ta wizualizacja umożliwia porównanie względnej ewolucji w czasie dla kilku miar występujących w zbiorze danych. Ten wykres liniowy przedstawia indeksowaną wartość różnych miar w zbiorze danych w czasie, przy czym każda linia reprezentuje jedną miarę. Korzystanie z indeksowania zamiast z wartości bezwzględnych pozwala na rzetelne porównanie różnych trendów, podczas gdy bezpośrednie analizowanie wartości bezwzględnych miar często uniemożliwiałoby prawidłowe porównanie wzrostu lub spadku. Dla wszystkich miar wartość początkowa indeksu (1.00) jest ustalana na początkowy okres, a linia pokazuje względną ewolucję każdej z miar w porównaniu do jej punktu początkowego na wykresie (indeks).
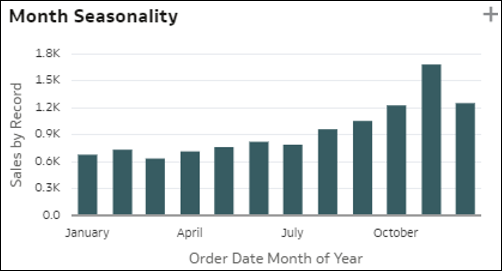
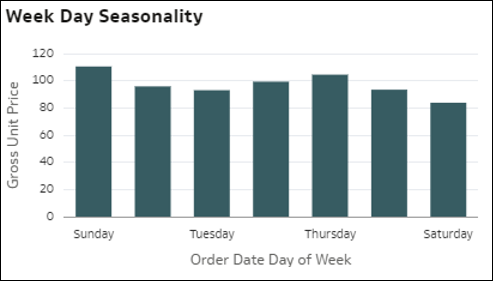
- Sezonowość - słupki w tej wizualizacji przedstawiają rozkład miary według miesiąca roku, dnia miesiąca lub dnia tygodnia dla obiektu czasu występującego w zbiorze danych. Daje to wgląd w potencjalną sezonowość wartości tego współczynnika w okresie wielu miesięcy. Wykresy sezonowości są przydatne do identyfikowania cyklicznych wzorców występujących w danych w konkretnych okresach. Może to mieć kluczowe znaczenie dla zrozumienia, w jaki sposób wartości miar zmieniają się sezonowo.
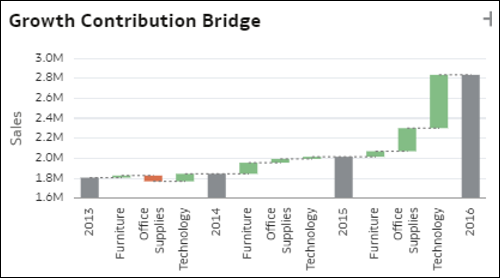
- Kaskada wpływu elementów - ten wykres kaskadowy przedstawia wkład każdego elementu wymiaru występującego w zbiorze danych w zmienność wartości miary w czasie. Pomaga to zrozumieć, które elementy miały największy wpływ na zmianę (wzrost lub spadek) w danym okresie. Każdy szary słupek na wykresie reprezentuje całkowitą wartość miary dla okresu T1. Zielone lub czerwone słupki między dwoma okresami wskazują, które elementy wzrosły lub zmalały, a zatem w jaki sposób przyczyniły się do ogólnej zmiany.
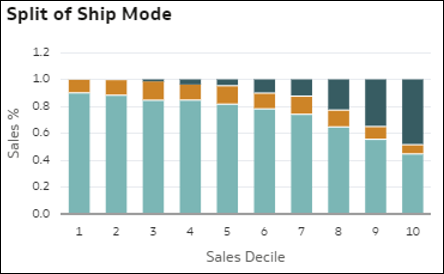
- Podział (miks) elementów wymiaru względem wartości miary - ta wizualizacja pomaga zrozumieć miks (podział) wszystkich elementów wymiaru występujących w danych wraz ze wzrostem wartości miary. Poszczególne słupki reprezentują względne wartości miary: "Decyl 1" = niska wartość miary według rekordu (pierwsze 10% rekordów), "Decyl 2" = drugie 10%, i tak do "Decyl 10" = wysoka wartość miary według rekordu. Kolor każdego ze słupków reprezentuje proporcjonalny udział (procent całości) każdego elementu wymiaru w całkowitej wartości miary dla danego decyla. Pomaga to identyfikować zmiany w strukturze miksu elementów zachodzące wraz ze zmianą wartości miary.
- Histogram miary według pojemników rekordów - ta wizualizacja pokazuje, w jaki sposób wartości jednej miary są rozdystrybuowane względem pojemników innej miary. Słupki na wykresie przedstawiają agregację miary, a każdy słupek reprezentuje jeden pojemnik dla miary: od "Pojemnik 1" = niska wartość miary według rekordu, do "Pojemnik 10" = wysoka wartość miary według rekordu.
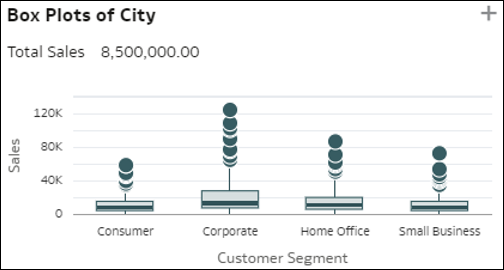
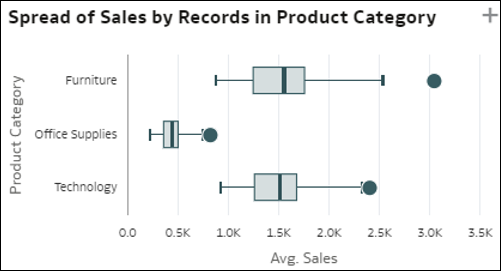
- Wykres pudełkowy elementów wymiaru - ta wizualizacja z wykresem pudełkowym umożliwia porównanie rozrzutu poszczególnych elementów w wymiarze D1 (o średniej kardynalności) występujących w danych (kropki) z wartościami miary występującej w danych, co jest przedstawiane przy użyciu poszczególnych elementów innego wymiaru D2 występującego w danych (słupki). Każdy pionowy słupek na wykresie pudełkowym reprezentuje element wymiaru D2, a każda kropka przy słupku to pojedynczy element wymiaru D1, przy czym średnia wartość jednostkowa jego miary jest pokazywana na osi y. Każdy słupek reprezentuje trzy wartości dla tego elementu wymiaru D2: wartość pierwszego kwartyla na dole słupka, wartość średnią pośrodku słupka i wartość trzeciego kwartyla na górze. Ta wizualizacja pomaga zrozumieć rozrzut rekordów w wymiarze D1 i porównać różnice w tym rozrzucie z elementami wymiaru D2.
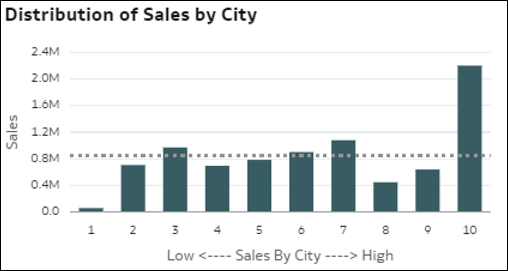
- Rozrzut wartości rekordów według wymiaru - ta wizualizacja z wykresem przedstawia dyspersję (rozrzut) w rekordach pod względem wartości miary dla każdego z elementów wymiaru (słupki). Na osi x pokazywana jest średnia wartość miary według rekordu. Kropki przy każdym ze słupków reprezentują losowe grupy granularnych rekordów ze zbioru danych. Ta wizualizacja pomaga zrozumieć, w jaki sposób rozrzut może się różnić w przypadku różnych elementów wymiaru (różniące się poziome słupki w wizualizacji).
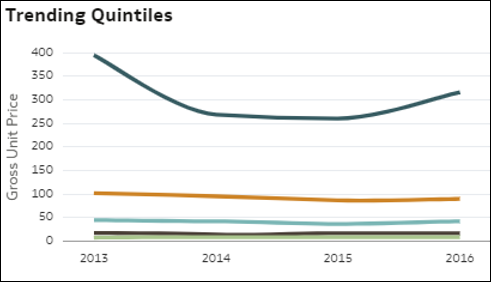
- Porównanie trendów kwintyli - ta wizualizacja umożliwia porównanie, w jaki sposób każda z 20-procentowych grup rekordów występujących w danych (posortowanych według wartości miary), od najwyższej do najniższej (kwintyle), zmieniała się wraz z upływem czasu pod względem wartości miary. Czy wzrost lub spadek był spójny w górnej i dolnej grupie? Dla której grupy w populacji trend miary jest inny? Każda linia na wykresie jest kwintylem pokazującym trend wartości M1 w czasie. Kwintyle to grupy po 20% rekordów ze zbioru danych uporządkowane zgodnie z malejącą wartością miary: rekordy z najwyższymi 20 procentami wartości, następnie z kolejnymi 20 procentami itd.