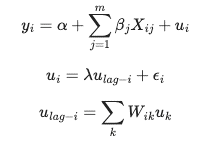Spatial Error Model

The Spatial Error Model (SEM) introduces a spatial lag in the error term of the linear equation.

By adding the spatial lag of the residual, the neighbors' errors influence the observation error. This leads to an extra parameter to be associated with the spatial lag of the error term as shown in the following formula:

Description of the illustration sem_formula.png

In the preceding formula, W is the spatial weights matrix.

The SpatialErrorRegressor class implements the spatial error model, which requires the definition of the spatial_weights_definition parameter to use it. The following table describes the main methods of the SpatialErrorRegressor class.

Method	Description
fit	Trains the SpatialErrorRegressor model from the given training data. The model includes a parameter for the spatial lag of the error term.
predict	Uses the trained parameters, including the one associated with the spatial lag of the error term, to estimate the target variable of the given data.
fit_predict	Calls the fit and predict methods sequentially with the training data.
score	Returns the R-squared statistic for the given data.

See the SpatialErrorRegressor class in Python API Reference for Oracle Spatial AI for more information.

The following example uses the block_groups SpatialDataFrame. It creates an instance of the SpatialErrorRegressor class defining the spatial_weights_definition parameter which establishes the relationship between neighboring observations. Then, it adds the model in a spatial pipeline along with a preprocessing step to standardize the data. The model is trained using a training set (X_train) and the MEDIAN_INCOME column as the target variable. Finally, it calls the predict and score methods with the test set (X_test) to estimate the values of the target variable and the model's R-Square score respectively.

from oraclesai.preprocessing import spatial_train_test_split 
from oraclesai.weights import KNNWeightsDefinition 
from oraclesai.regression import SpatialErrorRegressor 
from oraclesai.pipeline import SpatialPipeline 
from sklearn.preprocessing import StandardScaler 

# Define features
X = block_groups[["MEDIAN_INCOME", "MEAN_AGE", "HOUSE_VALUE", "INTERNET", "geometry"]] 

# Define training and test sets
X_train, X_test, _, _, _, _ = spatial_train_test_split(X, y="MEDIAN_INCOME", test_size=0.2, random_state=32) 

# Create an instance of SpatialErrorRegressor
spatial_error_model = SpatialErrorRegressor(spatial_weights_definition=KNNWeightsDefinition(k=5)) 

# Add the model in a Spatial Pipeline along with a preprocessing step
spatial_error_pipeline = SpatialPipeline([("scaler", StandardScaler()), ("spatial_error", spatial_error_model)]) 

# Train the model with MEDIAN_INCOME as the target variable
spatial_error_pipeline.fit(X_train, "MEDIAN_INCOME") 

# Print the predictions with the test set
spatial_error_predictions_test = spatial_error_pipeline.predict(X_test.drop(["MEDIAN_INCOME"])).flatten() 
print(f"\n>> predictions (X_test):\n {spatial_lag_predictions_test[:10]}") 

# Print the R-squared metric with the test set
spatial_error_r2_score = spatial_error_pipeline.score(X_test, y="MEDIAN_INCOME") 
print(f"\n>> r2_score (X_test):\n {spatial_error_r2_score}")

The program produces the following output:

>> predictions (X_test):
 [ 92285.13545208 100551.0381313   30910.61123168  45166.3218764
 177515.68764358  44088.89962954  98205.35728383  27788.19879028
  72553.17695035  24875.81828048]

>> r2_score (X_test):
 0.635646418630968

Note that printing the property summary of the trained model displays an extra lambda parameter. This parameter is associated with the spatial lag of the error term.

REGRESSION
----------
SUMMARY OF OUTPUT: MAXIMUM LIKELIHOOD SPATIAL ERROR (METHOD = FULL)
-------------------------------------------------------------------
Data set            :     unknown
Weights matrix      :     unknown
Dependent Variable  :     dep_var                Number of Observations:        2750
Mean dependent var  :  69703.4815                Number of Variables   :           4
S.D. dependent var  :  39838.5789                Degrees of Freedom    :        2746
Pseudo R-squared    :      0.6285
Sigma-square ML     :472895616.755                Log likelihood        :  -31440.423
S.E of regression   :   21746.163                Akaike info criterion :   62888.846
                                                 Schwarz criterion     :   62912.523

------------------------------------------------------------------------------------
            Variable     Coefficient       Std.Error     z-Statistic     Probability
------------------------------------------------------------------------------------
            CONSTANT    70397.9327157     855.6991730      82.2694878       0.0000000
            MEAN_AGE    4337.6721310     537.9090592       8.0639507       0.0000000
         HOUSE_VALUE    20927.8165549     706.2614165      29.6318276       0.0000000
            INTERNET    10643.3244395     580.3422845      18.3397363       0.0000000
              lambda       0.5152500       0.0215703      23.8869736       0.0000000
------------------------------------------------------------------------------------
================================ END OF REPORT =====================================